《剑指 Offer》专项突破版 - 面试题 93 : 最长斐波那契数列(C++ 实现)
题目链接:最长斐波那契数列
题目:
输入一个没有重复数字的单调递增的数组,数组中至少有 3 个数字,请问数组中最长的斐波那契数列的长度是多少?例如,如果输入的数组是 [1, 2, 3, 4, 5, 6, 7, 8],由于其中最长的斐波那契数列是 1、2、3、5、8,因此输出 5。
分析:
所谓斐波那契数列,是指数列中从第三个数字开始每个数字都等于前面两个数字之和,如数列 1、2、3、5、8、13 就是一个斐波那契数列。
可以从左至右每次从输入的数组中取出一个数字,使之和前面的若干数字组成斐波那契数列。一个数字可能和前面不同的数字组成不同的斐波那契数列。例如,输入数组 [1, 2, 3, 4, 5, 6, 7, 8],假设我们处理到数字 6,数字 6 就可以和前面的数字组成两个斐波那契数列,分别是 1、5、6 和 2、4、6。也就是说,每处理到一个数字时可能面临若干选择,需要从这些选择中找出最长的斐波那契数列。解决一个问题需要多个步骤,每一步面临若干选择,这个题目看起来适合运用回溯法。但由于这个问题没有要求列出所有的斐波那契数列,而是找出最长斐波那契数列的长度,也就是求最优解,因此可以用动态规划来解决这个问题。
分析确定状态转移方程:
应用动态规划的关键在于找出状态转移方程。将数组记为 A,A[i] 表示数组中下标为 i 的数字。对于每个 j(0 <= j < i),A[j] 都有可能是在某个斐波那契数列中 A[i] 前面的一个数字。如果存在一个 k(0 <= k < j)满足 A[k] + A[j] = A[i],那么这 3 个数字就组成了一个斐波那契数列。这个以 A[i] 为结尾、前一个数字是 A[j] 的斐波那契数列是在以 A[j] 为结尾、前一个数字是 A[k] 的序列的基础上增加一个数字 A[i],因此前者的长度是在后者的长度的基础上加 1。
例如,在数组 A = [1, 2, 3, 4, 5, 6, 7, 8] 中,A[7] 等于 8。数字 8 既可以在 1、2、3、5(结尾数字为 A[4])的基础上形成更长的斐波那契数列,也可以和数字 6(A[5])一起形成斐波那契数列 2、6、8,还可以和数字 7(A[6])一起组成斐波那契数列 1、7、8。虽然序列 2、6 和 1、7 本身都不是斐波那契数列,但在后面添加数字 8 之后就变成斐波那契数列。
由于以 A[i] 为结尾的斐波那契数列的长度依赖于它前面的数字 A[j],不同的 A[j] 能和 A[i] 形成不同的斐波那契数列,它们的长度也可能不同。因此,状态转移方程有两个参数 i 和 j,f(i, j) 表示以 A[i] 为最后一个数字、A[j] 为倒数第 2 个数字的斐波那契数列的长度。如果数组中存在一个数字 k,使 A[i] = A[j] + A[k](0 <= k < j < i),那么 f(i, j) = f(j, k) + 1,即在以 A[j] 为最后一个数字、A[k] 为倒数第 2 个数字的斐波那契数列的基础上增加一个数字 A[i],形成更长的一个数列。f(i, j) 的值可能是 2,此时虽然 A[i] 和 A[j] 这两个数字现在还不能形成一个有效的斐波那契数列,但可能会在之后增加一个新的数字使之形成长度为 3 甚至更长的斐波那契数列。
根据状态转移方程写代码:
由于状态转移方程有两个参数 i 和 j,因此需要一个二维数组来缓存 f(i, j) 的计算结果。i 对应二维数组的行号,j 对应二维数组的列号。由于 i 大于 j,因此实际上只用到了二维数组的左下角部分。如果数组的长度是 n,那么 i 的取值范围为 1 ~ n - 1,而 j 的取值范围为 0 ~ n - 2。
下表记录了计算数组 [1, 2, 3, 4, 5, 6, 7, 8] 中最长斐波那契数列的长度的过程。
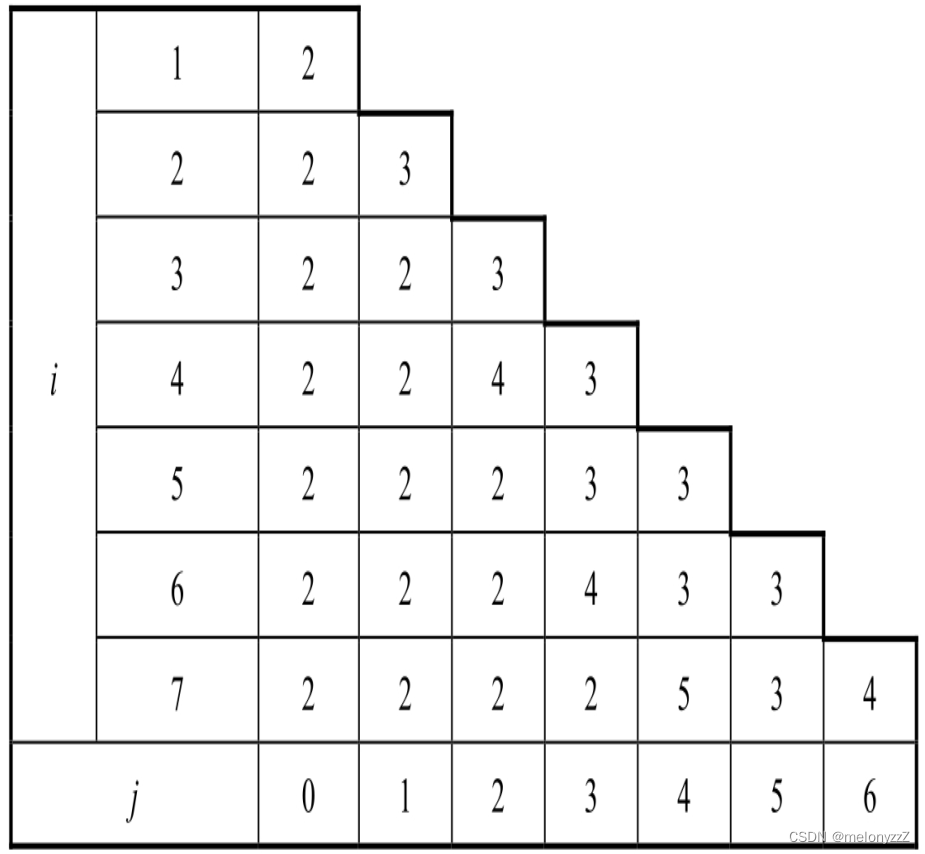
代码实现:
class Solution {
public:int lenLongestFibSubseq(vector<int>& arr) {unordered_map<int, int> numToIndex;numToIndex[arr[0]] = 0;
int n = arr.size();vector<vector<int>> dp(n, vector<int>(n - 1));int result = 0;for (int i = 1; i < n; ++i){for (int j = 0; j < i; ++j){int target = arr[i] - arr[j];if (numToIndex.count(target) && numToIndex[target] < j){int k = numToIndex[target];dp[i][j] = dp[j][k] + 1;result = max(result, dp[i][j]);}else{dp[i][j] = 2;}}numToIndex[arr[i]] = i;}return result;}
};相关文章:

《剑指 Offer》专项突破版 - 面试题 93 : 最长斐波那契数列(C++ 实现)
题目链接:最长斐波那契数列 题目: 输入一个没有重复数字的单调递增的数组,数组中至少有 3 个数字,请问数组中最长的斐波那契数列的长度是多少?例如,如果输入的数组是 [1, 2, 3, 4, 5, 6, 7, 8]࿰…...
代码随想录算法训练营第五十五天|583. 两个字符串的删除操作、72. 编辑距离
583. 两个字符串的删除操作 刷题https://leetcode.cn/problems/delete-operation-for-two-strings/description/文章讲解https://programmercarl.com/0583.%E4%B8%A4%E4%B8%AA%E5%AD%97%E7%AC%A6%E4%B8%B2%E7%9A%84%E5%88%A0%E9%99%A4%E6%93%8D%E4%BD%9C.html视频讲解https://…...

StringRedisTemplate Autowired注入为空解决
如下注入方式报空指针异常: java.lang.NullPointerException: null Autowiredprivate StringRedisTemplate redisTemplate; 解决办法:查看该类上有没有加注解,如Component等,没加的话加上。 还有一种是在工具类中使用,…...
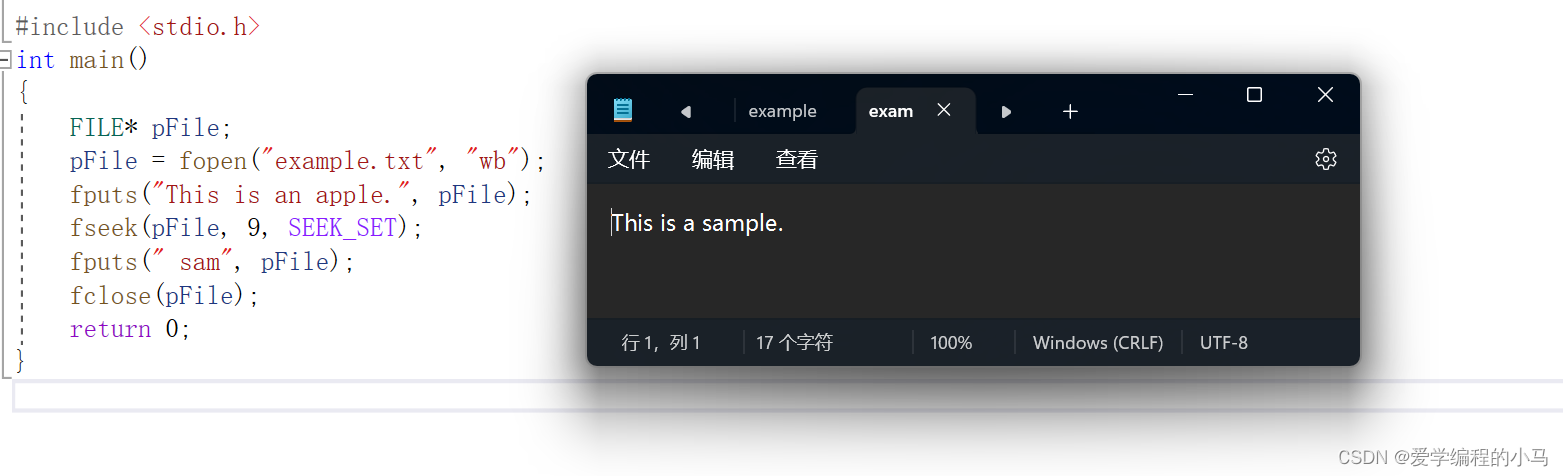
c语言:文件操作
1. 为什么使⽤⽂件? 如果没有⽂件,我们写的程序的数据是存储在电脑的内存中,如果程序退出,内存回收,数据就丢失 了,等再次运⾏程序,是看不到上次程序的数据的,如果要将数据进⾏持久…...
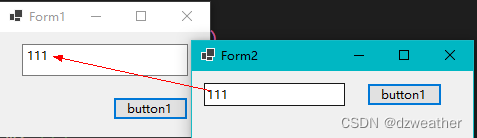
C#事件实例详解
一、什么是事件? 在C#中,事件(event)是一种特殊的类成员,它允许类或对象通知其他类或对象发生了某些事情。 从语法上看,事件的声明类似于字段,但它们在功能和行为上有一些重要的区别。 从技术角度来说,事件实际上是一个封装了事件订阅和取消订阅功能的委托字段。…...
零基础机器学习(3)之机器学习的一般过程
文章目录 一、机器学习一般过程1.数据获取2.特征提取3.数据预处理①去除唯一属性②缺失值处理A. 均值插补法B. 同类均值插补法 ③重复值处理④异常值⑤数据定量化 4.数据标准化①min-max标准化(归一化)②z-score标准化(规范化) 5.…...

用java做一个双色球彩票系统
代码如下: import java.util.Random; public class HelloWorld{public static void main(String[] args){//1、生成中奖号码 int[] arrcreateNumber();for (int i 0;i<arr.length;i) {System.out.print(arr[i]" ");}}public static int[] createNu…...
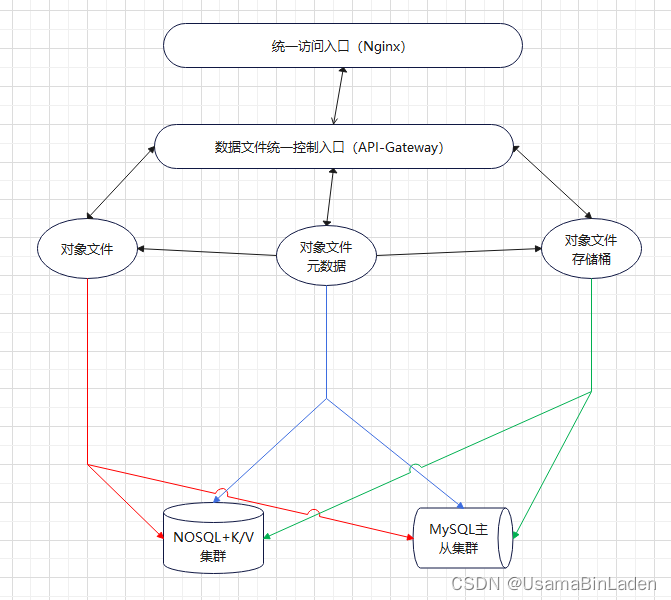
某对象存储元数据集群改造流水账
软件产品:某厂商提供的不便具名的对象存储产品,核心底层技术源自HDFS和Amazon S3,元数据集群采用了基于MongoDB的NOSQL数据库产品和MySQL数据库产品相结合。 该产品的元数据逻辑示意图如下: 业务集群现状:当前第3期建…...
——filter、foearch、for in 、for of 、for的区别以及返回值)
前端理论总结(js)——filter、foearch、for in 、for of 、for的区别以及返回值
Filter: 用途:用于筛选数组中符合条件的元素,返回一个新数组。 返回值:返回一个新数组,包含经过筛选的元素。 Foreach: 用途:遍历数组中的每个元素,执行回调函数。 返回值&#x…...
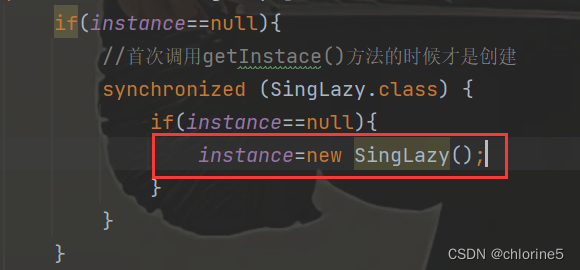
【JavaEE初阶系列】——多线程案例一——单例模式 (“饿汉模式“和“懒汉模式“以及解决线程安全问题)
目录 🚩单例模式 🎈饿汉模式 🎈懒汉模式 ❗线程安全问题 📝加锁 📝执行效率提高 📝指令重排序 🍭总结 单例模式,非常经典的设计模式,也是一个重要的学科&#x…...
革新水库大坝监测:传统软件与云平台之比较
在水库大坝的监测管理领域,传统监测软件虽然曾发挥了重要作用,但在多方面显示出了其局限性。传统解决方案通常伴随着高昂的运维成本,需要大量的硬件支持和人员维护,且软件整合和升级困难,限制了其灵活性和扩展性。 点击…...
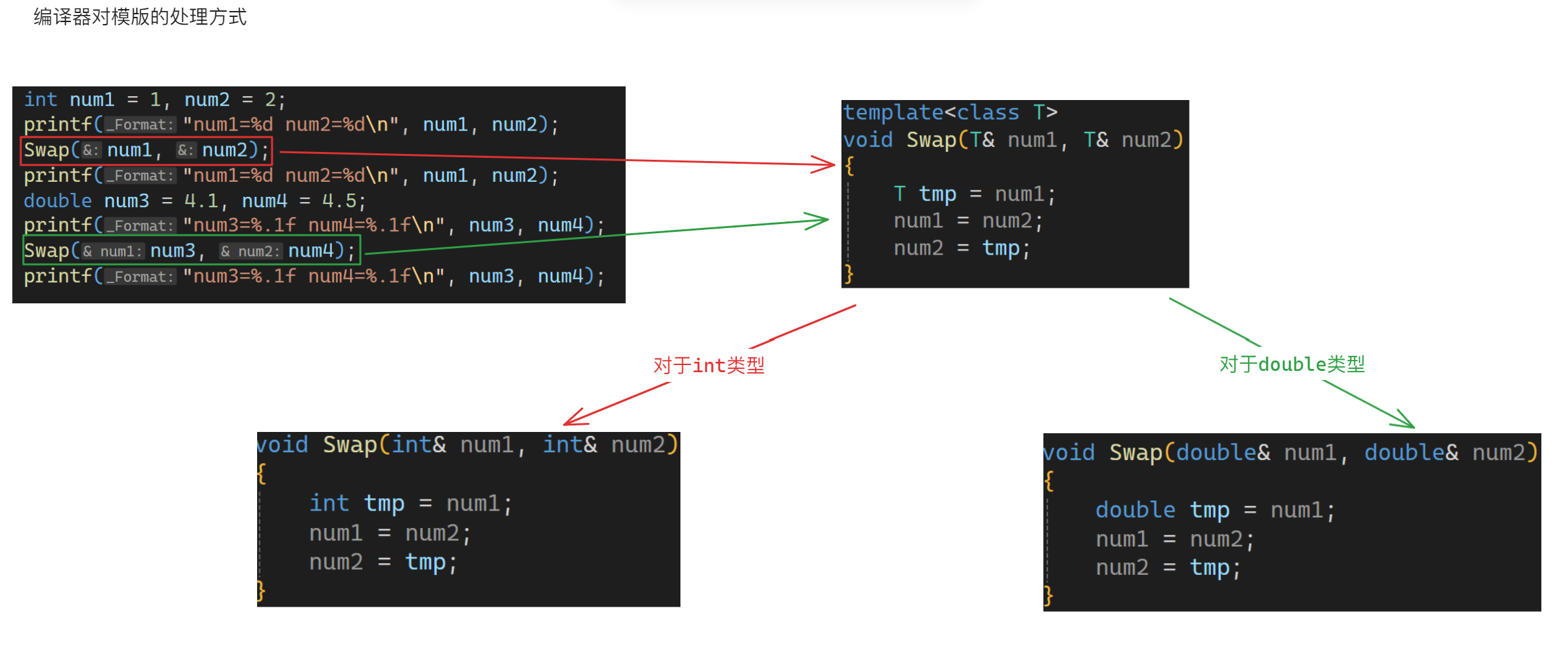
C++模版(基础)
目录 C泛型编程思想 C模版 模版介绍 模版使用 函数模版 函数模版基础语法 函数模版原理 函数模版实例化 模版参数匹配规则 类模版 类模版基础语法 C泛型编程思想 泛型编程:编写与类型无关的通用代码,是代码复用的一种手段。 模板是泛型编程…...
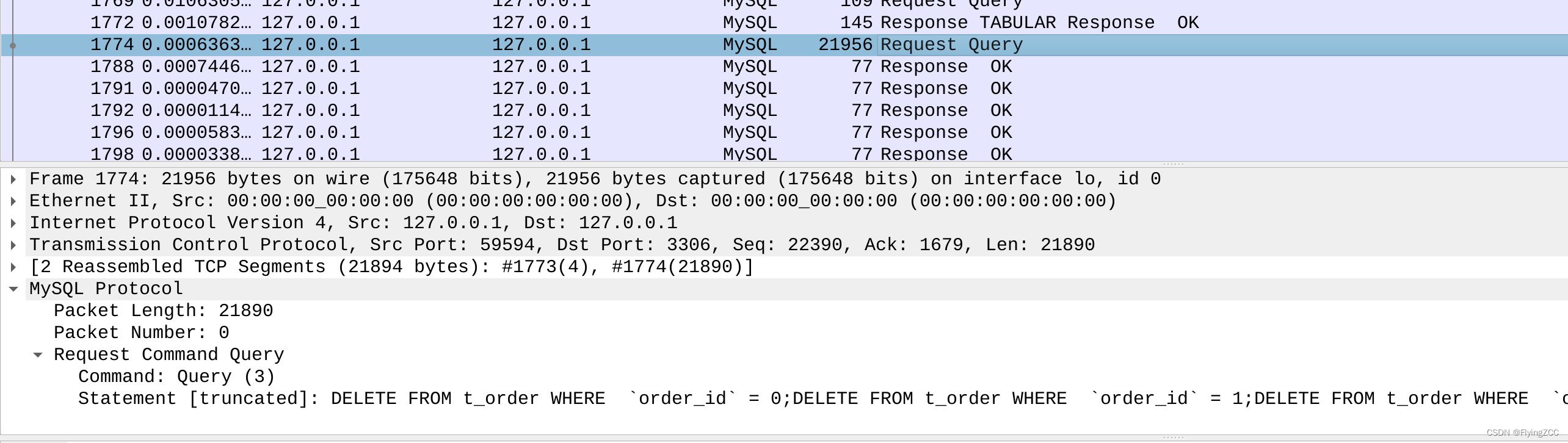
MySQL驱动Add Batch优化实现
MySQL 驱动 Add Batch 优化实现 MySQL 驱动会在 JDBC URL 添加 rewriteBatchedStatements 参数时,对 batch 操作进行优化。本文测试各种参数组合的行为,并结合驱动代码简单分析。 batch参数组合行为 useServerPrepStmts 参数 PreparedStatement psmt…...
手撕算法-数组中的第K个最大元素
描述 分析 使用小根堆,堆元素控制在k个,遍历数组构建堆,最后堆顶就是第K个最大的元素。 代码 class Solution {public int findKthLargest(int[] nums, int k) {// 小根堆PriorityQueue<Integer> queue new PriorityQueue<>…...

【vue】computed和watch的区别和应用场景
Computed 和 Watch 是 Vue.js 中用于监视数据变化的两个不同特性,它们各自有不同的应用场景和功能。 Computed: 计算属性(Computed properties)用于声明基于其他数据属性的计算值。它具有缓存功能,只有在依赖的数…...

ARM.day8
1.自己设置温度湿度阈值,当温度过高时,打开风扇,蜂鸣器报警 2.当湿度比较高时,打开LED1灯,蜂鸣器报警 main.c #include "si7006.h" #include "CH1.h" #include "led.h" // 延时函数in…...

SpringCloud Gateway工作流程
Spring Cloud Gateway的工作流程 具体的流程: 用户发送请求到网关 请求断言,用户请求到达网关后,由Gateway Handler Mapping(网关处理器映射)进行Predicates(断言),看一下哪一个符合…...

西井科技与安通控股签署战略合作协议 共创大物流全新生态
2024年3月21日,西井科技与安通控股在“上海硅巷”新象限空间正式签署战略合作框架协议。双方基于此前在集装箱物流的成功实践与资源优势,积极拓展在AI数字化产品、新能源自动驾驶解决方案和多场景应用,以及绿色物流链等领域的深度探索、强强联…...
)
CCCorelib 点云RANSAC拟合球体(CloudCompare内置算法库)
文章目录 一、简介二、实现代码三、实现效果参考资料一、简介 RANSAC是一种随机参数估计算法。RANSAC从样本中随机抽选出一个样本子集,使用最小方差估计算法对这个子集计算模型参数,然后计算所有样本与该模型的偏差,再使用一个预先设定好的阈值与偏差比较,当偏差小于阈值时…...
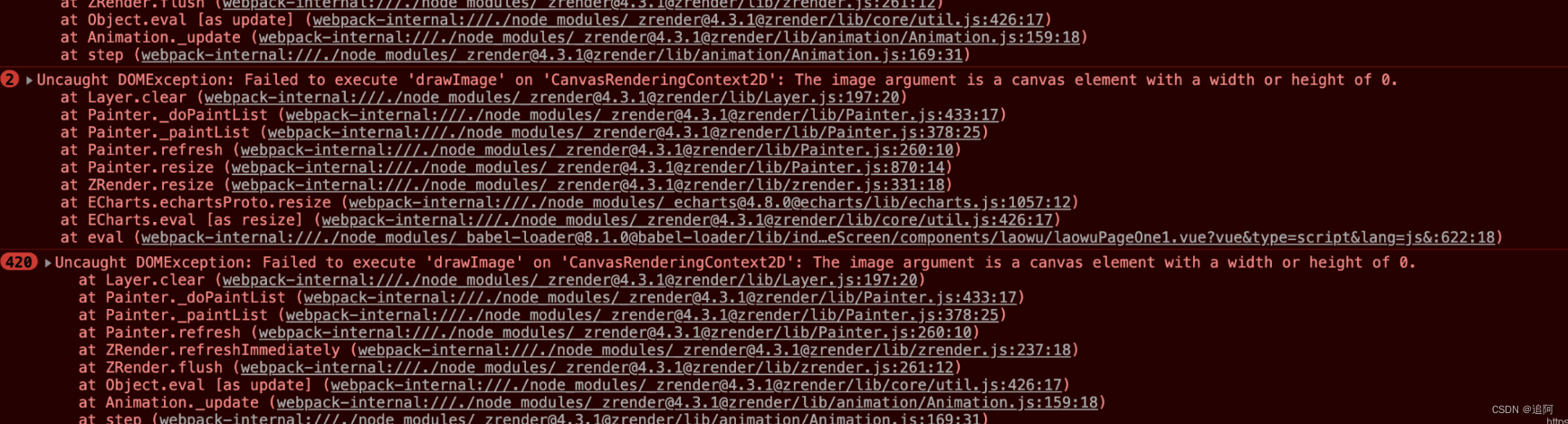
map china not exists. the geojson of the map must be provided.
map china not exists. the geojson of the map must be provided. 场景:引入echarts地图报错map china not exists. the geojson of the map must be provided. 原因: echarts版本过高,ECharts 之前提供下载的矢量地图数据来自第三方&…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...

ui框架-文件列表展示
ui框架-文件列表展示 介绍 UI框架的文件列表展示组件,可以展示文件夹,支持列表展示和图标展示模式。组件提供了丰富的功能和可配置选项,适用于文件管理、文件上传等场景。 功能特性 支持列表模式和网格模式的切换展示支持文件和文件夹的层…...
