代码随想录刷题笔记 Day 58 | 判断子序列 No.392 | 不同的子序列 No.115
文章目录
- Day 58
- 01. 判断子序列(No. 392)
- <1> 题目
- <2> 题解
- <3> 代码
- 02. 不同的子序列(No. 115)
- <1> 题目
- <2> 题解
- <3> 代码
Day 58
01. 判断子序列(No. 392)
题目链接
代码随想录题解
<1> 题目
给定字符串 s 和 t ,判断 s 是否为 t 的子序列。
字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,"ace"是"abcde"的一个子序列,而"aec"不是)。
进阶:如果有大量输入的 S,称作 S1, S2, … , Sk 其中 k >= 10亿,你需要依次检查它们是否为 T 的子序列。在这种情况下,你会怎样改变代码?
致谢:特别感谢 @pbrother 添加此问题并且创建所有测试用例。
示例 1:
输入:s = “abc”, t = “ahbgdc”
输出:true
示例 2:
输入:s = “axc”, t = “ahbgdc”
输出:false
提示:
0 <= s.length <= 1000 <= t.length <= 10^4- 两个字符串都只由小写字符组成。
<2> 题解
如果仅考虑动态规划解法的话,本题是昨天的 最长公共子序列 的简化版本。
子序列的定义为:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
**s 是否是 t 的公共子序列,其实也就代表了 t 和 s 的最长公共子序列是否是 s。**所以本题的动态规划解法就是求得它们两个最长公共子序列的长度,然后判断长度是否等于 s 的长度即可;剩下的步骤和求最长公共子序列的方法就完全相同了。
1. 状态
既然是求最长的公共子序列,那就涉及到 长度,可以分解成如下的子问题:
s 的前一个元素和 t 第一个元素组成的最长公共子序列是多少?
s 的前两个元素和 t 第一个元素组成的最长公共子序列是多少?
s 的前三个元素和 t 第一个元素组成的最长公共子序列是多少?
。。。。。。
一直推到到 s 的前 s.length() 个元素和 t 的前 t.length() 个元素的最长公共子序列的长度为多少。
那这个状态能否转移呢?s 的前 m 个元素和 t 的前 n 个元素的公共子序列的长度,是可以通过 m - 1 和 n - 1 组成的公共子序列的长度推出的。
2. dp 数组的含义
dp 数组设定为一个二维数组 dp[i][j] 表示 s 的钱 i - 1 个元素和 t 的前 j - 1 个元素构成的最长公共子序列的大小。
使用这种后移一位的方式可以减少初始化的复杂程度。
3. 递推公式
对于 s 的第 i 个元素和 t 的第 j 个元素有两种情况:
- 它们是相等的,所以它们可以作为构成子序列的元素存在
- 它们不相等,在这个 长度范围 内需要被剔除
如果它们相等,那
dp[i][j] = dp[i - 1][j - 1] + 1
如果它们不相等,那就是延续前面的子序列在如下三个中取最大:
dp[i - 1][j]dp[i - 1][j - 1]dp[i][j - 1]
但因为第二种情况被包含了,所以仅对前两个情况取值即可,也就是
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
4. 初始化
本题中,下层的推导依赖的是左上角的值,所以只需要初始化第一行和第一列即可。
而本题的第一行代表 s 的第 0 个元素(从 1 开始,0 没有意义)和 t 的最长公共子序列,为 0
第一列代表着 t 的第 0 个元素和 s 的最长公共子序列,也是 0
所以均初始化为 0 即可,也就是不需要初始化。
<3> 代码
class Solution {public boolean isSubsequence(String s, String t) {int m = 0;int n = 0;while (m < s.length() && n < t.length()) {if (s.charAt(m) == t.charAt(n)) {m++;n++;} else {n++;}}return m == s.length();}
}
02. 不同的子序列(No. 115)
题目链接
代码随想录题解
<1> 题目
给你两个字符串 s 和 t ,统计并返回在 s 的 子序列 中 t 出现的个数,结果需要对 109 + 7 取模。
示例 1:
输入:s = “rabbbit”, t = “rabbit”
输出:3
解释:
如下所示, 有 3 种可以从 s 中得到 “rabbit” 的方案。
rabbbit
rabbbit
rabbbit
示例 2:
输入:s = “babgbag”, t = “bag”
输出:5
解释:
如下所示, 有 5 种可以从 s 中得到 “bag” 的方案。
babgbag
babgbag
babgbag
babgbag
babgbag
提示:
1 <= s.length, t.length <= 1000s和t由英文字母组成
<2> 题解
1. 状态
本题虽然是困难题,但只要选好转移的状态,解答起来就比较简单了。
本题是要查询 s 中有多少种方法可以得到 t,比如第一个案例 s = “rabbbit”, t = “rabbit”,首先来考虑如何划分这个子问题:既然我去查询 s 有多少种方法可以得到 “rabbit” 比较困难,那能否先去找方法得到 “t” 呢?在之后能否得到 “it” 呢?
好,现在其实子问题的拆分就很明确了
-
s 中得到 “t” 有多少种方法?
-
s 中得到 “it” 有多少种方法?
-
s 中得到 “bit” 有多少种方法?
-
s 中得到 “bbit” 有多少种方法?
。。。。。。
-
s 中得到 “rabbit” 有多少种方法?
这种考虑方式是从后往前去考虑的,其实也可以从前往后去转移。
那这个状态能否转移呢?
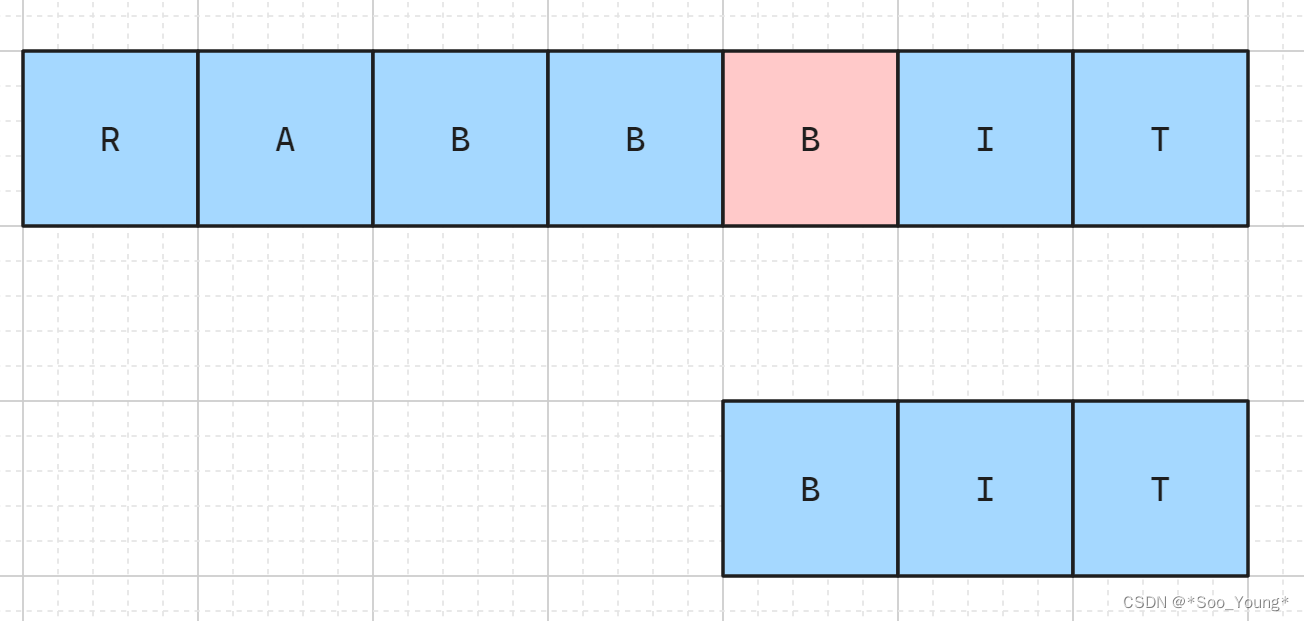
比如说现在要组成 BIT 这个序列,现在遍历到粉色的 B 了,现在,只需要知道,它后面的部分 能有几种方法组成 IT 就可以了。
2. dp 数组
本题需要一个二维的 dp 数组:
s = "rabbbit", t = "rabbit"
以上面的测试案例举例,dp[i][j] 表示目标字符串 t 从 i 到 末尾的字段在源字符串 s 从 j 到末尾的范围内有多少种构成的方式。
比如说 dp[3][0] 就是从 0 到 s.length - 1 这个范围内(“rabbbit”)构成 从 3 到 t.length - 1(“bit”)有几种方式。
3. 递推公式
还是举一个例子比较好理解:
比如说现在要计算这个节点,有多少种构成 BIT 的方式,就是要在这里寻找为 B 的节点

这时候它的前一层,也就是 dp[i + 1][j + 1] 表示从这个节点的后面开始,构成 IT 这个字段的方法
那这个节点构成 BIT 的方法就是 dp[i + 1][j + 1] 种嘛?是不对的,还需要再加上后一个节点构成 BIT 的方法,因为此时得到 BIT 的方法有如下两种:
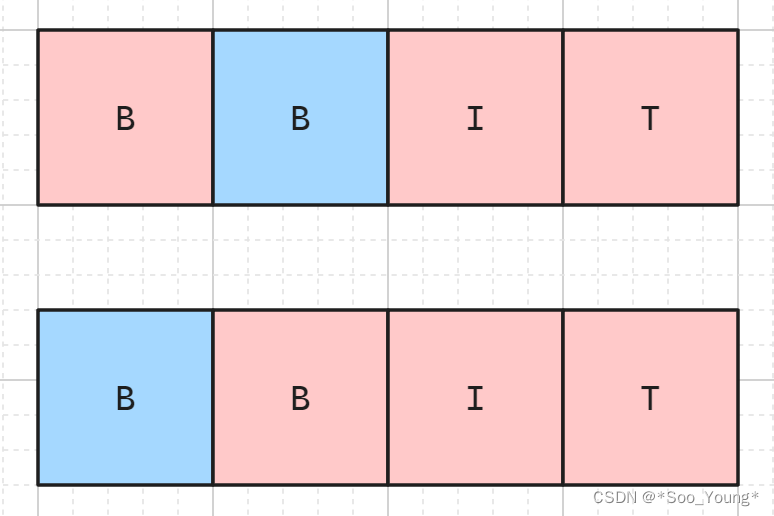
所以最终得到的递推公式就是这样:
dp[i][j] = dp[i + 1][j + 1] + dp[i][j + 1];
搞清楚递推公式的含义非常关键。
那对于不相等的情况:
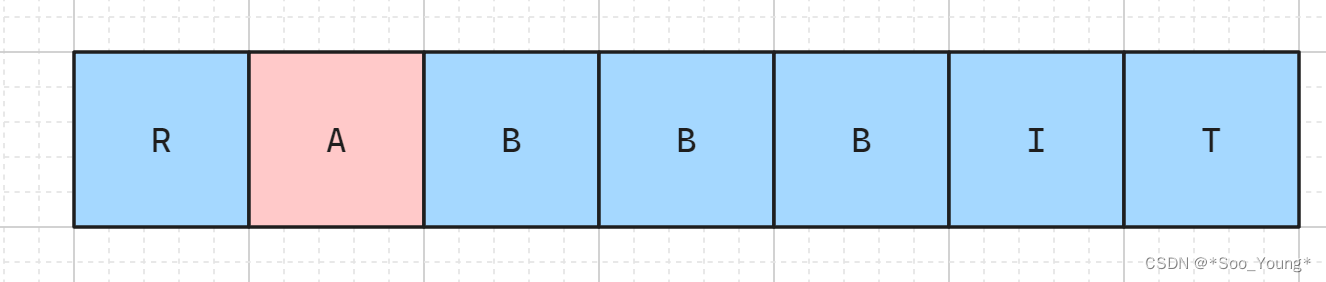
比如这里的节点 A,那此时从 A 到末尾构成 BIT 的方法就是它后面那个节点构成 BIT 的方法,得到:
dp[i][j] = dp[i][j + 1];
4. 初始化
因为本题的所有推导都是依赖第一行的,所以要先对第一行进行初始化
if (c1[c1.length - 1] == c2[c2.length - 1]) dp[c1.length - 1][c2.length - 1] = 1;for (int i = c2.length - 2; i >= 0; i--) {if (c2[i] == c1[c1.length - 1]) dp[c1.length - 1][i] = dp[c1.length - 1][i + 1] + 1;else dp[c1.length - 1][i] = dp[c1.length - 1][i + 1];}
先对最后一个元素进行特殊的处理,其他逻辑和前面的相同
<3> 代码
class Solution {public int numDistinct(String s, String t) {if (s.length() <= t.length()) {return s.equals(t) ? 1 : 0;}char[] c1 = t.toCharArray(); // 目标序列char[] c2 = s.toCharArray(); // 提供的序列int[][] dp = new int[c1.length][c2.length];if (c1[c1.length - 1] == c2[c2.length - 1]) dp[c1.length - 1][c2.length - 1] = 1;for (int i = c2.length - 2; i >= 0; i--) {if (c2[i] == c1[c1.length - 1]) dp[c1.length - 1][i] = dp[c1.length - 1][i + 1] + 1;else dp[c1.length - 1][i] = dp[c1.length - 1][i + 1];}for (int i = c1.length - 2; i >= 0; i--) {// 外层遍历要寻找的数组 c2for (int j = c2.length - 2; j >= 0; j--) {if (c1[i] == c2[j]) {dp[i][j] = dp[i + 1][j + 1] + dp[i][j + 1];} else {dp[i][j] = dp[i][j + 1];}}}return dp[0][0];}
}
相关文章:

代码随想录刷题笔记 Day 58 | 判断子序列 No.392 | 不同的子序列 No.115
文章目录 Day 5801. 判断子序列(No. 392)<1> 题目<2> 题解<3> 代码 02. 不同的子序列(No. 115)<1> 题目<2> 题解<3> 代码 Day 58 01. 判断子序列(No. 392) 题目链接…...
【C++11】thread线程库
【C11】thread线程库 目录 【C11】thread线程库thread类的简单介绍函数指针lambda表达式常用在线程中 线程函数参数join与detach利用RAII思想来自动回收线程 原子性操作库(atomic)atomic中的load函数:atomic中对变量进行原子操作的一些函数 CAS(Compare-And-Swap)无…...
实例镜像及实例创建方法)
【OpenStack】创建系统(VM)实例镜像及实例创建方法
【OpenStack】创建系统(VM)实例镜像及实例创建方法 目录 【OpenStack】创建系统(VM)实例镜像及实例创建方法创建计算镜像加载基本镜像预建镜像手动实例创建cloud-init 搭救使用 `cloud-init` 配置启动实例连接到您的新实例为实例分配 Floating IP创建SSH隧道结论推荐超级课程:…...

灵途科技助力家电智能创新
从智能家电到个护健康,科技无时无刻不在刷新我们对智慧生活的认知,我们也从未像今天这样近距离贴近智慧生活的朴素本质——传感技术。灵途科技专注光电感知技术,持续为智能家电客户提供成熟的全方位感知解决方案。步入发展第八年,…...
Flask python :logging日志功能使用
logging日志的使用 一、了解flask日志1.1、Loggers记录器1.2、Handlers 处理器1.3、Formatters 格式化器 二、使用日志2.1、官网上的一个简单的示例2.2、基本配置2.3、具体使用示例2.4、运行 三、写在最后 一、了解flask日志 日志是一种非常重要的工具,可以帮助开发…...

ethers.js:sign(签名)
Signers 在ethers中Signer是以太坊账户的抽象,可以用来签名消息和交易,如将签名的交易发送到以太坊网络以执行状态更改的操作。 npm install ethers5.4.0// 引入 import { ethers } from ethers签名 this.provider new ethers.providers.Web3Provider(…...

使用npm i进行admin依赖安装的时候出现问题
提示: npm ERR! code CERT_HAS_EXPIRED npm ERR! errno CERT_HAS_EXPIRED npm ERR! request to https://registry.npm.taobao.org/string-width failed, reason: certificate has expired 切换淘宝源到http或者更换其他国内镜像 npm config set registry http:/…...
)
【Python笔记-FastAPI】定时任务实现(APScheduler)
目录 一、常见触发器 (一) DateTrigger (二) IntervalTrigger (三) CronTrigger (四) CombinationTrigger 二、代码示例 (一) task_scheduler.py (二) client.py 三、调用说明 (一) 注册任务 (二) 查询任务 (三) 删除任务 实现功能: 定时任务注册、修改、删除、查…...

『Apisix入门篇』从零到一掌握Apache APISIX:架构解析与实战指南
📣读完这篇文章里你能收获到: 🌐 深入Apache APISIX架构: 从Nginx到OpenResty,再到etcd,一站式掌握云原生API网关的构建精髓,领略其层次化设计的魅力。 🔌 核心组件全解析ÿ…...

easyExcel大数据量导出oom
easyExcel大数据量导出 异常信息 com.alibaba.excel.exception.ExcelGenerateException: java.lang.OutOfMemoryError: GC overhead limit exceededat com.alibaba.excel.write.ExcelBuilderImpl.fill(ExcelBuilderImpl.java:84)at com.alibaba.excel.ExcelWriter.fill(Excel…...

react native上传二进制图片、视频的方法
react native获取本地图片我用的react-native-image-picker,但是它只能获取图片路径,以及base64的图片,不能获取到binary二进制形式的。 一开始我是让后端改造接口,把原本传binary的改成了base64,可是,躲得…...
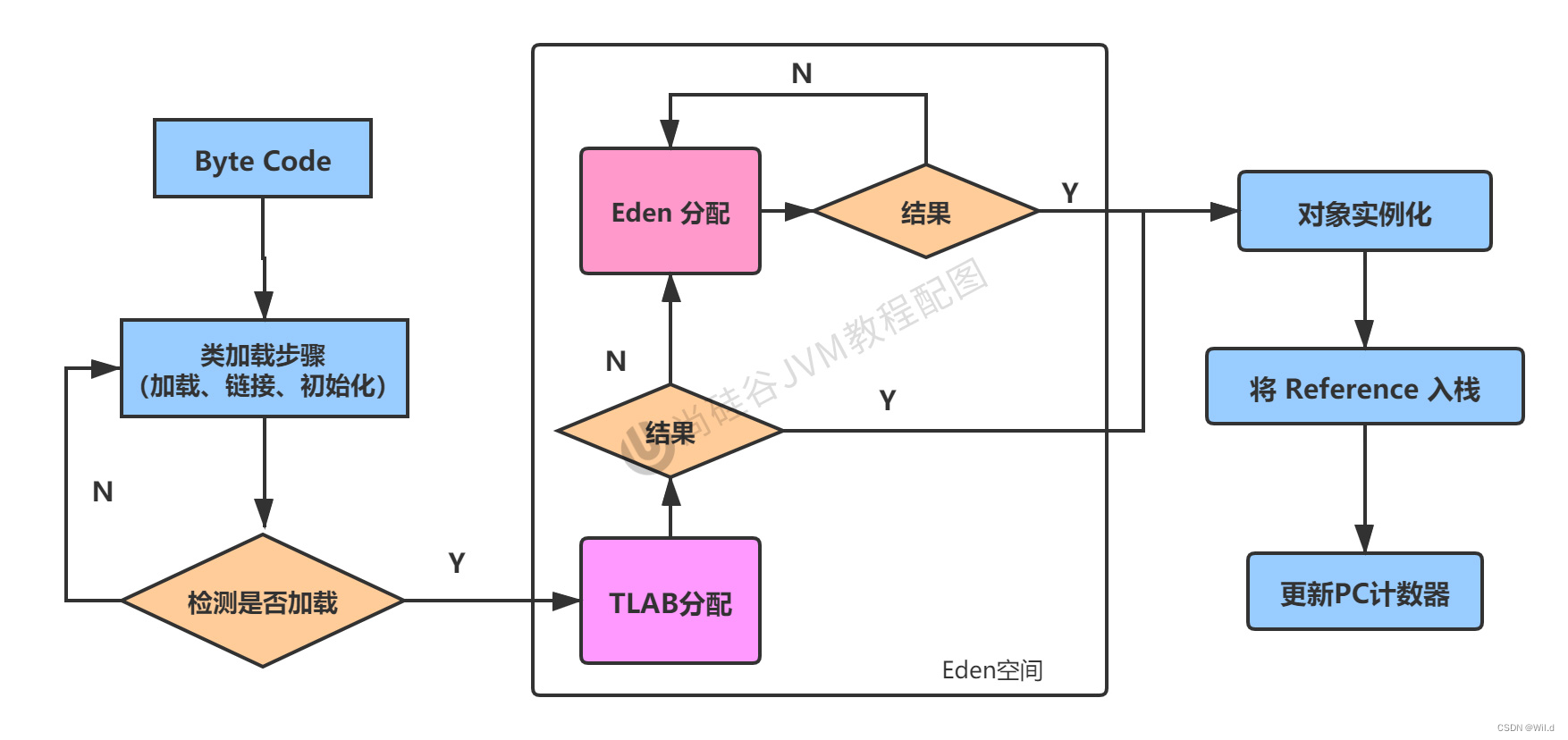
JVM之堆
堆的核心概述 一个JVM实例只存在一个堆内存,堆也是内存管理的核心区域。 Java堆区在JVM启动的时候即被创建,其空间大小也就确定了。是JVM管理的最大一块内存空间。 堆内存的大小是可以调节的。 《JVM虚拟机规范》规定,堆可以处于物理上不连…...
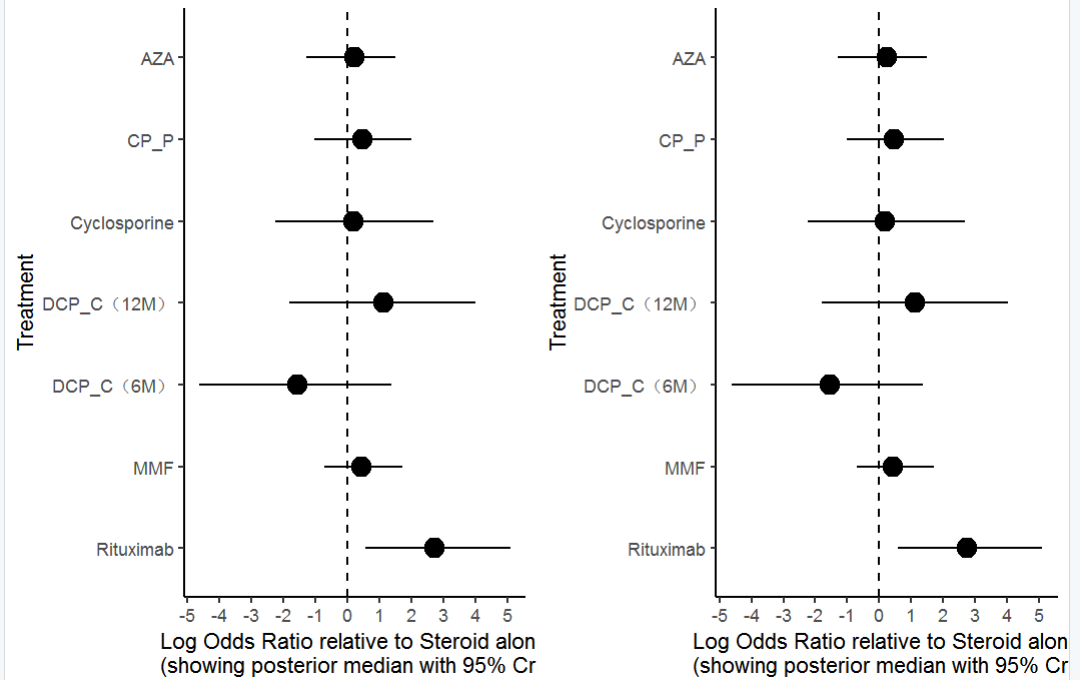
R语言实现——网状 Meta 分析
近来年,网状 Meta 分析相关研究不断涌现,此类研究不但能发表在国内各大核心期刊上,还能在SCI期刊甚至医学4大刊上看到其身影。随手在pubmed上面一搜索,就能得到一万多篇相关文献。俨然成为医学文献研究的“大杀器”! P…...
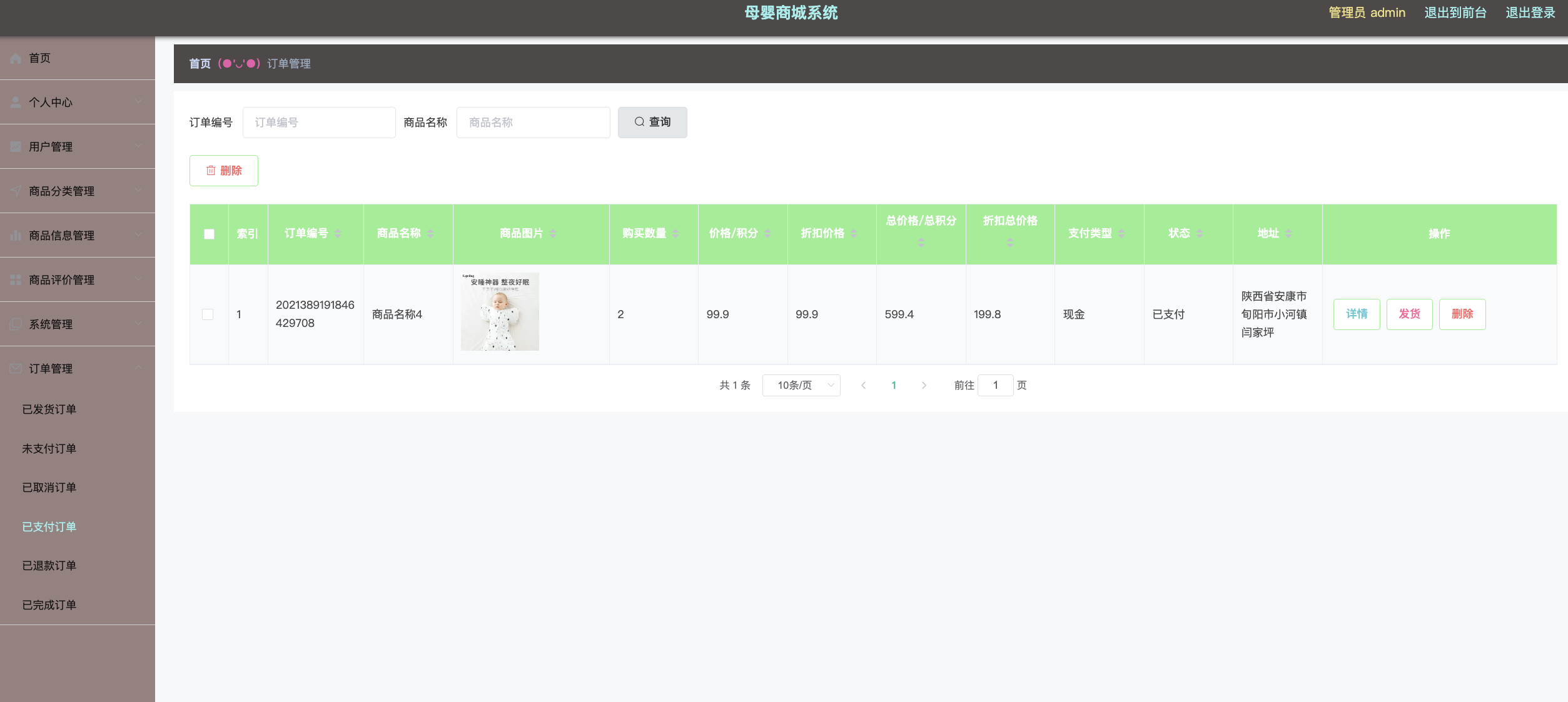
Java项目:77 springboot母婴商城
作者主页:源码空间codegym 简介:Java领域优质创作者、Java项目、学习资料、技术互助 文中获取源码 项目介绍 本课题后端使用SpringBoot Spring Cloud框架,前端采用html,JQuery,JS,DIVCSS技术进行编程&…...

【排序算法】深入解析快速排序(霍尔法三指针法挖坑法优化随机选key中位数法小区间法非递归版本)
文章目录 📝快速排序🌠霍尔法🌉三指针法🌠挖坑法✏️优化快速排序 🌠随机选key🌉三位数取中 🌠小区间选择走插入,可以减少90%左右的递归🌉 快速排序改非递归版本…...

生成微信小程序二维码
首页 -> 统计 可以通过上面二个地方配置,生成小程序的二维码,并且在推广分析里,有详细的分析数据,...

网络编程(1)写一个简单的UDP网络通信程序【回显服务器】,并且实现一个简单的翻译功能
使用 JAVA 自带的api 目录 一、回显服务器 UdpEchoServer 服务器代码 客户端代码 二、翻译功能 UdpDictServer 在UdpDictServer里重写process方法 一、回显服务器 UdpEchoServer /*** 回显服务器* 写一个简单的UDP的客户端/服务器 通信的程序* 这个程序没有啥业务逻辑&am…...
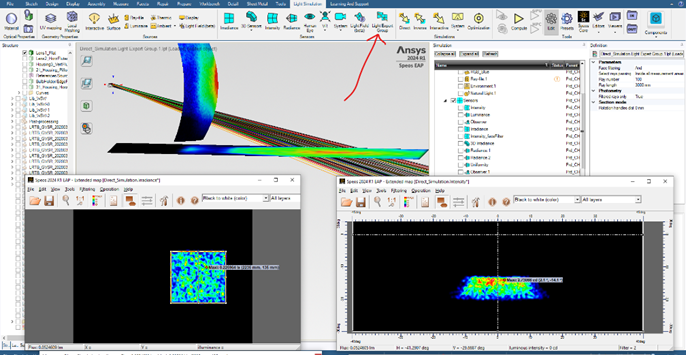
Ansys Speos | Light Expert Group探测器组使用技巧
附件下载 联系工作人员获取附件 概述 相机挡板的设计需要在光路的不同位置同步多个照度图,以尽量减少杂散光。2023R2 Speos提供了一种新的探测器,用于高阶杂散光分析,可以同时对多个探测器进行光线追迹。Light Expert工具可以即时过滤3D视…...
C#学习笔记3:Windows窗口计时器
今日继续我的C#学习之路,今日学习自己制作一个Windows窗口计时器程序: 文章提供源码解释、步骤操作、整体项目工程下载 完成后的效果大致如下:(可选择秒数,有进度条,开始计时按钮等) …...

C语言与sqlite3入门
c语言与sqlite3入门 1 sqlite3数据类型2 sqlite3指令3 sqlite3的sql语法3.1 创建表create3.2 删除表drop3.3 插入数据insert into3.4 查询select from3.5 where子句3.6 修改数据update3.7 删除数据delete3.8 排序Order By3.9 分组GROUP BY3.10 约束 4 c语言执行sqlite34.1 下载…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...
