Vue动态粒子特效插件(背景线条吸附动画)
目录
效果图:
一、安装:
二、引入 main.js 文件:
三、使用:
四、属性说明:
效果图:

一、安装:
npm install vue-particles --save二、引入 main.js 文件:
import VueParticles from 'vue-particles'
Vue.use(VueParticles)三、使用:
<vue-particlesclass="login-background"color="#409EFF":particleOpacity="0.7":particlesNumber="60"shapeType="circle":particleSize="6"linesColor="#409EFF":linesWidth="1":lineLinked="true":lineOpacity="0.4":linesDistance="150":moveSpeed="3":hoverEffect="true"hoverMode="grab":clickEffect="true"clickMode="push"></vue-particles>
.login-background {//可设置背景图 铺满屏background: linear-gradient(-180deg, #dceaf2 0%, #ffffff 100%);width: 100%;height: 100%;position: absolute;
}四、属性说明:
| 属性 | 类型 | 说明 |
| color | String | 粒子颜色(默认:#dedede) |
| particleOpacity | Number | 粒子透明度(默认:0.7) |
| particlesNumber | Number | 粒子数量(默认:80) |
| shapeType | String | 粒子外观类型(默认:circle,全部:circle,edge,triangle,polygon,star) |
| particleSize | Number | 单个粒子大小(默认:80) |
| linesColor | String | 线条颜色(默认:#dedede) |
| linesWidth | Number | 线条宽度(默认:1) |
| lineLinked | Boolean | 连接线是否可用(默认:true) |
| lineOpacity | Number | 线条透明度(默认:0.4) |
| linesDistance | Number | 线条距离(默认:150) |
| moveSpeed | Number | 粒子运动速度(默认:3) |
| hoverEffect | Boolean | 是否有hover特效(默认:true) |
| hoverMode | String | hover模式类型(grab,repulse,bubble) |
| clickEffect | Boolean | 是否有click特效(默认:true) |
| clickMode | String | click模式类型(push,remove,repulse,bubble) |
相关文章:

Vue动态粒子特效插件(背景线条吸附动画)
目录 效果图: 一、安装: 二、引入 main.js 文件: 三、使用: 四、属性说明: 效果图: 一、安装: npm install vue-particles --save 二、引入 main.js 文件: import VueParticles…...

【Java 类】002-类、属性、方法、代码块
【Java 类】002-类、属性、方法、代码块 文章目录【Java 类】002-类、属性、方法、代码块一、类1、类与对象2、类的作用3、创建与使用类类结构创建类调用类运行结果4、Java 类的执行过程5、封装、继承、多态、抽象类、内部类、接口、枚举、记录、注解等二、属性1、概述2、类型3…...

Ubuntu Linux 编译安装的基本步骤
文章目录1 基本步骤若报错: No such file or directory2 解压 tar.bz2文件参考:1 基本步骤 解压: tar -zxvf file.tar.gz 进入解压后的文件夹: cd file 源码编译安装 ./configure # ./configmakesudo make install 若报错&…...
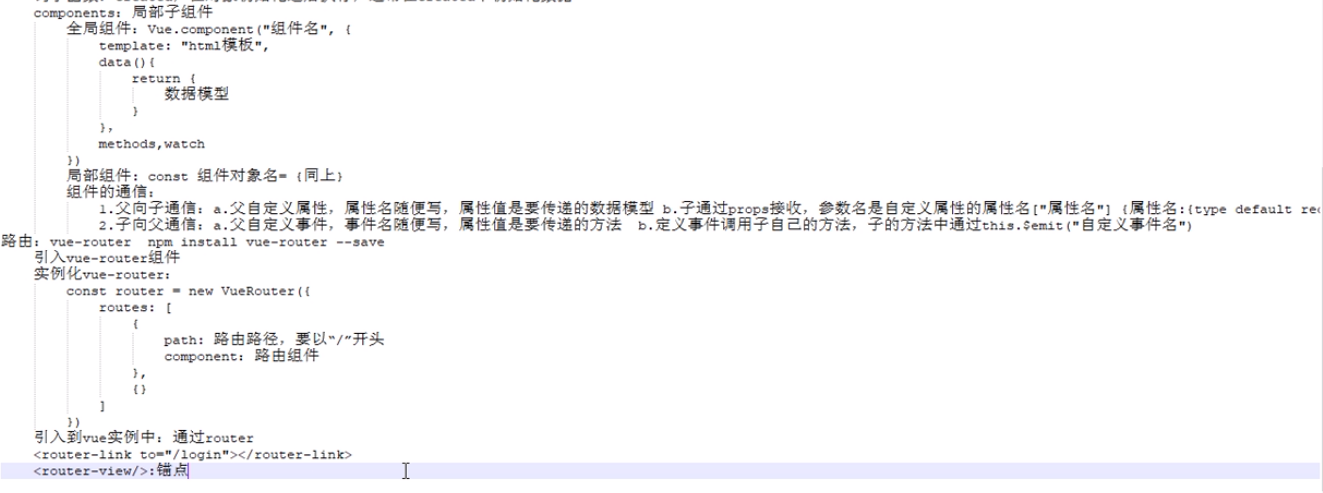
day59反刍笔记
1.本地环境安装vue后,没有vue.js文件,只有vue.cjs.js文件, 引用后也无法正常使用,看npm install vue后的文件夹中没有vue.js文件_找不到vue.js_一枝风的博客-CSDN博客 老哥的博客后得到启发,将原本的命令由࿱…...

【阅读笔记】你不知道的Javascript--强制类型转换4
目录强制类型转换基本概念JSONboolean强转归纳其他知识点被诟病的安全使用隐式强转法则抽象关系比较语法表达式变动强制类型转换 基本概念 类型转换发生在静态类型语言的编译阶段; 强制类型转换则发生在动态类型语言的运行时(runtime) JSON…...
)
华为OD机试真题Python实现【有效子字符串】真题+解题思路+代码(20222023)
有效子字符串 题目 输入两个字符串S和L,都只包含小写字母, S长度 <= 100,L长度 <= 500000, 判断S是否是L的有效子字符串, 判定规则:S中的每个字符在L中都能找到(可以不连续) 且S在L中字符的前后顺序与S中顺序要保持一致 例如: S="ace"是L="abcd…...
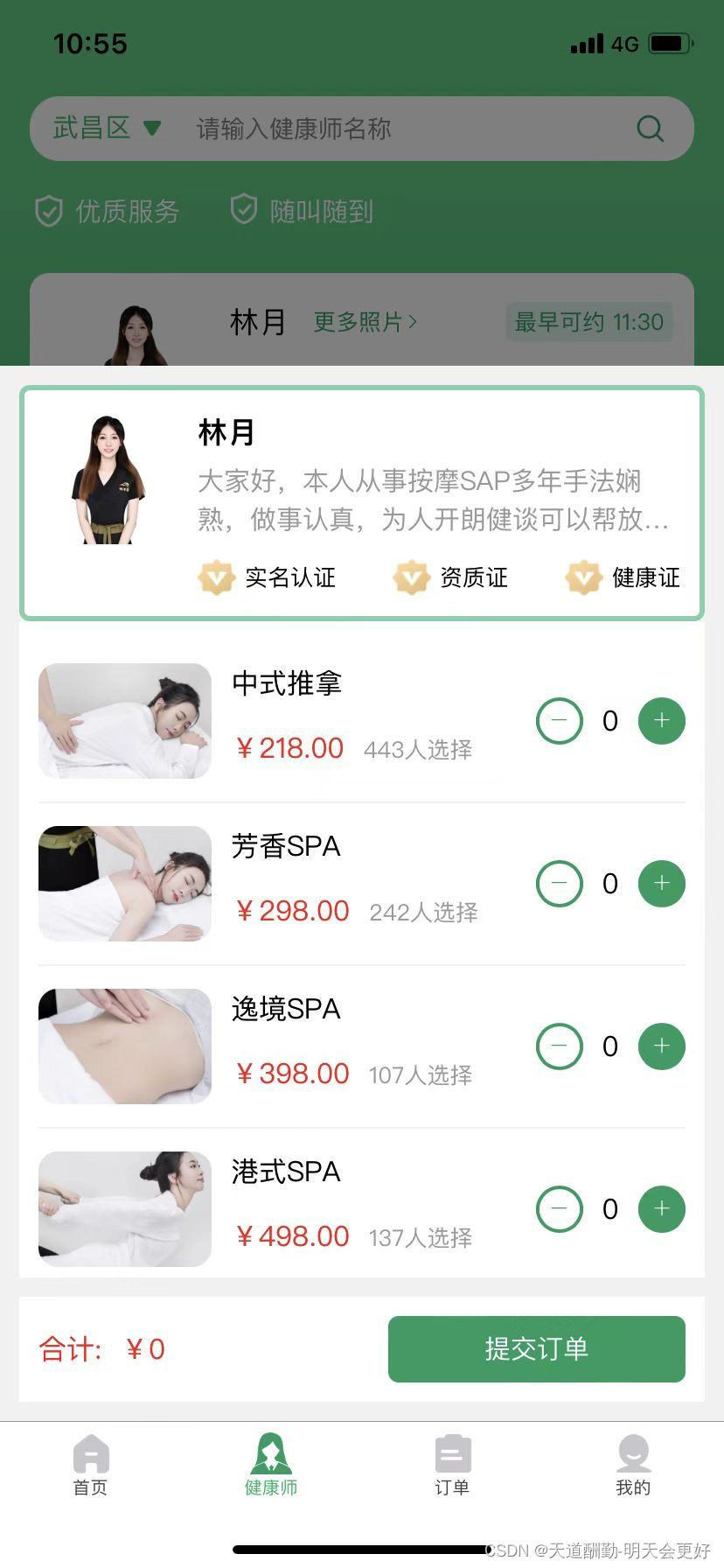
上门按摩预约APP源码-东郊到家源码(开发,PHP,平台搭建)
一、什么是上门按摩预约APP源码? 上门按摩预约APP源码是一款家政服务类型的APP,可以帮忙用户在家就能享受按摩的服务。APP源码分两端,一端是用户端,另外一端是技师端。采用的技术,前端是安卓IOS,后端是PHP&…...
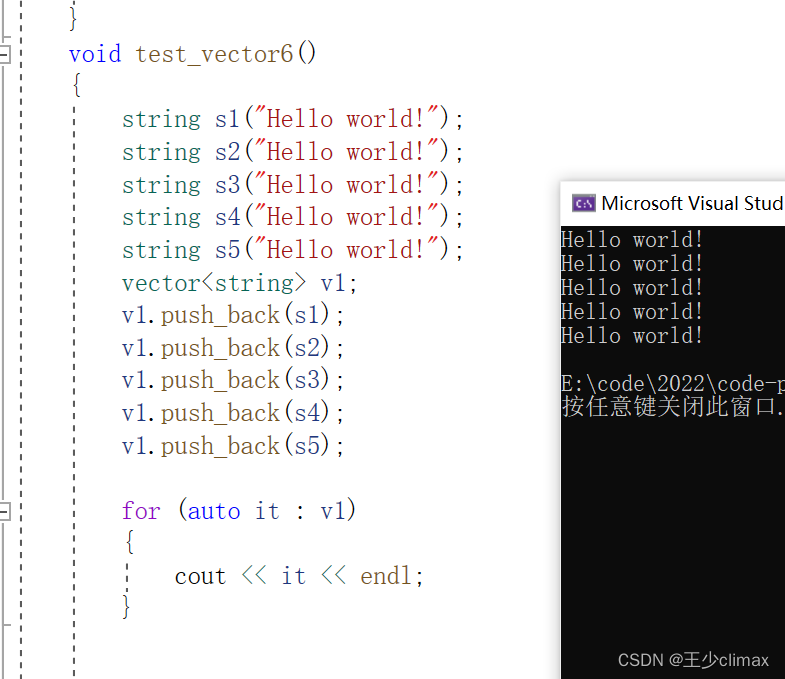
STL讲解——模拟实现vector
STL讲解——模拟实现vector vector深度剖析 在STL源码中,发现vector定义的并不是 start、size、capacity,而是start、finish、end_of_storage. 这样就可以得到size()和capacity()。 sizefinish-start capacityend_of_storage-start 扩容可能是本地扩容也…...

各种经典排序算法介绍及实现源码
一,冒泡排序(Bubble Sort) 排序算法是程序员必须了解和熟悉的一类算法,排序算法有很多种,基础的如:冒泡、插入、选择、快速、归并、计数、基数和桶排序等。 冒泡排序只会操作相邻的两个数据。每次冒泡操作都会对相邻的两个元素进行比较,看是否满足大小关系要求,如果不…...

历史大讲堂:这是真·图形化 苹果系统历史回顾(上)
众所周知,米国有个非常牛掰的公司叫苹果,想必大家对这个logo不陌生吧。 目前已发布的苹果产品有iPhone、iPad、iPod等等,简直花样繁多,而且各种功能很好用,我的手机就是一部苹果iPhone X。 等一下,似乎扯远…...
今天女神节,用python画个贺卡送给母亲吧
今天女神节,你给女神妈妈准备了什么祝福呢?如果还没有,那么画个贺卡送给她吧,在你眼里,她是一个什么样的人呢? 是"可爱",“温柔”,“美丽”,“漂亮”…...
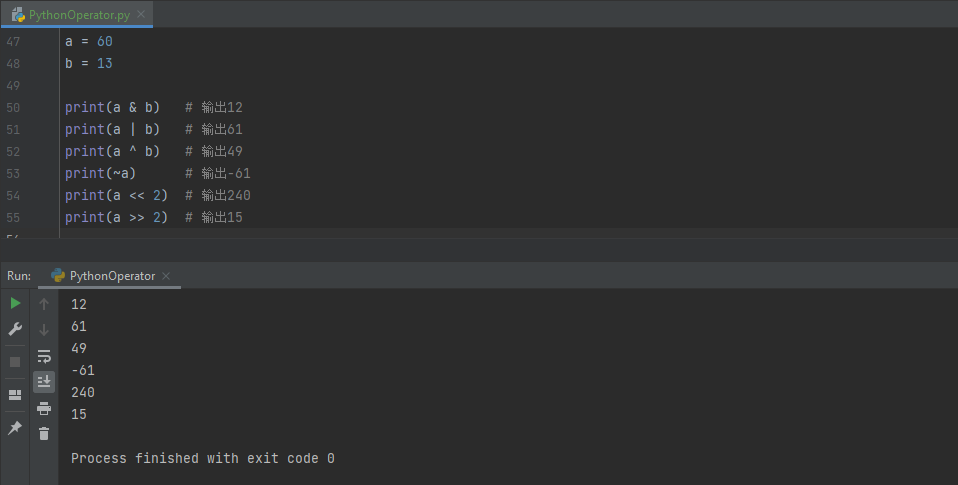
【编程基础之Python】11、Python中的表达式
【编程基础之Python】11、Python中的表达式Python中的表达式表达式与运算符算术表达式赋值表达式比较表达式逻辑表达式位运算表达式总结Python中的表达式 在Python中,表达式是由操作数、运算符和函数调用等组成的语法结构,可以进行各种数学运算、逻辑判…...
)
华为OD机试真题Python实现【乱序整数序列两数之和绝对值最小】真题+解题思路+代码(20222023)
乱序整数序列两数之和绝对值最小 题目 给定一个随机的整数数组(可能存在正整数和负整数)nums, 请你在该数组中找出两个数,其和的绝对值(|nums[x]+nums[y]|)为最小值 并返回这两个数(按从小到大返回)以及绝对值。 每种输入只会对应一个答案。但是,数组中同一个元素不能使用两…...
(python))
字符串转换整数 (atoi)(python)
链接: https://leetcode.cn/problems/string-to-integer-atoi 题目描述: 请你来实现一个 myAtoi(string s) 函数,使其能将字符串转换成一个 32 位有符号整数(类似 C/C 中的 atoi 函数)。 函数 myAtoi(string s) 的算法…...

洛谷 P1115 最大子段和
题目链接:P1115 最大子段和 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 题目描述 给出一个长度为 n 的序列 a,选出其中连续且非空的一段使得这段和最大。 输入格式 第一行是一个整数,表示序列的长度 n。 第二行有 n 个整数ÿ…...
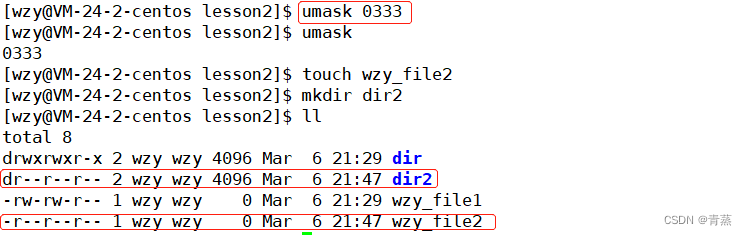
【Linux】-- 权限和Shell运行原理
目录 Shell的运行原理 用户切换 su - / su sudo 权限 chmod chown chgrp 八进制方法修改文件属性 目录权限 粘滞位 umask 自定义默认权限 Shell的运行原理 广义上,Linux发行版 Linux内核 外壳程序 Linux 从广义上来理解它是一个操作系统 而从狭义上…...
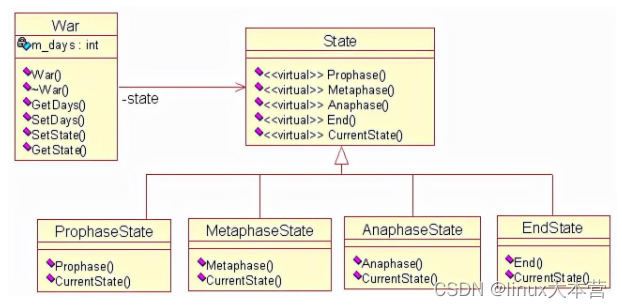
C++各类设计模式及实现详解
软件领域中的设计模式为开发人员提供了一种使用专家设计经验的有效途径。设计模式中运用了面向对象编程语言的重要特性:封装、继承、多态,真正领悟设计模式的精髓是可能一个漫长的过程,需要大量实践经验的积累。最近看设计模式的书࿰…...
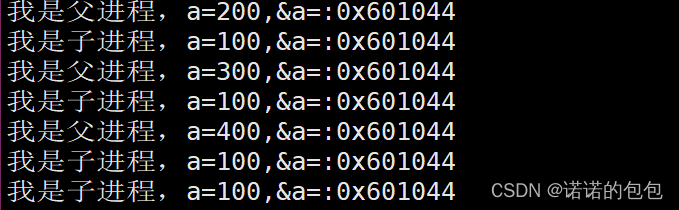
【Linux】进程理解与学习(Ⅰ)
环境:centos7.6,腾讯云服务器Linux文章都放在了专栏:【Linux】欢迎支持订阅🌹相关文章推荐:【Linux】冯.诺依曼体系结构与操作系统进程概念什么是进程?进程是什么?我们打开任务管理器可以看到有…...

认识代码之前,请先认识你自己 |《编程人生》
这是我的湛庐课程《给技术人的职场突围课》 (链接) 的一部分。 这篇文章也是 IT 女神征文活动 的一部分。 《编程人生》是一本优秀程序员的采访集,里面记录了15位世界级编程大师的故事。 我在 发刊词 里面说过,在这个书单课里&am…...

react学习笔记-5:react路由
react旧版本路由 旧版本的路由是按照组件的方式来写的 编写router/index.tsx文件 import App from "../App" import Home from "../views/Home" import About from "../views/About" import { BrowserRouter,Routes,Route } from "react…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...
