【更新中】Leetcode中遇到的最短路径算法
dijsktra算法模板:
def dijkstra(x):#x表示出发点dis=[inf]*n #dis记录从x出发到各个点的最短距离,初始化为infdis[x]=0 #源点到自己的距离为0vis=[False]*n #检查各个点是否访问过for _ in range(n-1): #检查除了源点的其他n-1个点,更新disnode=-1 #开始假设不知道谁是离源点最近的点for j in range(n):#循环查找谁是离源点最近的那个点if not vis[j] and (node==-1 or dis[j]<dis[node]):node=jfor j in range(n):#对node的邻居点进行松弛处理dis[j]=min(dis[j],dis[node]+g[node][j])vis[node]=True #对node点标记为已访问743. 网络延迟时间
因为本题的节点是从1到n,所以最后把dis数组中的第一个忽略掉(dis[1:])
然后就是经典的dijkstra最短路径算法,套用模板即可。
class Solution:def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:g=[[inf]*(n+1) for _ in range(n+1)]for x,y,w in times:g[x][y]=wdis=[inf]*(n+1)dis[k]=0vis=[False]*(n+1)for _ in range(n):x=-1for i in range(1,n+1):if not vis[i] and (x==-1 or dis[i]<dis[x]):x=ifor i in range(1,n+1):dis[i]=min(dis[i],dis[x]+g[x][i])vis[x]=Trueans=max(dis[1:])return ans if ans!=inf else -12642. 设计可以求最短路径的图类
又是dijkstra最短路径算法,这里需要判断一下能否到达终点的问题:
class Graph:def __init__(self, n: int, edges: List[List[int]]):self.n=nself.g=[[float("INF")]*n for _ in range(self.n)]for x,y,cost in edges:self.g[x][y]=costdef addEdge(self, edge: List[int]) -> None:self.g[edge[0]][edge[1]]=edge[2]def shortestPath(self, node1: int, node2: int) -> int:n=len(self.g)dis=[float('INF')]*ndis[node1]=0vis=[False]*nwhile 1:x=-1for i,(b,d) in enumerate(zip(vis,dis)):if not b and (x<0 or d<dis[x]):x=iif x<0 or dis[x]==float('INF'):return -1if x==node2:return dis[x]vis[x]=Truefor y,w in enumerate(self.g[x]):if dis[x]+w<dis[y]:dis[y]=dis[x]+w# Your Graph object will be instantiated and called as such:
# obj = Graph(n, edges)
# obj.addEdge(edge)
# param_2 = obj.shortestPath(node1,node2)1334. 阈值距离内邻居最少的城市
枚举每个点作为出发点,算法返回小于等于阈值的数目即可。
因为题目要求返回数量最少且编号最大的点,所以从n-1到0遍历即可。
class Solution:def findTheCity(self, n: int, edges: List[List[int]], distanceThreshold: int) -> int:g=[[inf]*n for _ in range(n)]for x,y,w in edges:g[x][y]=wg[y][x]=w#枚举每个点作为出发点,做dijkstra算法def dijkstra(x):dis=[inf]*ndis[x]=0vis=[False]*nfor _ in range(n-1):node=-1for j in range(n):if not vis[j] and (node==-1 or dis[j]<dis[node]):node=jfor j in range(n):dis[j]=min(dis[j],dis[node]+g[node][j])vis[node]=Truereturn sum(d<=distanceThreshold for d in dis)ans,cnt=n,inf for i in range(n-1,-1,-1):if dijkstra(i)<cnt:cnt=dijkstra(i)ans=ireturn ans相关文章:

【更新中】Leetcode中遇到的最短路径算法
dijsktra算法模板: def dijkstra(x):#x表示出发点dis[inf]*n #dis记录从x出发到各个点的最短距离,初始化为infdis[x]0 #源点到自己的距离为0vis[False]*n #检查各个点是否访问过for _ in range(n-1): #检查除了源点的其他n-1个点,更新dis…...

Git学习笔记之基础
本笔记是阅读《git pro》所写,仅供参考。 《git pro》网址https://git-scm.com/book/en/v2 git官网 https://git-scm.com/ 一、git起步 1.1、检查配置信息 git config --list查看所有的配置以及它们所在的文件 git config --list --show-origin可能有重复的变量名…...

STCubeIDE 编译bootloader
头文件重复引用解决办法。 参考:STM32CubeIDE IAP原理讲解,及UART双APP交替升级IAP实现-CSDN博客 移植到Air32时,RAM的大小(无论boot程序还是app 程序) 尽量不动,如果动了会影响最终的 APP 跳转 flash 大小可以随意修改…...

Python学习:函数
函数定义 在Python中,函数(Function)是一组用于完成特定任务或计算的语句块。定义函数可以让我们将一段代码重用多次,提高代码的可读性和可维护性。以下是定义函数的基本语法和结构: def function_name(parameters):&…...

docker run 使用 -p 命令一直显示端口被占用
解决办法 将 -p 换成 --net host 例如: docker run --name one-api -d --restart always -p 3000:3000 -e TZ=Asia/Shanghai -v /root/oneapi/data:/data justsong/one-api # 换成 docker run --name one-api -d --restart always --net...

Rust 实战练习 - 1. 输入,输出,环境变量,字符,字符串
目标: 获取程序命令行参数标准输入输出获取环境变量字符串,字符初步学习 cargo传递参数,需要加上-- use std::{env, ffi::OsString, io, io::Write};fn main() {println!("OS Env: {:?} > {:?}", env::current_dir().unwra…...
)
RuoYi-Vue-Plus(登录流程)
一、前端登录请求 登录按钮: src\views\login.vue 页面中登录片段,调用了handleLogin 方法,如下: @click.native.prevent="handleLogin" <el-button:loading="loading"size="medium"type="primary"style="width:100%;&qu…...

【数学】 【分数】 【字符串】972. 相等的有理数
本文涉及知识点 数学 分数 字符串 LeetCode972. 相等的有理数 给定两个字符串 s 和 t ,每个字符串代表一个非负有理数,只有当它们表示相同的数字时才返回 true 。字符串中可以使用括号来表示有理数的重复部分。 有理数 最多可以用三个部分来表示&…...

【4】DongshanPI-Seven 应用开发_文件IO
目录 1.文件IO1.1 文件IO分类1.2 查看系统调用IO用法 2. open 函数3. write 函数4. read 函数5 dup函数 1.文件IO 1.1 文件IO分类 在Linux系统中,一切都是“文件”:普通文件、驱动程序、网络通信等。所有的操作都是通过文件IO来操作的。 在Linux操作文…...

SEO 的未来:GPT 和 AI 如何改变关键词研究
谷歌Gemini与百度文心一言:AI训练数据的较量 介绍 想象一下,有一个工具不仅可以理解错综复杂的关键字网络,还可以预测搜索引擎查询的变化趋势。 这就是生成式预训练 Transformer (GPT) 和其他人工智能技术发挥作用的地方,以我们从…...
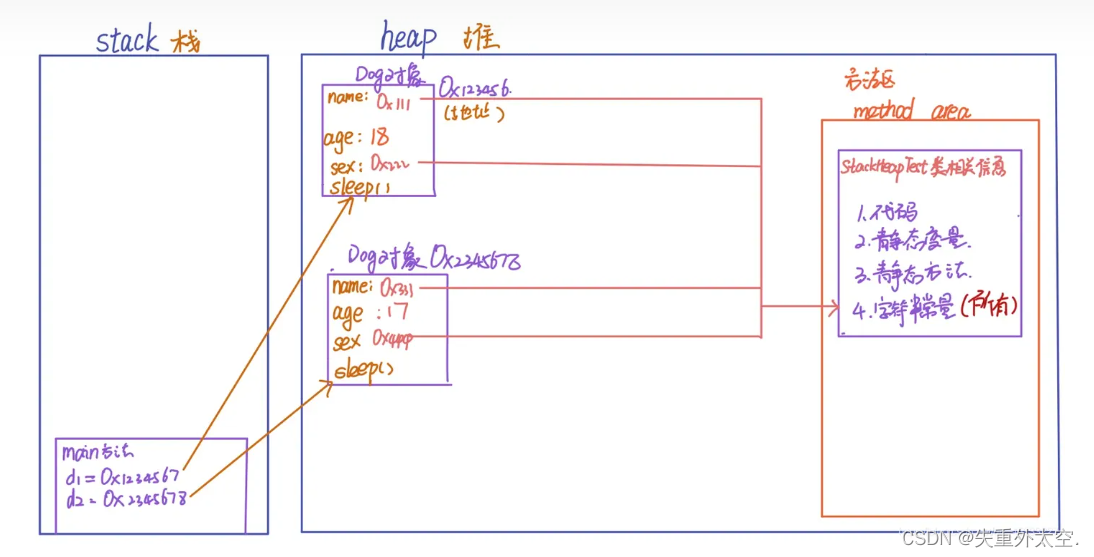
面试八股文之JAVA基础
JAVA基础 DNS、CDN?如何实现对象克隆?父子类静态代码块, 非静态代码块, 构造方法执行顺序?String s new String("abc") 创建了几个对象, 分别放到哪里?OSI网络模型七层?应用层协议?http协议和https协议区别?传输层协…...

网络连接中——长连接和短连接详解
一、TCP功能 TCP在真正开始进行数据传输之前,Server 和 Client 之间必须建立一个连接。当数据传输完成后,双方不再需要这个连接时,就可以释放这个连接。 TCP连接的建立是通过三次握手,而连接的释放是通过四次挥手。所以说,每个TCP连接的建立和释放都是需要消耗资源和时间…...
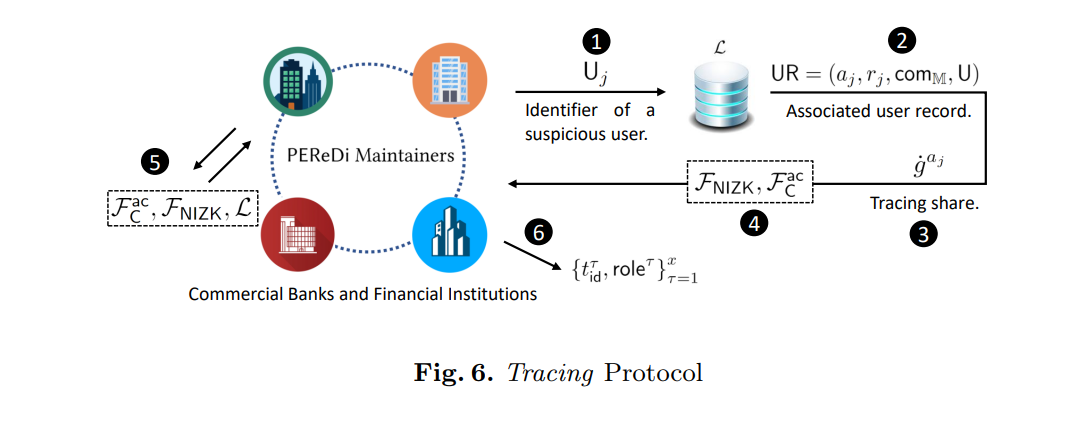
PEReDi 完全隐私的央行数字货币方案
第一个对完全隐私保护建模的方案,基于账户模型,要求交易双方都在线。 角色分类 中央银行 B B B:负责发行数字货币和货币政策,但不控制用户账户的状态,没有能力对交易的发送者或接收者进行去匿名化或披露与特定交易相…...

yolov5+pyside6+登录+用户管理目标检测可视化源码
一、软件简介 这是基于yolov5目标检测实现的源码,提供了用户登录功能界面; 用户需要输入正确的用户名和密码才可以登录。如果是超级管理员,可以修改普通用户的信息,并且在检测界面的右上角显示【管理用户】按钮。 支持图片、视频、…...

电脑如何设置个性便签 电脑个性便签分享
每次坐在电脑前,我都仿佛置身于一片信息的海洋。工作、生活、学习,方方面面的事情都需要我用心去记录。在这样一个快节奏的时代,电脑无疑成了我最得力的助手。但记事的时候,我总希望有一个既方便又有个性的工具,能让我…...
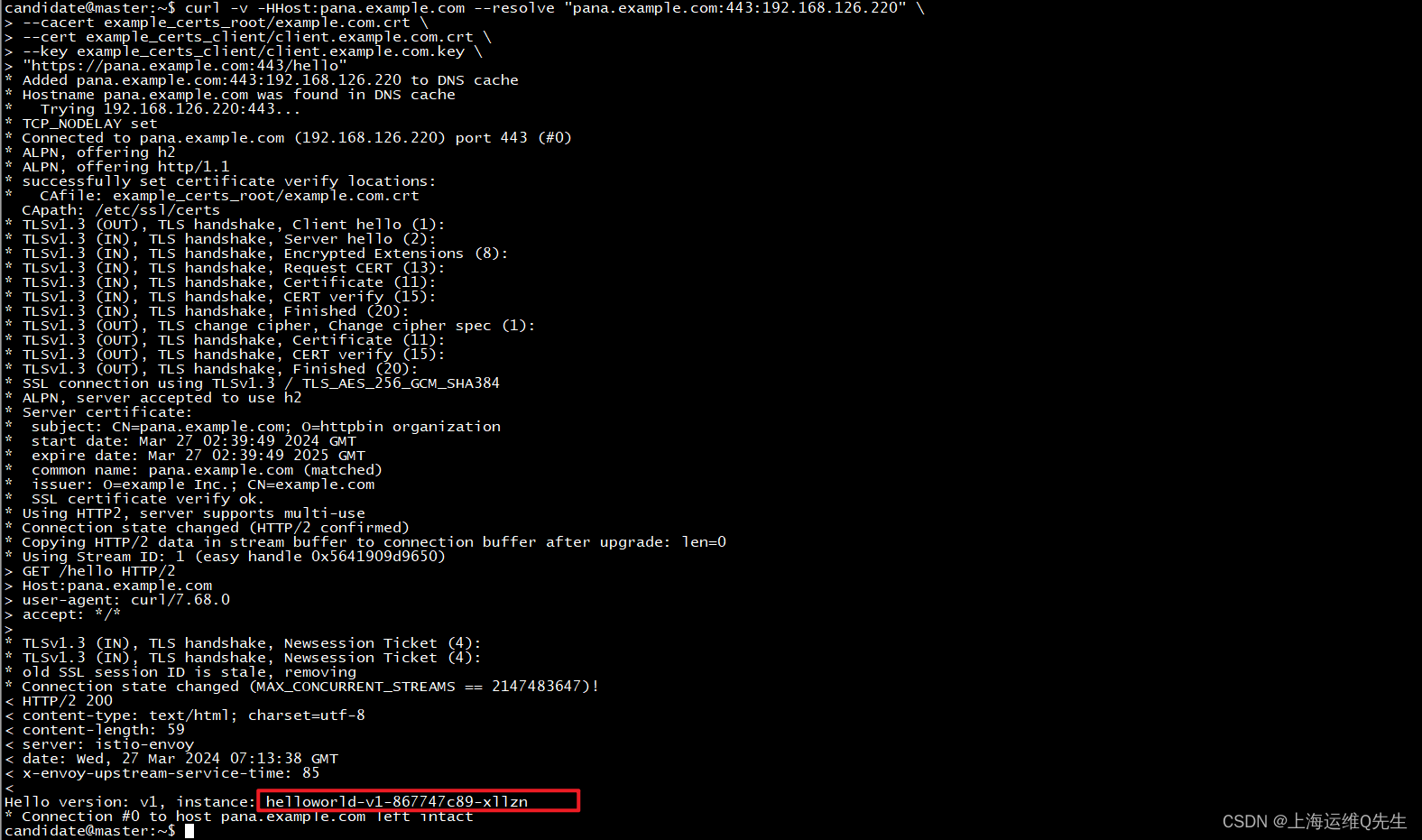
备考ICA----Istio实验12---配置双向TLS Istio Ingress Gateway实验
备考ICA----Istio实验12—配置双向TLS Istio Ingress Gateway实验 本实验部分配置延续上个Istio实验11 1. 重新配置secret 重新配置secret使其带有ca证书可以验证客户端证书是否合法 先删除原有secret,再配置新的secret # 删除原tls类型的secret kubectl -n istio-system d…...

SpringBoot 统一后端返回格式、处理全局异常
文章目录 引言I 统一标准格式1.1 定义返回标准格式1.2 定义状态码1.3 返回数据模型1.4 枚举定义1.5 Json序列化处理1.6 获取枚举字典II 处理全局异常2.1 全局异常处理器2.2 自定义异常2.3 请求数据模型III 预备知识:注解3.1 JsonInclude3.2 JsonIgnoreProperties...
C++学习基础版(一)
目录 一、C入门 1、C和C的区别 2、解读C程序 3、命名空间 4、输入输出 (1)cout输出流 (2)endl操纵符 (3)cin输入流 二、C表达式和控制语句 1、数据机构 特别:布尔类型bool 2、算数运…...

Rust 双向链表 LinkedList 和安全删除元素的方法
一、LinkedList 基本用法 在Rust中,LinkedList 是标准库中 std::collections 模块提供的一个双向链表实现。这个双向链表在每个节点中都保存了其前一个和后一个节点的引用,允许在链表的任一端进行有效的添加和移除操作。 以下是一个简单的示例…...

Android 开发中 Gradle 使用详解:构建、配置与优化技巧
文章目录 1. 基本概念2. 配置构建脚本2.1 项目级构建脚本2.2 模块级构建脚本 3. 自定义构建变体和应用 flavorDimensions4. 多模块项目4.1 创建模块4.2 配置模块依赖 5. 使用 Gradle 插件6. 使用 Gradle 命令 Gradle 是一种先进的构建工具,它被广泛应用于 Android 开…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

AxureRP-Pro-Beta-Setup_114413.exe (6.0.0.2887)
Name:3ddown Serial:FiCGEezgdGoYILo8U/2MFyCWj0jZoJc/sziRRj2/ENvtEq7w1RH97k5MWctqVHA 注册用户名:Axure 序列号:8t3Yk/zu4cX601/seX6wBZgYRVj/lkC2PICCdO4sFKCCLx8mcCnccoylVb40lP...

SQL注入篇-sqlmap的配置和使用
在之前的皮卡丘靶场第五期SQL注入的内容中我们谈到了sqlmap,但是由于很多朋友看不了解命令行格式,所以是纯手动获取数据库信息的 接下来我们就用sqlmap来进行皮卡丘靶场的sql注入学习,链接:https://wwhc.lanzoue.com/ifJY32ybh6vc…...
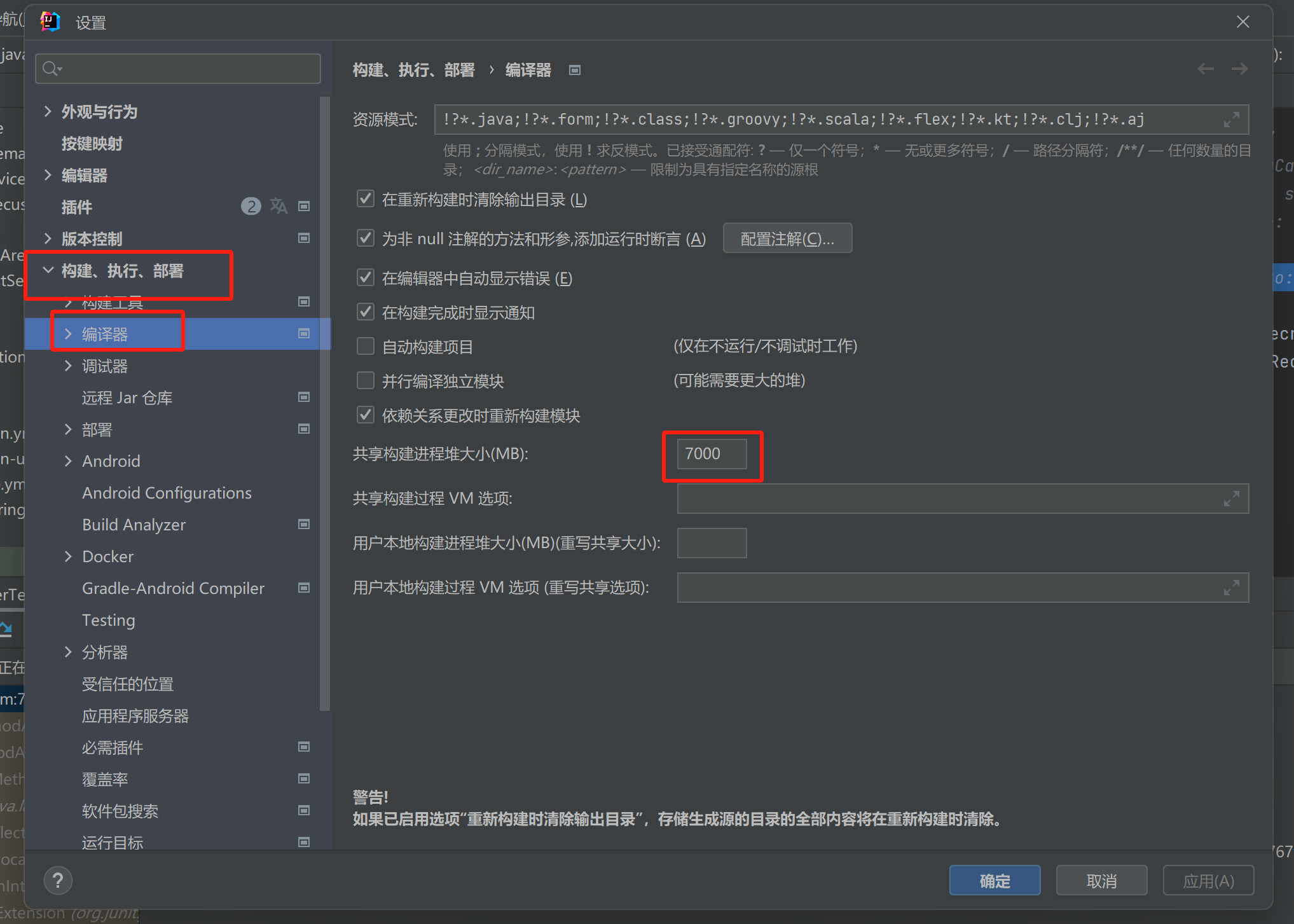
【记录坑点问题】IDEA运行:maven-resources-production:XX: OOM: Java heap space
问题:IDEA出现maven-resources-production:operation-service: java.lang.OutOfMemoryError: Java heap space 解决方案:将编译的堆内存增加一点 位置:设置setting-》构建菜单build-》编译器Complier...

用js实现常见排序算法
以下是几种常见排序算法的 JS实现,包括选择排序、冒泡排序、插入排序、快速排序和归并排序,以及每种算法的特点和复杂度分析 1. 选择排序(Selection Sort) 核心思想:每次从未排序部分选择最小元素,与未排…...

Netty自定义协议解析
目录 自定义协议设计 实现消息解码器 实现消息编码器 自定义消息对象 配置ChannelPipeline Netty提供了强大的编解码器抽象基类,这些基类能够帮助开发者快速实现自定义协议的解析。 自定义协议设计 在实现自定义协议解析之前,需要明确协议的具体格式。例如,一个简单的…...

【QT】qtdesigner中将控件提升为自定义控件后,css设置样式不生效(已解决,图文详情)
目录 0.背景 1.解决思路 2.详细代码 0.背景 实际项目中遇到的问题,描述如下: 我在qtdesigner用界面拖了一个QTableView控件,object name为【tableView_electrode】,然后【提升为】了自定义的类【Steer_Electrode_Table】&…...

MySQL用户远程访问权限设置
mysql相关指令 一. MySQL给用户添加远程访问权限1. 创建或者修改用户权限方法一:创建用户并授予远程访问权限方法二:修改现有用户的访问限制方法三:授予特定数据库的特定权限 2. 修改 MySQL 配置文件3. 安全最佳实践4. 测试远程连接5. 撤销权…...
