配置主机名与ip的映射关系
本次进行简单的小实验
通过在windows上配置主机名与IP地址的映射关系,达到我们在xshell或其他远程连接设备上,不用IP地址登陆,只需要用主机名就能实现登陆的效果
配置
首先 需要查看自己虚拟机的IP地址,找到ens33或者ens160下面的主IP
ip ad
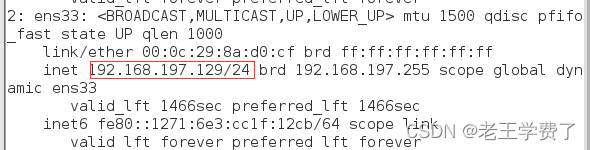
可以看到,我这台是192.168.197.129,下面我们进行配置
在windows下,使用管理员身份打开记事本,一定要用管理员身份,不然改不了的
第二步,文件---打开如下路径:C:\Windows\System32\drivers\etc,找到hosts文件!!
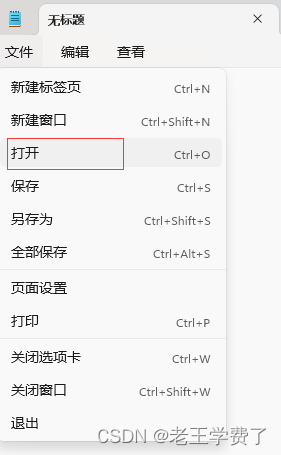
第三步 有些人可能看到没有,点击所有文件
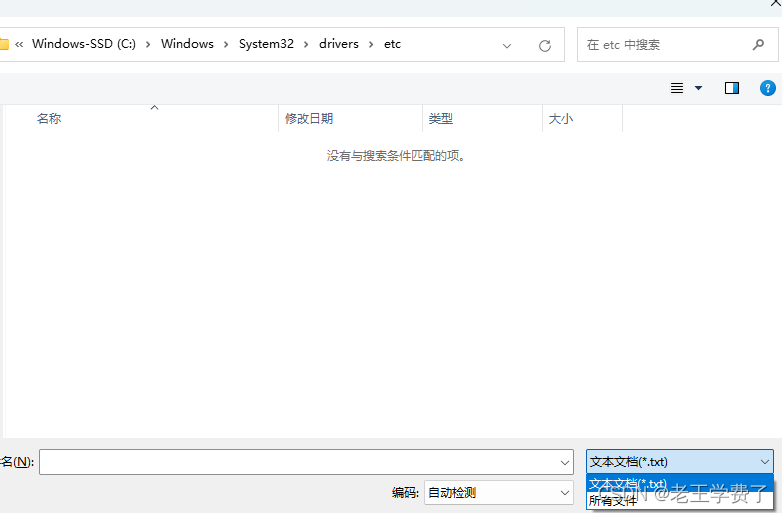
找到hosts文件 打开,添加如下:
你的ip 主机名
如
192.168.197.129 centos
:你的主机名是指@后面的名字
![]()
CTRL+s保存更改
连接
然后输入你的用户名以及密码即可连接成功
ps:你也可以直接用ssh 用户名@你的主机名来连接成功,这样可省去你的IP地址
ps: 如果觉得主机名太难太长,默认为locahost,你可以使用以下命令去更改:
hostnamectl set-hostname centos
相关文章:

配置主机名与ip的映射关系
本次进行简单的小实验 通过在windows上配置主机名与IP地址的映射关系,达到我们在xshell或其他远程连接设备上,不用IP地址登陆,只需要用主机名就能实现登陆的效果 配置 首先 需要查看自己虚拟机的IP地址,找到ens33或者ens160…...

Spring Cache简单介绍和使用
目录 一、简介 二、使用默认ConcurrentMapManager (一)创建数据库和表 (二)创建boot项目 (三)使用Api 1、EnableCaching 2、CachePut 3、cacheable 4、CacheEvict 三、使用redis作为cache 一、简…...

ECCV 2022|面向精确的主动相机定位算法
标题:ECCV 2022,山东大学、北大、腾讯AILab、斯坦福和三维家联合提出,面向精确的主动相机定位算法项目地址:https://github.com/qhFang/AccurateACL.文章:Towards Accurate Active Camera Localization(ECCV 2022&…...

web实现环形旋转、圆形、弧形、querySelectorAll、querySelector、clientWidth、sin、cos、PI
文章目录1、HTML部分2、css部分3、JavaScript部分4、微信小程序演示1、HTML部分 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge">&l…...

PyCharm+Python+Selenium自动化测试动态验证码识别
driver.find_element(byBy.ID,valueUSERID).send_keys("admin")driver.find_element(byBy.ID,valuePASSWORD_VIEW).send_keys("123456")#ocr识别原理:先根据验证码的class dl_yzm定位到验证码图片,然后将验证码截图保存,…...

git版本回退简单记录
简单记录git版本回退的命令,参考的是这篇文章1 首先查看以前存档的版本: git log1. 知道要回退的版本和现在的版本差了多少代 回退上一代版本(1个以前) git reset –hard HEAD^回退上上一代版本(2个以前࿰…...
QT入门Display Widgets之QLine、QLcdNumber、QTextBrowser
目录 一、QLine界面相关 1、布局介绍 2、界面基本属性 二、QLCDNumber的介绍 1、界面布局 2、定时器代码测试 三、QTextBrowser 此文为作者原创,创作不易,转载请标明出处! 一、QLine界面相关 1、布局介绍 先看下界面中创建个Q…...

Spring学习笔记
目录1 IOC容器1.1 概念1.2 IOC的底层原理1.3 Spring中IOC容器的两种实现方式(两个接口)1.3.1 BeanFactory接口1.3.2 ApplicationContext接口1.3.3 为什么开发中使用ApplicationContext接口1.3.4 ApplicationContext接口的两个实现类1.4 IOC操作之bean管理1.4.0 bean是什么&…...

数据的标准化处理
假设各个指标之间的水平相差很大,此时直接使用原始指标进行分析时,数值较大的指标,在评价模型中的绝对作用就会显得较为突出和重要,而数值较小的指标,其作用则可能就会显得微不足道。 因此,为了统一比较的标…...

性能优化|记一次线上OOM问题处理
概述最近线上监控发现 OOM 涨幅较大,因此去尝试定位和修复这个问题,在修复了一些内存泄漏和大对象占用问题后, OOM 依旧未达到正常标准,在这些新上报的 hprof 文件中,发现几乎所有 case 中都有个叫 FinalizerReference 的对象&…...

Vue动态粒子特效插件(背景线条吸附动画)
目录 效果图: 一、安装: 二、引入 main.js 文件: 三、使用: 四、属性说明: 效果图: 一、安装: npm install vue-particles --save 二、引入 main.js 文件: import VueParticles…...

【Java 类】002-类、属性、方法、代码块
【Java 类】002-类、属性、方法、代码块 文章目录【Java 类】002-类、属性、方法、代码块一、类1、类与对象2、类的作用3、创建与使用类类结构创建类调用类运行结果4、Java 类的执行过程5、封装、继承、多态、抽象类、内部类、接口、枚举、记录、注解等二、属性1、概述2、类型3…...

Ubuntu Linux 编译安装的基本步骤
文章目录1 基本步骤若报错: No such file or directory2 解压 tar.bz2文件参考:1 基本步骤 解压: tar -zxvf file.tar.gz 进入解压后的文件夹: cd file 源码编译安装 ./configure # ./configmakesudo make install 若报错&…...
day59反刍笔记
1.本地环境安装vue后,没有vue.js文件,只有vue.cjs.js文件, 引用后也无法正常使用,看npm install vue后的文件夹中没有vue.js文件_找不到vue.js_一枝风的博客-CSDN博客 老哥的博客后得到启发,将原本的命令由࿱…...

【阅读笔记】你不知道的Javascript--强制类型转换4
目录强制类型转换基本概念JSONboolean强转归纳其他知识点被诟病的安全使用隐式强转法则抽象关系比较语法表达式变动强制类型转换 基本概念 类型转换发生在静态类型语言的编译阶段; 强制类型转换则发生在动态类型语言的运行时(runtime) JSON…...
)
华为OD机试真题Python实现【有效子字符串】真题+解题思路+代码(20222023)
有效子字符串 题目 输入两个字符串S和L,都只包含小写字母, S长度 <= 100,L长度 <= 500000, 判断S是否是L的有效子字符串, 判定规则:S中的每个字符在L中都能找到(可以不连续) 且S在L中字符的前后顺序与S中顺序要保持一致 例如: S="ace"是L="abcd…...
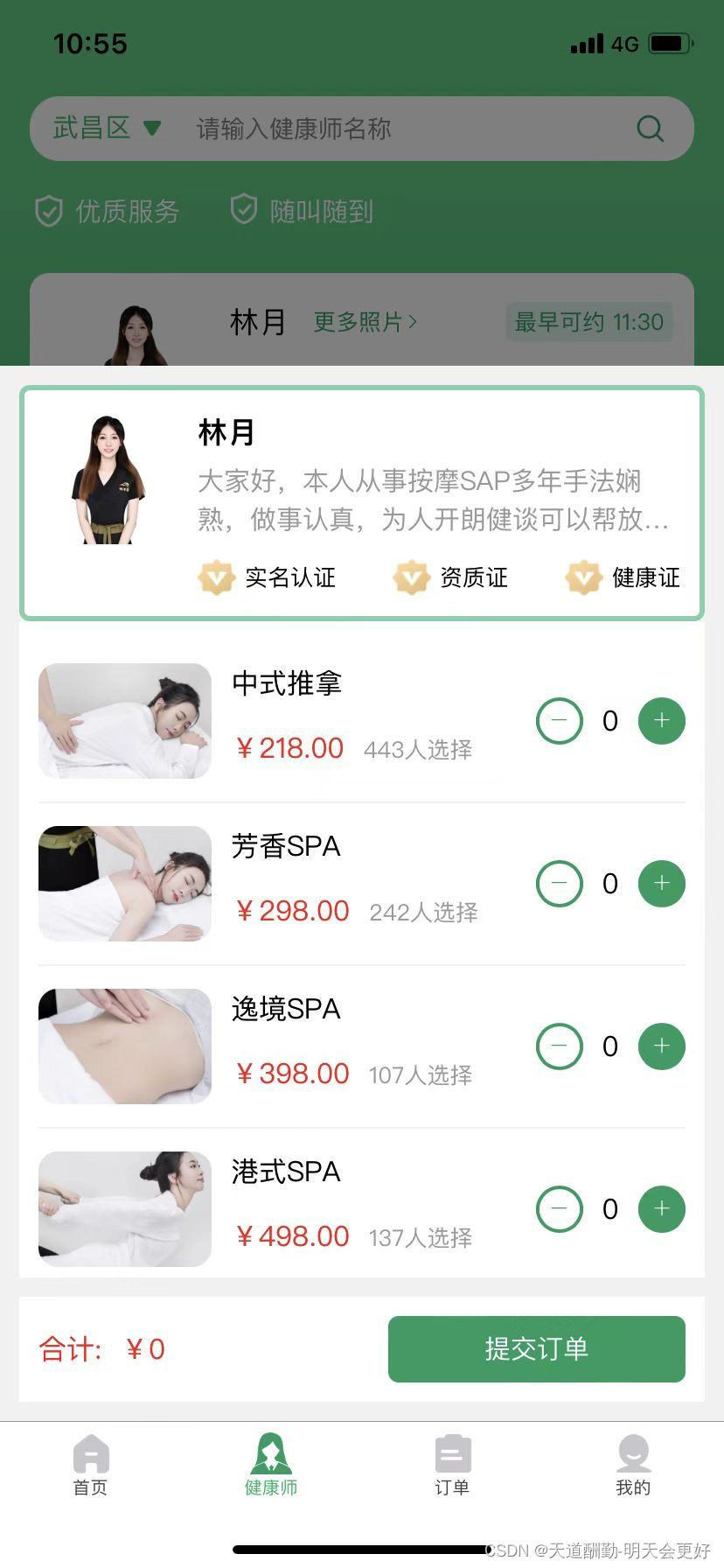
上门按摩预约APP源码-东郊到家源码(开发,PHP,平台搭建)
一、什么是上门按摩预约APP源码? 上门按摩预约APP源码是一款家政服务类型的APP,可以帮忙用户在家就能享受按摩的服务。APP源码分两端,一端是用户端,另外一端是技师端。采用的技术,前端是安卓IOS,后端是PHP&…...
STL讲解——模拟实现vector
STL讲解——模拟实现vector vector深度剖析 在STL源码中,发现vector定义的并不是 start、size、capacity,而是start、finish、end_of_storage. 这样就可以得到size()和capacity()。 sizefinish-start capacityend_of_storage-start 扩容可能是本地扩容也…...

各种经典排序算法介绍及实现源码
一,冒泡排序(Bubble Sort) 排序算法是程序员必须了解和熟悉的一类算法,排序算法有很多种,基础的如:冒泡、插入、选择、快速、归并、计数、基数和桶排序等。 冒泡排序只会操作相邻的两个数据。每次冒泡操作都会对相邻的两个元素进行比较,看是否满足大小关系要求,如果不…...

历史大讲堂:这是真·图形化 苹果系统历史回顾(上)
众所周知,米国有个非常牛掰的公司叫苹果,想必大家对这个logo不陌生吧。 目前已发布的苹果产品有iPhone、iPad、iPod等等,简直花样繁多,而且各种功能很好用,我的手机就是一部苹果iPhone X。 等一下,似乎扯远…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...
