二分练习题——123
123
二分+等差数列求和+前缀和数组
题目分析

连续一段的和我们想到了前缀和,但是这里的l和r的范围为1e12,明显不能用O(n)的时间复杂度去求前缀和。那么我们开始观察序列的特点,可以按照等差数列对序列进行分块。如上图,在求前10个数的和的时候,我们可以这样求1+3(1+2)+6(1+2+3)+10(1+2+3+4)=20。我们不需要遍历10次就可以求出来。求前缀和代码如下
sum = new long[1500010];
for (int i = 1; i <= 1500000; i++) {t += i;sum[i] = sum[i-1]+t;
}
这里的t最开始等于1,是第一块的数字和,然后等于3,是第二块数字的和,然后等于6是第三块数字的和,以此类推。sum[i]表示的是分块后前i块包含数字的和。
我们可以求出前n块数字的和,那么我们需要知道第l个数字是在哪一块里面,然后求第l个数字是所在块的第几个数字。因为对于最后一块来说,不是所有的数字都会被包含进来,我们要单独对最后一块求数字和。
第一阶段利用二分求第x个数所在的块

图1
如图1所示,我们可以把这个序列分块,第一块有1个数,第二块有2个数,第三块有3个数,第四块有4个数,每一块拥有数的个数是一个等差数列。现在要找到序列中第x个数所在的块数,假设x=3,那么第x个数在第2块中,如果x=4,那么第x个数在第3块中。求第x个数所在的块数,就是求从左往右数,前缀和第一个大于等于x的块。
比如第2块的前缀和就是3,第三块的前缀和就是5。这个可以用二分去求。
int l = 1;int r = 1500000;//最多可以分的块数while(l < r) {int mid = (l + r) / 2;if(sum(mid) < x) {//求mid个块中包含的数字的个数,如果小于x,就是不符合条件,我要向左找l = mid + 1;}else {//符合条件,我要看前面的块是否也是大于等于x的r = mid;}}
这里的sum函数的作用就是求前mid块中包含的数字的个数,因为是等差数列,所以直接用等差数列的求和公式就可以了,sum函数如下
private static long sum(long x) { return (1L + x) * x / 2;
}
第二阶段求前x个数的前缀和
接下来分析二分结束之和我要怎么操作,我要求前x个数字的和。
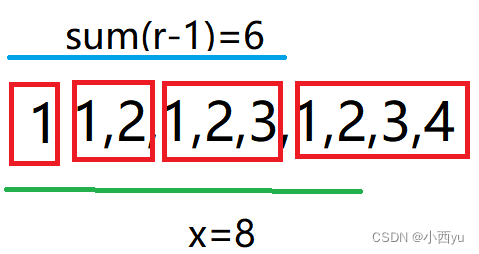
假设x=8,那么第x个数在第4块中,我还要知道,第x个数是第4块中的第几个数字。如图,第4块有4个数,第x个数第4块的第2个数上,那么第2个数是怎么来的呢?就是x-sum(r-1)=8-6=2。其实就是我二分算出来了第x个数在第r块上,那么我只需要把前r-1块包含的数的个数减去就算出来x是在第r块上的第几个数上了。结合上图更好理解。那么前x个数的和就是前r-1块包含数的和加上第r块里面前x-sum(r-1)个数的和。
某一块里面包含的数也是等差数列,求前n个数的和依然可以直接用sum(n)去求。而数组sum[r]里面记录的是前r块包含数字值的前缀和。所以二分结束后的代码是这样子的
private static long f(long x) {int l = 1;int r = 1500000;//最多可以分的块数while(l < r) {int mid = (l + r) / 2;if(sum(mid) < x) {//求mid个块中包含的数字的个数l = mid + 1;}else {r = mid;}}//r--是表示完整的块的个数r--;//就是上文里的r-1//x表示x处在他所在块的第几个位置,需要减去前面所有块包含的数的个数//本来要求x个数字,前r个块中已经包含了sum(r)个数字,第r+1个块x -= sum(r);//前r个块中已经包含了多少个数字return sum[r]+sum(x);
}
还是对于x=8的例子,二分求出来r=4,r–后,r=3,sum[3]=10。x-=sum(3)=8-6=2。sum[3]+sum(2)=10+3=13
注意这道题里对于sum函数的多次应用,但是不是每一次应用含义都是一样的。因为每一块包含的数字个数是等差数列,而每一块内每个数字形成的也是等差数列。
题目代码
import java.util.Scanner;
public class Main {
static long[] sum;
public static void main(String[] args) {Scanner scanner = new Scanner(System.in);long t = 0;//前缀和的预处理sum = new long[1500010];for (int i = 1; i <= 1500000; i++) {t += i;sum[i] = sum[i-1]+t;}int n = scanner.nextInt();while(n-- > 0) {long l = scanner.nextLong();long r = scanner.nextLong();System.out.println(f(r)-f(l-1));//f(r)求的是序列中前r个数的和}
}
//二分 二分求的是x在哪一块中 n*(n-1)/2>l的第一个n
private static long f(long x) {int l = 1;int r = 1500000;//最多可以分的块数while(l < r) {int mid = (l + r) / 2;if(sum(mid) < x) {//求mid个块中包含的数字的个数l = mid + 1;}else {r = mid;}}//r--是表示完整的块的个数r--;//x表示x处在他所在块的第几个位置,需要减去前面所有块包含的数的个数//本来要求x个数字,前r个块中已经包含了sum(r)个数字,第r+1个块x -= sum(r);//前r个块中已经包含了多少个数字return sum[r]+sum(x);
}
//sum函数求前x块包含的数的个数,同时也可以表示某一个块中,前x个数的总和
private static long sum(long x) {// TODO Auto-generated method stub return (1L + x) * x / 2;
}
}
相关文章:
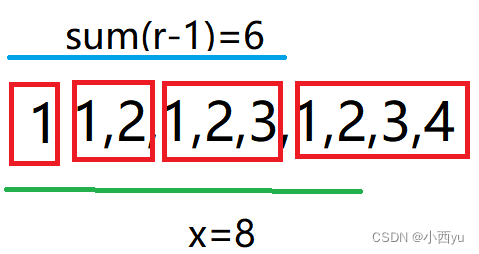
二分练习题——123
123 二分等差数列求和前缀和数组 题目分析 连续一段的和我们想到了前缀和,但是这里的l和r的范围为1e12,明显不能用O(n)的时间复杂度去求前缀和。那么我们开始观察序列的特点,可以按照等差数列对序列进行分块。如上图,在求前10个…...
淘宝详情数据采集(商品上货,数据分析,属性详情,价格监控),海量数据值得get
淘宝详情数据采集涉及多个环节,包括商品上货、数据分析、属性详情以及价格监控等。在采集这些数据时,尤其是面对海量数据时,需要采取有效的方法和技术来确保数据的准确性和完整性。以下是一些关于淘宝详情数据采集的建议: 请求示…...
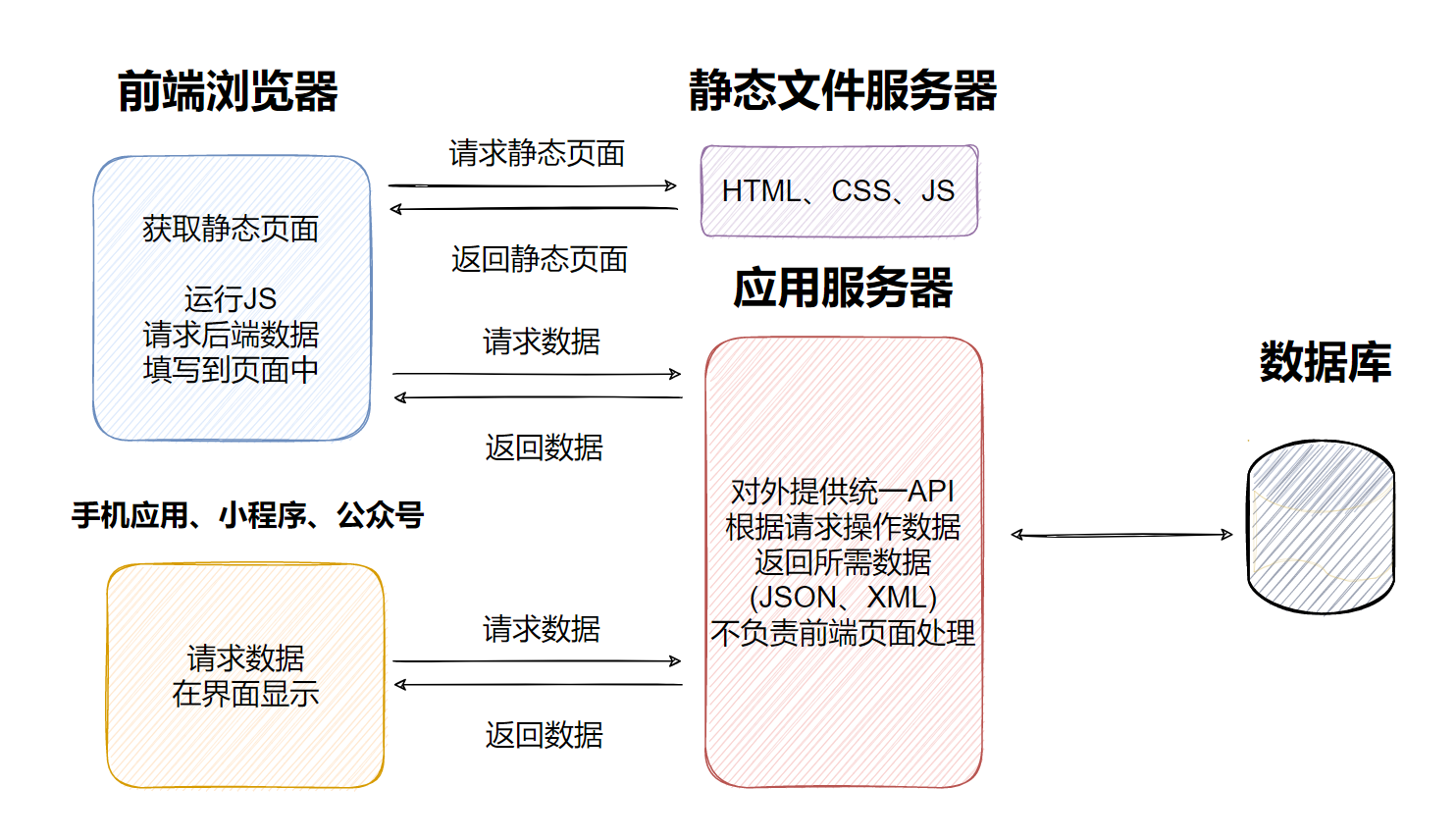
Django之Web应用架构模式
一、Web应用架构模式 在开发Web应用中,有两种模式 1.1、前后端不分离 在前后端不分离的应用模式中,前端页面看到的效果都是由后端控制,由后端渲染页面或重定向,也就是后端需要控制前端的展示。前端与后端的耦合度很高 1.2、前后端分离 在前后端分离的应用模式中,后端仅返…...

GPT提示词分享 —— 口播脚本
可用于撰写视频、直播、播客、分镜头和其他口语内容的脚本。 提示词👇 请以人的口吻,采用缩略语、成语、过渡短语、感叹词、悬垂修饰语和口语化语言,避免重复短语和不自然的句子结构,撰写一篇关于 [主题] 的文章。 GPT3.5&#…...
笔记本作为其他主机显示屏(HDMI采集器)
前言: 我打算打笔记本作为显示屏来用,连上工控机,这不是贼方便吗 操作: 一、必需品 HDMI采集器一个 可以去绿联买一个,便宜的就行,我的大概就长这样 win10下载 PotPlayer 软件 下载链接:h…...
02.percona Toolkit工具pt-archiver命令实践
1.命令作用 Percona Toolkit有的32个命令,可以分为7大类 工具类别 工具命令 工具作用 备注 开发类 pt-duplicate-key-checker 列出并删除重复的索引和外键 pt-online-schema-change 在线修改表结构 pt-query-advisor 分析查询语句,并给出建议&#x…...

【天狼启航者】研究计划
“造车”,预计在4月中旬展开(嵌入式蓝桥杯比赛结束后),这里先计划一下,不断更新。 基本要求: 使用STM32F407系列芯片,使用FreeRTOS系统。 驱动程序必须要有强大的可移植性、模块化、低耦合、简…...
面试题 之 webpack
1.说说你对webpack理解?解决什么问题? Webpack 是实现前端项目的模块化,用于现代 JavaScript 应用程序的静态模块打包工具,被webpack 直接引用的资源打包进 bunde.js的资源,当webpack 处理应用程序时,它会在内部构建一…...

【机器学习之旅】概念启程、步骤前行、分类掌握与实践落地
🎈个人主页:豌豆射手^ 🎉欢迎 👍点赞✍评论⭐收藏 🤗收录专栏:机器学习 🤝希望本文对您有所裨益,如有不足之处,欢迎在评论区提出指正,让我们共同学习、交流进…...
外星人m18R2国行中文版原厂预装23H2原装Win11系统恢复带F12恢复重置
戴尔外星人m18R2国行中文版原厂预装23H2系统恢复安装 远程恢复安装:https://pan.baidu.com/s/166gtt2okmMmuPUL1Fo3Gpg?pwdm64f 提取码:m64f 1.自带原厂预装系统各驱动,主题,Logo,Office带所有Alienware主题壁纸、Alienware软件驱动 2.带…...
libVLC 视频抓图
Windows操作系统提供了多种便捷的截图方式,常见的有以下几种: 全屏截图:通过按下PrtSc键(Print Screen),可以截取整个屏幕的内容。截取的图像会保存在剪贴板中,可以通过CtrlV粘贴到图片编辑工具…...

Docker搭建LNMP环境实战(06):Docker及Docker-compose常用命令
Docker搭建LNMP环境实战(06):Docker及Docker-compose常用命令 此处列举了docker及docker-compose的常用命令,一方面可以做个了解,另一方面可以在需要的时候进行查阅。不一定要强行记忆,用多了就熟悉了。 1、…...

ClickHouse10-ClickHouse中Kafka表引擎
Kafka表引擎也是一种常见的表引擎,在很多大数据量的场景下,会从源通过Kafka将数据输送到ClickHouse,Kafka作为输送的方式,ClickHouse作为存储引擎与查询引擎,大数据量的数据可以得到快速的、高压缩的存储。 Kafka大家…...

Encoding类
Encoding System.Text.Encoding 是 C# 中用于处理字符编码和字符串与字节之间转换的类。它提供了各种静态方法和属性,**用于在不同字符编码之间进行转换,**以及将字符串转换为字节数组或反之。 在处理多语言文本、文件、网络通信以及其他字符数据的场景…...

标定系列——预备知识-OpenCV中实现Rodrigues变换的函数(二)
标定系列——预备知识-OpenCV中实现Rodrigues变换的函数(二) 说明记录 说明 简单介绍罗德里格斯变换以及OpenCV中的实现函数 记录...

2014年认证杯SPSSPRO杯数学建模C题(第一阶段)土地储备方案的风险评估全过程文档及程序
2014年认证杯SPSSPRO杯数学建模 C题 土地储备方案的风险评估 原题再现: 土地储备,是指市、县人民政府国土资源管理部门为实现调控土地市场、促进土地资源合理利用目标,依法取得土地,进行前期开发、储存以备供应土地的行为。土地…...

我的编程之路:从非计算机专业到Java开发工程师的成长之路 | 学习路线 | Java | 零基础 | 学习资源 | 自学
小伙伴们好,我是「 行走的程序喵」,感谢您阅读本文,欢迎三连~ 😻 【Java基础】专栏,Java基础知识全面详解:👉点击直达 🐱 【Mybatis框架】专栏,入门到基于XML的配置、以…...
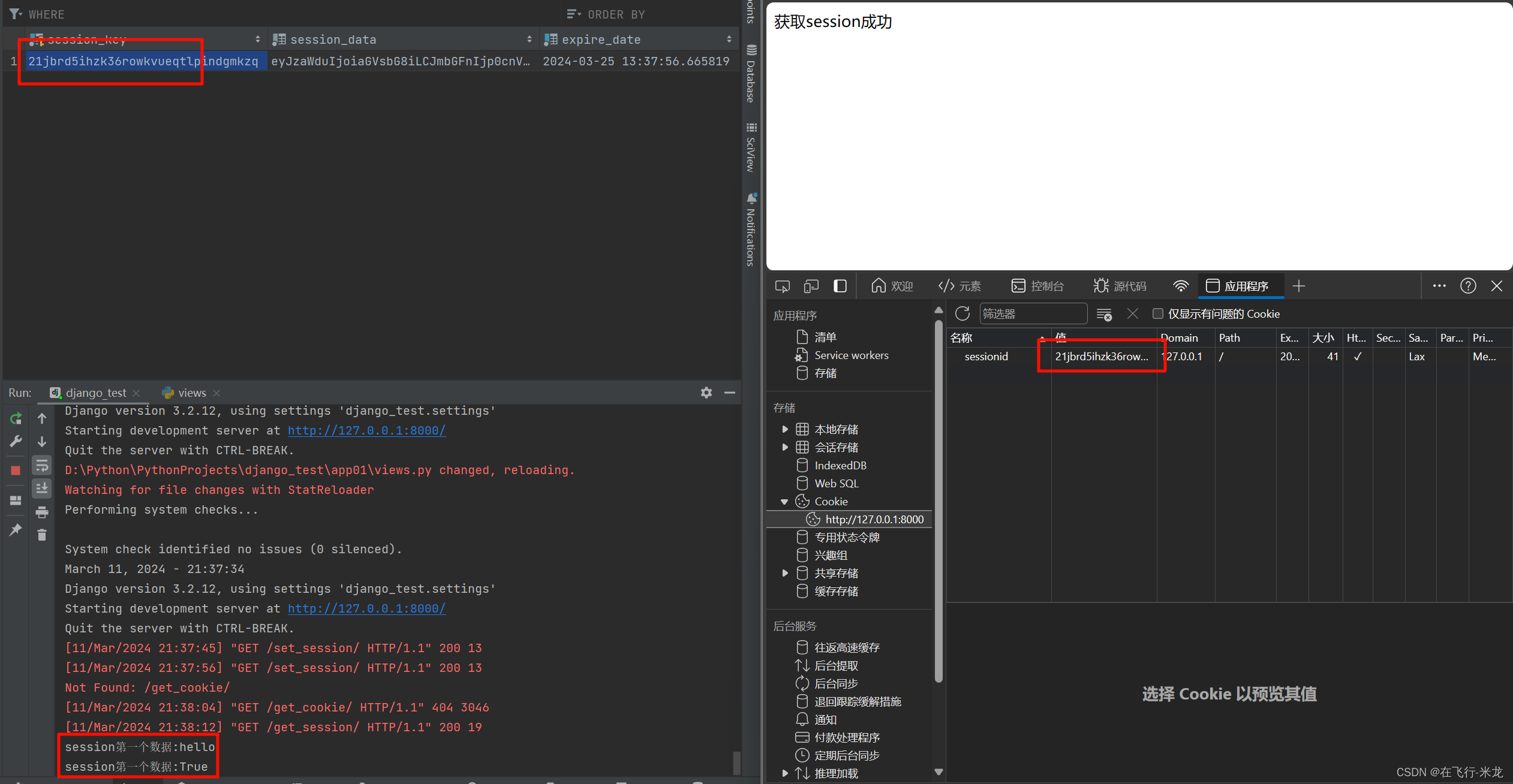
Django Cookie和Session
Django Cookie和Session 【一】介绍 【1】起因 HTTP协议四大特性 基于请求响应模式:客户端发送请求,服务端返回响应基于TCP/IP之上:作用于应用层之上的协议无状态:HTTP协议本身不保存客户端信息短链接:1.0默认使用短…...
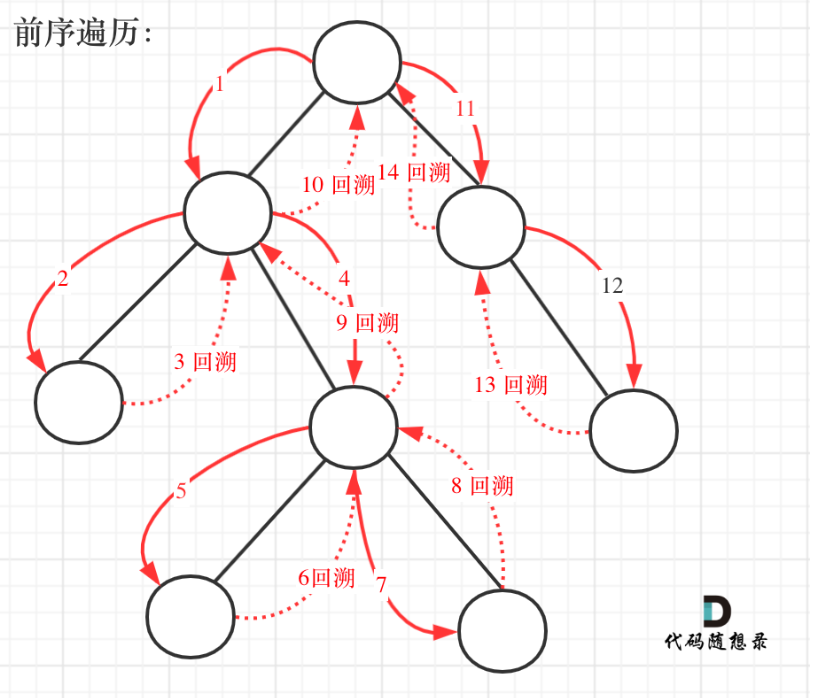
【算法刷题 | 二叉树 04】3.27(翻转二叉树、对称二叉树、完全二叉树的节点个数、平衡二叉树、完全二叉树的所有路径)
文章目录 6.翻转二叉树6.1问题6.2解法一:递归6.2.1递归思路(1)确定递归函数的参数和返回值(2)确定终止条件(3)确定单层递归的逻辑 6.2.2全部代码 6.3解法二:层序遍历 7.对称二叉树7.…...
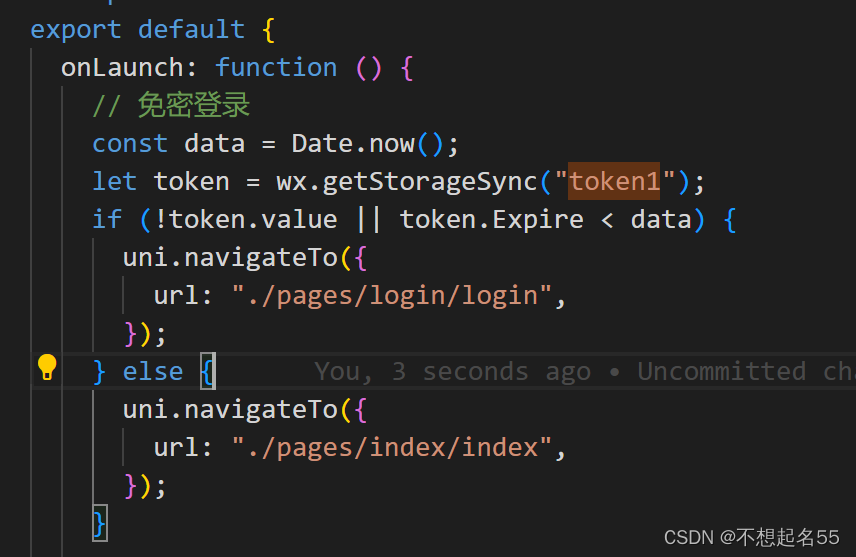
【uniapp】uniapp实现免密登录
文章目录 一、概要二、整体架构流程三、技术名词解释四 、技术细节1.存取token有效期?2.使用setStorageSync而不使用setStorage?3.使用onLaunch而不使用全局路由? 一、概要 打开一个网页或小程序的时候,我们有时候会自动进入主页…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...

车载诊断架构 --- ZEVonUDS(J1979-3)简介第一篇
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 做到欲望极简,了解自己的真实欲望,不受外在潮流的影响,不盲从,不跟风。把自己的精力全部用在自己。一是去掉多余,凡事找规律,基础是诚信;二是…...
