【算法刷题 | 二叉树 04】3.27(翻转二叉树、对称二叉树、完全二叉树的节点个数、平衡二叉树、完全二叉树的所有路径)
文章目录
- 6.翻转二叉树
- 6.1问题
- 6.2解法一:递归
- 6.2.1递归思路
- (1)确定递归函数的参数和返回值
- (2)确定终止条件
- (3)确定单层递归的逻辑
- 6.2.2全部代码
- 6.3解法二:层序遍历
- 7.对称二叉树
- 7.1问题
- 7.2解法一:递归
- 7.2.1递归思路
- (1)确定递归函数的参数和返回值
- (2)确定终止条件
- (3)确定单层递归的逻辑
- 7.2.2代码实现
- 7.3解法二:迭代法
- 8.完全二叉树的节点个数
- 8.1问题
- 8.2解法一:递归
- 8.3解法二:层序遍历
- 9.平衡二叉树
- 9.1问题
- 9.2解法一:递归
- 9.2.1递归思路
- (1)确定递归函数返回值和参数值
- (2)确定终止条件
- (3)确定递归逻辑
- 9.2.2代码
- 10.完全二叉树的所有路径
- 10.1问题
- 10.2解法一:前序遍历+回溯
- 10.2.1递归思路
- (1)确定递归函数参数以及返回值
- (2)确定递归终止条件
- (3)确定递归逻辑
- 10.2.2代码实现
6.翻转二叉树
6.1问题
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
- 示例一:
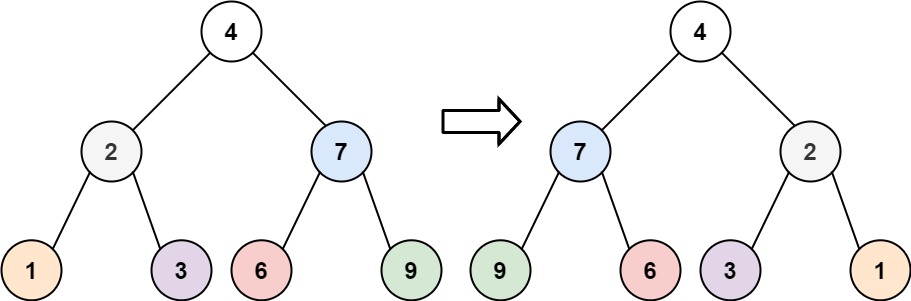
输入:root = [4,2,7,1,3,6,9]
输出:[4,7,2,9,6,3,1]
6.2解法一:递归
6.2.1递归思路
(1)确定递归函数的参数和返回值
- 题目为翻转根节点的左右孩子
- 最后返回根节点,即每次递归,传入TreeNode节点,返回该节点
TreeNode reverse(TreeNode node);
(2)确定终止条件
- 当递归到的该节点为空,即返回
if(node==null){return;
}
(3)确定单层递归的逻辑
- 当确定该节点不为空,先交换左、右孩子
- 再分别递归左孩子、右孩子
swap(node);
reverse(node.left);
reverse(node.right);
6.2.2全部代码
class Solution {public TreeNode invertTree(TreeNode root) {if(root==null){return root;}return reverse(root);}private TreeNode reverse(TreeNode node){if(node==null){return node;}swap(node);reverse(node.left);reverse(node.right);return node;}private void swap(TreeNode node){TreeNode tmp=node.left;node.left=node.right;node.right=tmp;}
}
6.3解法二:层序遍历
- 将每一个从队列取出来的元素,进行左孩子和有孩子的交换
class Solution {public TreeNode invertTree(TreeNode root) {//广度优先遍历Queue<TreeNode> queue=new LinkedList<>();if(root==null){return root;}queue.offer(root);while(!queue.isEmpty()){int size=queue.size();while(size>0){TreeNode node=queue.poll();swap(node);if(node.left!=null){queue.offer(node.left);}if(node.right!=null){queue.offer(node.right);}size--;}}return root;}private void swap(TreeNode node){TreeNode tmp=node.left;node.left=node.right;node.right=tmp;}
}
7.对称二叉树
7.1问题
给你一个二叉树的根节点 root , 检查它是否轴对称。
- 示例一:
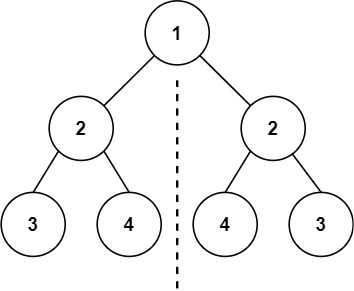
输入:root = [1,2,2,3,4,4,3]
输出:true
7.2解法一:递归
7.2.1递归思路
(1)确定递归函数的参数和返回值
- 比较的是根节点的两个子树是否是相互翻转的,进而判断这个树是不是对称树,所以要比较的是两个树,参数自然也是左子树节点和右子树节点。
- 返回值为boolean类型
boolean compare(TreeNode left,TreeNode right)
(2)确定终止条件
- 首先排除左孩子、右孩子节点有空的情况
- 左孩子为空,右孩子不为空:return false
- 左孩子不为空,右孩子为空:return false
- 左、右孩子均为空:return true
- 左、右孩子均不为空:
- 比较左右孩子的数值,不相同:return false
if (left == NULL && right != NULL) return false;
else if (left != NULL && right == NULL) return false;
else if (left == NULL && right == NULL) return true;
else if (left->val != right->val) return false; // 注意这里我没有使用else
(3)确定单层递归的逻辑
- 单层递归的逻辑就是处理左右节点都不为空,且数值相同的情况。
- 比较二叉树外侧是否对称:传入的是左节点的左孩子,右节点的右孩子。
- 比较内侧是否对称,传入左节点的右孩子,右节点的左孩子。
- 如果左右都对称就返回true ,有一侧不对称就返回false 。
boolean outside = compare(left.left, right.right); // 左子树:左、 右子树:右
boolean inside = compare(left.right, right.left); // 左子树:右、 右子树:左
boolean isSame = outside && inside; // 左子树:中、 右子树:中(逻辑处理)
return isSame;
7.2.2代码实现
class Solution {public boolean isSymmetric(TreeNode root) {if(root==null){return true;}return compare(root.left,root.right);}private boolean compare(TreeNode left,TreeNode right){if(left==null && right!=null){return false;}else if(left!=null && right==null){return false;}else if(left==null && right==null){return true;}else if(left.val!=right.val){return false;}//单层递归逻辑boolean out=compare(left.left,right.right);boolean in=compare(left.right,right.left);return (out&&in);}
}
7.3解法二:迭代法
- 使用队列来比较两个树(根节点的左右子树)是否相互翻转,(注意这不是层序遍历)
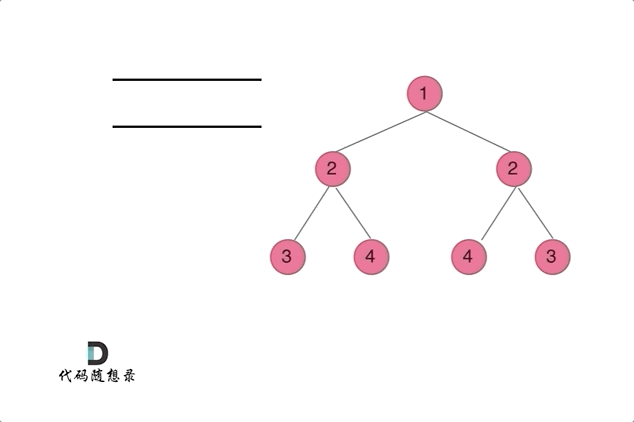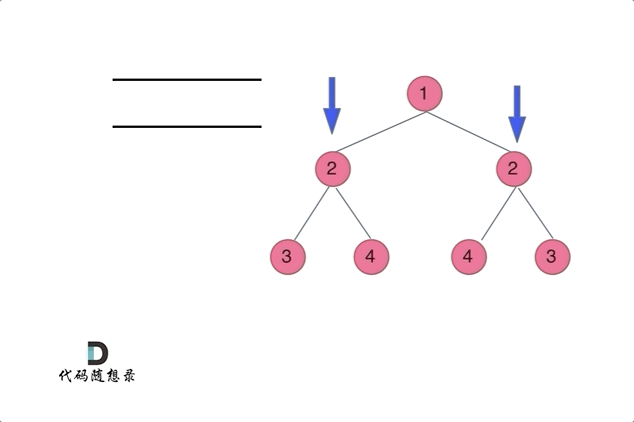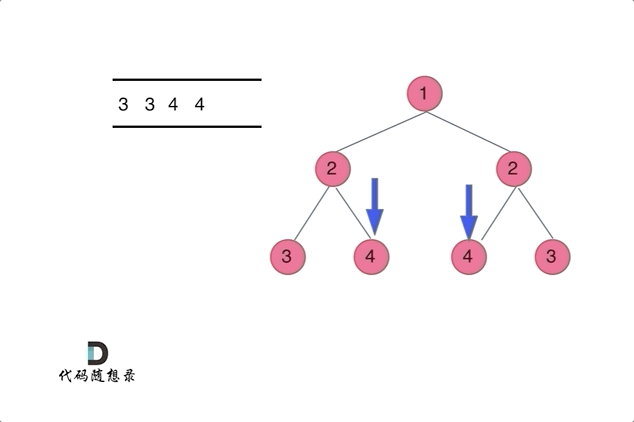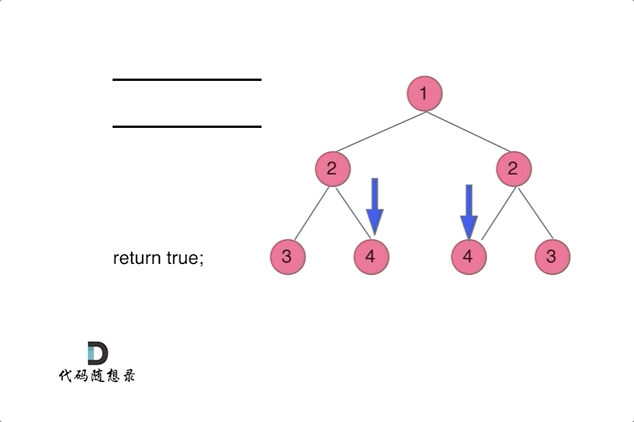
class Solution {public boolean isSymmetric(TreeNode root) {//迭代法if(root==null){return true;}Queue<TreeNode> queue=new LinkedList<>();//添加根节点的左右孩子queue.offer(root.left);queue.offer(root.right);while(!queue.isEmpty()){TreeNode left=queue.poll();TreeNode right=queue.poll();//1、判断两个节点是否均为空if(left==null && right==null){continue; //对称,结束此次循环,再次取出新的两个节点判断}//2、判断不符合对称条件if(left==null || right==null || (left.val!=right.val)){return false;}//3、添加新的两个节点:外层+内层queue.offer(left.left);queue.offer(right.right);queue.offer(left.right);queue.offer(right.left);}return true;}}
8.完全二叉树的节点个数
8.1问题
给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。
完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2h 个节点。
- 示例一:
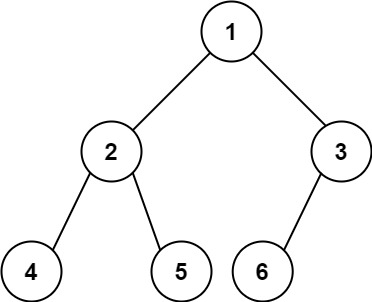
输入:root = [1,2,3,4,5,6]
输出:6
8.2解法一:递归
class Solution {public int countNodes(TreeNode root) {return count(root);}private int count(TreeNode node){if(node==null){return 0;}int leftCount=count(node.left);int rightCount=count(node.right);return leftCount+rightCount+1;}
}
8.3解法二:层序遍历
class Solution {public int countNodes(TreeNode root) {//广度优先遍历Queue<TreeNode> queue=new LinkedList<>();int count=0;if(root==null){return count;}queue.offer(root);while(!queue.isEmpty()){int size=queue.size();count+=size;while(size>0){TreeNode node=queue.poll();if(node.left!=null){queue.offer(node.left);}if(node.right!=null){queue.offer(node.right);}size--;}}return count;}}
9.平衡二叉树
9.1问题
给定一个二叉树,判断它是否是 平衡二叉树
- 示例一:
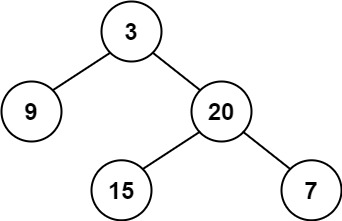
输入:root = [3,9,20,null,null,15,7]
输出:true
9.2解法一:递归
9.2.1递归思路
(1)确定递归函数返回值和参数值
- 题目为确定一棵树是否为平衡树
- 平衡树的定义:一棵树为空或者其左右节点的高度差的绝对值不超过1
- 即递归函数参数为一个树节点,返回值为该节点的高度(注意:若返回-1,则表明该树不平衡)
int isBalancedTree(TreeNode node)
(2)确定终止条件
- 若该节点为null,返回0
if(node==null){return 0;
}
(3)确定递归逻辑
- 传入一个节点,要求返回其高度,即需要求其左、右节点的高度
- 分别求完左、右节点的高度之后,判断其中是否为-1,若为-1,则返回-1,代表不平衡
- 若均不为-1,则求出该节点的平衡因子,若其绝对值超过1,则返回-1,代表不平衡
- 否则返回当前节点为根节点的树的最大高度
int leftHeight=isBalancedTree(node.left);
int rightHeight=isBalancedTree(node.right);
if(leftHeight==-1 || rightHeight==-1){return -1;
}
if(Math.abs(leftHeight-rightHeight)>1){return -1;
}
return 1+Math(leftHeight,rightHeight);
9.2.2代码
class Solution {public boolean isBalanced(TreeNode root) {return isBalancedTree(root)!=-1;}private int isBalancedTree(TreeNode node){if(node==null){return 0;}int leftHeight=isBalancedTree(node.left);int rightHeight=isBalancedTree(node.right);if(leftHeight==-1 || rightHeight==-1){return -1;}if(Math.abs(leftHeight-rightHeight)>1){return -1;}return 1+Math.max(leftHeight,rightHeight);}
}
10.完全二叉树的所有路径
10.1问题
给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。
叶子节点 是指没有子节点的节点。
- 示例一:
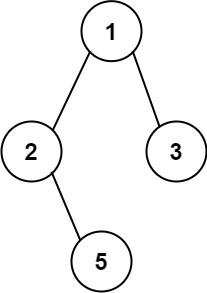
输入:root = [1,2,3,null,5]
输出:["1->2->5","1->3"]
10.2解法一:前序遍历+回溯
- 题目要求从根节点到叶子的路径,所以需要前序遍历,这样才方便让父节点指向孩子节点,找到对应的路径
- 把路径记录下来,需要回溯来回退一个路径再进入另一个路径。
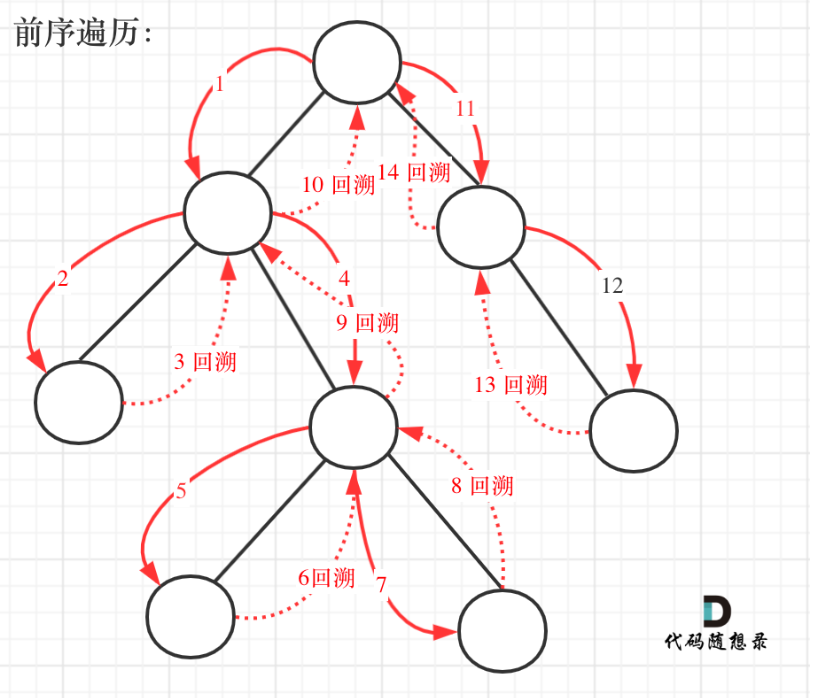
10.2.1递归思路
(1)确定递归函数参数以及返回值
- 求以node为根节点到达叶子节点的路径
- paths存放路径值
- res存放最终结果
void traversal(TreeNode node,List<Integer> paths,List<String> res)
(2)确定递归终止条件
- 当遍历到了叶子节点,即为一条完整的路径
- 取出paths的全部节点,并加入到res中
- 直接return
if(node.left==null && node.right==null){// 输出StringBuilder sb = new StringBuilder();// StringBuilder用来拼接字符串,速度更快for (int i = 0; i < paths.size() - 1; i++) {sb.append(paths.get(i)).append("->");}sb.append(paths.get(paths.size() - 1));// 记录最后一个节点res.add(sb.toString());// 收集一个路径return;
}
(3)确定递归逻辑
// 递归和回溯是同时进行,所以要放在同一个花括号里if (root.left != null) { // 左traversal(root.left, paths, res);paths.remove(paths.size() - 1);// 回溯}if (root.right != null) { // 右traversal(root.right, paths, res);paths.remove(paths.size() - 1);// 回溯}
10.2.2代码实现
class Solution {public List<String> binaryTreePaths(TreeNode root) {List<Integer> paths=new ArrayList<>();List<String> res=new ArrayList<>();traversal(root,paths,res);return res;}private void traversal(TreeNode node,List<Integer> paths,List<String> res){//1、前序遍历(中左右)处理该节点paths.add(node.val);//2、终止条件:该节点为叶子节点if(node.left==null && node.right==null){StringBuilder sb=new StringBuilder();for(int i=0;i<paths.size()-1;i++){sb.append(paths.get(i)).append("->");}//加入最后一个节点sb.append(paths.get(paths.size()-1));res.add(sb.toString());return;}//3、递归逻辑+回溯if(node.left!=null){traversal(node.left,paths,res);//回溯paths.remove(paths.size() - 1); //去除最后一个节点}if(node.right!=null){traversal(node.right,paths,res);//回溯paths.remove(paths.size() - 1); //去除最后一个节点}}
}
相关文章:

【算法刷题 | 二叉树 04】3.27(翻转二叉树、对称二叉树、完全二叉树的节点个数、平衡二叉树、完全二叉树的所有路径)
文章目录 6.翻转二叉树6.1问题6.2解法一:递归6.2.1递归思路(1)确定递归函数的参数和返回值(2)确定终止条件(3)确定单层递归的逻辑 6.2.2全部代码 6.3解法二:层序遍历 7.对称二叉树7.…...
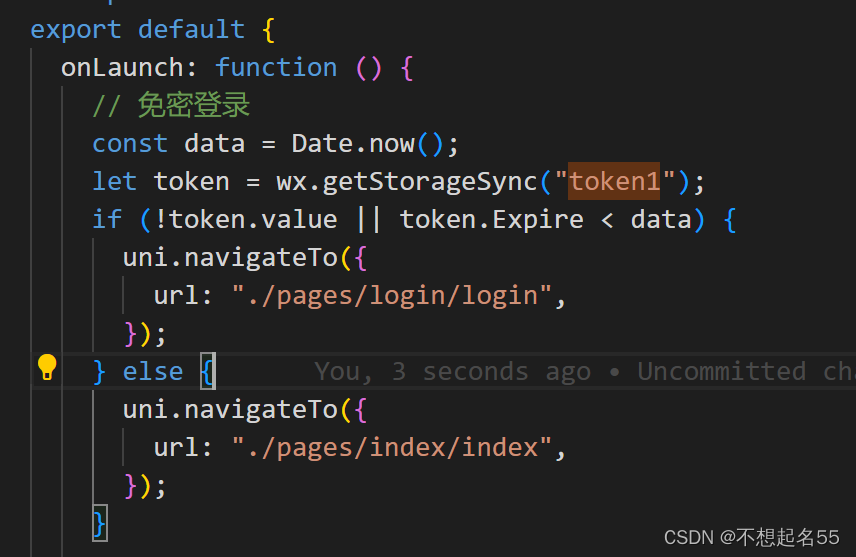
【uniapp】uniapp实现免密登录
文章目录 一、概要二、整体架构流程三、技术名词解释四 、技术细节1.存取token有效期?2.使用setStorageSync而不使用setStorage?3.使用onLaunch而不使用全局路由? 一、概要 打开一个网页或小程序的时候,我们有时候会自动进入主页…...

2024-03-27 问AI: 介绍一下深度学习中的 Darknet
文心一言 在深度学习中,Darknet是一个开源的神经网络框架,由Joseph Redmon开发,主要用于实现深度学习算法。它以其高效的实现和速度受到广泛关注,并在许多计算机视觉竞赛中取得了优异的结果。 Darknet的特点包括: 轻…...

POJ3037 + HDU-6714
两道最短路好题 POJ3037 手玩一下 发现每一点的速度可以直接搞出来,就是pow(2,h[1][1]-h[i][j])*V 那么从这个点出发到达别的点的耗费的时间都是上面这个数的倒数,然后直接跑最短路就好了 #include<iostream> #include<vector> #include<…...

Ubuntu搭建环境Cmake-Libtorch-Torchvision-PCL-VTK-OpenCV
Ubuntu搭建环境Cmake-Libtorch-Torchvision-PCL-VTK-OpenCV 安装Cmake安装libtorch安装torchvision安装PCL安装VTK安装OpenCV设置环境变量 仅供本人记录查阅使用 安装Cmake Cmake下载地址 解压 进入目录会看到只有 bin doc man share三个文件夹,没有 bootstrap文…...

分享多种mfc100u.dll丢失的解决方法(一键修复DLL丢失的方法)
在使用电脑过程中,我们经常会遇到一些陌生的DLL文件,例如mfc100u.dll。这些DLL文件是动态链接库(Dynamic Link Libraries)的缩写,它们包含了可以被多个程序共享的代码和数据。今天,我们将深入探讨mfc100u.d…...
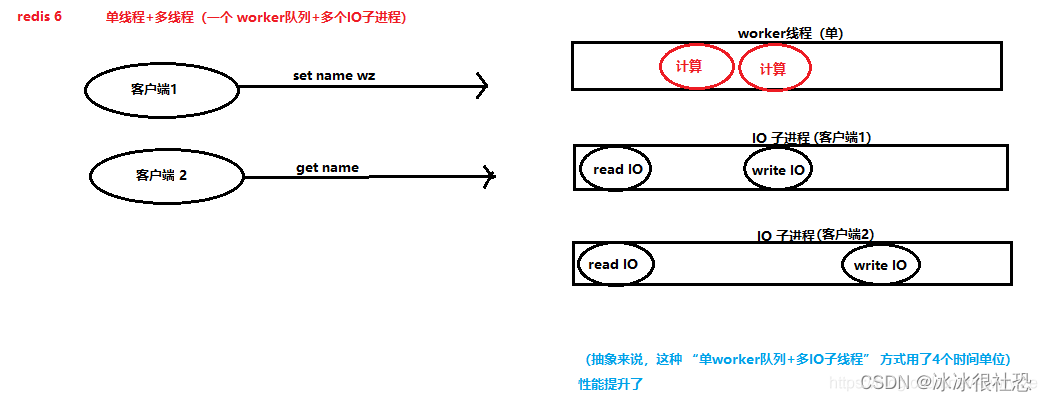
Redis是单线程还是多线程?(面试题)
1、Redis5及之前是单线程版本 2、Redis6开始引入多线程版本(实际上是 单线程多线程 版本) Redis6及之前版本(单线程) Redis5及之前的版本使用的是 单线程,也就是说只有一个 worker队列,所有的读写操作都要…...
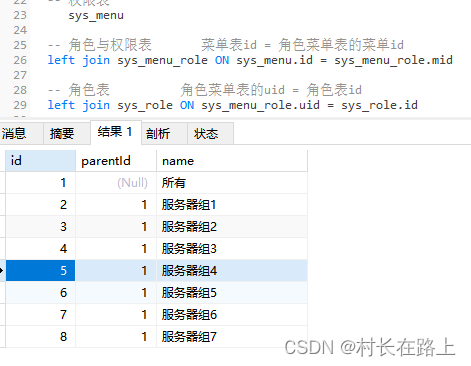
动态菜单设计
需求: 登录不同用户 显示不同的菜单 思路:根据用户id 左关联表 查询出对应的菜单选项 查询SQL select distinct-- 菜单表 去除重复记录sys_menu.id,sys_menu.parentId, sys_menu.name from -- 权限表sys_menu-- 角色与权限表 菜单表id 角色菜…...
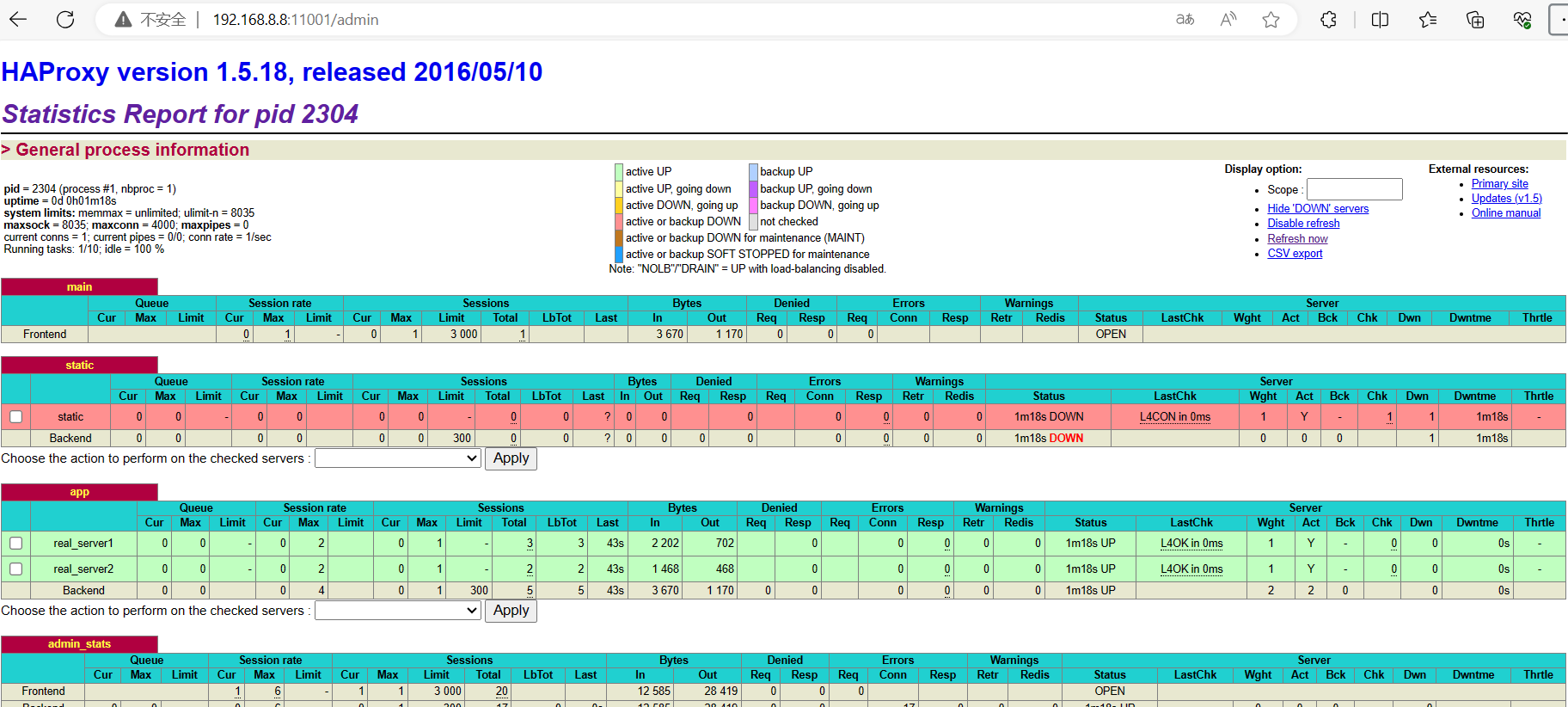
Haproxy负载均衡介绍即部署
haproxy的原理: 提供高可用、负载均衡以及基于TCP(四层)和HTTP(七层)应用的代理,支持虚拟主机,开源可靠的一款软件。 适用于哪些负载特别大的web站点,这些站点通常又需要回话保持和七…...

基于大语言模型的云故障根因分析|顶会EuroSys24论文
*马明华 微软主管研究员 2021年CCF国际AIOps挑战赛程序委员会主席(第四届) 2021年博士毕业于清华大学,2020年在佐治亚理工学院做访问学者。主要研究方向是智能运维(AIOps)、软件可靠性。近年来在ICSE、FSE、ATC、EuroS…...
Windows直接运行python程序
Windows直接运行python程序 一、新建bat脚本二、新建vbs脚本 一、新建bat脚本 新建bat批处理脚本,写入以下内容 echo off call conda activate pytorch python app.pyecho off:在此语句后所有运行的命令都不显示命令行本身,但是本身的指令是…...
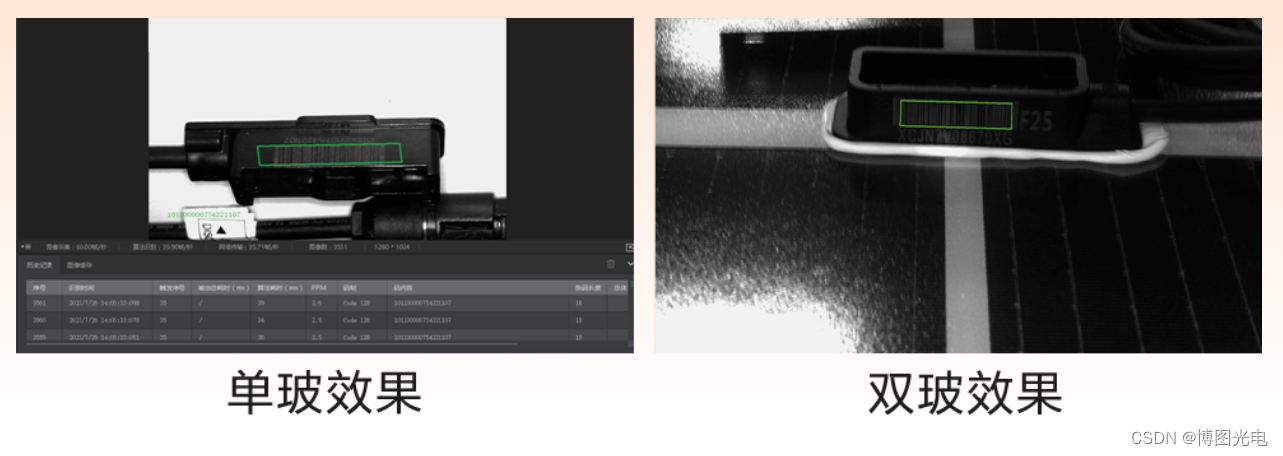
经典应用丨光伏行业扫码追溯新标杆,海康机器人AI智能读码器!
去年,光伏发电行业持续高速发展,我国仅在前九个月累计装机521.08GW,同比增长达到45.3%,已成为第二大电源类型超过水电。根据《2023中国与全球光伏发展白皮书》预测,到2030年,中国能够实现国家规划的风电和光…...

逆流而上的选择-积极生活,逆流而上
首先请大家看一个故事 李明坐在公司的开放式办公区,耳边是键盘敲击声的交响乐,眼前是一行行跳跃的代码。他的眼神有些恍惚,显示器的蓝光在他眼镜上反射出时代的光芒,这光芒既耀眼又刺眼。他即将35岁,在这个年纪&#x…...

SpringMVC基础Controller
文章目录 Controller 的编写和配置1. Controller 注解类型2. RequestMapping 注解类型3. 编写请求方法4. 请求参数和路径变量 Controller 的编写和配置 Controller 注解和 RequestMapping 注解是 Spring MVC 最重要的两个注解。 使用基于注解的控制器的优点如下: …...

spark 参数
spark.yarn.executor.memoryOverhead 默认值是384M Configuration - Spark 3.5.1 Documentation...
java调用jacob进行文件转换ppt转pdf或者png
java调用jacob进行文件转换ppt转pdf或者png 前情提要 最近项目上,遇到一个复杂的ppt,最终要求是要将ppt每一页转成图片原本这个是不难,网上一搜一大堆案例,外加我本身也比较精通aspose,那还不是分分钟搞定。结果就是…...

鸿蒙HarmonyOS应用开发之使用DevEco Studio模板构建NDK工程
NDK通过CMake和Ninja编译应用的C/C代码,编译过程如下图所示。 核心编译过程如下: 根据CMake配置脚本以及build-profile.json5中配置的externalNativeOptions构建参数,与缓存中的配置比对后,生成CMake命令并执行CMake。 执行Ninja…...
uniapp流浪动物救助小程序Java宠物领养小程序springboot
uniapp流浪动物救助小程序Java宠物领养小程序springboot 代码40块,需要的私聊 前台基于uniapp小程序 后台管理基于springbootvue前后端分离项目 开发语言:Java 框架:springboot vue JDK版本:JDK1.8(或11…...
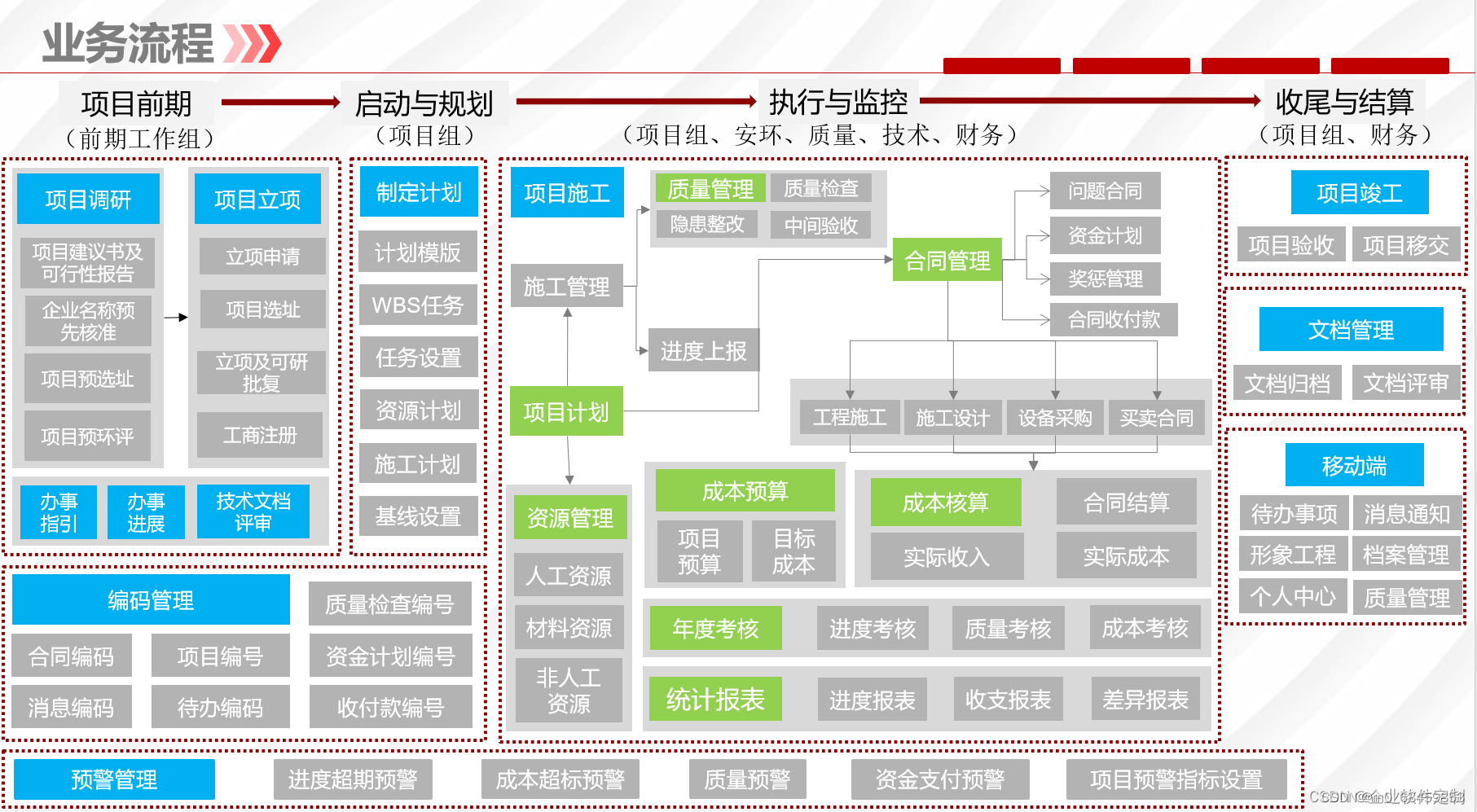
工程企业的未来选择:Java版工程项目管理系统平台与数字化管理的融合
在现代化的工程项目管理中,一套功能全面、操作便捷的系统至关重要。本文将介绍一个基于Spring Cloud和Spring Boot技术的Java版工程项目管理系统,结合Vue和ElementUI实现前后端分离。该系统涵盖了项目管理、合同管理、预警管理、竣工管理、质量管理等多个…...

Vue使用el-statistic和el-card显示大屏中的统计数据
一、页面内容: <el-row :gutter"20"><el-col :span"6"><el-card class"box-card"><div><el-statisticgroup-separator",":precision"2":value"value2":title"tit…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...
