POJ3037 + HDU-6714
两道最短路好题
POJ3037
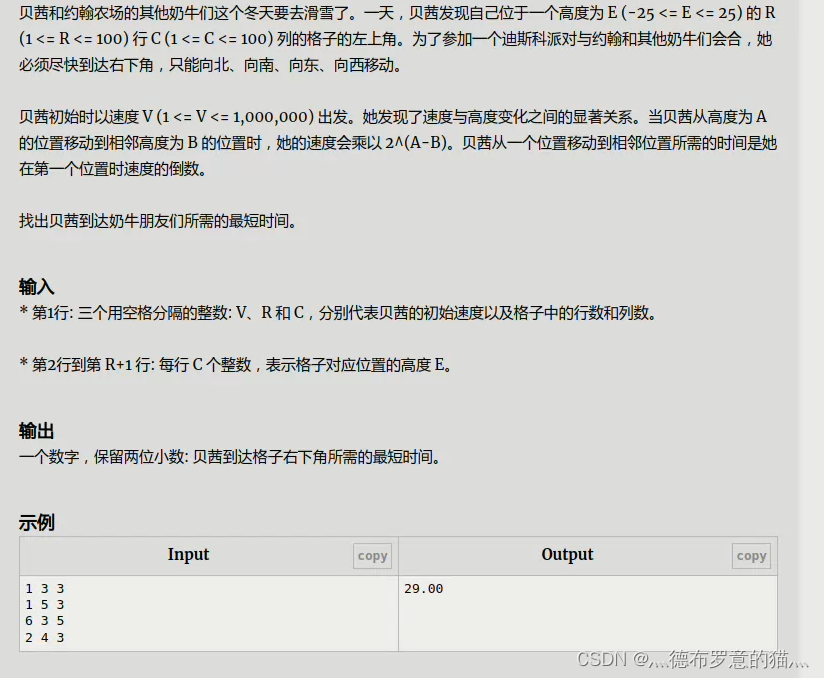
手玩一下 发现每一点的速度可以直接搞出来,就是pow(2,h[1][1]-h[i][j])*V
那么从这个点出发到达别的点的耗费的时间都是上面这个数的倒数,然后直接跑最短路就好了
#include<iostream>
#include<vector>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>
using namespace std;const int N = 1e5+10;
const int inf = 0x3f3f3f3f;
const int mod = 1e9+7;
int gcd(int a,int b){return b?a:gcd(b,a%b);}
int lcm(int a,int b){return a*b/gcd(a,b);}
int qmi(int a,int b,int mod){int res=1;while(b){if(b&1)res=res*a%mod;b>>=1;a=a*a%mod;}return res;}int n,q,m,v;
bool vis[1010][1010];
// int e[N],ne[N],w[N],h[N],idx;
// void add(int a,int b,int c){// e[idx] = b,ne[idx] = h[a],w[idx] = c,h[a] = idx++;
// }double vs[1010][1010];
double dist[1010][1010];
double h[1010][1010];void solve()
{cin>>v>>n>>m;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){double x;cin>>x;h[i][j] = x;vs[i][j] = pow(2,x-h[1][1])/v; dist[i][j] = 1e15;}}dist[1][1] = 0;queue<pair<int,int>>q;q.push(make_pair(1,1));int dx[] = {0,0,1,-1};int dy[] = {1,-1,0,0};vis[1][1] = true;while(q.size()){pair<int,int> t = q.front();q.pop();int x = t.first,y = t.second;vis[x][y] = false;//cout<<x<<" "<<y<<"\n";for(int i=0;i<4;i++){int temx = x+dx[i],temy = y+dy[i];if(temx<1||temx>n||temy<1||temy>m)continue;//cout<<temx<<" "<<temy<<"\n";if(dist[temx][temy]>dist[x][y]+vs[x][y]){dist[temx][temy] = dist[x][y]+vs[x][y];if(!vis[temx][temy]){vis[temx][temy] = true;q.push(make_pair(temx,temy));}}}}printf("%.2lf",dist[n][m]);}signed main()
{//ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int _;//cin>>_;_ = 1;while(_--)solve();return 0;
}HDU6714

这个dijk记数还是很有意思的,你得明白folyd的含义但是别被DP的含义绕进去
每次暴力的跑每一个点的单源最短路,然后当有中间点的时候你就更新一下就行了,没有中间的时候D【i】【j】就是一开始的距离,没有被更新,还是很有趣的,还是得想明白floyd的具体过程(好像不懂也行
一开始我就被绕进去了,一直在扣floyd 的含义来写这道,发现直接按上面的做法就好了
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
#define int long long
using pii = pair<int,int>;
const int N = 1e4+10;
const int inf = 0x3f3f3f3f;
const int mod = 998244353;
int gcd(int a,int b){return b?a:gcd(b,a%b);}
int lcm(int a,int b){return a*b/gcd(a,b);}
int qmi(int a,int b,int mod){int res=1;while(b){if(b&1)res=res*a%mod;b>>=1;a=a*a%mod;}return res;}int n,q,m;
int id[N];
int e[N],ne[N],w[N],h[N],idx;
void add(int a,int b,int c){e[idx] = b,ne[idx] = h[a],w[idx] = c,h[a] = idx++;
}bool vis[N];
ll dist[N];void dijkstra(int mid)
{memset(dist,0x3f,sizeof dist);memset(vis,0,sizeof vis);memset(id,0,sizeof id);priority_queue<pii,vector<pii>,greater<pii>>heap;heap.push({0,mid});dist[mid] = 0;while(heap.size()){auto t = heap.top();heap.pop();int ver = t.second;if(vis[ver])continue;vis[ver] = true;//cout<<ver<<"\n";for(int i=h[ver];~i;i=ne[i]){int j = e[i];if(dist[j]>dist[ver]+w[i]){dist[j] = dist[ver]+w[i];heap.push({dist[j],j});if(ver==mid)continue;id[j] = max(id[ver],ver);}else if(dist[j]==dist[ver]+w[i]){id[j] = min(id[j],max(id[ver],ver));}}}
}void solve()
{cin>>n>>m;memset(h,-1,sizeof h);idx = 0;while(m--){int a,b,c;cin>>a>>b>>c;add(a,b,c),add(b,a,c);}int ans = 0;for(int i=1;i<=n;i++){dijkstra(i);for(int j=1;j<=n;j++)ans = (id[j]+ans)%mod;//cout<<"\n";}cout<<ans;}signed main()
{ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int _;cin>>_;//_ = 1;while(_--)solve();return 0;
}相关文章:

POJ3037 + HDU-6714
两道最短路好题 POJ3037 手玩一下 发现每一点的速度可以直接搞出来,就是pow(2,h[1][1]-h[i][j])*V 那么从这个点出发到达别的点的耗费的时间都是上面这个数的倒数,然后直接跑最短路就好了 #include<iostream> #include<vector> #include<…...

Ubuntu搭建环境Cmake-Libtorch-Torchvision-PCL-VTK-OpenCV
Ubuntu搭建环境Cmake-Libtorch-Torchvision-PCL-VTK-OpenCV 安装Cmake安装libtorch安装torchvision安装PCL安装VTK安装OpenCV设置环境变量 仅供本人记录查阅使用 安装Cmake Cmake下载地址 解压 进入目录会看到只有 bin doc man share三个文件夹,没有 bootstrap文…...

分享多种mfc100u.dll丢失的解决方法(一键修复DLL丢失的方法)
在使用电脑过程中,我们经常会遇到一些陌生的DLL文件,例如mfc100u.dll。这些DLL文件是动态链接库(Dynamic Link Libraries)的缩写,它们包含了可以被多个程序共享的代码和数据。今天,我们将深入探讨mfc100u.d…...
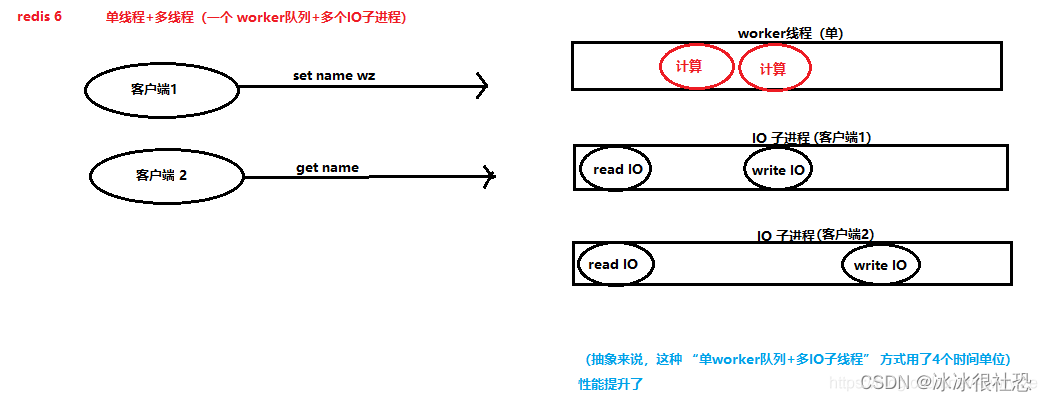
Redis是单线程还是多线程?(面试题)
1、Redis5及之前是单线程版本 2、Redis6开始引入多线程版本(实际上是 单线程多线程 版本) Redis6及之前版本(单线程) Redis5及之前的版本使用的是 单线程,也就是说只有一个 worker队列,所有的读写操作都要…...
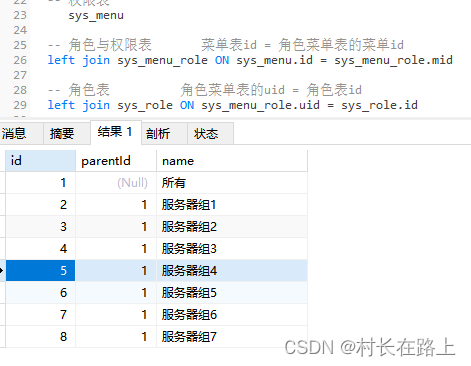
动态菜单设计
需求: 登录不同用户 显示不同的菜单 思路:根据用户id 左关联表 查询出对应的菜单选项 查询SQL select distinct-- 菜单表 去除重复记录sys_menu.id,sys_menu.parentId, sys_menu.name from -- 权限表sys_menu-- 角色与权限表 菜单表id 角色菜…...
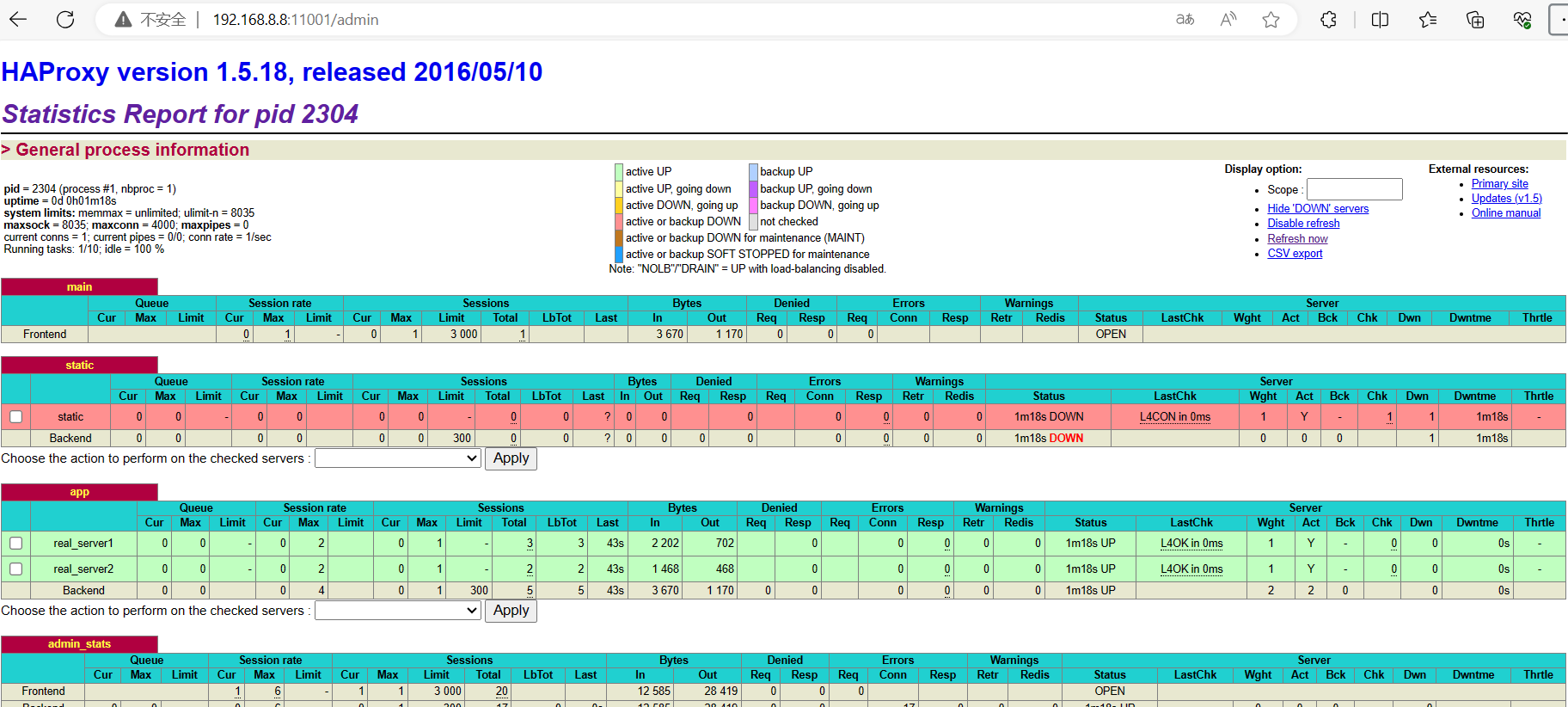
Haproxy负载均衡介绍即部署
haproxy的原理: 提供高可用、负载均衡以及基于TCP(四层)和HTTP(七层)应用的代理,支持虚拟主机,开源可靠的一款软件。 适用于哪些负载特别大的web站点,这些站点通常又需要回话保持和七…...

基于大语言模型的云故障根因分析|顶会EuroSys24论文
*马明华 微软主管研究员 2021年CCF国际AIOps挑战赛程序委员会主席(第四届) 2021年博士毕业于清华大学,2020年在佐治亚理工学院做访问学者。主要研究方向是智能运维(AIOps)、软件可靠性。近年来在ICSE、FSE、ATC、EuroS…...
Windows直接运行python程序
Windows直接运行python程序 一、新建bat脚本二、新建vbs脚本 一、新建bat脚本 新建bat批处理脚本,写入以下内容 echo off call conda activate pytorch python app.pyecho off:在此语句后所有运行的命令都不显示命令行本身,但是本身的指令是…...
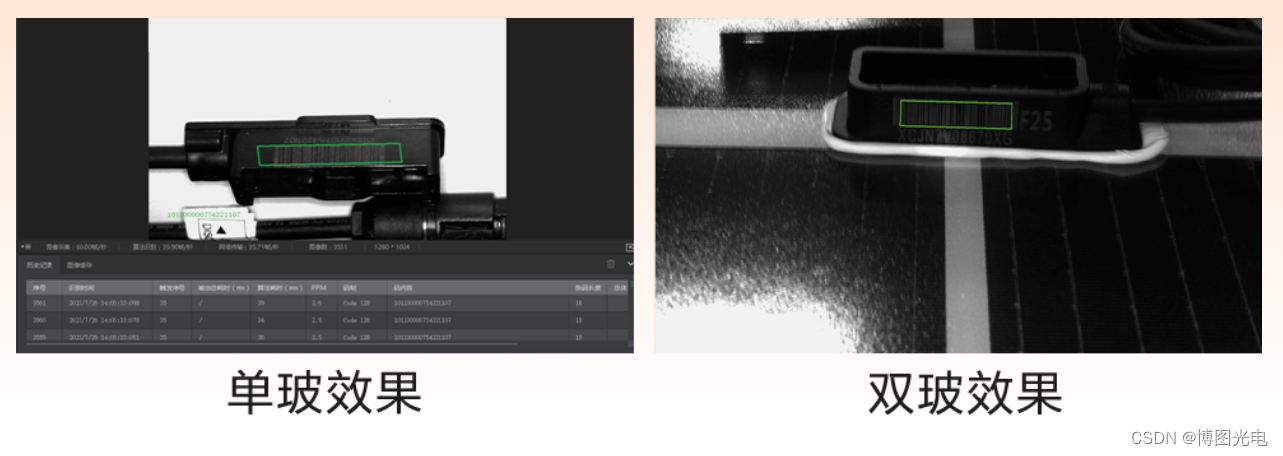
经典应用丨光伏行业扫码追溯新标杆,海康机器人AI智能读码器!
去年,光伏发电行业持续高速发展,我国仅在前九个月累计装机521.08GW,同比增长达到45.3%,已成为第二大电源类型超过水电。根据《2023中国与全球光伏发展白皮书》预测,到2030年,中国能够实现国家规划的风电和光…...

逆流而上的选择-积极生活,逆流而上
首先请大家看一个故事 李明坐在公司的开放式办公区,耳边是键盘敲击声的交响乐,眼前是一行行跳跃的代码。他的眼神有些恍惚,显示器的蓝光在他眼镜上反射出时代的光芒,这光芒既耀眼又刺眼。他即将35岁,在这个年纪&#x…...

SpringMVC基础Controller
文章目录 Controller 的编写和配置1. Controller 注解类型2. RequestMapping 注解类型3. 编写请求方法4. 请求参数和路径变量 Controller 的编写和配置 Controller 注解和 RequestMapping 注解是 Spring MVC 最重要的两个注解。 使用基于注解的控制器的优点如下: …...

spark 参数
spark.yarn.executor.memoryOverhead 默认值是384M Configuration - Spark 3.5.1 Documentation...
java调用jacob进行文件转换ppt转pdf或者png
java调用jacob进行文件转换ppt转pdf或者png 前情提要 最近项目上,遇到一个复杂的ppt,最终要求是要将ppt每一页转成图片原本这个是不难,网上一搜一大堆案例,外加我本身也比较精通aspose,那还不是分分钟搞定。结果就是…...

鸿蒙HarmonyOS应用开发之使用DevEco Studio模板构建NDK工程
NDK通过CMake和Ninja编译应用的C/C代码,编译过程如下图所示。 核心编译过程如下: 根据CMake配置脚本以及build-profile.json5中配置的externalNativeOptions构建参数,与缓存中的配置比对后,生成CMake命令并执行CMake。 执行Ninja…...
uniapp流浪动物救助小程序Java宠物领养小程序springboot
uniapp流浪动物救助小程序Java宠物领养小程序springboot 代码40块,需要的私聊 前台基于uniapp小程序 后台管理基于springbootvue前后端分离项目 开发语言:Java 框架:springboot vue JDK版本:JDK1.8(或11…...
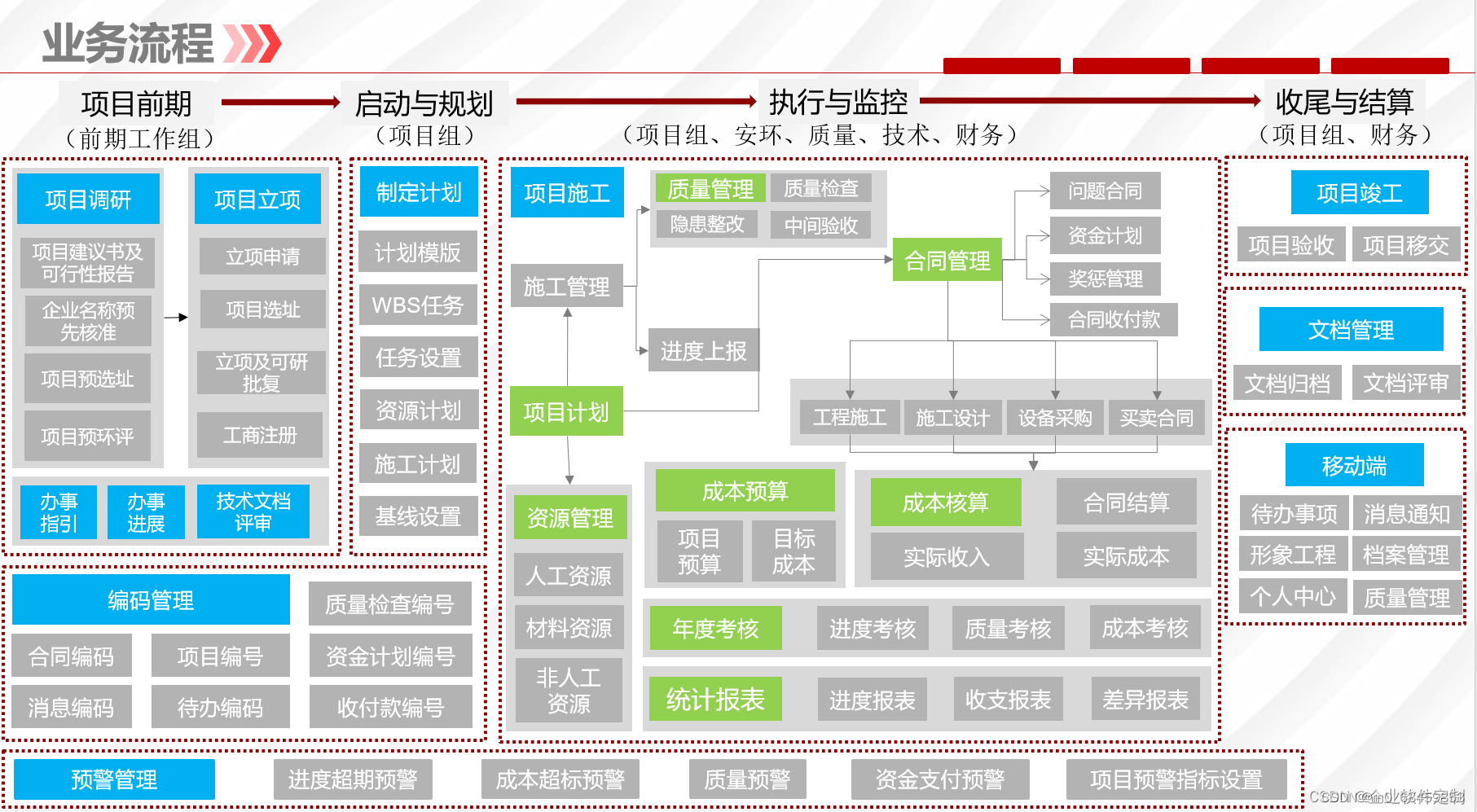
工程企业的未来选择:Java版工程项目管理系统平台与数字化管理的融合
在现代化的工程项目管理中,一套功能全面、操作便捷的系统至关重要。本文将介绍一个基于Spring Cloud和Spring Boot技术的Java版工程项目管理系统,结合Vue和ElementUI实现前后端分离。该系统涵盖了项目管理、合同管理、预警管理、竣工管理、质量管理等多个…...

Vue使用el-statistic和el-card显示大屏中的统计数据
一、页面内容: <el-row :gutter"20"><el-col :span"6"><el-card class"box-card"><div><el-statisticgroup-separator",":precision"2":value"value2":title"tit…...

12.2024
如下图所示,小明用从1开始的正整数“蛇形”填充无限大的矩阵。 1 2 6 7 15 16 28 29... 35 8 14 17 27 30... 4 9 13 18 26 31... 10 12 19 25 32... 11 20 24 33... 21 23 34.. 22 35... 容易看出矩阵第二行第二列中的数是5。请你计算矩阵中第20行第20列的数是多少…...
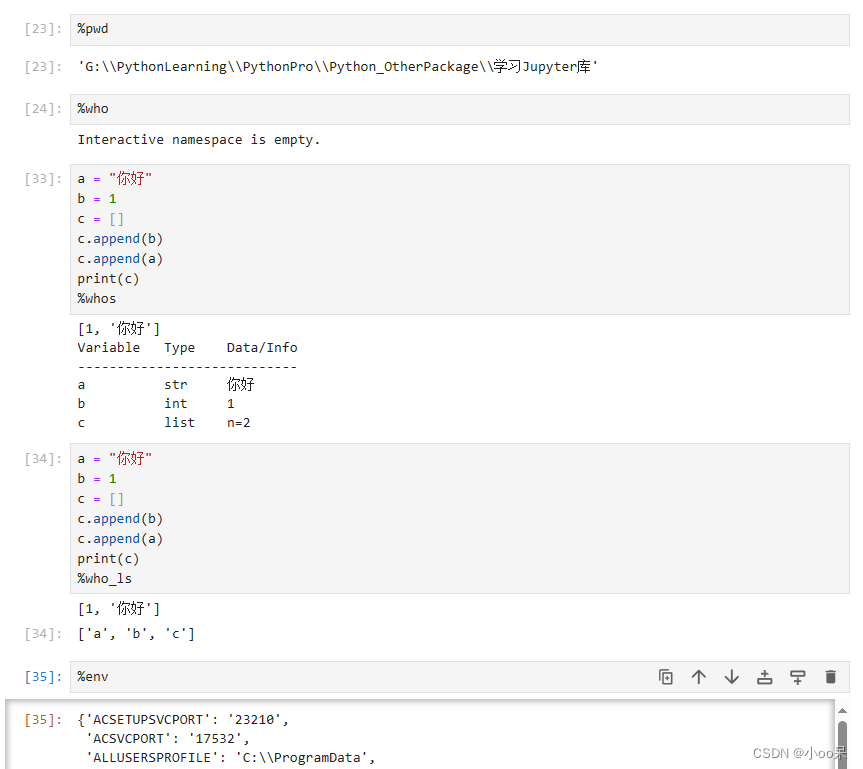
【学习心得】Jupyter常用操作与魔法方法
一、安装与打开 Jupyter是什么我就不啰嗦了,直接安装: pip install jupyter 安装完后,在你想要打开的项目路径下,唤出CMD执行下面命令就可以使用jupyter notebook了 jupyter notebook 也可以用更加好用的jupyter lab࿰…...

Linux命令别名
别名是命令的快捷方式。对于需要经常执行,并需要很长时间输入的长命令创建快捷方式很有用。 临时修改 语法: alias 别名原命令 [选项] [参数][rootdd ~]# alias cdtcd /test #切换到/test下的快捷命令 删除别名: unalias 别名 unalias cd…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

EEG-fNIRS联合成像在跨频率耦合研究中的创新应用
摘要 神经影像技术对医学科学产生了深远的影响,推动了许多神经系统疾病研究的进展并改善了其诊断方法。在此背景下,基于神经血管耦合现象的多模态神经影像方法,通过融合各自优势来提供有关大脑皮层神经活动的互补信息。在这里,本研…...
数据挖掘是什么?数据挖掘技术有哪些?
目录 一、数据挖掘是什么 二、常见的数据挖掘技术 1. 关联规则挖掘 2. 分类算法 3. 聚类分析 4. 回归分析 三、数据挖掘的应用领域 1. 商业领域 2. 医疗领域 3. 金融领域 4. 其他领域 四、数据挖掘面临的挑战和未来趋势 1. 面临的挑战 2. 未来趋势 五、总结 数据…...

中科院1区顶刊|IF14+:多组学MR联合单细胞时空分析,锁定心血管代谢疾病的免疫治疗新靶点
中科院1区顶刊|IF14:多组学MR联合单细胞时空分析,锁定心血管代谢疾病的免疫治疗新靶点 当下,免疫与代谢性疾病的关联研究已成为生命科学领域的前沿热点。随着研究的深入,我们愈发清晰地认识到免疫系统与代谢系统之间存在着极为复…...

【大厂机试题解法笔记】矩阵匹配
题目 从一个 N * M(N ≤ M)的矩阵中选出 N 个数,任意两个数字不能在同一行或同一列,求选出来的 N 个数中第 K 大的数字的最小值是多少。 输入描述 输入矩阵要求:1 ≤ K ≤ N ≤ M ≤ 150 输入格式 N M K N*M矩阵 输…...
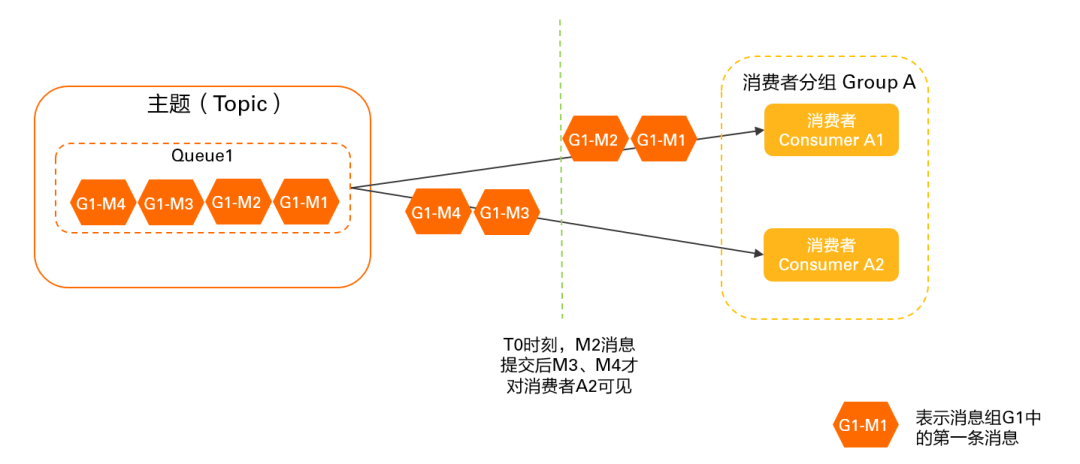
RocketMQ 客户端负载均衡机制详解及最佳实践
延伸阅读:🔍「RocketMQ 中文社区」 持续更新源码解析/最佳实践,提供 RocketMQ 专家 AI 答疑服务 前言 本文介绍 RocketMQ 负载均衡机制,主要涉及负载均衡发生的时机、客户端负载均衡对消费的影响(消息堆积/消费毛刺等…...
