【学习心得】Jupyter常用操作与魔法方法
一、安装与打开
Jupyter是什么我就不啰嗦了,直接安装:
pip install jupyter安装完后,在你想要打开的项目路径下,唤出CMD执行下面命令就可以使用jupyter notebook了
jupyter notebook![]()
也可以用更加好用的jupyter lab,它的命名如下
jupyter lab![]()
二、常用操作
(1)切换单元格编辑模式
- 进入编辑模式:
Enter - 进入命令模式:
Esc
(2)单元格类型切换
只有退出编辑模式,进入命令模式的时候才能执行单元格类型切换快捷键
- 切换到Markdown格式:
m - 切换到代码格式:
y
(3)单元格操作
- 创建新单元格(上方/下方):
A(上方)或B(下方) - 删除当前单元格:双击
D - 运行当前单元格并选中下个单元格:
Shift + Enter - 运行当前单元格并在原地生成输出:
Ctrl + Enter - 运行当前单元格并插入新单元格
Alt + Enter - 复制选中的单元格
C - 剪切选中的单元格
X - 粘贴到下方单元格
V - 查看帮助文档
Shift + Tab
(4)执行系统命令
Jupyter中用感叹号不加空格紧跟系统命令的方式,在Jupyter单元格中直接执行。
!pip install numpy比如通过这种方式就可以直接运行pip来下载安装包。
三、常见魔法方法
魔法命令是以 % 或者 %% 开头的特殊指令,用于在Jupyter Notebook中快速执行特定的任务。 一个百分号只能对一行生效,两个百分号可以对整个单元格生效。
%lsmagic:列出所有的魔法命令
(1)文件操作
%load:加载指定文件的内容到当前单元格。%run:运行指定的Python脚本文件,并将全局变量导入当前会话。%%writefile:将单元格内容写入到指定文件中。
(2)性能测试
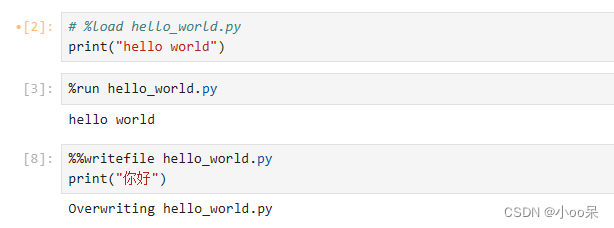
%time:测量单次代码执行时间。%timeit:多次运行代码以计算平均执行时间。-
%%time:输出整个代码块执行结束后的总耗时。 %%timeit:多次运行单元格里的代码计算平均执行时间。
(3)执行其他语言的代码
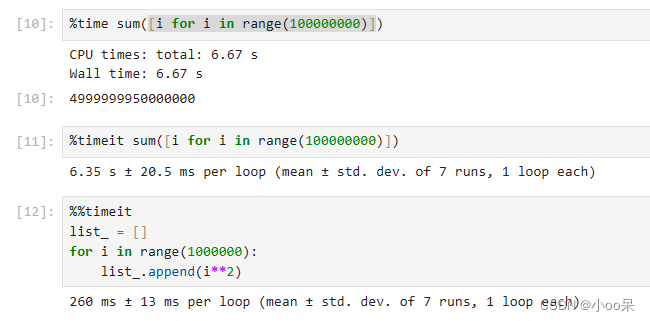
%%html:在单元格中执行HTML代码。%%javascript或%%js:执行JavaScript代码。%%latex:插入LaTeX表达式。
(4)环境与系统操作
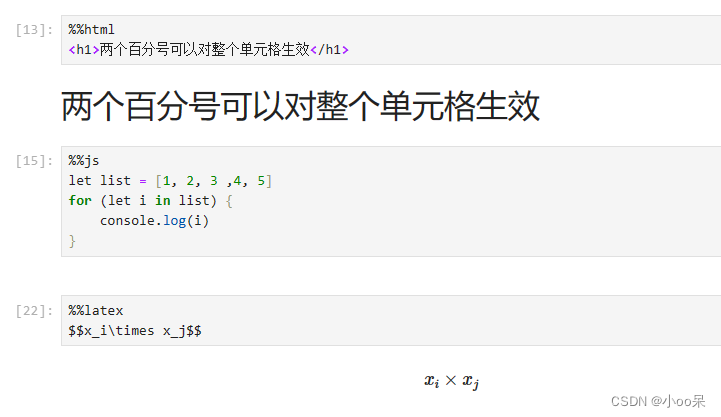
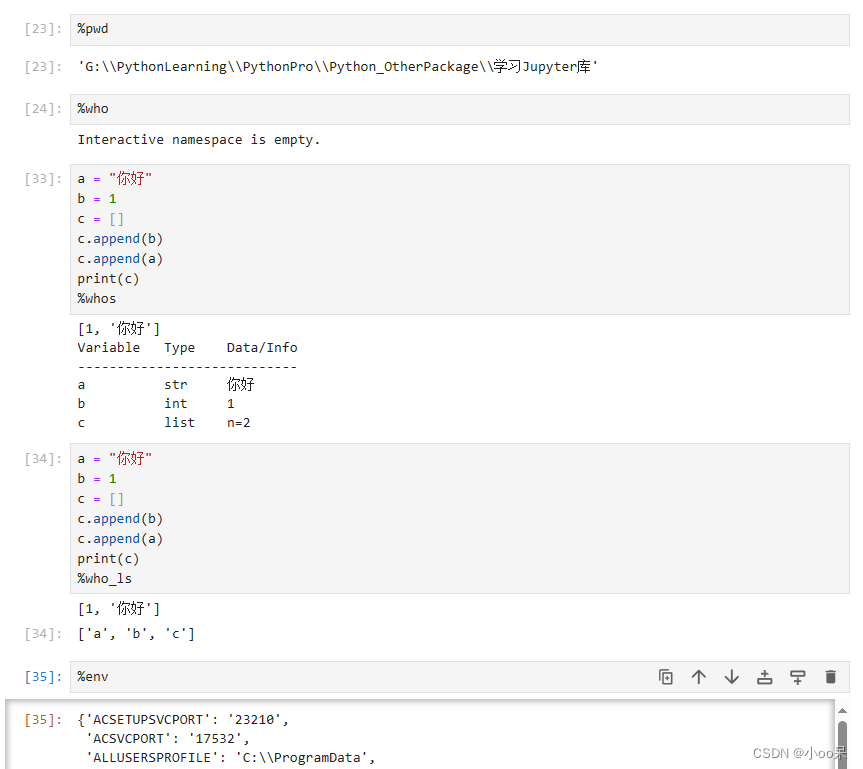
%pwd:显示当前工作目录。%who:显示当前内建作用域中定义的所有变量名。-
%whos:显示每个变量的类型以及大小等更多信息。 -
%who_ls:显示每个变量,返回列表形式。 %env查看当前环境中的环境变量。
相关文章:

【学习心得】Jupyter常用操作与魔法方法
一、安装与打开 Jupyter是什么我就不啰嗦了,直接安装: pip install jupyter 安装完后,在你想要打开的项目路径下,唤出CMD执行下面命令就可以使用jupyter notebook了 jupyter notebook 也可以用更加好用的jupyter lab࿰…...

Linux命令别名
别名是命令的快捷方式。对于需要经常执行,并需要很长时间输入的长命令创建快捷方式很有用。 临时修改 语法: alias 别名原命令 [选项] [参数][rootdd ~]# alias cdtcd /test #切换到/test下的快捷命令 删除别名: unalias 别名 unalias cd…...

Docker和 Containerd 的区别
自 Docker 开启了使用容器的爆发式增长,有越来越多的工具和标准来帮助管理和使用这项容器化技术,与此同时也造成了有很多术语让人感到困惑。 容器生态系统 容器生态系统是由许多令人兴奋的技术、大量的专业术语和大公司相互争斗组成的。 幸运的是&…...
)
Qt实现TFTP Server和 TFTP Client(二)
3 实现 3.1 Core Core模块包括下面4个类: TFTPBaseUdpTFtpClientFileTFtpServerFile 3.1.1 TFTP TFTP类实现了TFTP协议。 3.1.1.1 TFTP定义 class TFtp { public:TFtp();enum Code {RRQ 0x0001,//Read requestWRQ 0x0002,//Write requestDATA 0x0003…...
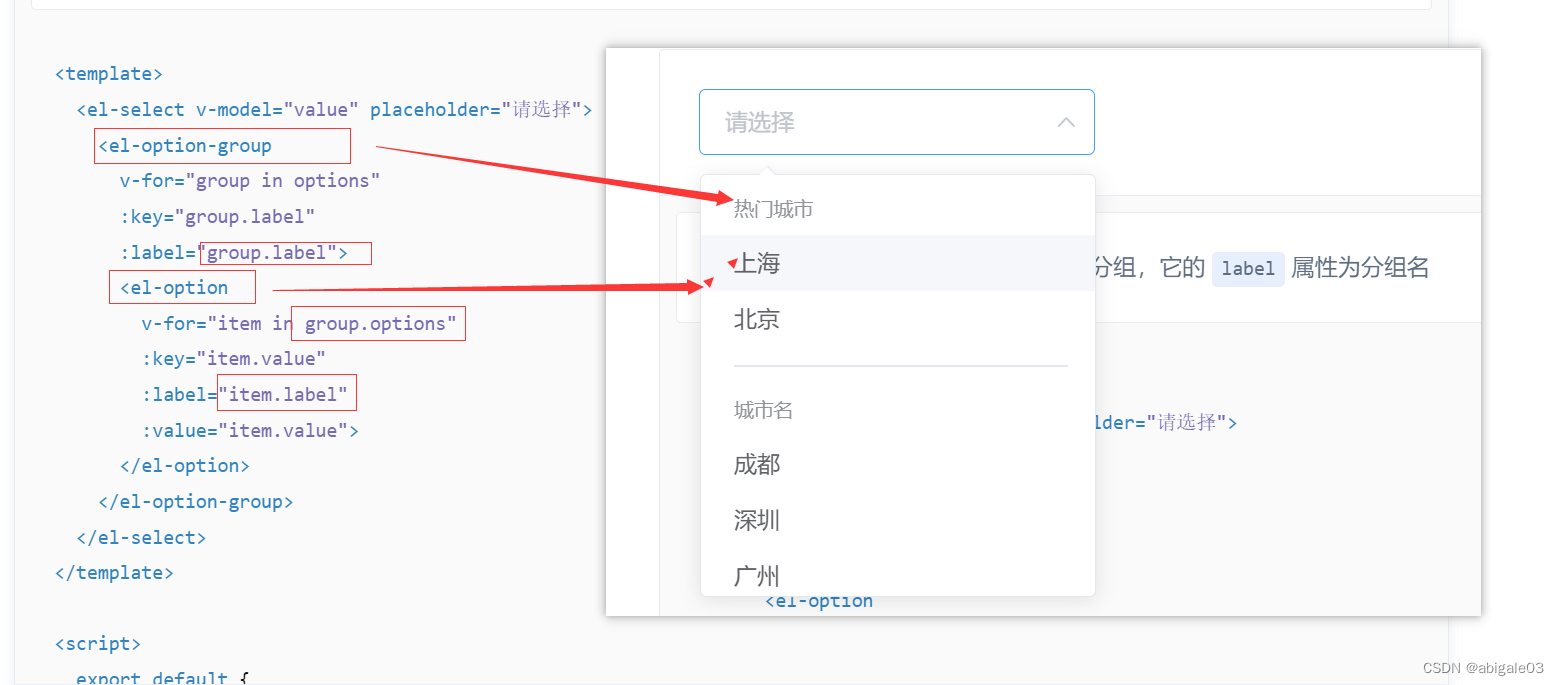
【b站李炎恢】Vue.js Element UI | 十天技能课堂 | 更新中... | 李炎恢
课程地址:【Vue.js Element UI | 十天技能课堂 | 更新中... | 李炎恢】 https://www.bilibili.com/video/BV1U54y127GB/?share_sourcecopy_web&vd_sourceb1cb921b73fe3808550eaf2224d1c155 备注:虽然标题声明还在更新中,但是看一些常用…...

AI大语言模型工程师学习路线
文章目录 运行LLMSLLM APIS开源的大语言模型Prompt engineering1. 明确目标2. 理解模型能力3. 使用示例4. 精确和具体的指令5. 考虑上下文6. 避免偏见和不准确的信息7. 测试和迭代8. 使用模板9. 考虑多语言能力10. 注意伦理和合规性结构化输出1. 使用明确的提示(Prompts)2. 采…...
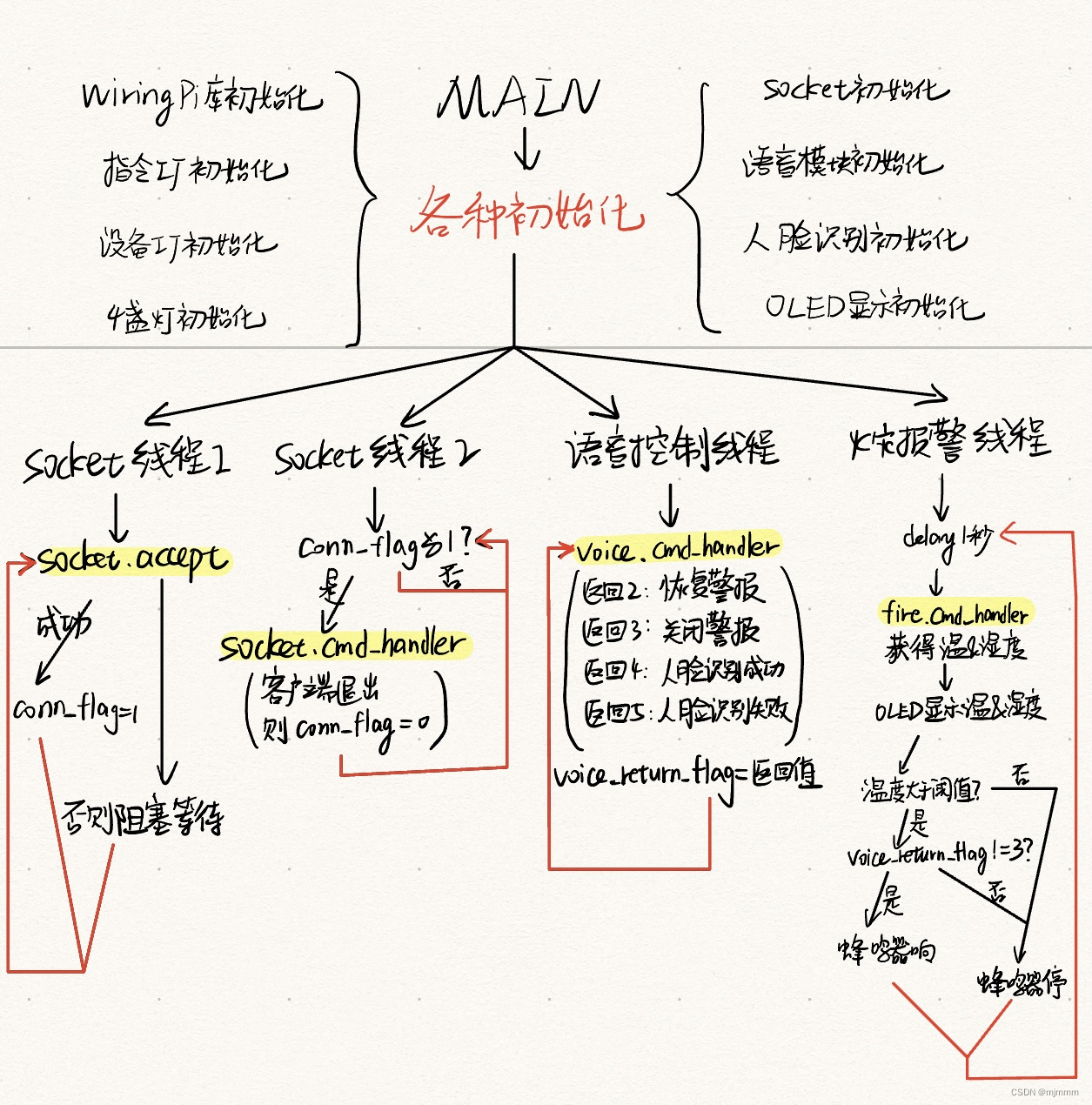
基于树莓派实现 --- 智能家居
最效果展示 演示视频链接:基于树莓派实现的智能家居_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV1Tr421n7BM/?spm_id_from333.999.0.0 (PS:房屋模型的搭建是靠纸板箱和淘宝买的家居模型,户型参考了留学时短租的公寓~&a…...
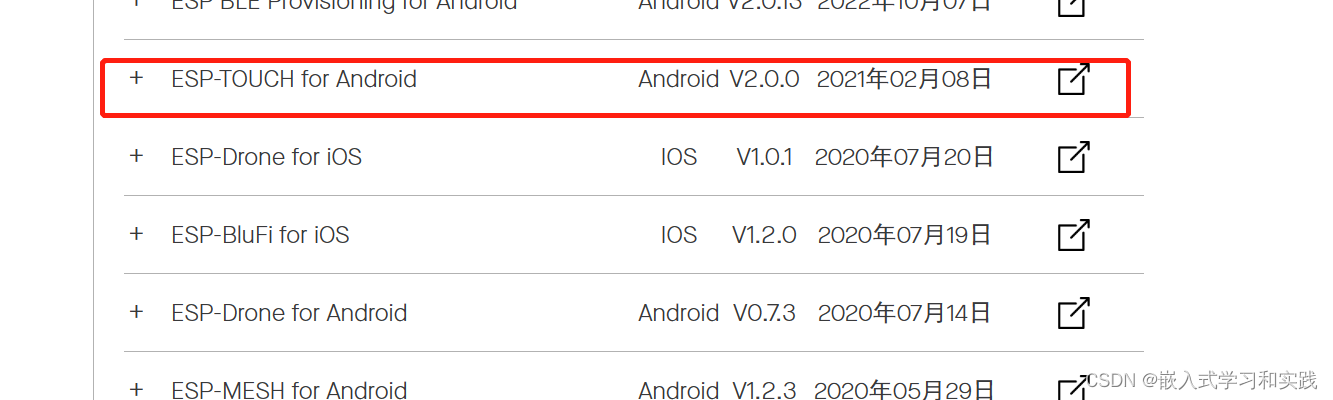
基于Arduino IDE 野火ESP8266模块 一键配网 的开发
一、配网介绍 ESP8266 一键配网(也称为 SmartConfig 或 FastConfig)是一种允许用户通过智能手机上的应用程序快速配置 ESP8266 Wi-Fi 模块的方法,而无需手动输入 SSID 和密码。为了实现这一功能,则需要一个支持 SmartConfig 的智能…...
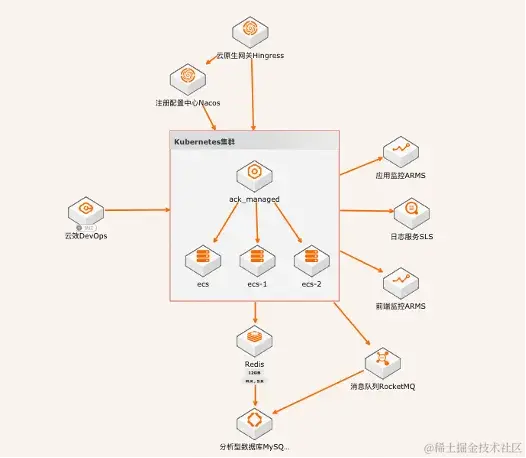
左手医生:医疗 AI 企业的云原生提效降本之路
相信这样的经历对很多人来说并不陌生:为了能到更好的医院治病,不惜路途遥远奔波到大城市;或者只是看个小病,也得排上半天长队。这些由于医疗资源分配不均导致的就医问题已是老生长谈。 云计算、人工智能、大数据等技术的发展和融…...

ceph集群部署
1. 每台服务器各增加2块硬盘(类型最好是相同的) 2. 将三台主机名设为node1.openlab.edu、node2.openlab.edu、node3.openlab.edu 3. 登录所有主机,配置 /etc/hosts 文件 192.168.136.55 ceph1.openlab.edu ceph1 192.168.136.56 ceph2.openlab.edu ceph2 192.168…...

C#WPF控件Label宽度绑定到父控件的宽度
如何将Label的宽度绑定到它所在Grid的宽度。跟随父控件的宽度的改变而改变。 <Window x:Class="WpfApp.MainWindow"xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation"xmlns:x="http://schemas.microsoft.com/winfx/2006/xaml&q…...

HMI的学习
什么是HMI?了解HMI或人机界面的一些基础知识_哔哩哔哩_bilibili Human Machine Interface 人机界面 在工业中使用HMI来控制和监视设备 常见的HMI是ATM机 通过屏幕和按钮来完成取款或存款 工业中,操作员或维护人员可以从HMI操作和监视设备。 它们可能…...

工业无线网关在汽车制造企业的应用效果和价值-天拓四方
随着智能制造的快速发展,工业无线网关作为关键通信设备,在提升生产效率、优化生产流程、实现设备间的互联互通等方面发挥着越来越重要的作用。以下是一个关于工业无线网关在智能制造行业应用的具体案例,展示了其在实际生产中的应用效果和价值…...
校园app开发流程-uniapp开发-支持APP小程序H5-源码交付-跑腿-二手市场-交友论坛等功能,学校自由选择!
随着科技的不断发展,智慧校园系统和跑腿外卖小程序已经成为当今社会的热门话题。作为未来的重要趋势之一,科技在教育领域中的应用越来越广泛。本文将探讨智慧校园系统和跑腿外卖小程序的开发过程,并阐述如何利用科技“育”见未来 一、智慧校…...
Machine Learning机器学习之K近邻算法(K-Nearest Neighbors,KNN)
目录 前言 背景介绍: 思想: 原理: KNN算法关键问题 一、构建KNN算法 总结: 博主介绍:✌专注于前后端、机器学习、人工智能应用领域开发的优质创作者、秉着互联网精神开源贡献精神,答疑解惑、坚持优质作品共…...

四、在数据库里建库
一、查库 ##1)库:一个库就是一个excell文档,库里含有表,一个表就是一个excell的sheet. ##2)查看数据库实例中有哪些库 MariaDB [(none)]> show databases; -------------------- | Database | -------------------- | informat…...

蓝桥杯-网络安全比赛(2)基础学习-正则表达式匹配电话号码、HTTP网址、IP地址、密码校验
正则表达式(Regular Expression):定义:一种强大的文本处理工具,用于描述、匹配和查找字符串中的特定模式。应用:密码验证、文本搜索和替换、数据清洗等。特点:通过特定的元字符和规则来构建复杂…...

如何创建azure pipeline
Azure Pipelines是一种持续集成和持续交付(CI/CD)工具,可以帮助开发团队自动化构建、测试和部署应用程序。以下是创建Azure Pipeline的步骤: 登录到Azure DevOps(https://dev.azure.com/)。在Azure DevOps…...

缓存菜品、套餐、购物车相关功能
一、缓存菜品 通过缓存的方式提高查询性能 1.1问题说明 大量的用户访问导致数据库访问压力增大,造成系统响应慢,用户体验差 1.2 实现思路 优先查询缓存,如果缓存没有再去查询数据库,然后载入缓存 将菜品集合序列化后缓存入red…...

微信小程序的页面交互1
一、page()函数 每个页面的s代码全部写入对应的js文件的page()函数里面。点击编译,就可以显示js代码的运行效果。注意,每个页面的page()函数是唯一的。 page(ÿ…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...

xmind转换为markdown
文章目录 解锁思维导图新姿势:将XMind转为结构化Markdown 一、认识Xmind结构二、核心转换流程详解1.解压XMind文件(ZIP处理)2.解析JSON数据结构3:递归转换树形结构4:Markdown层级生成逻辑 三、完整代码 解锁思维导图新…...

Windows 下端口占用排查与释放全攻略
Windows 下端口占用排查与释放全攻略 在开发和运维过程中,经常会遇到端口被占用的问题(如 8080、3306 等常用端口)。本文将详细介绍如何通过命令行和图形化界面快速定位并释放被占用的端口,帮助你高效解决此类问题。 一、准…...

云原生安全实战:API网关Envoy的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关 作为微服务架构的统一入口,负责路由转发、安全控制、流量管理等核心功能。 2. Envoy 由Lyft开源的高性能云原生…...
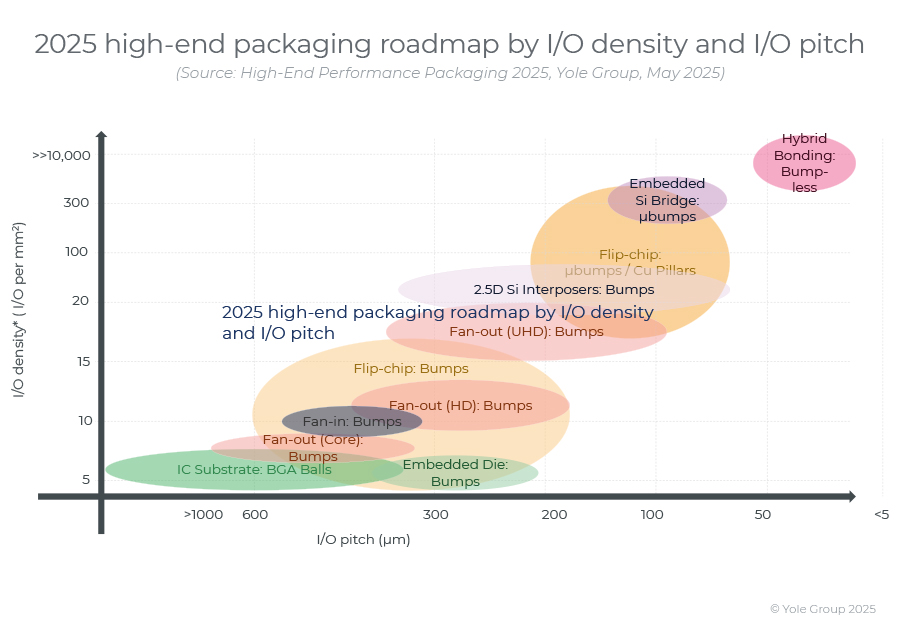
高端性能封装正在突破性能壁垒,其芯片集成技术助力人工智能革命。
2024 年,高端封装市场规模为 80 亿美元,预计到 2030 年将超过 280 亿美元,2024-2030 年复合年增长率为 23%。 细分到各个终端市场,最大的高端性能封装市场是“电信和基础设施”,2024 年该市场创造了超过 67% 的收入。…...

用鸿蒙HarmonyOS5实现国际象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的国际象棋小游戏的完整实现代码,使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├── …...
)
window 显示驱动开发-如何查询视频处理功能(三)
D3DDDICAPS_GETPROCAMPRANGE请求类型 UMD 返回指向 DXVADDI_VALUERANGE 结构的指针,该结构包含特定视频流上特定 ProcAmp 控件属性允许的值范围。 Direct3D 运行时在D3DDDIARG_GETCAPS的 pInfo 成员指向的变量中为特定视频流的 ProcAmp 控件属性指定DXVADDI_QUER…...
