数据结构——排序算法
1、排序的概念
排序是指的是将一组数据(如数字、单词、记录等)按照某种特定的顺序(升序或降序)进行排列的过程。排序算法是实现排序的程序或方法,它们在软件开发和数据处理中扮演着至关重要的角色。
排序算法可以根据不同的标准进行分类,如:
-
内部排序与外部排序:内部排序是指数据全部加载到内存中进行排序,而外部排序则涉及处理大量数据,这些数据可能太大而无法一次性放入内存。
-
比较排序与非比较排序:比较排序是基于比较操作来决定元素之间的相对顺序,如快速排序、归并排序等。非比较排序不通过比较来确定元素的顺序,如计数排序、基数排序等。
-
稳定性:稳定的排序算法能够保持相等元素的原始顺序,而非稳定排序算法可能会改变相等元素的顺序。
-
时间复杂度:算法执行所需的时间与输入数据量的关系。常见的时间复杂度有O(n)、O(n log n)、O(n^2)等。
-
空间复杂度:算法执行过程中需要的额外空间量。
-
在线排序与离线排序:在线排序是指数据一个接一个地处理,而离线排序则是在所有数据都可用的情况下进行。
2、常见的排序算法
接下来我们一一实现:
直接插入排序
void InsertSort(int* a, int n)
{for (int i = 0; i < n - 1; i++){int end = i;int tem = a[end + 1];while (end >= 0){if (tem < a[end]){a[end + 1] = a[end];end--;}elsebreak;}a[end + 1] = tem;}
}排序思想是认为第一个元素是有序的,然后从第二个元素开始排序,先把元素保存到tem中,然后从后往前遍历数组,找到比tem大的就向后挪一位,遍历完后把tem放到下标为ennd+1的位置上,继续排下一个数
看一下动图演示:

直接插入排序的
时间复杂度:O(N^2)
空间复杂度:O(1)
稳定性:稳定
希尔排序
void ShellSort(int* a, int n)
{int gap = n;while (gap > 1){gap = gap / 2;for (int i = 0; i < n - gap; i++){int end = i;int tem = a[end + gap];while (end >= 0){if (tem < a[end]){a[end + gap] = a[end];end -= gap;}elsebreak;}a[end + gap] = tem;}}
}希尔排序(Shell Sort)是插入排序的一种更高效的改进版本,由Donald Shell于1959年提出。它是基于插入排序的一种分组比较排序算法,也被称为“缩小增量排序”。希尔排序的核心思想是将原始数据集分割成若干个子序列进行插入排序,这些子序列由原始数据集中的元素按照增量序列划分而来。随着增量序列的减小,整个数据集逐渐被整合成一个有序的序列。
动图演示:

-
选择增量序列:增量序列的选择对希尔排序的性能有很大影响。常见的增量序列有希尔原始序列(N/2,N/4,...,1),Hibbard增量序列(1, 3, 7, ..., 2^k - 1),Knuth序列(1, 4, 13, ..., (3^k - 1)/2)等。
-
分组:按照当前增量将数组分为若干子序列。例如,如果当前增量是5,那么索引为0, 5, 10, ...的元素将分为一组,索引为1, 6, 11, ...的元素将分为另一组,以此类推。
-
对各组进行插入排序:在每个子序列上应用插入排序算法,使得每个子序列有序。
-
减小增量,重复上述步骤:随着增量的减小,子序列的间隔逐渐减小,最终当增量为1时,整个数组将作为一个序列进行一次插入排序,此时数组应该是基本有序的,所以最后一步的插入排序会非常快。
-
完成排序:当增量减小到1时,整个数组将作为一个序列进行最后一次插入排序,此时数组已经基本有序,所以排序会很快完成。
时间复杂度:希尔排序的时间复杂度依赖于增量序列的选择。最坏情况下的时间复杂度为O(n^2),但是对于中等大小的数组,实际运行时间可能接近于O(n log^2 n)。最佳情况下,如果增量序列选择得当,时间复杂度可以达到O(n log n)。 有人算出希尔排序的时间复杂度接近于O(N^1.3),我们记住就行了。
空间复杂度:O(1)
稳定性:不稳定
选择排序
void SelectSort(int* a, int n)
{int begin = 0, end = n - 1;while (begin < end){int mini = begin, maxi = begin;for (int i = begin + 1; i <= end; i++){if (a[i] < a[mini])mini = i;if (a[i] > a[maxi])maxi = i;}swap(&a[begin], &a[mini]);if (maxi == begin)maxi = mini;swap(&a[end], &a[maxi]);begin++;end--;}
}选择排序(Selection Sort)是一种简单直观的排序算法。它的工作原理是每次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完。
上面是对选择排序的优化,同时选取最大和最小的值进行比较,然后放在队头和队尾
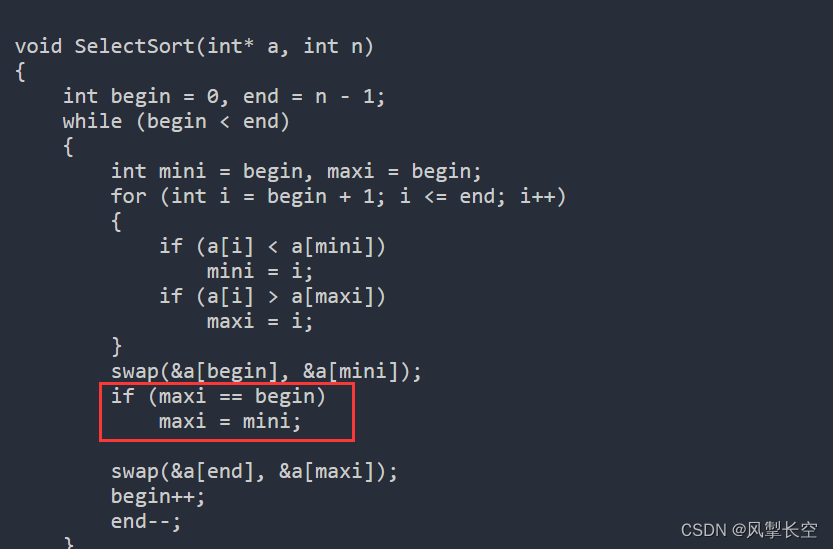
if语句是为了当前数组中最大的数在最小的位置上,会发生重复交换,如果加个if语句可以避免这种情况,如果不理解的小伙伴可以把if语句去掉,调试一下去发现问题,肯定会理解的更加透彻!
冒泡排序
代码展示:
//冒泡排序
void bubblesort(int* a, int n)
{for (int i = 0; i < n - 1; i++){for (int j = 0; j < n - 1 - i; j++){if (a[j + 1] < a[j]){swap(&a[j + 1], &a[j]);}}}
}冒泡排序(Bubble Sort)是一种简单的排序算法。它重复地遍历要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来。遍历数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。
冒泡排序的基本思想是:通过相邻元素之间的比较和交换,每一轮比较后,最大的元素会“冒泡”到数列的最后位置。这个过程会重复进行,直到整个数列有序。
时间复杂度:O(N^2)
空间复杂度:O(1)
稳定性:稳定
堆排序
void AdjustDown(int* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n){if (child + 1 < n && a[child + 1] > a[child]){child++;}if (a[child] > a[parent]){swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}}
//堆排序 排升序
void heapsort(int* a, int n)
{for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(a, n, i);}int end = n - 1;while (end >= 0){swap(&a[0], &a[end]);AdjustDown(a, end, 0);end--;}
}堆排序使用了二叉树的思想,用向下调整建堆,如果我们建的是小堆,然后交换堆顶和堆最后一个元素,这样最小的元素就到了最后,然后依次向下调整,就形成了升序,
快速排序
快速排序(Quick Sort)是一种高效的排序算法,由C. A. R. Hoare在1960年提出。它的基本思想是通过一趟排序将待排记录分隔成独立的两部分,其中一部分的所有记录的关键字均比另一部分的关键字小,然后分别对这两部分记录继续进行排序,以达到整个序列有序的目的。快速排序的核心是分治法(Divide and Conquer)策略。
void QuickSortHoare(int* a, int left, int right)
{if (left >= right)return;int begin = left, end = right;int keyi = left;while (left < right){while (left<right && a[right]>=a[keyi])right--;while (left < right && a[left] <= a[keyi])left++;swap(&a[left], &a[right]);}swap(&a[keyi], &a[left]);keyi = left;QuickSortHoare(a, begin, keyi - 1);QuickSortHoare(a, keyi+1, end);
}快速排序还有改进的双指针法:
//快速排序 双指针版本
void QuickSortTowPorters(int* a, int left, int right)
{if (left >= right)return;int keyi = left;int prev = left;int cur = left + 1;while (cur <= right){if (a[cur] < a[keyi] && ++prev != cur)swap(&a[prev], &a[cur]);cur++;}swap(&a[keyi], &a[prev]);keyi = prev;QuickSortTowPorters(a, left, keyi - 1);QuickSortTowPorters(a, keyi+1, right);
}这段代码是比较精简的,请看动图演示

归并排序
//归并排序
void _mergeSort(int* a, int begin, int end, int* tem)
{if (begin == end)return;int mid = (begin + end) / 2;_mergeSort(a, begin, mid, tem);_mergeSort(a, mid + 1, end, tem);int begin1 = begin, end1 = mid;int begin2 = mid + 1, end2 = end;int i = begin;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2])tem[i++] = a[begin1++];elsetem[i++] = a[begin2++];}while (begin1 <= end1){tem[i++] = a[begin1++];}while (begin2 <= end2){tem[i++] = a[begin2++];}memcpy(a + begin, tem + begin, sizeof(int) * (end - begin + 1));
}void MergeSort(int* a, int n)
{int* tem = (int*)malloc(sizeof(int) * n);assert(tem);_mergeSort(a, 0, n - 1, tem);free(tem);tem = NULL;
}归并排序(Merge Sort)是一种分治算法,其核心思想是将一个大问题分解成若干个较小的子问题来解决,然后将子问题的解合并起来得到原问题的解。在排序领域,归并排序通过不断地将数组分成两半,对每一半进行排序,然后将排序好的两半合并在一起,从而达到整个数组有序的目的。
归并排序的步骤可以分为两个主要部分:分裂(Divide)和合并(Merge)。
-
分裂(Divide):
- 将数组从中间分成两个相等(或接近相等)的子数组。
- 对这两个子数组分别进行归并排序。
- 这个过程会递归进行,直到子数组的长度为1,此时子数组自然是有序的。
-
合并(Merge):
- 将两个有序的子数组合并成一个更大的有序数组。
- 合并过程中,需要一个临时数组来存放合并后的有序数组。
- 比较两个子数组的前端元素,将较小的元素放入临时数组,然后移动对应的指针。
- 重复这个过程,直到所有元素都被合并到临时数组中。
- 将临时数组的内容复制回原数组(或者直接使用临时数组作为结果)。
以下是归并排序的非递归实现,比较难理解
//归并排序 非递归实现
void MergeSortNonR(int* a, int n)
{int* tem = (int*)malloc(sizeof(int) * n);assert(tem);int gap = 1;while (gap < n){for (int j = 0; j < n; j += 2 * gap){//重点,难点int begin1 = j, end1 = begin1 + gap - 1;int begin2 = begin1 + gap, end2 = begin2 + gap - 1;//处理越界问题if (begin1 > n || begin2 > n)break;if (end2 > n)end2 = n - 1;int i = j;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2])tem[i++] = a[begin1++];elsetem[i++] = a[begin2++];}while (begin1 <= end1){tem[i++] = a[begin1++];}while (begin2 <= end2){tem[i++] = a[begin2++];}memcpy(a + j, tem + j, sizeof(int) *(end2-j+1));}}
}可以看一下动图展示:
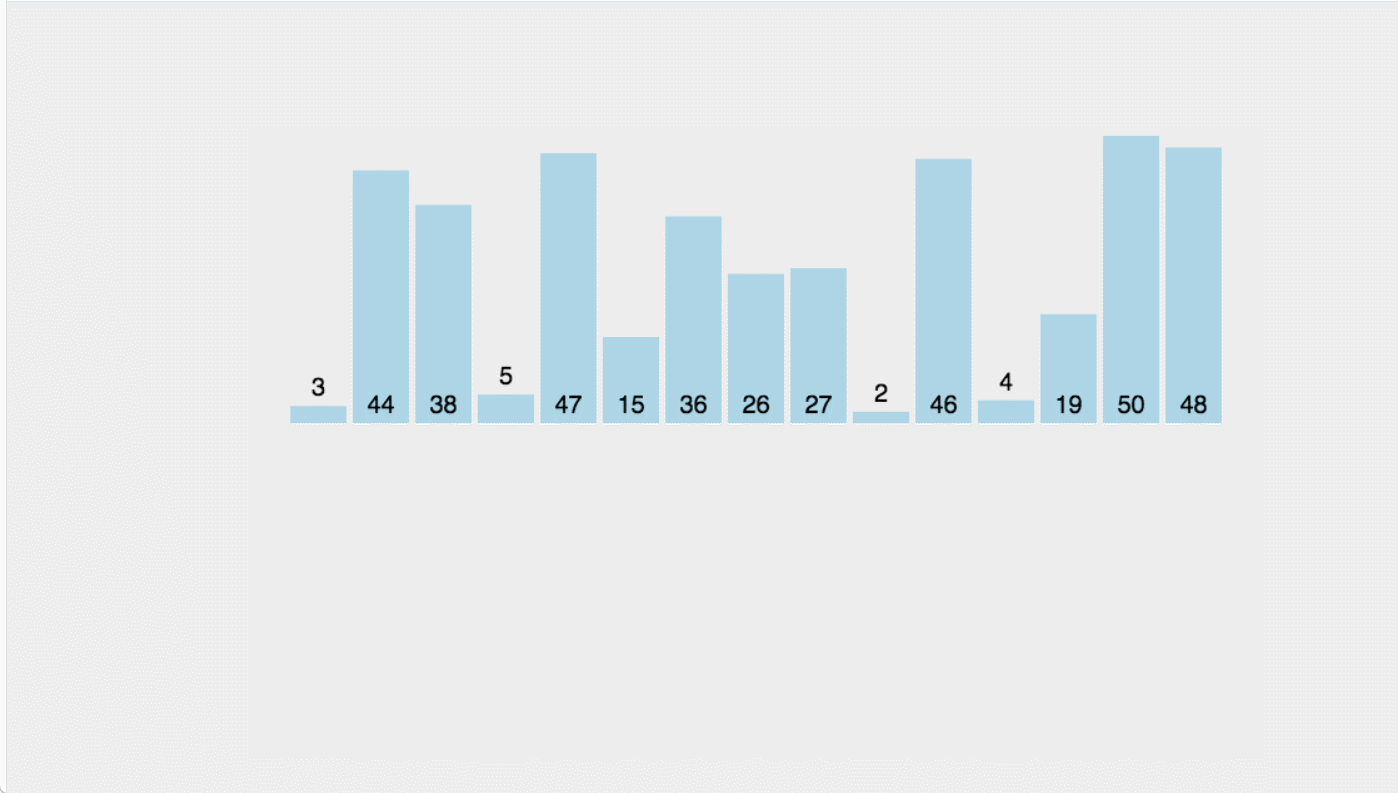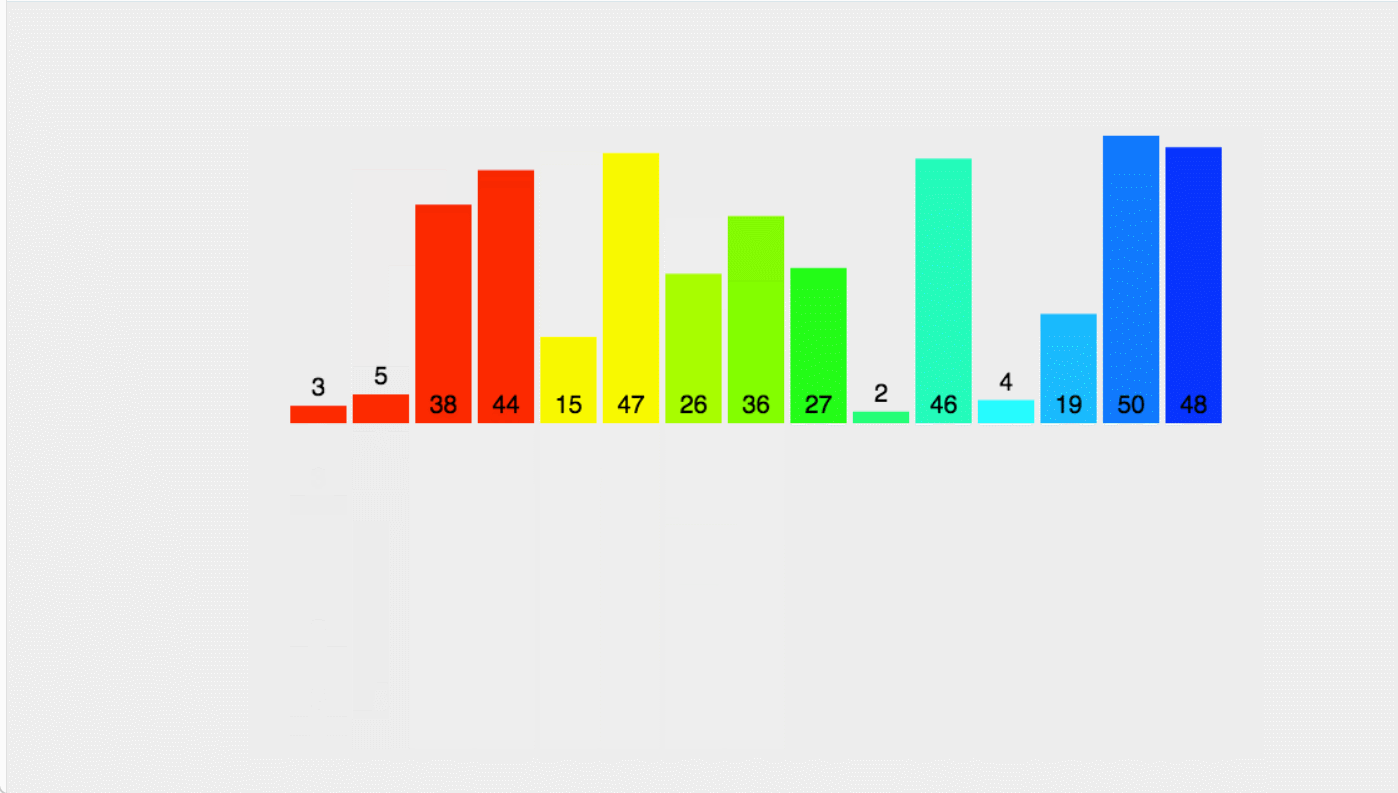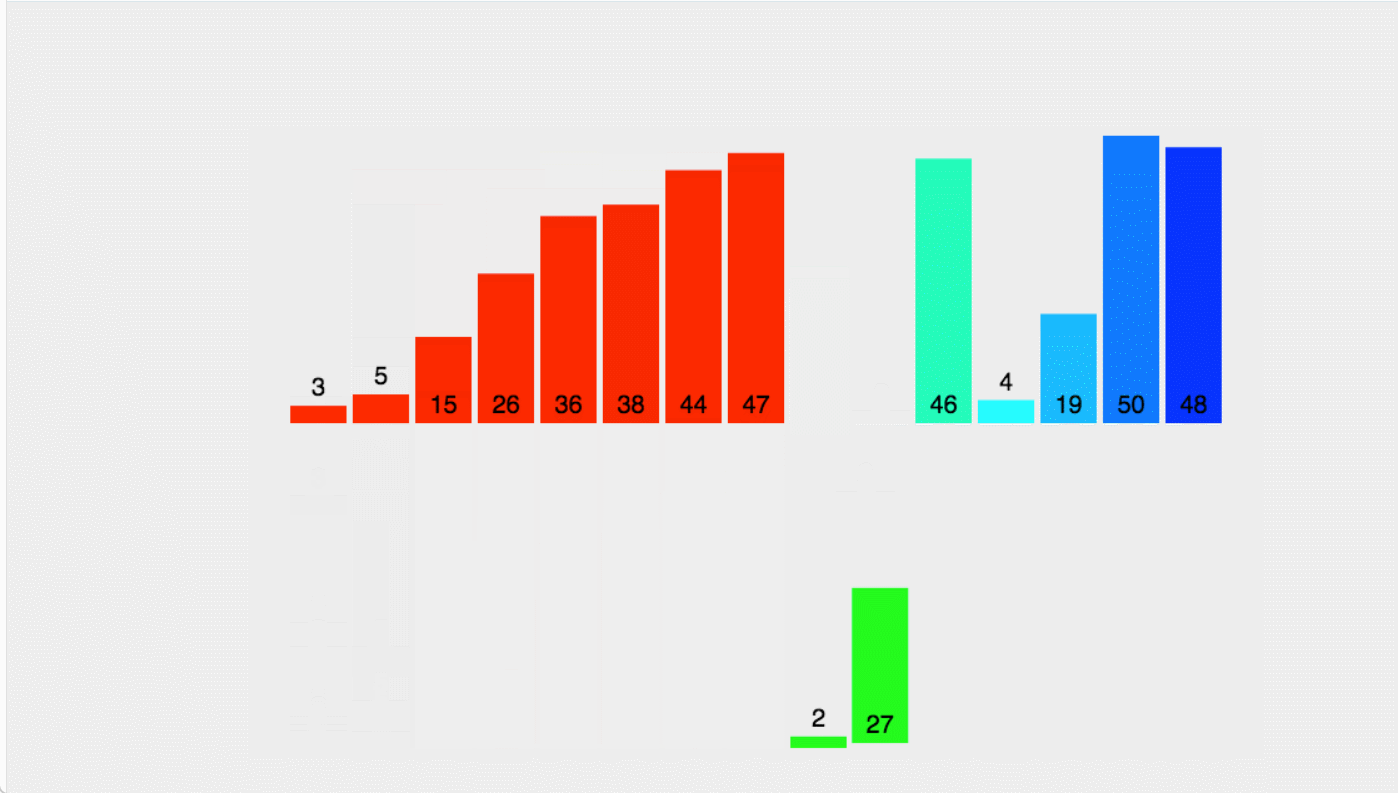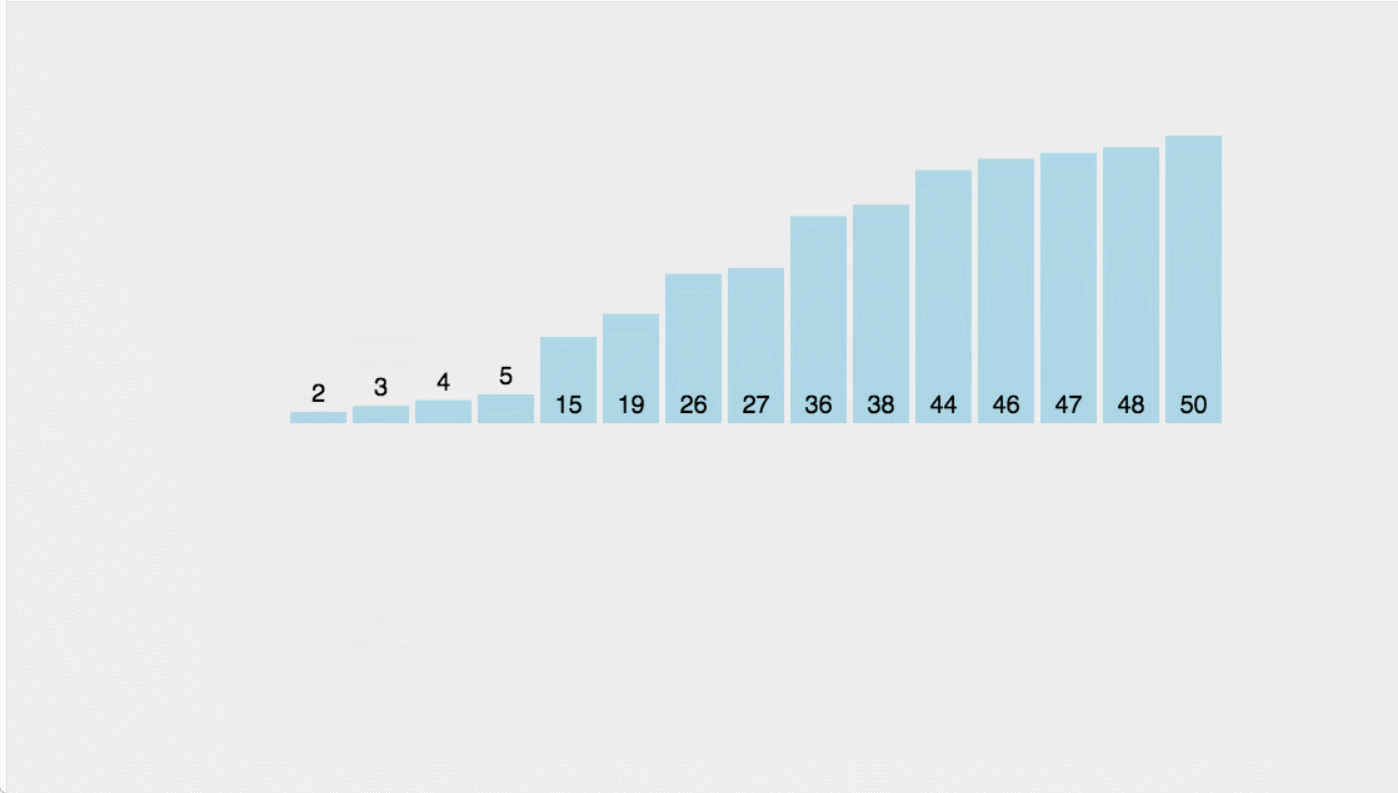
归并排序的总时间复杂度是O(n log n)。这意味着归并排序在最好、最坏和平均情况下都有相同的时间复杂度,即O(n log n)。这使得归并排序在处理大数据集时非常可靠和高效。
需要注意的是,归并排序的空间复杂度也是O(n),因为它需要一个与输入数组大小相同的临时数组来存储合并的结果。在实际应用中,归并排序的常数因子较大,因此在小数组上的排序性能可能不如其他简单排序算法,如插入排序。然而,对于大型数据集,归并排序的优势就非常明显了。
制作不易,希望对你有帮助,大家一起加油!
相关文章:

数据结构——排序算法
1、排序的概念 排序是指的是将一组数据(如数字、单词、记录等)按照某种特定的顺序(升序或降序)进行排列的过程。排序算法是实现排序的程序或方法,它们在软件开发和数据处理中扮演着至关重要的角色。 排序算法可以根据…...

MyBatis的高级特性探索
MyBatis 是一个流行的Java持久层框架,它提供了简单和直观的方法来处理数据库操作。相比于传统的JDBC操作,MyBatis通过XML或注解方式映射Java对象与数据库之间的关系,极大地简化了数据库编程工作。除了基本的数据映射和SQL语句执行功能&#x…...

未来制造:机器人行业新质生产力提升策略
机器人行业新质生产力提升咨询方案 一、机器人行业目前发展现状及特点: 创新活跃、应用广泛、成长性强。 二、机器人企业发展新质生产力面临的痛点: 1、高端人才匮乏 2、核心技术受限 3、竞争日益国际化 4、成本控制挑战 5、用户体验提升需求 三…...

开发过程中PostgreSQL常用的SQL语句,持续更新ing
修改字段类型 -- ALTER TABLE 模式名.表明 ALTER COLUMN 字段名 TYPE 类型; alter table alarm.alarm_produce_config alter column alarm_level type int4;重置序列值 -- ALTER SEQUENCE 序列名 RESTART WITH 序列值; alter sequence enterprise_type_id_seq restart with 1…...
)
Linux screen命令教程:如何在一个终端窗口中管理多个会话(附实例详解和注意事项)
Linux screen命令介绍 screen是一个全屏窗口管理器,它将物理终端抽象为多个虚拟终端,每个虚拟终端都可以运行一个shell或程序。screen命令可以让你在一个终端窗口中打开多个会话,每个会话都有自己的环境,可以独立运行命令。这对于…...

Android中的本地广播与全局广播
文章目录 1. 概念介绍2. 本地广播3. 全局广播 1. 概念介绍 前文我们介绍了Android中的广播,按注册方式分为静态广播和动态广播;按接收顺序分为有序广播与无序广播 本文我们按照广播的传播范围,将广播分为本地广播和全局广播 本地广播&#x…...

Debezium日常分享系列之:Debezium2.5稳定版本之MySQL连接器配置示例和Connector参数详解
Debezium日常分享系列之:Debezium2.5稳定版本之MySQL连接器配置示例和Connector参数详解 一、MySQL 连接器配置示例二、添加连接器配置三、连接器属性四、必须的连接器配置属性五、高级 MySQL 连接器配置属性六、Debezium 连接器数据库架构历史配置属性七、用于配置…...

vue3父组件给子组件传值,并在子组件接受
1、在父组件中定义数据: 在父组件中定义需要传递给子组件的数据。 <template><div><ChildComponent :message"parentMessage" /></div> </template><script> import { defineComponent } from vue; import ChildCom…...
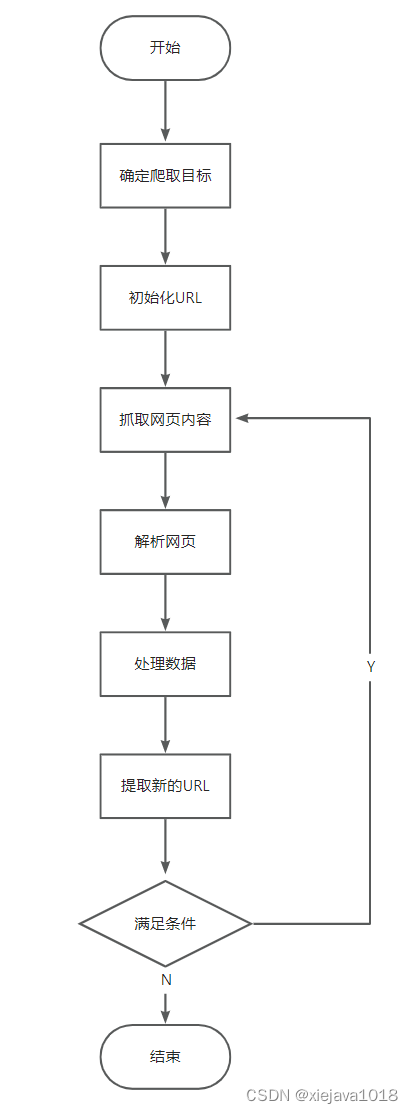
Python爬虫如何快速入门
写了几篇网络爬虫的博文后,有网友留言问Python爬虫如何入门?今天就来了解一下什么是爬虫,如何快速的上手Python爬虫。 一、什么是网络爬虫 网络爬虫,英文名称为Web Crawler或Spider,是一种通过程序在互联网上自动获取…...
酷开科技依托酷开系统用“平台+产品+场景”塑造全屋智能生活!
杰弗里摩尔的“鸿沟理论”中写道:高科技企业推进产品的早期市场和产品被广泛接受的主流市场之间,存在着一条巨大的“鸿沟”。“鸿沟”,指产品吸引早期接纳者后、赢得更多客户前的那段间歇,以及其中可预知和不可预知的阻碍。多数产…...

P8649 [蓝桥杯 2017 省 B] k 倍区间:做题笔记
目录 思路 代码思路 代码 推荐 P8649 [蓝桥杯 2017 省 B] k 倍区间 思路 额嗯,这道题我刚上来是想到了前缀和,但是还要判断每个子序列,我就两层for嵌套,暴力解了题。就是我知道暴力肯定过不了但是写不出来其他的[留下了苦…...
LeetCode题练习与总结:旋转图像
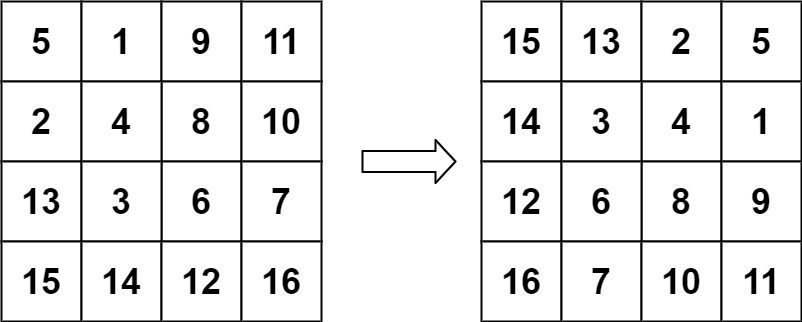
一、题目描述 给定一个 n n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。 你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。 示例 1: 输入:matrix [[1,2,3],[4,5,6],…...

如何在家中使用手机平板电脑 公司iStoreOS软路由实现远程桌面
文章目录 简介一、配置远程桌面公网地址二、家中使用永久固定地址 访问公司电脑**具体操作方法是:** 简介 软路由是PC的硬件加上路由系统来实现路由器的功能,也可以说是使用软件达成路由功能的路由器。 使用软路由控制局域网内计算机的好处:…...

【文献分享】myMUSCLE, a New Multiphysics, Multiscale Simulation Coupling Environment
题目:myMUSCLE, a New Multiphysics, Multiscale Simulation Coupling Environment 链接: https://doi.org/10.1080/00295639.2022.2148809 myMUSCLE,一种新的多物理场、多尺度仿真耦合环境 摘要 计算能力的提高使核界能够结合有关反应…...

2024年云计算使用报告,89%组织用多云,25%广泛使用生成式AI,45%需要跨云数据集成,节省成本是云首要因素
备注:本文来自Flexera2024年的云现状调研报告的翻译。原报告地址: https://info.flexera.com/CM-REPORT-State-of-the-Cloud Flexera是一家专注于做SaaS的IT解决方案公司,有30年发展历史,5万名客户,1300名员工。Flex…...

【Python操作基础】——序列
🍉CSDN小墨&晓末:https://blog.csdn.net/jd1813346972 个人介绍: 研一|统计学|干货分享 擅长Python、Matlab、R等主流编程软件 累计十余项国家级比赛奖项,参与研究经费10w、40w级横向 文…...

Vue 与 React:前端框架对比分析
🤍 前端开发工程师、技术日更博主、已过CET6 🍨 阿珊和她的猫_CSDN博客专家、23年度博客之星前端领域TOP1 🕠 牛客高级专题作者、打造专栏《前端面试必备》 、《2024面试高频手撕题》 🍚 蓝桥云课签约作者、上架课程《Vue.js 和 E…...
解决kubesphere流水线docker登陆错误http: server gave HTTP response to HTTPS client
kubesphere DevOps流水线中,在登录私有的harbor仓库时,报以下错误 docker login 111.230.19.120:80 -u admin -p test123. WARNING! Using --password via the CLI is insecure. Use --password-stdin. Error response from daemon: Get "https://…...
)
macOS安装mongoDB(homebrew)
使用 Homebrew Homebrew 是 macOS 的一个包管理器,可以非常方便地安装 MongoDB 和其他软件。如果你还没有安装 Homebrew,可以从它的官网上找到安装指令。 已安装 Homebrew的话,先更新一下homebrew brew update 你可以使用下面的命令来安装…...
免费SSL证书和付费SSL证书的区别点
背景: 在了解免费SSL证书和付费SSL证书的区别之前,先带大家了解一下SSL证书的概念和作用。 SSL证书的概念: SSL证书就是基于http超文本传输协议的延伸,在http访问的基础上增加了一个文本传输加密的协议,由于http是明…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...
实现跳一跳小游戏)
鸿蒙(HarmonyOS5)实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架,实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...

嵌入式学习之系统编程(九)OSI模型、TCP/IP模型、UDP协议网络相关编程(6.3)
目录 一、网络编程--OSI模型 二、网络编程--TCP/IP模型 三、网络接口 四、UDP网络相关编程及主要函数 编辑编辑 UDP的特征 socke函数 bind函数 recvfrom函数(接收函数) sendto函数(发送函数) 五、网络编程之 UDP 用…...

云安全与网络安全:核心区别与协同作用解析
在数字化转型的浪潮中,云安全与网络安全作为信息安全的两大支柱,常被混淆但本质不同。本文将从概念、责任分工、技术手段、威胁类型等维度深入解析两者的差异,并探讨它们的协同作用。 一、核心区别 定义与范围 网络安全:聚焦于保…...

echarts使用graphic强行给图增加一个边框(边框根据自己的图形大小设置)- 适用于无法使用dom的样式
pdf-lib https://blog.csdn.net/Shi_haoliu/article/details/148157624?spm1001.2014.3001.5501 为了完成在pdf中导出echarts图,如果边框加在dom上面,pdf-lib导出svg的时候并不会导出边框,所以只能在echarts图上面加边框 grid的边框是在图里…...

接口 RESTful 中的超媒体:REST 架构的灵魂驱动
在 RESTful 架构中,** 超媒体(Hypermedia)** 是一个核心概念,它体现了 REST 的 “表述性状态转移(Representational State Transfer)” 的本质,也是区分 “真 RESTful API” 与 “伪 RESTful AP…...