Python物理学有限差分微分求解器和动画波形传播
🎯要点
Python数值和符号计算:
- 振动常微分方程:🎯中心差分求解器,绘制移动窗口研究长时间序列。🎯符号计算离散方程量化误差。🎯Python数值对比正向欧拉方法,反向欧拉方法,克兰克-尼科尔森方法和龙格-库塔法解。🎯数值计算振动能量数值收敛。🎯欧拉-克罗默方法求解器。🎯交错网格法求解器。🎯使用线性/二次函数和符号计算验证常微分方程。🎯线性/二次阻尼求解器和验证函数,绘制阻尼正弦函数图。🎯绘制钟摆动态自由体图模拟,创建求解器计算。🎯模拟弹性摆。
- 波形运动偏微分方程:🎯弹簧波形模拟:方程算式转换,制定递归算法,代码实现数值求解器,结果动画演示,二次解和敛率的验证函数。示例:创建吉他弦一维波形方程数值求解器,动画模拟弦振动波形。🎯反射边界的诺依曼条件,代码实现一维波形方程,验证函数检测结果。🎯可变波速,代码实现可变系数。🎯代码实现给定条件下,通用一维波形方程求解器。🎯差分方程正弦和余弦波分析,代码实现网格,离散傅里叶变换,计算对应频率。🎯对离散化参数进行泰勒级数展开,代码计算数值色散关系,代码计算二维数值色散关系并绘制二维数值色散误差结果图。🎯代码解二维线性波形方程,矢量化计算函数代码,高斯函数绘制波形在正方形中传播。
- 扩散偏微方程:🎯代码实现具有边界条件的一维扩散求解器,代码验证求解器,动画可视化正向欧拉结果。🎯实现前向欧拉算法和稳定条件下一维求解器,实现求解器矢量化函数 🎯一维扩散方程隐性方法:代码实现反向欧拉法求解器,及其矢量化函数。🎯二维和三维扩散方程求解器。🎯异质介质中的扩散离散化后:代码实现求解器,稀疏矩阵处理。🎯分段恒定介质中扩散的代码实现,绘图可视化恒定扩散系数结果。🎯实现稠密系数矩阵求解器,数值验证。🎯代码实现稀疏稀疏矩阵计算。🎯雅可比方法代码实现,解线性系统。
- 平流方程,非线性问题
🍇Python热方程有限差分计算示例
热方程基本上是一个偏微分方程,即:
∂ u ∂ t − α ∇ u = 0 \frac{\partial u}{\partial t}-\alpha \nabla u=0 ∂t∂u−α∇u=0
如果我们想用二维(笛卡尔)求解,我们可以这样写上面的热方程
∂ u ∂ t − α ( ∂ 2 u ∂ x + ∂ 2 u ∂ y ) = 0 \frac{\partial u}{\partial t}-\alpha\left(\frac{\partial^2 u}{\partial x}+\frac{\partial^2 u}{\partial y}\right)=0 ∂t∂u−α(∂x∂2u+∂y∂2u)=0
其中 u u u是我们想要知道的数量, t t t是时间变量, x x x和 y y y是空间变量, α \alpha α是扩散常数。所以基本上我们希望在 x x x 和 y y y 中的任何地方以及随着时间的 t t t 找到解决方案 u u u。现在让我们简单地了解一下有限差分法。有限差分法是一种通过有限差分逼近导数来求解微分方程的数值方法。请记住导数的定义是:
f ′ ( a ) = lim h → 0 f ( a + h ) − f ( a ) h f^{\prime}(a)=\lim _{h \rightarrow 0} \frac{f(a+h)-f(a)}{h} f′(a)=h→0limhf(a+h)−f(a)
在有限差分法中,我们对其进行近似并去除限制。 因此,我们不使用微分和极限符号,而是使用 delta 符号,即有限差分。 请注意,这过于简单化了,因为我们必须使用泰勒级数展开,并通过假设某些项足够小来推导出它,但我们得到了该方法背后的粗略想法。
f ′ ( a ) ≈ f ( a + h ) − f ( a ) h f^{\prime}(a) \approx \frac{f(a+h)-f(a)}{h} f′(a)≈hf(a+h)−f(a)
在有限差分方法中,我们将“离散化”空间域和时间间隔 x、y 和 t。我们可以这样写
x i = i Δ x y j = j Δ y t k = k Δ t \begin{aligned} &x_i=i \Delta x\\ &y_j=j \Delta y\\ &t_k=k \Delta t \end{aligned} xi=iΔxyj=jΔytk=kΔt
正如我们所看到的, i 、 j i、j i、j 和 k k k 分别是 x 、 y x、y x、y 和 t t t 的每个差异的步骤。我们想要的是解 u u u,即
u ( x , y , t ) = u i , j k u(x, y, t)=u_{i, j}^k u(x,y,t)=ui,jk
请注意, k k k 是上标,表示 u u u 的时间步长。我们可以使用有限差分法写出上面的热方程,如下所示
u i , j k + 1 − u i , j k Δ t − α ( u i + 1 , j k − 2 u i , j k + u i − 1 , j k Δ x 2 + u i , j + 1 k − 2 u i , j k + u i , j − 1 k Δ y 2 ) = 0 \frac{u_{i, j}^{k+1}-u_{i, j}^k}{\Delta t}-\alpha\left(\frac{u_{i+1, j}^k-2 u_{i, j}^k+u_{i-1, j}^k}{\Delta x^2}+\frac{u_{i, j+1}^k-2 u_{i, j}^k+u_{i, j-1}^k}{\Delta y^2}\right)=0 Δtui,jk+1−ui,jk−α(Δx2ui+1,jk−2ui,jk+ui−1,jk+Δy2ui,j+1k−2ui,jk+ui,j−1k)=0
如果我们通过 Δ x = Δ y \Delta x=\Delta y Δx=Δy 排列上面的方程,我们得到最终的方程
u i , j k + 1 = γ ( u i + 1 , j k + u i − 1 , j k + u i , j + 1 k + u i , j − 1 k − 4 u i , j k ) + u i , j k u_{i, j}^{k+1}=\gamma\left(u_{i+1, j}^k+u_{i-1, j}^k+u_{i, j+1}^k+u_{i, j-1}^k-4 u_{i, j}^k\right)+u_{i, j}^k ui,jk+1=γ(ui+1,jk+ui−1,jk+ui,j+1k+ui,j−1k−4ui,jk)+ui,jk
其中, γ = α Δ t Δ x 2 \gamma=\alpha \frac{\Delta t}{\Delta x^2} γ=αΔx2Δt
对于我们的模型,我们取 Δ x = 1 \Delta x=1 Δx=1 和 α = 2.0 \alpha=2.0 α=2.0。现在我们可以使用 Python 代码以数值方式解决这个问题,以查看各处的温度(用 i i i 和 j j j 表示)和随时间变化的温度(用 k k k 表示)。我们首先导入所有必要的库,然后设置边界和初始条件。
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from matplotlib.animation import FuncAnimationplate_length = 50
max_iter_time = 1000alpha = 2.0
delta_x = 1delta_t = (delta_x ** 2)/(4 * alpha)
gamma = (alpha * delta_t) / (delta_x ** 2)u = np.empty((max_iter_time, plate_length, plate_length))u_initial = 0.0u_top = 100.0
u_left = 0.0
u_bottom = 0.0
u_right = 0.0u.fill(u_initial)u[:, (plate_length-1):, :] = u_top
u[:, :, :1] = u_left
u[:, :1, 1:] = u_bottom
u[:, :, (plate_length-1):] = u_right我们已经设置了初始条件和边界条件,让我们根据上面推导的有限差分方法编写计算函数。
def calculate(u):for k in range(0, max_iter_time-1, 1):for i in range(1, plate_length-1, delta_x):for j in range(1, plate_length-1, delta_x):u[k + 1, i, j] = gamma * (u[k][i+1][j] + u[k][i-1][j] + u[k][i][j+1] + u[k][i][j-1] - 4*u[k][i][j]) + u[k][i][j]return u
让我们准备绘图函数,以便我们可以将解(对于每个 k)可视化为热图。我们使用Matplotlib库,它很容易使用。
参阅一:计算思维
参阅二:亚图跨际
相关文章:

Python物理学有限差分微分求解器和动画波形传播
🎯要点 Python数值和符号计算: 振动常微分方程:🎯中心差分求解器,绘制移动窗口研究长时间序列。🎯符号计算离散方程量化误差。🎯Python数值对比正向欧拉方法,反向欧拉方法…...
游戏本续航@控制中心的省电模式效果如何
文章目录 节能模式长续航模式👺相关工具 节能模式长续航模式👺 蓝天模具Control Center中的模式 根据我的试验,以及软件的提示,可以发现 Power Saving是最省电的,儿Quiet模式并不省电,它会启用独立显卡,只不过风扇的转速不像娱乐模式和性能模式那么积极而…...

centOS 安装MySQL8.0
1.配置yum仓库 rpm --import https://repo.mysql.com/RPM-GPG-KEY-mysql-2022 2.安装MySQL8.x版本 yum库 rpm -Uvh https://dev.mysql.com/get/mysql80-community-release-el7-2.noarch.rpm 或者 wget https://dev.mysql.com/get/mysql80-community-release-el7-2.noarch…...

力扣 1.两数之和
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。 你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。 你可以按任意顺序返回…...

Occupancy field----其他应用
文章目录 3D表示技术的概述:Signed Distance Function (SDF)Occupancy Field (占用场)神经辐射场(NeRF) Occupancy Networks 是一种基于Occupancy表示的可微分模型,它在与其他3D表示技术(例如点云、体素和三角面片&…...

Spring_MVC
web.xml配置文件 <?xml version"1.0" encoding"UTF-8"?> <web-app xmlns"http://xmlns.jcp.org/xml/ns/javaee"xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://xmlns.jcp.org/xml…...

【动手学深度学习】深入浅出深度学习之线性神经网络
目录 🌞一、实验目的 🌞二、实验准备 🌞三、实验内容 🌼1. 线性回归 🌻1.1 矢量化加速 🌻1.2 正态分布与平方损失 🌼2. 线性回归的从零开始实现 🌻2.1. 生成数据集 &#x…...
2024/3/26 C++作业
定义一个矩形类(Rectangle),包含私有成员:长(length)、宽(width), 定义成员函数: 设置长度:void set_l(int l) 设置宽度:void set_w(int w) 获取长度:int…...

LinkedList讲解指南
咦咦咦,各位小可爱,我是你们的好伙伴——bug菌,今天又来给大家普及Java SE相关知识点了,别躲起来啊,听我讲干货还不快点赞,赞多了我就有动力讲得更嗨啦!所以呀,养成先点赞后阅读的好…...

IP如何异地共享文件?
【天联】 组网由于操作简单、跨平台应用、无网络要求、独创的安全加速方案等原因,被几十万用户广泛应用,解决了各行业客户的远程连接需求。采用穿透技术,简单易用,不需要在硬件设备中端口映射即可实现远程访问。 异地共享文件 在…...

HCIA-Datacom H12-811 题库补充(3/28)
完整题库及答案解析,请直接扫描上方二维码,持续更新中 OSPFv3使用哪个区域号标识骨干区域? A:0 B:3 C:1 D:2 答案:A 解析:AREA 号0就是骨干区域。 STP下游设备通知上游…...

轻量级富文本编辑 Trumbowyg —— 基于 jQuery 插件配置
使用方法👇 首先,添加jQuery到页面<body>位置: <script src"http://libs.baidu.com/jquery/1.8.3/jquery.min.js"></script> <script>window.jQuery || document.write(<script src"js/vendor/jquery-1.10.2.min.js&qu…...
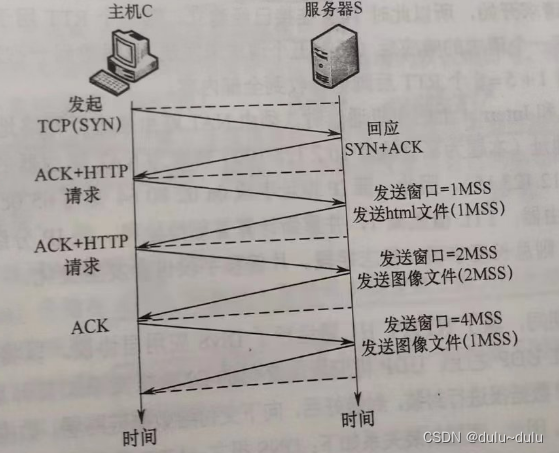
那些王道书里的题目-----计算机网络篇
注:仅记录个人认为有启发的题目 p155 34.下列四个地址块中,与地址块 172.16.166.192/26 不重叠,且与172.16.166.192/26聚合后的地址块不会引入多余地址的是() A.172.16.166.192/27 B.172.16.166.128/26 …...

【前端学习——js篇】 10.this指向
具体见:https://github.com/febobo/web-interview 10.this指向 根据不同的使用场合,this有不同的值,主要分为下面几种情况: 默认绑定隐式绑定new绑定显示绑定 ①默认绑定 全局环境中定义person函数,内部使用this关…...

项目搭建之统一返回值
自定义枚举类 Getter public enum ReturnCodeEnum {/*** 操作失败**/RC999("999","操作XXX失败"),/*** 操作成功**/RC200("200","success"),/*** 服务降级**/RC201("201","服务开启降级保护,请稍后再试!"),/*** …...

嵌入式和 Java 走哪条路?
最近看到一个物联网大三学生的疑问,原话如下: 本人普通本科物联网工程专业,开学大三,现在就很迷茫,不打算考研了,准备直接就业,平时一直在实验室参加飞思卡尔智能车比赛,本来是想走嵌…...

C++ 控制语句(一)
一 顺序结构 程序的基本结构有三种: 顺序结构、分支结构、循环结构 大量的实际问题需要通过各种控制流程来解决。 1.1 顺序结构 1.2 简单语句和复合语句 二 循环 2.1 for循环 语句流程图 注意:使用for语句的灵活性 三 while语句 四 do while语句...

mysql 用户管理-权限表
学习了《mysql5.7安装》,就先再了解下用户管理,先了解下权限表。 MySQL是一个多用户数据库,具有功能强大的访问控制系统,可以为不同用户指定允许 的权限。MySQL用户可以分为普通用户和root用户。root 用户是超级管理员,拥有所有权…...
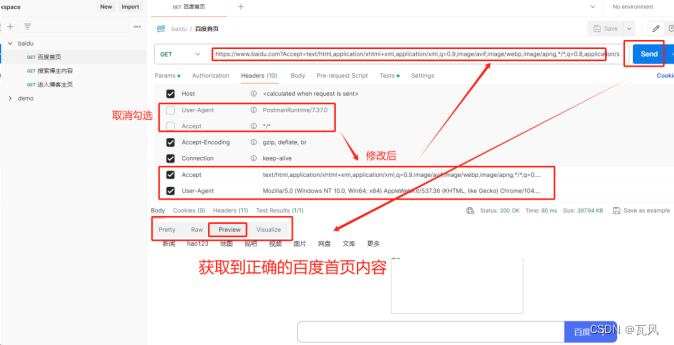
【Postman如何进行接口测试简单详细操作实例】
1、下载Postman postman下载地址:Download Postman | Get Started for Free 2、安装Postman (1)双击下载好的postman-setup.exe文件,进行安装postman工具 (2)安装完成后,在桌面找到并打开postman软件,输入邮箱和密码进行登录&a…...

docker搭建Project Calico环境
Project Calico 是一个开源的网络和网络安全解决方案,专为容器、虚拟机和本地工作负载设计。它提供了高度可扩展的网络层,支持广泛的容器编排平台,如 Kubernetes、Docker Swarm和OpenStack。Calico 的主要特点包括: 支持多层网络策略,包括基于角色的访问控制(RBAC)。提供网…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...
)
LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别(二)
在上一篇文章中,我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调,以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后,如何调用这个模型进行人脸情感识别的具体代码实现,包括详细的步骤和注释。 模型调用步骤 环境准备:确保安装了必要的Python库。…...

何谓AI编程【02】AI编程官网以优雅草星云智控为例建设实践-完善顶部-建立各项子页-调整排版-优雅草卓伊凡
何谓AI编程【02】AI编程官网以优雅草星云智控为例建设实践-完善顶部-建立各项子页-调整排版-优雅草卓伊凡 背景 我们以建设星云智控官网来做AI编程实践,很多人以为AI已经强大到不需要程序员了,其实不是,AI更加需要程序员,普通人…...

UE5 音效系统
一.音效管理 音乐一般都是WAV,创建一个背景音乐类SoudClass,一个音效类SoundClass。所有的音乐都分为这两个类。再创建一个总音乐类,将上述两个作为它的子类。 接着我们创建一个音乐混合类SoundMix,将上述三个类翻入其中,通过它管理每个音乐…...
