【动手学深度学习】深入浅出深度学习之线性神经网络



目录
🌞一、实验目的
🌞二、实验准备
🌞三、实验内容
🌼1. 线性回归
🌻1.1 矢量化加速
🌻1.2 正态分布与平方损失
🌼2. 线性回归的从零开始实现
🌻2.1. 生成数据集
🌻2.2 读取数据集
🌻2.3. 初始化模型参数
🌻2.4. 定义模型
🌻2.5. 定义损失函数
🌻2.6. 定义优化算法
🌻2.7. 训练
🌻2.8 小结
🌻2.9 练习
🌼3. 线性回归的简洁实现
🌻3.1. 生成数据集
🌻3.2. 读取数据集
🌻3.3 定义模型
🌻3.4 初始化模型参数
🌻3.5 定义损失函数
🌻3.6 定义优化算法
🌻3.7 训练
🌻3.8 小结
🌻3.9 练习
🌞四、实验心得
🌞一、实验目的
- 熟悉PyTorch框架:了解PyTorch的基本概念、数据结构和核心函数;
- 创建线性回归模型:使用PyTorch构建一个简单的线性回归模型,该模型能够学习输入特征和目标变量之间的线性关系;
- 线性回归从零开始实现及其简洁实现,并完成章节后习题。
🌞二、实验准备
- 根据GPU安装pytorch版本实现GPU运行实验代码;
- 配置环境用来运行 Python、Jupyter Notebook和相关库等相关库。
🌞三、实验内容
资源获取:关注公众号【科创视野】回复 深度学习
🌼1. 线性回归
(1)使用jupyter notebook新增的pytorch环境新建ipynb文件,完成线性回归从零开始实现的实验代码与练习结果如下:
🌻1.1 矢量化加速
%matplotlib inline
import math
import time
import numpy as np
import torch
from d2l import torch as d2ln = 10000
a = torch.ones([n])
b = torch.ones([n])class Timer: #@save"""记录多次运行时间"""def __init__(self):self.times = []self.start()def start(self):"""启动计时器"""self.tik = time.time()def stop(self):"""停止计时器并将时间记录在列表中"""self.times.append(time.time() - self.tik)return self.times[-1]def avg(self):"""返回平均时间"""return sum(self.times) / len(self.times)def sum(self):"""返回时间总和"""return sum(self.times)def cumsum(self):"""返回累计时间"""return np.array(self.times).cumsum().tolist()c = torch.zeros(n)
timer = Timer()
for i in range(n):c[i] = a[i] + b[i]
f'{timer.stop():.5f} sec'输出结果

🌻1.2 正态分布与平方损失
def normal(x, mu, sigma):p = 1 / math.sqrt(2 * math.pi * sigma**2)return p * np.exp(-0.5 / sigma**2 * (x - mu)**2)# 再次使用numpy进行可视化
x = np.arange(-7, 7, 0.01)# 均值和标准差对
params = [(0, 1), (0, 2), (3, 1)]
d2l.plot(x, [normal(x, mu, sigma) for mu, sigma in params], xlabel='x',ylabel='p(x)', figsize=(4.5, 2.5),legend=[f'mean {mu}, std {sigma}' for mu, sigma in params])输出结果

🌼2. 线性回归的从零开始实现
%matplotlib inline
import random
import torch
from d2l import torch as d2l🌻2.1. 生成数据集
def synthetic_data(w, b, num_examples): #@save"""生成y=Xw+b+噪声"""X = torch.normal(0, 1, (num_examples, len(w)))y = torch.matmul(X, w) + by += torch.normal(0, 0.01, y.shape)return X, y.reshape((-1, 1))true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)print('features:', features[0],'\nlabel:', labels[0])输出结果

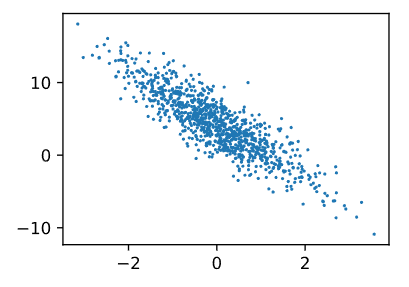
d2l.set_figsize()
d2l.plt.scatter(features[:, 1].detach().numpy(), labels.detach().numpy(), 1);输出结果
🌻2.2 读取数据集
def data_iter(batch_size, features, labels):num_examples = len(features)indices = list(range(num_examples))# 这些样本是随机读取的,没有特定的顺序random.shuffle(indices)for i in range(0, num_examples, batch_size):batch_indices = torch.tensor(indices[i: min(i + batch_size, num_examples)])yield features[batch_indices], labels[batch_indices]batch_size = 10for X, y in data_iter(batch_size, features, labels):print(X, '\n', y)break输出结果

🌻2.3. 初始化模型参数
w = torch.normal(0, 0.01, size=(2,1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
w,b输出结果

🌻2.4. 定义模型
def linreg(X, w, b): #@save"""线性回归模型"""return torch.matmul(X, w) + b🌻2.5. 定义损失函数
def squared_loss(y_hat, y): #@save"""均方损失"""return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2🌻2.6. 定义优化算法
def sgd(params, lr, batch_size): #@save"""小批量随机梯度下降"""with torch.no_grad():for param in params:param -= lr * param.grad / batch_sizeparam.grad.zero_()🌻2.7. 训练
lr = 0.03
num_epochs = 3
net = linreg
loss = squared_lossfor epoch in range(num_epochs):for X, y in data_iter(batch_size, features, labels):l = loss(net(X, w, b), y) # X和y的小批量损失# 因为l形状是(batch_size,1),而不是一个标量。l中的所有元素被加到一起,# 并以此计算关于[w,b]的梯度l.sum().backward()sgd([w, b], lr, batch_size) # 使用参数的梯度更新参数with torch.no_grad():train_l = loss(net(features, w, b), labels)print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')输出结果

print(f'w的估计误差: {true_w - w.reshape(true_w.shape)}')
print(f'b的估计误差: {true_b - b}')输出结果

🌻2.8 小结
我们学习了深度网络是如何实现和优化的。在这一过程中只使用张量和自动微分,不需要定义层或复杂的优化器。这一节只触及到了表面知识。在下面的部分中,我们将基于刚刚介绍的概念描述其他模型,并学习如何更简洁地实现其他模型。
🌻2.9 练习
1.如果我们将权重初始化为零,会发生什么。算法仍然有效吗?
# 在单层网络中(一层线性回归层),将权重初始化为零时可以的,但是网络层数加深后,在全连接的情况下,
# 在反向传播的时候,由于权重的对称性会导致出现隐藏神经元的对称性,使得多个隐藏神经元的作用就如同
# 1个神经元,算法还是有效的,但是效果不大好。参考:https://zhuanlan.zhihu.com/p/75879624。2.假设试图为电压和电流的关系建立一个模型。自动微分可以用来学习模型的参数吗?
# 可以的,建立模型U=IW+b,然后采集(U,I)的数据集,通过自动微分即可学习W和b的参数。
import torch
import random
from d2l import torch as d2l
#生成数据集
def synthetic_data(r, b, num_examples):I = torch.normal(0, 1, (num_examples, len(r)))u = torch.matmul(I, r) + bu += torch.normal(0, 0.01, u.shape) # 噪声return I, u.reshape((-1, 1)) # 标量转换为向量true_r = torch.tensor([20.0])
true_b = 0.01
features, labels = synthetic_data(true_r, true_b, 1000)#读取数据集
def data_iter(batch_size, features, labels):num_examples = len(features)indices = list(range(num_examples))random.shuffle(indices)for i in range(0, num_examples, batch_size):batch_indices = torch.tensor(indices[i: min(i + batch_size, num_examples)])yield features[batch_indices],labels[batch_indices]batch_size = 10
# 初始化权重
r = torch.normal(0,0.01,size = ((1,1)), requires_grad = True)
b = torch.zeros(1, requires_grad = True)# 定义模型
def linreg(I, r, b):return torch.matmul(I, r) + b
# 损失函数
def square_loss(u_hat, u):return (u_hat - u.reshape(u_hat.shape)) ** 2/2
# 优化算法
def sgd(params, lr, batch_size):with torch.no_grad():for param in params:param -= lr * param.grad/batch_sizeparam.grad.zero_()lr = 0.03
num_epochs = 10
net = linreg
loss = square_lossfor epoch in range(num_epochs):for I, u in data_iter(batch_size, features, labels):l = loss(net(I, r, b), u)l.sum().backward()sgd([r, b], lr, batch_size)with torch.no_grad():train_l = loss(net(features, r, b), labels)print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')
print(r)
print(b)
print(f'r的估计误差: {true_r - r.reshape(true_r.shape)}')
print(f'b的估计误差: {true_b - b}')
输出结果

3.能基于普朗克定律使用光谱能量密度来确定物体的温度吗?
# 3
# 普朗克公式
# x:波长
# T:温度
import torch
import random
from d2l import torch as d2l#生成数据集
def synthetic_data(x, num_examples):T = torch.normal(0, 1, (num_examples, len(x)))u = c1 / ((x ** 5) * ((torch.exp(c2 / (x * T))) - 1));u += torch.normal(0, 0.01, u.shape) # 噪声return T, u.reshape((-1, 1)) # 标量转换为向量c1 = 3.7414*10**8 # c1常量
c2 = 1.43879*10**4 # c2常量
true_x = torch.tensor([500.0])features, labels = synthetic_data(true_x, 1000)#读取数据集
def data_iter(batch_size, features, labels):num_examples = len(features)indices = list(range(num_examples))random.shuffle(indices)for i in range(0, num_examples, batch_size):batch_indices = torch.tensor(indices[i: min(i + batch_size, num_examples)])yield features[batch_indices],labels[batch_indices]batch_size = 10
# 初始化权重
x = torch.normal(0,0.01,size = ((1,1)), requires_grad = True)# 定义模型
def planck_formula(T, x):return c1 / ((x ** 5) * ((torch.exp(c2 / (x * T))) - 1))
# 损失函数
def square_loss(u_hat, u):return (u_hat - u.reshape(u_hat.shape)) ** 2/2
# 优化算法
def sgd(params, lr, batch_size):with torch.no_grad():for param in params:param -= lr * param.grad/batch_sizeparam.grad.zero_()lr = 0.001
num_epochs = 10
net = planck_formula
loss = square_lossfor epoch in range(num_epochs):for T, u in data_iter(batch_size, features, labels):l = loss(net(T, x), u)l.sum().backward()sgd([x], lr, batch_size)with torch.no_grad():train_l = loss(net(features, x), labels)print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')print(f'r的估计误差: {true_x - x.reshape(true_x.shape)}')
输出结果

4.计算二阶导数时可能会遇到什么问题?这些问题可以如何解决?
# 一阶导数的正向计算图无法直接获得,可以通过保存一阶导数的计算图使得可以求二阶导数(create_graph和retain_graph都置为True,
# 保存原函数和一阶导数的正向计算图)。实验如下:
import torchx = torch.randn((2), requires_grad=True)
y = x**3dy = torch.autograd.grad(y, x, grad_outputs=torch.ones(x.shape),retain_graph=True, create_graph=True)
dy2 = torch.autograd.grad(dy, x, grad_outputs=torch.ones(x.shape))dy_ = 3*x**2
dy2_ = 6*xprint("======================================================")
print(dy, dy_)
print("======================================================")
print(dy2, dy2_)
输出结果

5.为什么在squared_loss函数中需要使用reshape函数?
# 以防y^和y,一个是行向量、一个是列向量,使用reshape,可以确保shape一样。6.尝试使用不同的学习率,观察损失函数值下降的快慢。
# ①学习率过大前期下降很快,但是后面不容易收敛;
# ②学习率过小损失函数下降会很慢。7.如果样本个数不能被批量大小整除,data_iter函数的行为会有什么变化?
# 报错。🌼3. 线性回归的简洁实现
(1)使用jupyter notebook新增的pytorch环境新建ipynb文件,完成线性回归的简洁实现的实验代码与练习结果如下:
🌻3.1. 生成数据集
import numpy as np
import torch
from torch.utils import data
from d2l import torch as d2ltrue_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = d2l.synthetic_data(true_w, true_b, 1000)🌻3.2. 读取数据集
def load_array(data_arrays, batch_size, is_train=True): #@save"""构造一个PyTorch数据迭代器"""dataset = data.TensorDataset(*data_arrays)return data.DataLoader(dataset, batch_size, shuffle=is_train)batch_size = 10
data_iter = load_array((features, labels), batch_size)next(iter(data_iter))输出结果

🌻3.3 定义模型
# nn是神经网络的缩写
from torch import nnnet = nn.Sequential(nn.Linear(2, 1))🌻3.4 初始化模型参数
net[0].weight.data.normal_(0, 0.01)
net[0].bias.data.fill_(0)输出结果
![]()
🌻3.5 定义损失函数
loss = nn.MSELoss()🌻3.6 定义优化算法
trainer = torch.optim.SGD(net.parameters(), lr=0.03)🌻3.7 训练
num_epochs = 3
for epoch in range(num_epochs):for X, y in data_iter:l = loss(net(X) ,y)trainer.zero_grad()l.backward()trainer.step()l = loss(net(features), labels)print(f'epoch {epoch + 1}, loss {l:f}')输出结果

w = net[0].weight.data
print('w的估计误差:', true_w - w.reshape(true_w.shape))
b = net[0].bias.data
print('b的估计误差:', true_b - b)输出结果
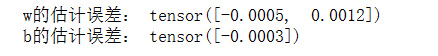
🌻3.8 小结
- 我们可以使用PyTorch的高级API更简洁地实现模型。
- 在PyTorch中,data模块提供了数据处理工具,nn模块定义了大量的神经网络层和常见损失函数。
- 我们可以通过_结尾的方法将参数替换,从而初始化参数。
🌻3.9 练习
1.如果将小批量的总损失替换为小批量损失的平均值,需要如何更改学习率?
# 将学习率除以batchsize。2.查看深度学习框架文档,它们提供了哪些损失函数和初始化方法?
用Huber损失代替原损失,即
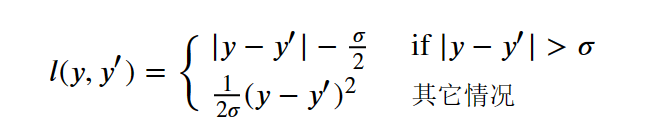
# Huber损失可以用torch自带的函数解决
torch.nn.SmoothL1Loss()
# 也可以自己写
import torch.nn as nn
import torch.nn.functional as Fclass HuberLoss(nn.Module):def __init__(self, sigma):super(HuberLoss, self).__init__()self.sigma = sigmadef forward(self, y, y_hat):if F.l1_loss(y, y_hat) > self.sigma:loss = F.l1_loss(y, y_hat) - self.sigma/2else:loss = (1/(2*self.sigma))*F.mse_loss(y, y_hat)return loss#%%
import numpy as np
import torch
from torch.utils import data
from d2l import torch as d2l#%%
true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = d2l.synthetic_data(true_w, true_b, 1000)def load_array(data_arrays, batch_size, is_train = True): #@save'''pytorch数据迭代器'''dataset = data.TensorDataset(*data_arrays) # 把输入的两类数据一一对应;*表示对list解开入参return data.DataLoader(dataset, batch_size, shuffle = is_train) # 重新排序batch_size = 10
data_iter = load_array((features, labels), batch_size) # 和手动实现中data_iter使用方法相同#%%
# 构造迭代器并验证data_iter的效果
next(iter(data_iter)) # 获得第一个batch的数据#%% 定义模型
from torch import nn
net = nn.Sequential(nn.Linear(2, 1)) # Linear中两个参数一个表示输入形状一个表示输出形状
# sequential相当于一个存放各层数据的list,单层时也可以只用Linear#%% 初始化模型参数
# 使用net[0]选择神经网络中的第一层
net[0].weight.data.normal_(0, 0.01) # 正态分布
net[0].bias.data.fill_(0)#%% 定义损失函数
loss = torch.nn.HuberLoss()
#%% 定义优化算法
trainer = torch.optim.SGD(net.parameters(), lr=0.03) # optim module中的SGD
#%% 训练
num_epochs = 3
for epoch in range(num_epochs):for X, y in data_iter:l = loss(net(X), y)trainer.zero_grad()l.backward()trainer.step()l = loss(net(features), labels)print(f'epoch {epoch+1}, loss {l:f}')#%% 查看误差
w = net[0].weight.data
print('w的估计误差:', true_w - w.reshape(true_w.shape))
b = net[0].bias.data
print('b的估计误差:', true_b - b)
输出结果

3.如何访问线性回归的梯度?
#假如是多层网络,可以用一个self.xxx=某层,然后在外面通过net.xxx.weight.grad和net.xxx.bias.grad把梯度给拿出来。
net[0].weight.grad
net[0].bias.grad
输出结果
![]()
🌞四、实验心得
通过此次实验,我熟悉了PyTorch框架以及PyTorch的基本概念、数据结构和核心函数;创建了线性回归模型,使用PyTorch构建一个简单的线性回归模型;完成了线性回归从零开始实现及其简洁实现以及章节后习题。明白了以下几点:
1.深度学习的关键要素包括训练数据、损失函数、优化算法以及模型本身。这些要素相互作用,共同决定了模型的性能和表现。
2.矢量化是一种重要的数学表达方式,它能使数学计算更加简洁高效。通过使用向量和矩阵运算,可以将复杂的计算过程转化为简单的线性代数运算,从而提高计算效率。
3.最小化目标函数和执行极大似然估计是等价的。在机器学习中,通常通过最小化损失函数来优化模型。而在概率统计中,可以通过最大化似然函数来估计模型参数。这两种方法在数学上是等价的,都可以用于优化模型。
4.线性回归模型可以被看作是一个简单的神经网络模型。它只包含一个输入层和一个输出层,其中输入层的神经元数量与输入特征的维度相同,输出层的神经元数量为1。线性回归模型可以用于解决回归问题,通过学习输入特征与输出之间的线性关系来进行预测。
5.在深度学习中,学习了如何实现和优化深度神经网络。在这个过程中,只使用张量(Tensor)和自动微分(Automatic Differentiation),而不需要手动定义神经网络层或复杂的优化器。张量是深度学习中的基本数据结构,它可以表示多维数组,并支持各种数学运算。自动微分是一种计算梯度的技术,它能够自动计算函数相对于输入的导数,从而实现了反向传播算法。
6.为了更加简洁地实现模型,可以利用PyTorch的高级API。在PyTorch中,data模块提供了数据处理工具,包括数据加载、预处理和批处理等功能,使得数据的处理变得更加方便和高效。nn模块则提供了大量的神经网络层和常见损失函数的定义,可以直接使用这些层和函数来构建和训练模型,无需手动实现。此外还可以通过使用_结尾的方法来进行参数的替换和初始化,从而更加灵活地管理模型的参数。


相关文章:

【动手学深度学习】深入浅出深度学习之线性神经网络
目录 🌞一、实验目的 🌞二、实验准备 🌞三、实验内容 🌼1. 线性回归 🌻1.1 矢量化加速 🌻1.2 正态分布与平方损失 🌼2. 线性回归的从零开始实现 🌻2.1. 生成数据集 &#x…...
2024/3/26 C++作业
定义一个矩形类(Rectangle),包含私有成员:长(length)、宽(width), 定义成员函数: 设置长度:void set_l(int l) 设置宽度:void set_w(int w) 获取长度:int…...

LinkedList讲解指南
咦咦咦,各位小可爱,我是你们的好伙伴——bug菌,今天又来给大家普及Java SE相关知识点了,别躲起来啊,听我讲干货还不快点赞,赞多了我就有动力讲得更嗨啦!所以呀,养成先点赞后阅读的好…...

IP如何异地共享文件?
【天联】 组网由于操作简单、跨平台应用、无网络要求、独创的安全加速方案等原因,被几十万用户广泛应用,解决了各行业客户的远程连接需求。采用穿透技术,简单易用,不需要在硬件设备中端口映射即可实现远程访问。 异地共享文件 在…...

HCIA-Datacom H12-811 题库补充(3/28)
完整题库及答案解析,请直接扫描上方二维码,持续更新中 OSPFv3使用哪个区域号标识骨干区域? A:0 B:3 C:1 D:2 答案:A 解析:AREA 号0就是骨干区域。 STP下游设备通知上游…...

轻量级富文本编辑 Trumbowyg —— 基于 jQuery 插件配置
使用方法👇 首先,添加jQuery到页面<body>位置: <script src"http://libs.baidu.com/jquery/1.8.3/jquery.min.js"></script> <script>window.jQuery || document.write(<script src"js/vendor/jquery-1.10.2.min.js&qu…...
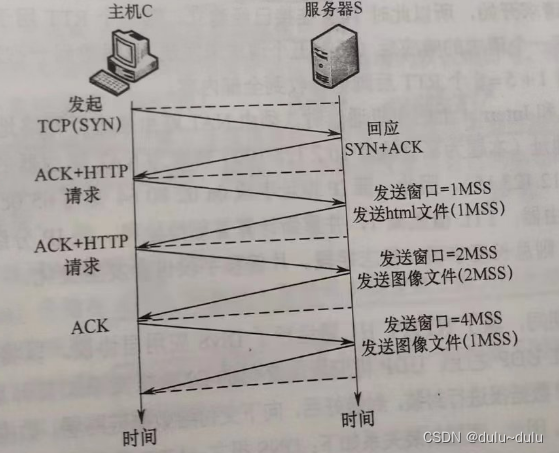
那些王道书里的题目-----计算机网络篇
注:仅记录个人认为有启发的题目 p155 34.下列四个地址块中,与地址块 172.16.166.192/26 不重叠,且与172.16.166.192/26聚合后的地址块不会引入多余地址的是() A.172.16.166.192/27 B.172.16.166.128/26 …...

【前端学习——js篇】 10.this指向
具体见:https://github.com/febobo/web-interview 10.this指向 根据不同的使用场合,this有不同的值,主要分为下面几种情况: 默认绑定隐式绑定new绑定显示绑定 ①默认绑定 全局环境中定义person函数,内部使用this关…...

项目搭建之统一返回值
自定义枚举类 Getter public enum ReturnCodeEnum {/*** 操作失败**/RC999("999","操作XXX失败"),/*** 操作成功**/RC200("200","success"),/*** 服务降级**/RC201("201","服务开启降级保护,请稍后再试!"),/*** …...

嵌入式和 Java 走哪条路?
最近看到一个物联网大三学生的疑问,原话如下: 本人普通本科物联网工程专业,开学大三,现在就很迷茫,不打算考研了,准备直接就业,平时一直在实验室参加飞思卡尔智能车比赛,本来是想走嵌…...

C++ 控制语句(一)
一 顺序结构 程序的基本结构有三种: 顺序结构、分支结构、循环结构 大量的实际问题需要通过各种控制流程来解决。 1.1 顺序结构 1.2 简单语句和复合语句 二 循环 2.1 for循环 语句流程图 注意:使用for语句的灵活性 三 while语句 四 do while语句...

mysql 用户管理-权限表
学习了《mysql5.7安装》,就先再了解下用户管理,先了解下权限表。 MySQL是一个多用户数据库,具有功能强大的访问控制系统,可以为不同用户指定允许 的权限。MySQL用户可以分为普通用户和root用户。root 用户是超级管理员,拥有所有权…...
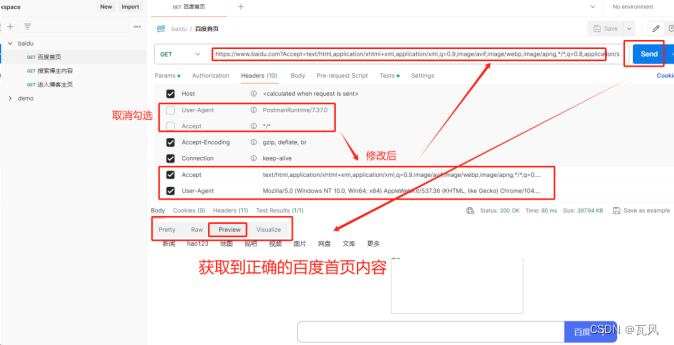
【Postman如何进行接口测试简单详细操作实例】
1、下载Postman postman下载地址:Download Postman | Get Started for Free 2、安装Postman (1)双击下载好的postman-setup.exe文件,进行安装postman工具 (2)安装完成后,在桌面找到并打开postman软件,输入邮箱和密码进行登录&a…...

docker搭建Project Calico环境
Project Calico 是一个开源的网络和网络安全解决方案,专为容器、虚拟机和本地工作负载设计。它提供了高度可扩展的网络层,支持广泛的容器编排平台,如 Kubernetes、Docker Swarm和OpenStack。Calico 的主要特点包括: 支持多层网络策略,包括基于角色的访问控制(RBAC)。提供网…...

pyecharts操作一
pyecharts 是一个用于生成Echarts图表的Python库。Echarts是百度开源的一个数据可视化JS库,可以生成一些非常酷炫的图表。 环境安装 pip install pyecharts 检查版本 import pyecharts print(pyecharts.version) 2.0.3 柱状图绘制 from pyecharts.charts impor…...

『Apisix进阶篇』动态负载均衡:APISIX的实战演练与策略应用
🚀『Apisix系列文章』探索新一代微服务体系下的API管理新范式与最佳实践 【点击此跳转】 📣读完这篇文章里你能收获到 🎯 掌握APISIX中多种负载均衡策略的原理及其适用场景。📈 学习如何通过APISIX的Admin API和Dashboard进行负…...

【开发篇】十一、GC调优的分析工具
文章目录 1、调优的主要指标2、工具一:jstat3、工具二:Visual VM的插件4、工具三:Prometheus Grafana5、生成GC日志6、工具四:GC Viewer7、工具五:GCeasy GC调优,是为了避免因垃圾回收引起程序性能下降&am…...
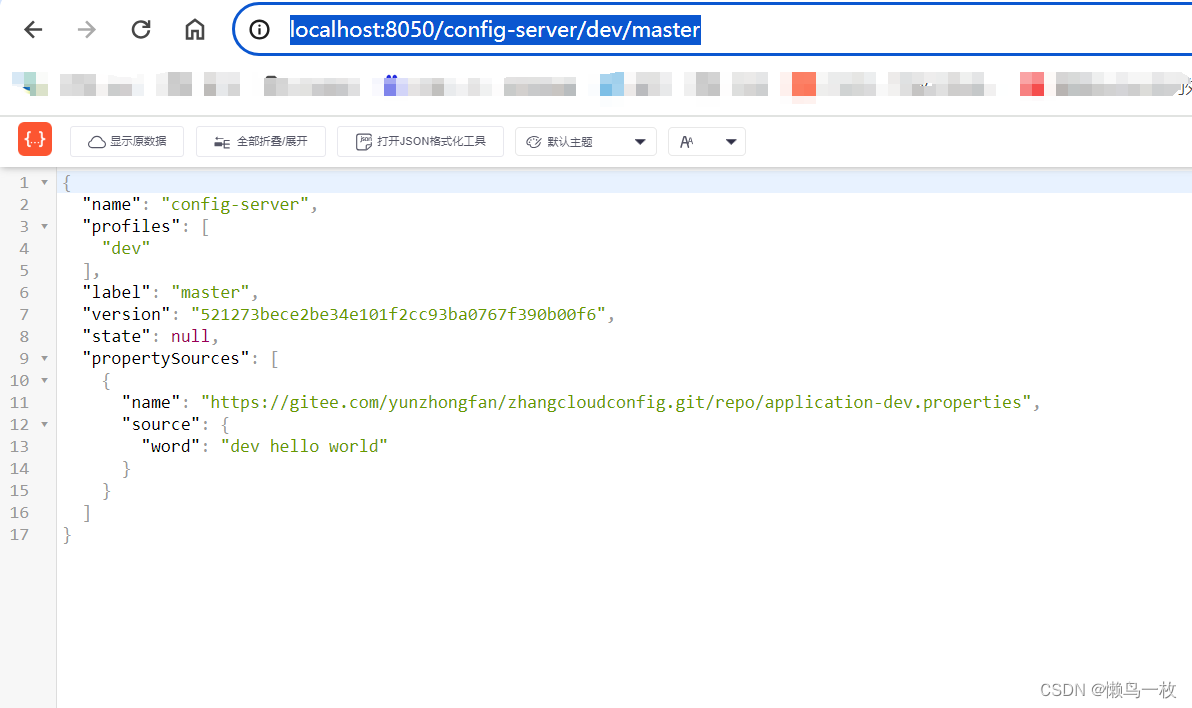
SpringCloudConfig 使用git搭建配置中心
一 SpringCloudConfig 配置搭建步骤 1.引入 依赖pom文件 引入 spring-cloud-config-server 是因为已经配置了注册中心 <dependencies><dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-config-server</…...

c#基础-引用类型和值类型的区别
在C#中,数据类型分为两类:值类型和引用类型。 值类型:直接存储数据,分配在栈(Stack)上。常见的值类型包括基本数据类型(int, float, double等),结构体(struct),枚举(enum)等。 引用类型:存储数据的引用和对象,分配在托管堆(Heap)上。常见的引用类型包括类(cla…...

面试题-3.20
1、__FILE__表示什么意思? __FILE__:当前文件的完整路径和文件名 __LINE__:当前行 __DIR__:当前文件所在的目录 2、如何获取客户端的IP地址? 通过超全局数组$_SERVER:echo $_SERVER[REMOTE_PORT]; 3、写…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...
