吴恩达深度学习笔记:神经网络的编程基础2.5-2.8
目录
- 第一门课:神经网络和深度学习 (Neural Networks and Deep Learning)
- 第二周:神经网络的编程基础 (Basics of Neural Network programming)
- 2.5 导数(Derivatives)
- 2.6 更多的导数例子(More Derivative Examples)
- 2.7 计算图(Computation Graph)
- 2.8 使用计算图求导数(Derivatives with a Computation Graph)
第一门课:神经网络和深度学习 (Neural Networks and Deep Learning)
第二周:神经网络的编程基础 (Basics of Neural Network programming)
2.5 导数(Derivatives)
这个视频我主要是想帮你获得对微积分和导数直观的理解。或许你认为自从大学毕以后你再也没有接触微积分。这取决于你什么时候毕业,也许有一段时间了,如果你顾虑这点,请不要担心。为了高效应用神经网络和深度学习,你并不需要非常深入理解微积分。因此如果你观看这个视频或者以后的视频时心想:“哇哦,这些知识、这些运算对我来说很复杂。”我给你的建议是:坚持学习视频,最好下课后做作业,成功的完成编程作业,然后你就可以使用深度学习了。在第四周之后的学习中,你会看到定义的很多种类的函数,通过微积分他们能够帮助你把所有的知识结合起来,其中有的叫做前向函数和反向函数,因此你不需要了解所有你使用的那些微积分中的函数。所以你不用担心他们,除此之外在对深度学习的尝试中,这周我们要进一步深入了解微积分的细节。所有你只需要直观地认识微积分,用来构建和成功的应用这些算法。最后,如果你是精通微积分的那一小部分人群,你对微积分非常熟悉,你可以跳过这部分视频。其他同学让我们开始深入学习导数。

一个函数𝑓(𝑎) = 3𝑎,它是一条直线。下面我们来简单理解下导数。让我们看看函数中几个点,假定𝑎 = 2,那么𝑓(𝑎)是𝑎的 3 倍等于 6,也就是说如果𝑎 = 2,那么函数𝑓(𝑎) = 6。假定稍微改变一点点𝑎的值,只增加一点,变为 2.001,这时𝑎将向右做微小的移动。0.001 的差别实在是太小了,不能在图中显示出来,我们把它右移一点,现在𝑓(𝑎)等于𝑎的 3 倍是 6.003,画在图里,比例不太符合。请看绿色高亮部分的这个小三角形,如果向右移动 0.001,那么𝑓(𝑎)增加 0.003,𝑓(𝑎)的值增加 3 倍于右移的𝑎,因此我们说函数𝑓(𝑎)在𝑎 = 2,.是这个导数的斜率,或者说,当𝑎 = 2时,斜率是 3。导数这个概念意味着斜率,导数听起来是一个很可怕、很令人惊恐的词,但是斜率以一种很友好的方式来描述导数这个概念。所以提到导数,我们把它当作函数的斜率就好了。更正式的斜率定义为在上图这个绿色的小三角形中,高除以宽。即斜率等于 0.003 除以 0.001,等于 3。或者说导数等于 3,这表示当你将𝑎右移 0.001,𝑓(𝑎)的值增加 3 倍水平方向的量。
现在让我们从不同的角度理解这个函数。假设𝑎 = 5 ,此时𝑓(𝑎) = 3𝑎 = 15。把𝑎右移一个很小的幅度,增加到 5.001,𝑓(𝑎) = 15.003。 即在𝑎 = 5 时,斜率是 3,这就是表示,当微小改变变量𝑎的值,𝑑𝑓(𝑎)/𝑑𝑎= 3 。一个等价的导数表达式可以这样写 𝑑𝑓(𝑎) /𝑑𝑎,不管你是否将𝑓(𝑎)放在上面或者放在右边都没有关系。
在这个视频中,我讲解导数讨论的情况是我们将𝑎偏移 0.001,如果你想知道导数的数学定义,导数是你右移很小的𝑎值(不是 0.001,而是一个非常非常小的值)。通常导数的定义是你右移𝑎(可度量的值)一个无限小的值,𝑓(𝑎)增加 3 倍(增加了一个非常非常小的值)。也就是这个三角形右边的高度。
那就是导数的正式定义。但是为了直观的认识,我们将探讨右移𝑎 = 0.001 这个值,即使 0.001 并不是无穷小的可测数据。导数的一个特性是:这个函数任何地方的斜率总是等于3,不管𝑎 = 2或 𝑎 = 5,这个函数的斜率总等于 3,也就是说不管𝑎的值如何变化,如果你增加 0.001,𝑓(𝑎)的值就增加 3 倍。这个函数在所有地方的斜率都相等。一种证明方式是无论你将小三角形画在哪里,它的高除以宽总是 3。
我希望带给你一种感觉:什么是斜率?什么是导函数?对于一条直线,在例子中函数的斜率,在任何地方都是 3。在下一个视频让我们看一个更复杂的例子,这个例子中函数在不同点的斜率是可变的。
2.6 更多的导数例子(More Derivative Examples)
在这个视频中我将给出一个更加复杂的例子,在这个例子中,函数在不同点处的斜率是不一样的,先来举个例子:

我在这里画一个函数,𝑓(𝑎) = a 2 a^2 a2,如果𝑎 = 2 的话,那么𝑓(𝑎) = 4。让我们稍稍往右推进一点点,现在𝑎 = 2.001 ,则𝑓(𝑎) ≈ 4.004 (如果你用计算器算的话,这个准确的值应该为 4.004。0.001 我只是为了简便起见,省略了后面的部分),如果你在这儿画,一个小三角形 你就会发现,如果把𝑎往右移动 0.001,那么𝑓(𝑎)将增大四倍,即增大 0.004。在微积分中我们把这个三角形斜边的斜率,称为𝑓(𝑎)在点𝑎 = 2 处的导数(即为 4),或者写成微积分的形式,当𝑎 = 2 的时候, 𝑑𝑓(𝑎)/𝑑𝑎 = 4 由此可知,函数𝑓(𝑎) = 𝑎2,在𝑎取不同值的时候,它的斜率是不同的,这和上个视频中的例子是不同的。
这里有种直观的方法可以解释,为什么一个点的斜率,在不同位置会不同如果你在曲线上,的不同位置画一些小小的三角形你就会发现,三角形高和宽的比值,在曲线上不同的地方,它们是不同的。所以当𝑎 = 2 时,斜率为 4;而当𝑎 = 5时,斜率为 10 。如果你翻看微积分的课本,课本会告诉你,函数𝑓(𝑎) = a 2 a^2 a2的斜率(即导数)为2𝑎。这意味着任意给定一点𝑎,如果你稍微将𝑎,增大 0.001,那么你会看到𝑓(𝑎)将增大2𝑎,即增大的值为点在𝑎处斜率或导数,乘以你向右移动的距离。
现在有个小细节需要注意,导数增大的值,不是刚好等于导数公式算出来的值,而只是根据导数算出来的一个估计值。
为了总结这堂课所学的知识,我们再来看看几个例子:

假设𝑓(𝑎) = a 3 a^3 a3 如果你翻看导数公式表,你会发现这个函数的导数,等于 3 a 2 3a^2 3a2。所以这是什么意思呢,同样地举一个例子:我们再次令𝑎 = 2,所以 a 3 a^3 a3 = 8 ,如果我们又将𝑎增大一点点,你会发现𝑓(𝑎) ≈ 8.012,你可以自己检查一遍,如果我们取 8.012,你会发现2.0013 ,和 8.012 很接近,事实上当𝑎 = 2时,导数值为3 × 2 2 2^2 22,即3 × 4 = 12。所以导数公式,表明如果你将𝑎向右移动 0.001 时,𝑓(𝑎) 将会向右移动 12 倍,即 0.012。
来看最后一个例子,假设𝑓(𝑎) = log𝑒𝑎,有些可能会写作ln𝑎,函数log𝑎 的斜率应该为1/𝑎,所以我们可以解释如下:如果𝑎取任何值,比如又取𝑎 = 2,然后又把𝑎向右边移动 0.001 那么𝑓(𝑎)将增大1/𝑎× 0.001,如果你借助计算器的话,你会发现当𝑎 = 2时𝑓(𝑎) ≈ 0.69315 ;
而𝑎 = 2.001时,𝑓(𝑎) ≈ 0.69365。所以𝑓(𝑎)增大了 0.0005,如果你查看导数公式,当𝑎 = 2的时候,导数值 𝑑𝑓(𝑎) /𝑑𝑎 =1/2。这表明如果你把 增大 0.001,𝑓(𝑎)将只会增大 0.001 的二分之一,即 0.0005。如果你画个小三角形你就会发现,如果𝑥 轴增加了 0.001,那么𝑦 轴上的函
数log𝑎,将增大 0.001 的一半 即 0.0005。所以 1𝑎 ,当𝑎 = 2时这里是 ,就是当𝑎 = 2时这条线的斜率。这些就是有关导数的一些知识。
在这个视频中,你只需要记住两点:
第一点,导数就是斜率,而函数的斜率,在不同的点是不同的。在第一个例子中𝑓(𝑎) =3𝑎 ,这是一条直线,在任何点它的斜率都是相同的,均为 3。但是对于函数𝑓(𝑎) = a 2 a^2 a2 ,或者𝑓(𝑎) = log𝑎,它们的斜率是变化的,所以它们的导数或者斜率,在曲线上不同的点处是不同的。
第二点,如果你想知道一个函数的导数,你可参考你的微积分课本或者维基百科,然后你应该就能找到这些函数的导数公式。
最后我希望,你能通过我生动的讲解,掌握这些有关导数和斜率的知识,下一课我们将讲解计算图,以及如何用它来求更加复杂的函数的导数。
2.7 计算图(Computation Graph)
可以说,一个神经网络的计算,都是按照前向或反向传播过程组织的。首先我们计算出一个新的网络的输出(前向过程),紧接着进行一个反向传输操作。后者我们用来计算出对应的梯度或导数。计算图解释了为什么我们用这种方式组织这些计算过程。在这个视频中,我们将举一个例子说明计算图是什么。让我们举一个比逻辑回归更加简单的,或者说不那么正式的神经网络的例子。
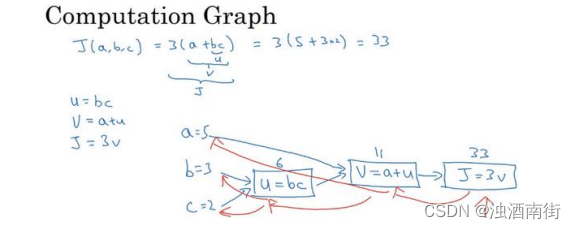
我们尝试计算函数𝐽,𝐽是由三个变量𝑎, 𝑏, 𝑐组成的函数,这个函数是3(a + bc) 。计算这个函数实际上有三个不同的步骤,首先是计算 𝑏 乘以 𝑐,我们把它储存在变量𝑢中,因此𝑢 = 𝑏𝑐; 然后计算𝑣 = 𝑎 + 𝑢;最后输出𝐽 = 3𝑣,这就是要计算的函数𝐽。我们可以把这三步画成如下的计算图,我先在这画三个变量𝑎, 𝑏, 𝑐,第一步就是计算𝑢 = 𝑏𝑐,我在这周围放个矩形框,它的输入是𝑏, 𝑐,接着第二步𝑣 = 𝑎 + 𝑢,最后一步𝐽 =3𝑣。
举个例子: 𝑎 = 5, 𝑏 = 3, 𝑐 = 2 ,𝑢 = 𝑏𝑐就是 6,就是 5+6=11。𝐽是 3 倍的 ,因此。即3 × (5 + 3 × 2)。如果你把它算出来,实际上得到 33 就是𝐽的值。 当有不同的或者一些特殊的输出变量时,例如本例中的𝐽和逻辑回归中你想优化的代价函数𝐽,因此计算图用来处理这些计算会很方便。从这个小例子中我们可以看出,通过一个从左向右的过程,你可以计算出𝐽的值。为了计算导数,从右到左(红色箭头,和蓝色箭头的过程相反)的过程是用于计算导数最自然的方式。
概括一下:计算图组织计算的形式是用蓝色箭头从左到右的计算,让我们看看下一个视频中如何进行反向红色箭头(也就是从右到左)的导数计算,让我们继续下一个视频的学习。
2.8 使用计算图求导数(Derivatives with a Computation Graph)
在上一个视频中,我们看了一个例子使用流程计算图来计算函数𝐽。现在我们看看流程图的描述,看看你如何利用它计算出函数𝐽的导数。
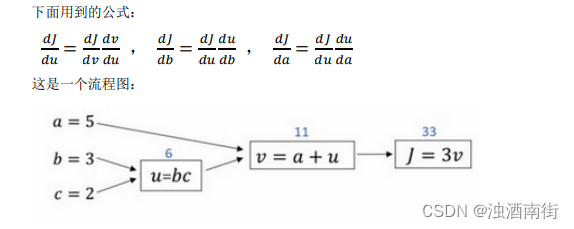
假设你要计算 d J d v \frac{dJ}{dv} dvdJ,那要怎么算呢?好,比如说,我们要把这个𝑣值拿过来,改变一下,那么𝐽的值会怎么变呢?
所以定义上𝐽 = 3𝑣,现在𝑣 = 11,所以如果你让𝑣增加一点点,比如到 11.001,那么𝐽 =3𝑣 = 33.003,所以我这里𝑣增加了 0.001,然后最终结果是𝐽上升到原来的 3 倍,所以 d J d v \frac{dJ}{dv} dvdJ= 3,因为对于任何 𝑣 的增量𝐽都会有 3 倍增量,而且这类似于我们在上一个视频中的例子,我们有𝑓(𝑎) = 3𝑎,然后我们推导出 d d a \frac{d}{da} dad𝑓(𝑎)= 3,所以这里我们有𝐽 = 3𝑣,所以 d J d v \frac{dJ}{dv} dvdJ= 3,这里𝐽扮演了𝑓的角色,在之前的视频里的例子。
在反向传播算法中的术语,我们看到,如果你想计算最后输出变量的导数,使用你最关心的变量对𝑣的导数,那么我们就做完了一步反向传播,在这个流程图中是一个反向步。
我们来看另一个例子, d J d a \frac{dJ}{da} dadJ是多少呢?换句话说,如果我们提高𝑎的数值,对𝐽的数值有什么影响?
好,我们看看这个例子。变量𝑎 = 5,我们让它增加到 5.001,那么对𝑣的影响就是𝑎 + 𝑢,之前𝑣 = 11,现在变成 11.001,我们从上面看到现在𝐽就变成 33.003 了,所以我们看到的是,如果你让𝑎增加 0.001,𝐽增加 0.003。那么增加𝑎,我是说如果你把这个 5 换成某个新值,那么𝑎的改变量就会传播到流程图的最右,所以𝐽最后是 33.003。所以𝐽的增量是 3 乘以𝑎的增量,意味着这个导数是 3。
要解释这个计算过程,其中一种方式是:如果你改变了𝑎,那么也会改变𝑣,通过改变𝑣,也会改变𝐽,所以𝐽值的净变化量,当你提升这个值(0.001),当你把𝑎值提高一点点,这就是𝐽的变化量(0.003)。
首先𝑎增加了,𝑣也会增加,𝑣增加多少呢?这取决于 d v d a \frac{dv}{da} dadv,然后𝑣的变化导致𝐽也在增加,所以这在微积分里实际上叫链式法则,如果𝑎影响到𝑣,𝑣影响到𝐽,那么当你让𝑎变大时,𝐽的变化量就是当你改变𝑎时,𝑣的变化量乘以改变𝑣时𝐽的变化量,在微积分里这叫链式法则。
我们从这个计算中看到,如果你让𝑎增加 0.001,𝑣也会变化相同的大小,所以 d v d a \frac{dv}{da} dadv= 1。事实上,如果你代入进去,我们之前算过 d J d v \frac{dJ}{dv} dvdJ= 3, d v d a \frac{dv}{da} dadv= 1,所以这个乘积 3×1,实际上就给出了正确答案, d J d a \frac{dJ}{da} dadJ= 3。
现在我想介绍一个新的符号约定,当你编程实现反向传播时,通常会有一个最终输出值是你要关心的,最终的输出变量,你真正想要关心或者说优化的。在这种情况下最终的输出变量是𝐽,就是流程图里最后一个符号,所以有很多计算尝试计算输出变量的导数,所以输出变量对某个变量的导数,我们就用𝑑𝑣𝑎𝑟命名,所以在很多计算中你需要计算最终输出结果的导数,在这个例子里是𝐽,还有各种中间变量,比如𝑎、𝑏、𝑐、𝑢、𝑣,当你在软件里实现的时候,变量名叫什么?你可以做的一件事是,在 python 中,你可以写一个很长的变量名,比如𝑑𝐹𝑖𝑛𝑎𝑙𝑂𝑢𝑡𝑝𝑢𝑡𝑣𝑎𝑟_𝑑𝑣𝑎𝑟,但这个变量名有点长,我们就用𝑑𝐽_𝑑𝑣𝑎𝑟,但因为你一直对𝑑𝐽求导,对这个最终输出变量求导。我这里要介绍一个新符号,在程序里,当你编程的时候,在代码里,我们就使用变量名𝑑𝑣𝑎𝑟,来表示那个量。
好,所以在程序里是𝑑𝑣𝑎𝑟表示导数,你关心的最终变量𝐽的导数,有时最后是𝐿,对代码中各种中间量的导数,所以代码里这个东西,你用𝑑𝑣表示这个值,所以𝑑𝑣 = 3,你的代码表示就是𝑑𝑎 = 3。
好,所以我们通过这个流程图完成部分的后向传播算法。我们在下一张幻灯片看看这个例子剩下的部分。
我们清理出一张新的流程图,我们回顾一下,到目前为止,我们一直在往回传播,并计算𝑑𝑣 = 3,再次,𝑑𝑣是代码里的变量名,其真正的定义是 d J d v \frac{dJ}{dv} dvdJ。我发现𝑑𝑎 = 3,再次,𝑑𝑎是代码里的变量名,其实代表 d J d a \frac{dJ}{da} dadJ的值。
同理我们可以计算出
d b = d J d b = d J d v d v d u d u d b = 3 ∗ 1 ∗ c = 3 ∗ 1 ∗ 2 = 6 db=\frac{dJ}{db} =\frac{dJ}{dv} \frac{dv}{du} \frac{du}{db} =3*1*c =3*1*2 =6 db=dbdJ=dvdJdudvdbdu=3∗1∗c=3∗1∗2=6
d c = d J d c = d J d v d v d u d u d c = 3 ∗ 1 ∗ b = 3 ∗ 1 ∗ 3 = 9 dc=\frac{dJ}{dc} =\frac{dJ}{dv} \frac{dv}{du} \frac{du}{dc} =3*1*b =3*1*3=9 dc=dcdJ=dvdJdudvdcdu=3∗1∗b=3∗1∗3=9
相关文章:

吴恩达深度学习笔记:神经网络的编程基础2.5-2.8
目录 第一门课:神经网络和深度学习 (Neural Networks and Deep Learning)第二周:神经网络的编程基础 (Basics of Neural Network programming)2.5 导数(Derivatives)2.6 更多的导数例子(More Derivative Examples&…...
iphoneX系统的参数
1. 2. 3. 4. 5.相关的网址信息 Apple iPhone X 規格、价格和评论 | Kalvo Apple iPhone X 規格、价格和评论 | Kalvo...
基于云计算的前端资源管理系统的设计与实现
hello宝子们...我们是艾斯视觉擅长ui设计和前端开发10年经验!希望我的分享能帮助到您!如需帮助可以评论关注私信我们一起探讨!致敬感谢感恩! 随着互联网的快速发展,前端资源管理成为了一个重要的课题。本文旨在设计并实…...
区块链技术与大数据结合的商业模式探索
hello宝子们...我们是艾斯视觉擅长ui设计和前端开发10年经验!希望我的分享能帮助到您!如需帮助可以评论关注私信我们一起探讨!致敬感谢感恩! 随着区块链技术和大数据技术的不断发展,两者的结合为企业带来了新的商业模式…...
基于JavaSpringboot+Vue实现前后端分离房屋租赁系统
基于JavaSpringbootVue实现前后端分离房屋租赁系统 博主介绍:多年java开发经验,专注Java开发、定制、远程、文档编写指导等,csdn特邀作者、专注于Java技术领域 作者主页 央顺技术团队 Java毕设项目精品实战案例《1000套》 欢迎点赞 收藏 ⭐留言 文末获取…...

Yarn: 安装与使用教程
Yarn是Facebook开发的一款高效、可靠的包管理器,用于JavaScript项目中依赖项的管理和版本控制。它作为npm(Node.js包管理器)的一个替代品,提供了更快的安装速度、更安全的依赖管理以及更好的协作体验。以下是Yarn的安装步骤以及基…...
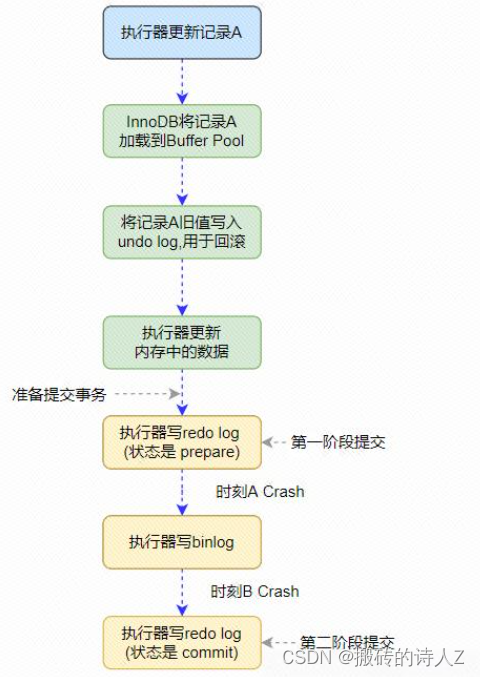
数据库是怎么做到事务回滚的呢?
数据库实现事务回滚的原理涉及到数据库管理系统(DBMS)如何维护事务的一致性和持久性。 基本原理: ACID属性:事务的原子性(Atomicity)、一致性(Consistency)、隔离性(Iso…...

海思 Hi3519DV500 简介
海思 Hi3519DV500 简介 Hi3519DV500是一颗面向视觉行业推出的超高清智能 SoC。最高支持四路sensor输入,支持最高4K30fps的ISP图像处理能力。支持 2F WDR、多级降噪、六轴防抖、全景拼接、多光谱融合等多种传统图像增强和处理算法。支持越影AI ISP全天候卓越影像&am…...

盘点全球十大FPGA制造商
1. 赛灵思(Xilinx) 赛灵思是全球领先的FPGA供应商,市场份额超过50%。公司成立于1984年,总部位于加利福尼亚州圣何塞。关于赛灵思的一些重要事实: 提供业界最广泛的 FPGA 产品组合,包括 UltraScale、UltraS…...
)
【MySQL】14. 全文索引(选学)
全文索引的创建 当对文章字段或有大量文字的字段进行检索时,会使用到全文索引。 MySQL提供全文索引机制,但是有要求,要求表的存储引擎必须是MyISAM,而且默认的全文索引支持英文,不支持中文。 (为啥一定要用MyISAM呢&am…...
C++实现FFmpeg音视频实时拉流并播放
1.准备工作: 下载rtsp流媒体服务器rtsp-simple-server,安装go开发环境并编译 编译好后启动流媒体服务器 准备一个要推流的mp4视频文件,如db.mp4 使用ffmpeg开始推流 推流命令: ffmpeg -re -stream_loop -1 -i db.mp4 -c copy -rtsp_transport tcp -f rtsp rtsp://192.168.16…...
国内ip切换app,让切换ip变得简单
在数字化快速发展的今天,互联网已经成为我们生活中不可或缺的一部分。然而,随着网络应用的深入,用户对于网络环境的需求也日益多样化。其中,IP地址作为网络中的关键标识,其切换与管理显得尤为重要。为了满足用户对于IP…...
阿里云倚天服务器是什么?倚天服务器c8y、g8y和r8y详细介绍
阿里云倚天云服务器CPU采用倚天710处理器,租用倚天服务器c8y、g8y和r8y可以享受优惠价格,阿里云服务器网aliyunfuwuqi.com整理倚天云服务器详细介绍、倚天710处理器性能测评、CIPU架构优势、倚天服务器使用场景及生态支持: 阿里云倚天云服务…...

ip地址开发场景问题
这种问题一般是出现在我们的项目日志中,可能想去收集某一个时间段内,或者说时某一个时间点的ip地址,或者说是想从大量数据中,选出ip地址出现次数最多的ip。大概是分为这几个问题。 1.亿万级数据中如何快速取出某一天的ip地址。 这…...

【功能实现】新年贺卡(蓝桥)
题目分析: 想要实现一个随机抽取功能 功能拆解:题目给了数组,我们采用生成随机数的方式,随机数作为数组的索引值访问数组的值。 并返回获取到的值,将获取到的值插入到页面中。 document.addEventListener(DOMConten…...
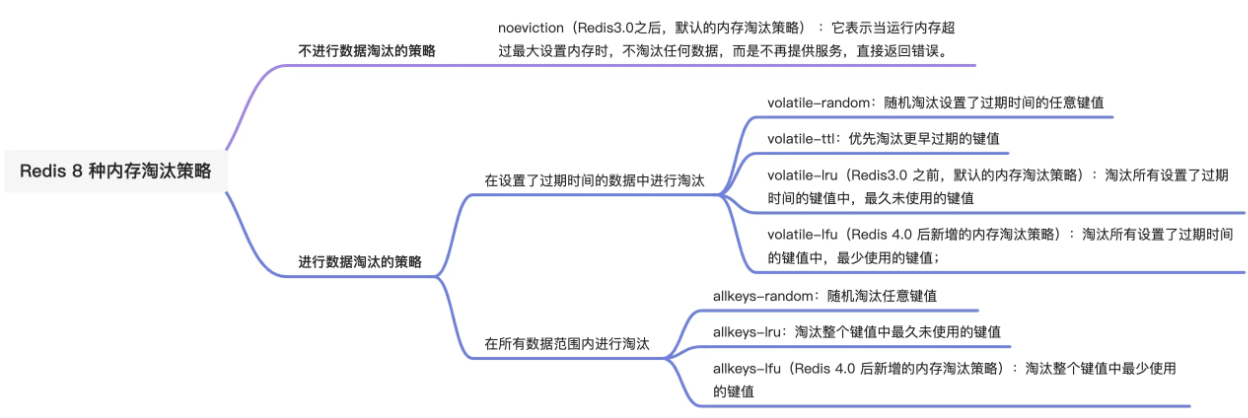
【Redis教程0x08】详解Redis过期删除策略内存淘汰策略
引言 Redis的过期删除策略和内存淘汰策略是经常被问道的问题,这两个机制都是做删除操作,但是触发的条件和使用的策略是不同的。今天就来深入理解一下这两个策略。 过期删除策略 Redis 是可以对 key 设置过期时间的,因此需要有相应的机制将…...

鸿蒙开发 TypeScript 基础语法
文章的最下面有官网链接可以进行练习! 变量声明 TypeScript 在 JavaScript 的基础上加入了静态类型检查功能,因此每一个变量都有固定的数据类型 let:声明变量的关键字,const则代表常量 示例代码: // string&#…...

uniapp 未配置appkey或配置错误的解决
报错解决:未配置appkey或配置错误 首先:HbuilderX Android sdk 3.1.10版本起需要申请Appkey 配置Appkey:打开Androidmanifest.xml, 导航到Application节点,创建meta-data节点,name为dcloud_appkey&#x…...
)
【Android】【Bluetooth Stack】蓝牙电话协议之拨打电话分析(超详细)
1. 精讲蓝牙协议栈(Bluetooth Stack):SPP/A2DP/AVRCP/HFP/PBAP/IAP2/HID/MAP/OPP/PAN/GATTC/GATTS/HOGP等协议理论 2. 欢迎大家关注和订阅,【蓝牙协议栈】和【Android Bluetooth Stack】专栏会持续更新中.....敬请期待! 目录 1. 协议架构 1.1 Profile Dependencies...
记录关于智能家居的路程的一个bug___Segmentation fault(段错误)
前言 其实发生段错误的情况有很多: 其实在项目的开发中最有可能的错误就是①和②,考虑到本项目数组用的比较少,所以主要是考虑错误①指针的误用。 有时候错误就是那么离谱,声音也算是一种设备??ÿ…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...
