【数据结构与算法】快速排序(详解:快排的Hoare原版,挖坑法和双指针法|避免快排最坏时间复杂度的两种解决方案|小区间优化|非递归的快排)

引言
快速排序作为交换排序的一种,在排序界的影响力毋庸置疑,我们C语言中用的qsort,C++中用的sort,底层的排序方式都是快速排序。相比于同为交换排序的冒泡,其效率和性能就要差的多了,本篇博客就是要重点介绍快速排序的实现,以及其代码和效率的优化。
话不多说,开始我们今天的内容。
快速排序的基本逻辑
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法,其基本思想为:任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,使左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
用通俗的语言讲:
- 从一组元素序列中(称这个序列为A0)随机取出一个数,我们可以称这个数为k
- 将比k元素小的数放在k的左边,比k元素大的数放在k的右边
- 此时分别将K左右两边边的元素,拿出来各成一个序列(称为A1和A2)
- 同样用处理A的方式处理A1,A2序列
最后,序列中所有左边的数都会比右边的小,完成快速排序。
可以先来处理第一步和第二步,也就是快速排序的第一层排序。
快速排序的第一层
这里有一张gif动图,大家可以先预热一下,如果看懂了,可以跳过一部分的讲解。

第一步,取第一个元素(下标为key)为基准值,我们的目的是使基准值左边的数都比基准值小,基准值右边的数都比基准值大。
第二步,定义两个下标变量,一个变量从右往左走(R),一个变量左往右走(L)。首先从R开始往左走(走的时候左边的L保持不动),每走一步都与基准值相比较。
让 R 停下来的条件有两个:① R 位置的值比基准值小。 ② R 与 L 相遇。
第三步,如果让R停下来的条件为①,则L开始往右一步步走,每走一步也都与基准值比较。
让 L 停下来的条件也有两个:① L 位置的值比基准值大。 ② R 与 L 相遇。
第四步,如果让 L 停下来的条件为①,则交换 L 和 R 两位置所存的值,回到第二步, R 开始往左移动,重复此过程,直到 L 和 R 相遇。
在整个四步过程中,一旦出现 R 和 L 相遇,则第一层数据遍历结束,交换 L 和基准值key存的值并进入下一层的排序。
注:在第二步的时候要统一由 R 先开始移动,这样可以保证在L和R相遇时一定会是比key小的数。这是因为R先移动,在找到比基准值小的数前是不会停止的;而L移动的前提条件是R找到了比基准值小的数(这一特性使R静止的位置一定会是比基准值key小的数)。
故:L和R静止一方的值必定比基准值key小。
关于L和R相遇时一定会是比key小的数这个问题如果还没搞懂,可以拿张纸来画一画。
上面就是一层快速排序的全过程,在这一层排序过后,可以找到一个基准值的真正位置,也让基准值左边的数都小,右边的数都大。
接下来是这一层排序的代码实现:
void Swap(int* x, int* y)
{int tmp = *x;*x = *y;*y = tmp;
}int left = 0, right = n - 1;
int keyi = 0;
while (left < right) {while (right > left && a[right] >= a[keyi]) {right--;}while (right > left && a[left] <= a[keyi]){left++;}Swap(&a[left], &a[right]);
}
Swap(&a[keyi], &a[left]);递归版快速排序的实现
Hoare版快速排序
写完了第一层之后,其他的工作就轻松多了,就是运用递归,每层递归时,需要调整left和right的值。这个过程和二叉树的前序遍历非常相似,以下就是完整的hoare版的快速排序:
void Swap(int* x, int* y)
{int tmp = *x;*x = *y;*y = tmp;
}void QuickSort1(int* a, int left, int right)
{//当left>=right时递归结束if (left >= right)return;int begin = left, end = right;int keyi = left;while (left < right) {while (right > left && a[right] >= a[keyi]) {right--;}while (right > left && a[left] <= a[keyi]) {left++;}Swap(&a[left], &a[right]);}Swap(&a[keyi], &a[left]);QuickSort1(a, begin, left - 1);QuickSort1(a, left + 1, end);
}在递归的过程中,递归的第一个区间是:[begin , left - 1(left - 1即相遇的前一个位置) ],递归的第二个区间:[left + 1(left + 1即相遇的后一个位置) , end]

在快速排序的递归实现中,除了发明快速排序的大佬hoare的原版排序方式。还有两种方式,虽然底层原理都是一样的,但这两种方式也有各自的特点。
挖坑法快速排序
什么是挖坑法,顾名思义,就是挖一个坑。在理解了hoare版本快速排序的基础上理解这个方式并不困难,下面来看看挖坑法的gif格式动图:

第一步,将基准值挖出存在key中,基准值位置下标用一个变量hole位记录(相当于一个坑位)
第二步,首先从R开始往左走(走的时候左边的L保持不动),每走一步都与基准值相比较。
让 R 停下来的条件有两个:① R 位置的值比基准值小。 ② R 与 L 相遇。
第三步,如果使R停下来的条件为①,则将R下标位置的值放入坑位hole中,同时将R下标赋给hole,这时候坑位变成R的位置。
第四步,如果让R停下来的条件为①,则L开始往右一步步走,每走一步也都与基准值比较。
让 L 停下来的条件也有两个:① L 位置的值比基准值大。 ② R 与 L 相遇。
第五步,如果使L停下来的条件为①,则将L下标的值放入hole中,同时将L下标赋给hole,这时候坑位变成L的位置。
这里遍历停止的标志也同样是L和R相遇,相遇的位置也是一个坑位,直接把key的值放到坑位中,第一层整个数据处理就结束了。
下面是挖坑法的实现代码:
void Swap(int* x, int* y)
{int tmp = *x;*x = *y;*y = tmp;
}void QuickSort2(int* a, int left, int right)
{if (left >= right)return;int begin = left, end = right;int valk = a[left]; int holei = left;while (left < right) {while (right > left && a[right] >= valk) {right--;}a[holei] = a[right]; holei = right;while (right > left && a[left] <= valk) {left++;}a[holei] = a[left];holei = left;}a[holei] = valk;QuickSort2(a, begin, left - 1);QuickSort2(a, left + 1, end);
}挖坑法的优势在于好理解,就是保持一个坑位,不断往里面填数字然后变换坑位的过程。
前后指针版快速排序
前后指针版本的快速排序不好理解,但是代码量出奇的少,先看一下gif动图了解大致思路:

规则很简单:
- cur >= key ,++cur
- cur < key ,++prev ,交换prev和cur的值
- 结束条件:cur > end
- 结束后,交换prev和key的值
在整个过程中,prev的位置之前的数据都小于基准值key,而prev和cur之间的值都保证大于基准值key,在prev和cur的值交换的过程中,相当于把大的数字往后甩,把cur找到的小的值往前插入。在cur遍历到最后,比基准值小的数字也就成功都插入到了前面,而比基准值大的数字也都被甩到了后面。这时交换prev和key的值也就达到了快速排序第一层遍历后的效果。
下面是前后针法的实现代码:
void Swap(int* x, int* y)
{int tmp = *x;*x = *y;*y = tmp;
}void QuickSort3(int* a, int left, int right)
{if (right <= left)return;int pcur = left + 1, prev = left, keyi = left;while (pcur <= right) { if (a[pcur] < a[keyi] && ++prev != pcur) Swap(&a[pcur], &a[prev]);++pcur;}Swap(&a[keyi], &a[prev]);QuickSort3(a, left, prev - 1);QuickSort3(a, prev + 1, right);
}建议大家可以把前后指针法的实现理解后背下来,后期Hr面试问的时候搓起来会很爽。
避免最坏时间复杂度的两种解决方案
快速排序排起来是很快,但我们上面所写的快排真的就没有缺陷吗?
现在你可以试想一种场景,如果用上面所写的代码去排一个有序数组会如何。
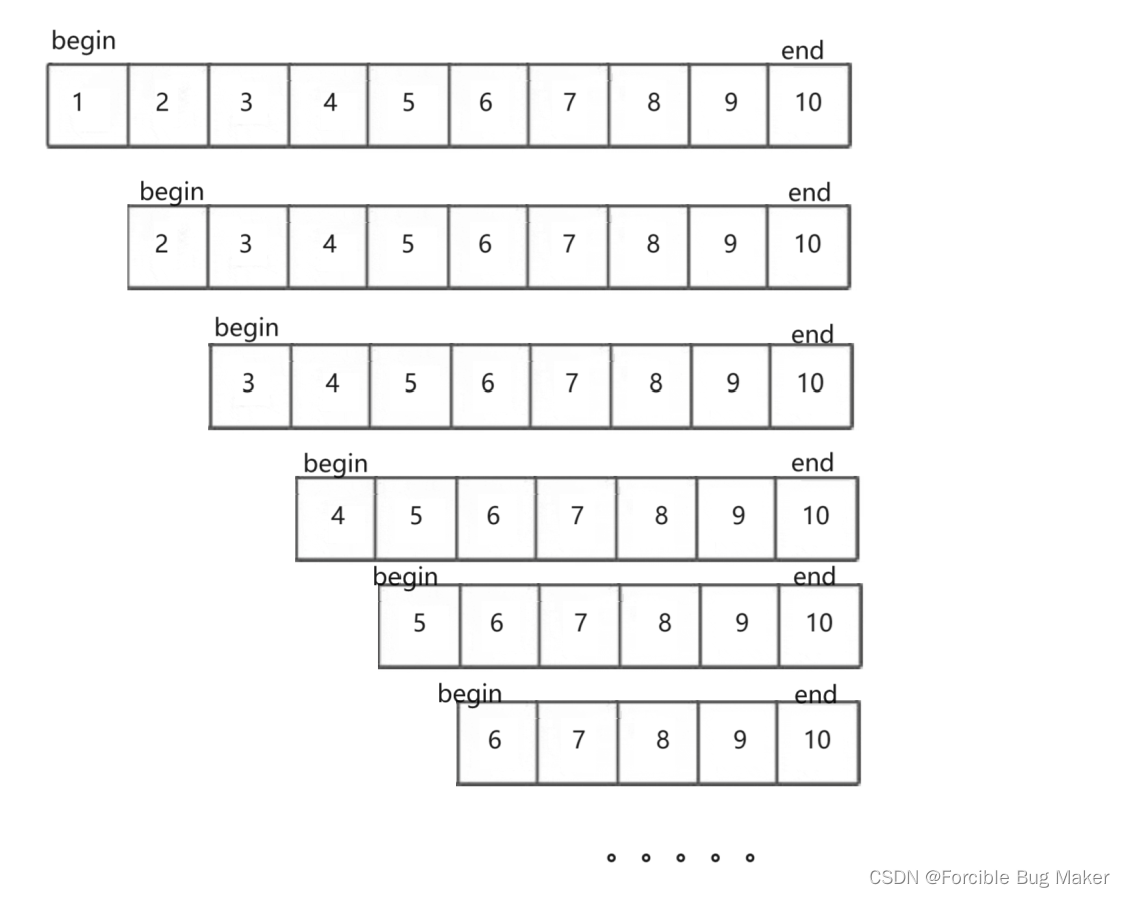
这时候的复杂度将会是一场灾难。基准值如果每次都是数组的第一个值,那么这种情况就很有可能会出现。对于这种由于顺序引起的最坏时间复杂度问题,这里提供两种解决方案。
1.随机选key
既然害怕数组顺序无法选出随机数,那么让选的基准值下标值为随机取的不就能解决问题了吗?就是我们所说的随机选key。
这里随机数需要用到rand()函数,头文件<stdlib.h>
int randi = rand();
randi %= (right - left + 1);
randi += left;
Swap(&a[randi], &a[left]);以上就是随机key的取法,(right - left + 1) 是为了控制范围防止越界对随机数做的一个处理。
把这种处理方式放入快排代码中就是这个样子,以Hoare版为例:
void Swap(int* x, int* y)
{int tmp = *x;*x = *y;*y = tmp;
}void QuickSort1(int* a, int left, int right)
{//当left>=right时递归结束if (left >= right)return;int begin = left, end = right;int keyi = left;//取随机key部分int randi = rand();randi %= (right - left + 1);randi += left;Swap(&a[randi], &a[left]);//-----------while (left < right) {while (right > left && a[right] >= a[keyi]) {right--;}while (right > left && a[left] <= a[keyi]) {left++;}Swap(&a[left], &a[right]);}Swap(&a[keyi], &a[left]);QuickSort1(a, begin, left - 1);QuickSort1(a, left + 1, end);
}2.三数取中
具体思路是,找三个下标left,right ,mid对应的数,取三个数中处于中间位置的作为key(基准值),其中 mid = (left + right) / 2 。
这里我们专们写一个三数取中的函数,这一过程相对比较复杂:
//三数取中函数
int GetMid(int* a, int left, int right)
{int mid = (left + right) / 2;if (a[left] < a[mid]) {if (a[mid] < a[right])return mid;else if (a[left] > a[right])return left;else return right;}else {if (a[mid] > a[right])return mid;else if (a[left] > a[right])return left;else return right;}
}与上述随机取key时放置的位置一样
void Swap(int* x, int* y)
{int tmp = *x;*x = *y;*y = tmp;
}void QuickSort1(int* a, int left, int right)
{//当left>=right时递归结束if (left >= right)return;int begin = left, end = right;int keyi = left;//三数取中部分int midi = GetMid(a, left, right);Swap(&a[midi], &a[left]);//-----------while (left < right) {while (right > left && a[right] >= a[keyi]) {right--;}while (right > left && a[left] <= a[keyi]) {left++;}Swap(&a[left], &a[right]);}Swap(&a[keyi], &a[left]);QuickSort1(a, begin, left - 1);QuickSort1(a, left + 1, end);
}到这里,避免最坏时间复杂度的两种方案就介绍完了。
小区间优化
什么是小区间优化?
你是否考虑过这样一个问题,当快排递归到最后几层时,会产生多少小区间。
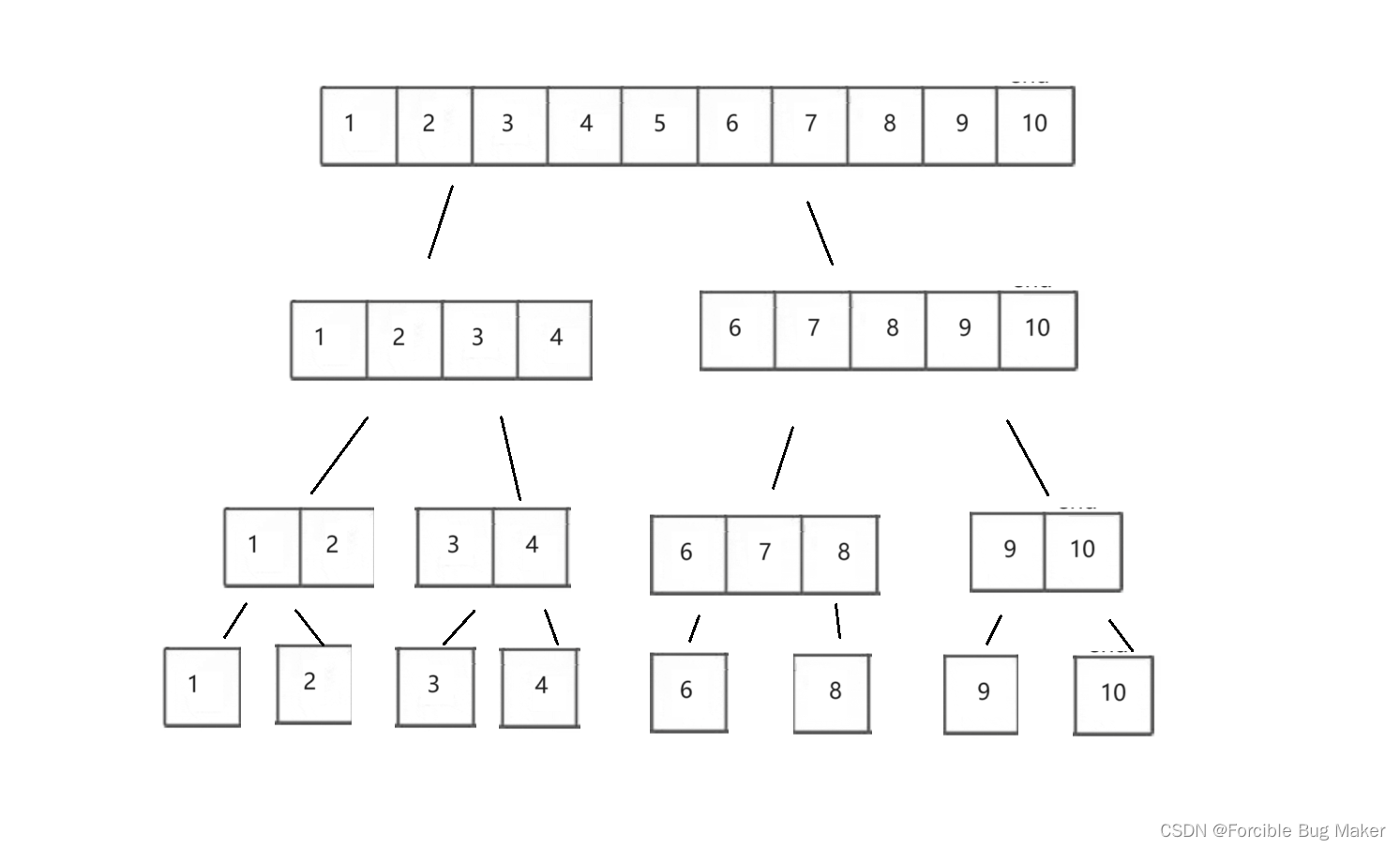
这里出现了一个很明显的问题:待排序的数很少,但是走递归的消耗较大,最后几层的递归占整个递归的80%~90%。
这里给出的小区间优化方式就是,当递归进入待排序数字只剩10个左右的时候,使用直接插入排序的方式对小区间进行排序。
//小区间优化方式
if(right - left + 1 < 10)
{//插入排序,减少90%的递归InsertSort(a + left, right - left + 1);
}放到hoare版快排中就是这样的,可以省去if判断return。
void Swap(int* x, int* y)
{int tmp = *x;*x = *y;*y = tmp;
}void QuickSort1(int* a, int left, int right)
{//小区间优化方式if(right - left + 1 < 10){//插入排序,减少90%的递归InsertSort(a + left, right - left + 1);}//-------------int begin = left, end = right;int keyi = left;while (left < right) {while (right > left && a[right] >= a[keyi]) {right--;}while (right > left && a[left] <= a[keyi]) {left++;}Swap(&a[left], &a[right]);}Swap(&a[keyi], &a[left]);QuickSort1(a, begin, left - 1);QuickSort1(a, left + 1, end);
}此方式优化了大部分的递归,但得益于计算机对递归的处理,这种优化和原版的效率比起来就没有那么明显了。
快速排序的非递归实现
讲了这么多,总算是到了咱们的最后一个问题,快速排序非递归的实现。既然不让递归,咱们可以换个思路,用栈模拟个递归不就行了。在栈中存放左右区间,可以和递归达到同一个效果。
你问我栈是什么?emm,我之前写了一遍关于栈的博客,供参考:
初阶数据结构之---栈和队列(C语言)
取区间的方式:

先插入总区间,进入一个大循环中,循环结束的条件为栈为空,每次取栈顶弹栈,处理区间后再次往栈中插入被分割出来的有效区间,继续循环。
主体思路就是用栈模拟一个递归的过程,栈本来应该是构建一个结构体存左右区间,不过这里我就直默认顺序接插入右区间和左区间,取的时候依次就是是左区间和右区间,不再麻烦造个结构体了。
以下是非递归实现快速排序,复用上次栈的代码:
typedef int STDataType;
typedef struct stack
{STDataType* a;int top;int capacity;
}ST;void STInit(ST* ps)
{assert(ps);ps->a = NULL;ps->top = ps->capacity = 0;
}void STDestory(ST* ps)
{assert(ps);free(ps->a);ps->a = NULL;ps->top = ps->capacity = 0;
}void STPush(ST* ps, STDataType x)
{assert(ps);if (ps->top == ps->capacity) {int newcapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;STDataType* tmp = (STDataType*)realloc(ps->a, newcapacity * sizeof(STDataType));if (tmp == NULL) {perror("realloc tmp fail:");exit(1);}ps->a = tmp;ps->capacity = newcapacity;}ps->a[ps->top] = x;++ps->top;
}bool STEmpty(ST* ps)
{assert(ps);return ps->top == 0;
}void STPop(ST* ps)
{assert(ps);assert(!STEmpty(ps));ps->top--;
}STDataType STTop(ST* ps)
{assert(ps);assert(!STEmpty(ps));return ps->a[ps->top - 1];
}int STSize(ST* ps)
{assert(ps);return ps->top;
}// 快速排序 非递归实现
void QuickSortNonR(int* a, int left, int right)
{ST st;STInit(&st);STPush(&st, right);STPush(&st, left);while (!STEmpty(&st)) {int begin = STTop(&st); STPop(&st);int end = STTop(&st); STPop(&st);if (begin >= end)continue;int keyi = begin, prev = begin, pcur = begin + 1;while (pcur <= end) {if (a[pcur] < a[keyi] && ++prev != pcur)Swap(&a[prev], &a[pcur]);++pcur;}Swap(&a[prev], &a[keyi]);STPush(&st, prev - 1); STPush(&st, begin);STPush(&st, end); STPush(&st, prev + 1);}
}
结语
以上就是快速排序的所有内容,本篇博客关于快排的内容,讲到了Hoare原版快速排序,挖坑法和双指针法,避免快排最坏时间复杂度的两种解决方案,小区间优化,非递归的快排等内容,希望能帮助大家快速理解和学会快速排序。
感谢大家的支持!
相关文章:

【数据结构与算法】快速排序(详解:快排的Hoare原版,挖坑法和双指针法|避免快排最坏时间复杂度的两种解决方案|小区间优化|非递归的快排)
引言 快速排序作为交换排序的一种,在排序界的影响力毋庸置疑,我们C语言中用的qsort,C中用的sort,底层的排序方式都是快速排序。相比于同为交换排序的冒泡,其效率和性能就要差的多了,本篇博客就是要重点介绍…...

三位数组合-第12届蓝桥杯选拔赛Python真题精选
[导读]:超平老师的Scratch蓝桥杯真题解读系列在推出之后,受到了广大老师和家长的好评,非常感谢各位的认可和厚爱。作为回馈,超平老师计划推出《Python蓝桥杯真题解析100讲》,这是解读系列的第42讲。 三位数组合&#…...

Mongodb入门到入土,安装到实战,外包半年学习的成果
这是我参与「第四届青训营 」笔记创作活动的的第27天,今天主要记录前端进阶必须掌握内容Mongodb数据库,从搭建环境到运行数据库,然后使用MongodB; 一、文章内容 数据库基础知识关系型数据库和非关系型数据库为什么学习Mongodb数据库环境搭建及运行MongodbMongodb命…...

【C++初阶】之类和对象(下)
【C初阶】之类和对象(下) ✍ 再谈构造函数🏄 初始化列表的引入💘 初始化列表的语法💘 初始化列表初始化元素的顺序 🏄 explicit关键字 ✍ Static成员🏄 C语言中的静态变量🏄 C中的静…...
Spring Boot 3 极速搭建OAuth2认证框架
本篇环境 Java 17Spring Boot 3.2.3Spring Authorization Server 1.2.3开发工具 SpringToolSuite4Spring Boot 3.2.3 需要JDK 17及之上的版本。 项目初始化 项目可以使用Spring的初始化器生成, 也可以创建一个Maven类型的项目。 项目创建后的目录结构如下: 项目配置 使用 …...
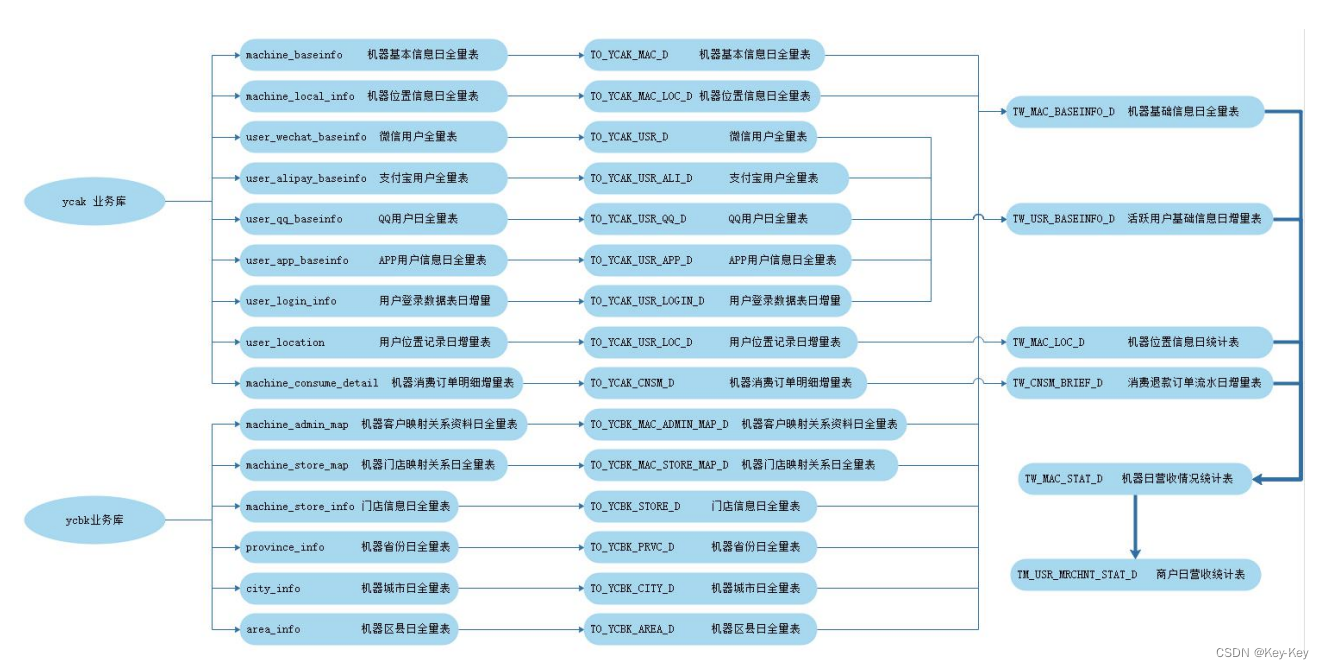
大数据开发(离线实时音乐数仓)
大数据开发(离线实时音乐数仓) 一、数据库与ER建模1、数据库三范式2、ER实体关系模型 二、数据仓库与维度建模1、数据仓库(Data Warehouse、DW、DWH)1、关系型数据库很难将这些数据转换成企业真正需要的决策信息,原因如…...

Python读取csv文件入Oracle数据库
在Python中,使用pandas库的read_sql_query函数可以直接从SQL查询中读取数据到DataFrame。而pd.set_option函数用于设置pandas的显示选项。具体来说,display.unicode.ambiguous_as_wide选项用于控制当字符宽度不明确时,pandas是否将这些字符显…...

Linux_进程概念_冯诺依曼_进程概念_查看进程_获取进程pid_创建进程_进程状态_进程优先级_环境变量_获取环境变量三种方式_3
文章目录 一、硬件-冯诺依曼体系结构二、软件-操作系统-进程概念0.操作系统做什么的1.什么叫做进程2.查看进程3.系统接口 获取进程pid- getpid4.系统接口 获取父进程pid - getppid5.系统接口 创建子进程 - fork1、手册2、返回值3、fork做了什么4、基本用法 6.进程的状态1、进程…...
Set A Light 3D Studio中文--- 打造专业级3D照明效果
Set A Light 3D Studio是一款专业的灯光模拟软件,专为摄影师和电影制片人打造。它允许用户在计算机上模拟并预览各种布光效果,助力拍摄出真实、精准且具有艺术感的作品。软件提供了丰富的灯光和场景模型,用户可以灵活调整光源参数,…...
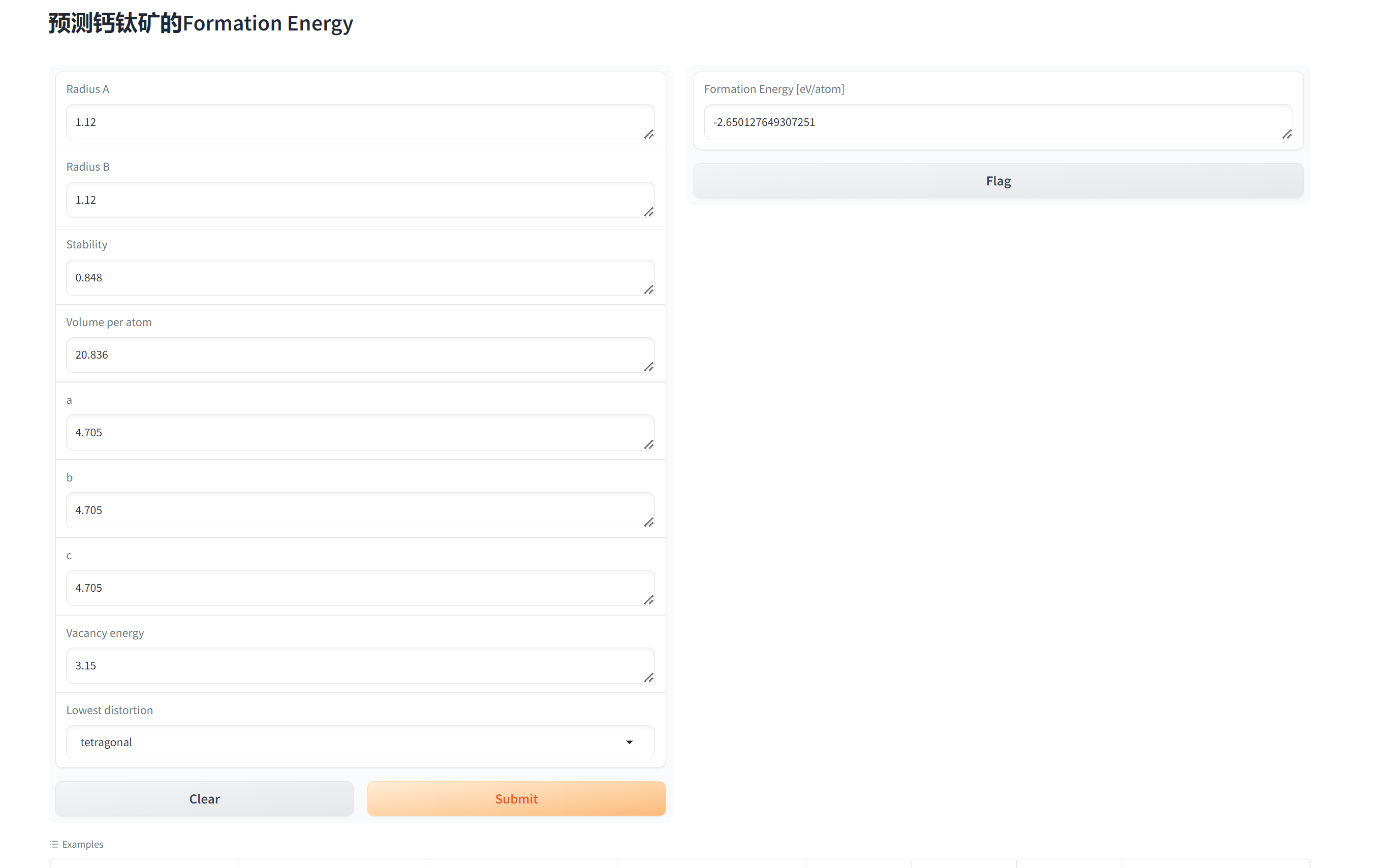
【深度学习】基于机器学习的无机钙钛矿材料形成能预测,预测形成能,神经网络,回归问题
文章目录 任务分析数据处理处理离散数值处理缺失值处理不同范围的数据其他注意事项 我们的数据处理模型训练网页web代码、指导 任务分析 简单来说,就是一行就是一个样本,要用绿色的9个数值,预测出红色的那1个数值。 数据处理 在进行深度数…...
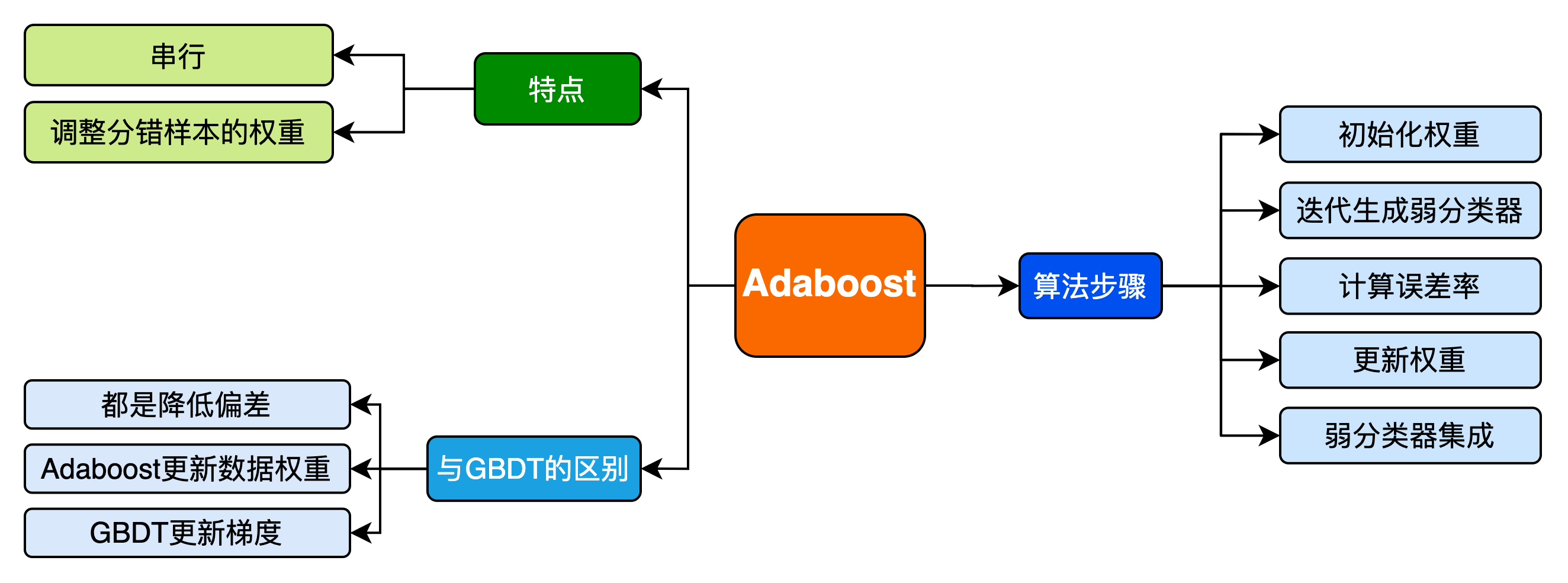
20240321-2-Adaboost 算法介绍
Adaboost 算法介绍 1. 集成学习 集成学习(ensemble learning)通过构建并结合多个学习器(learner)来完成学习任务,通常可获得比单一学习器更良好的泛化性能(特别是在集成弱学习器(weak learner…...
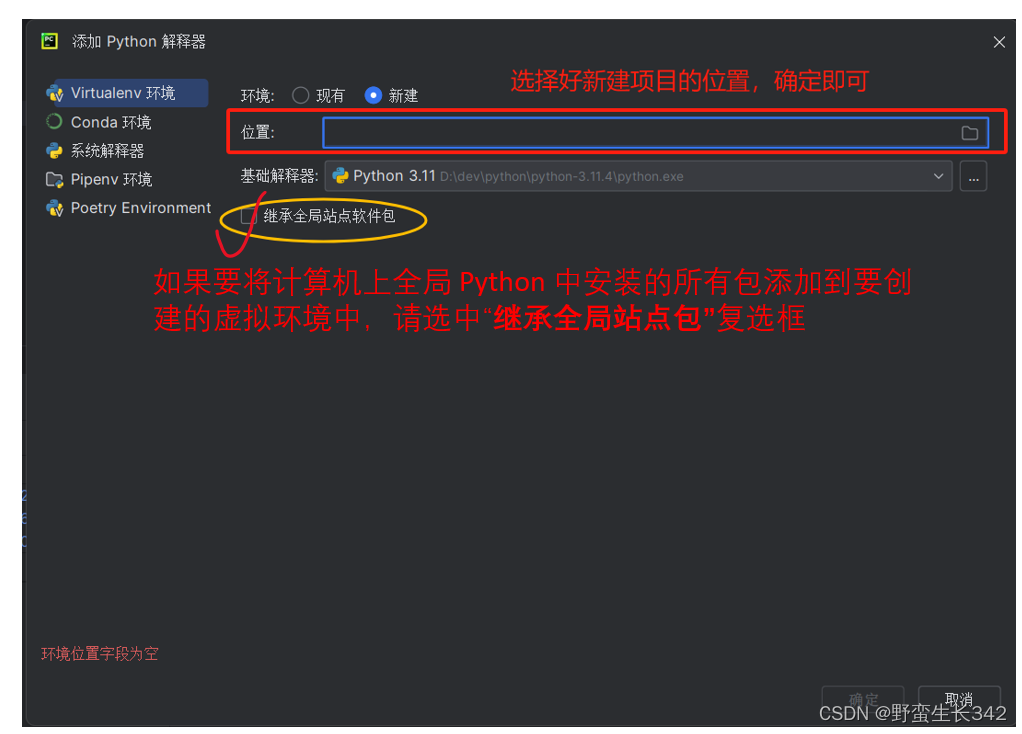
python第三方库的安装,卸载和更新,以及在cmd下pip install安装的包在pycharm不可用问题的解决
目录 第三方库pip安装,卸载更新 1.安装: 2.卸载 3.更新 一、第三方库pip安装,卸载更新 1.安装 pip install 模块名 加镜像下载:pip install -i 镜像网址模块名 常用的是加清华镜像,如 pip install -i https://pyp…...
Python第三次作业
周六 1. 求一个十进制的数值的二进制的0、1的个数 def er(x):a bin(x)b str(a).count("1")c str(a).count("0") - 1print(f"{a},count 1:{b},count 0:{c}")x int(input("enter a number:")) er(x) 2. 实现一个用户管理系统&…...

ai写作软件选哪个?这5款风靡全球的工具不容错过!
从去年到现在,ai 人工智能的发展一直是许多人关注的重点,每隔一段时间新诞生的 ai 工具软件,总会成为人们茶余饭后谈论的焦点。不过在种类繁多的 ai 工具软件中,ai 写作软件是最常被使用的 ai 工具类别,它的使用门槛较…...
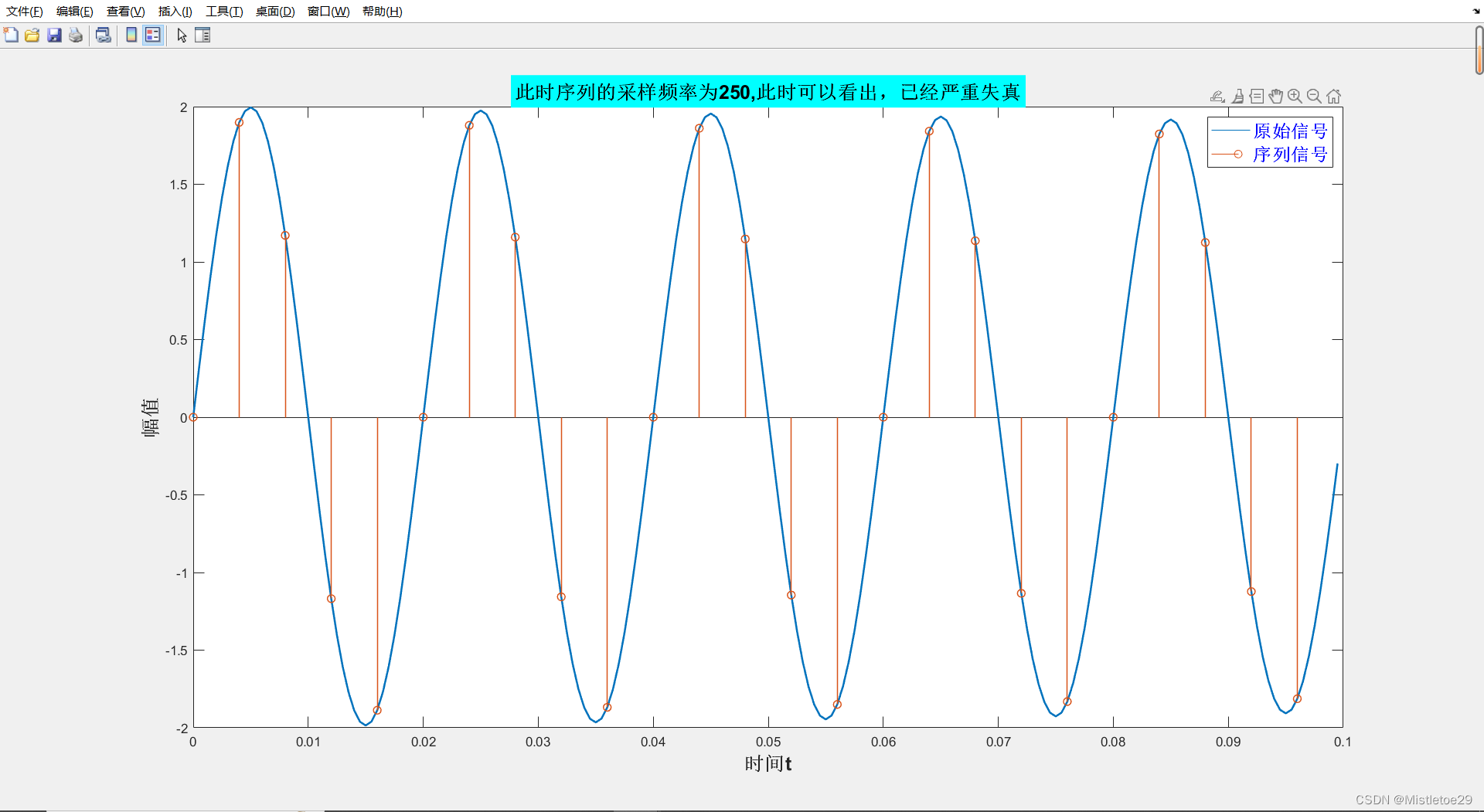
信号处理与分析——matlab记录
一、绘制信号分析频谱 1.代码 % 生成测试信号 Fs 3000; % 采样频率 t 0:1/Fs:1-1/Fs; % 时间向量 x1 1*sin(2*pi*50*t) 1*sin(2*pi*60*t); % 信号1 x2 1*sin(2*pi*150*t)1*sin(2*pi*270*t); % 信号2% 绘制信号图 subplot(2,2,1); plot(t,x1); title(信号x1 1*sin(…...

Android Databinding 使用教程
Android Databinding 使用教程 一、介绍 Android Databinding 是 Android Jetpack 的一部分,它允许你直接在 XML 布局文件中绑定 UI 组件到数据源。通过这种方式,你可以更简洁、更直观地更新 UI,而无需编写大量的 findViewById 和 setText/…...

【每日跟读】常用英语500句(200~300)
【每日跟读】常用英语500句 Home sweet home. 到家了 show it to me. 给我看看 Come on sit. 过来坐 That should do nicely. 这样就很好了 Get dressed now. 现在就穿衣服 If I were you. 我要是你 Close your eyes. 闭上眼睛 I don’t remember. 我忘了 I’m not su…...

【Java开发过程中的流程图】
流程图由一系列的图形符号和箭头组成,每个符号代表一个特定的操作或决策。下面是一些常见的流程图符号及其含义: 开始/结束符号(圆形):表示程序的开始和结束点。 过程/操作符号(矩形)ÿ…...

蓝桥杯刷题-day5-动态规划
文章目录 使用最小花费爬楼梯解码方法 使用最小花费爬楼梯 【题目描述】 给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。 你可以选择从下标为 0 或下标为 1 的台阶…...

新概念英语1:Lesson7内容详解
新概念英语1:Lesson7内容详解 如何询问人的个人信息 本课里有两个关于个人信息的问句,一个是问国籍,一个是问工作,句型如下: what nationality are you?询问国籍 回复一般就是我是哪国人,I’m Chinese…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...
