数据结构与算法-分治算法
数据结构与算法
数据结构与算法是计算机科学中的两个核心概念,它们在软件开发和问题解决中起着至关重要的作用。
数据结构
数据结构是计算机中存储、组织和管理数据的方式,它能够帮助我们高效地访问和修改数据。不同的数据结构适用于不同类型的应用场景。
常见的数据结构包括:
- 数组:一种线性数据结构,用于存储具有相同类型的元素集合,每个元素在内存中占据连续的位置。
- 链表:由节点组成的线性数据结构,每个节点包含数据和指向下一个节点的指针。
- 栈:一种后进先出(LIFO)的数据结构,常用于管理函数调用、表达式求值等。
- 队列:一种先进先出(FIFO)的数据结构,适用于任务调度、缓冲处理等场景。
- 树:一种分层数据结构,由节点组成,每个节点可以有零个或多个子节点。
- 图:由顶点(节点)和边组成,可以表示多对多的关系,适用于网络分析、路径查找等。
算法
算法是解决特定问题的一系列步骤和规则。算法的性能通常通过时间复杂度和空间复杂度来衡量。算法的设计和选择对程序的效率有很大影响。
常见的算法类型包括:
- 排序算法:如快速排序、归并排序、堆排序等,用于将数据集合按特定顺序排列。
- 搜索算法:如二分搜索、深度优先搜索(DFS)、广度优先搜索(BFS)等,用于在数据结构中查找特定元素。
- 图算法:如Dijkstra算法、A*搜索算法、Prim算法和Kruskal算法等,用于解决图中的最短路径、最小生成树等问题。
- 动态规划:一种通过将问题分解为重叠的子问题来解决问题的方法,适用于具有最优子结构特性的问题。
- 分治算法:将问题分解为若干个规模较小的子问题,递归解决子问题后合并结果,适用于某些特定类型的优化问题。
分治算法
分治算法是一种处理复杂问题的方法,它的核心思想是将一个大问题分解成若干个规模较小但类似于原问题的子问题,递归或迭代地解决这些子问题,然后将子问题的解合并以得到原问题的解。这种方法的关键在于“分”和“治”两个步骤:分是将问题分解,治是独立解决分解后的小问题。
分治算法通常适用于解决那些可以通过重复应用相同解决方案的问题,例如数组排序、矩阵乘法、快速幂计算等。
- 分治算法示意图
+-------------------+ +-------------------+ +-------------------+
| | | | | |
| 原问题(n个元素) | | 子问题1(n/2个元素) | | 子问题2(n/2个元素) |
| | | | | |
+-------------------+ +-------------------+ +-------------------+| | |v v v
+-------------------+ +-------------------+ +-------------------+
| | | | | |
| 子问题1继续分解 | | 子问题1继续分解 | | 子问题2继续分解 |
| (n/4个元素) | | (n/4个元素) | | (n/4个元素) |
| | | | | |
+-------------------+ +-------------------+ +-------------------+| | |v v v
+-------------------+ +-------------------+ +-------------------+
| | | | | |
| 最小子问题(1个元素) | | 最小子问题(1个元素) | | 最小子问题(1个元素) |
| | | | | |
+-------------------+ +-------------------+ +-------------------+| | |+------------+------------+ +------------+------------+合并操作 合并操作 合并操作
分治算法特点
- 分解:将原问题分解为若干个规模较小的相同类型的问题。
- 独立解决:递归或迭代地独立解决每个子问题。
- 合并:将子问题的解合并,形成原问题的解。
应用实例
- 归并排序(Merge Sort):一种分稳算法,将无序数组分为两半,递归地对两半进行排序,然后将排序好的两半合并成一个有序数组。
- 快速排序(Quick Sort):通过选定一个基准元素,将数组分为两部分,一部分包含所有小于基准的元素,另一部分包含所有大于基准的元素,然后递归地对这两部分进行快速排序。
- 快速幂算法(Fast Exponentiation):用于计算一个数的幂,通过将幂指数分解为若干个更小的幂指数,然后逐个计算并合并结果。
- 二分查找(Binary Search):在有序数组中查找特定元素,通过将数组分为两半并比较中间元素与目标值,逐步缩小搜索范围。
- Strassen矩阵乘法:一种矩阵乘法算法,通过分解和合并操作,减少了计算量,提高了计算效率。
注意事项
- 分治算法可能不适用于所有问题,需要确保问题可以被分解为独立的子问题,并且子问题的解可以容易地合并。
- 分治算法可能会引入额外的开销,如递归调用和数据复制,因此在某些情况下可能不是最优选择。
- 需要仔细设计分解和合并策略,以确保算法的效率和正确性。
分治算法c++示例
- 归并排序:归并排序的时间复杂度为 O(n log n),其中 n 是数组的大小。这种算法的优势在于其稳定性,即相等的元素在排序后保持原来的相对顺序。
#include <iostream>
#include <vector>// 合并两个有序数组
void merge(std::vector<int>& arr, int left, int mid, int right) {int n1 = mid - left + 1; // 左半部分的大小int n2 = right - mid; // 右半部分的大小// 创建临时数组std::vector<int> L(n1), R(n2);// 拷贝数据到临时数组for (int i = 0; i < n1; i++)L[i] = arr[left + i];for (int j = 0; j < n2; j++)R[j] = arr[mid + 1 + j];// 合并临时数组回原数组int i = 0, j = 0, k = left;while (i < n1 && j < n2) {if (L[i] <= R[j]) {arr[k] = L[i];i++;} else {arr[k] = R[j];j++;}k++;}// 拷贝剩余的左半部分元素while (i < n1) {arr[k] = L[i];i++;k++;}// 拷贝剩余的右半部分元素while (j < n2) {arr[k] = R[j];j++;k++;}
}// 归并排序的递归函数
void mergeSort(std::vector<int>& arr, int left, int right) {if (left < right) {// 找到中间位置int mid = left + (right - left) / 2;// 递归地对左右两部分进行排序mergeSort(arr, left, mid);mergeSort(arr, mid + 1, right);// 合并已排序的左右两部分merge(arr, left, mid, right);}
}// 打印数组的函数
void printArray(const std::vector<int>& arr) {for (int num : arr) {std::cout << num << " ";}std::cout << std::endl;
}// 主函数
int main() {std::vector<int> arr = {12, 11, 13, 5, 6, 7};std::cout << "Given array is \n";printArray(arr);mergeSort(arr, 0, arr.size() - 1);std::cout << "Sorted array is \n";printArray(arr);return 0;
}
- 二分查找:二分查找的时间复杂度为 O(log n),其中 n 是数组的大小。这种算法在处理大数据集时非常高效,尤其是在有序数据集上查找元素时。
#include <iostream>
#include <vector>// 二分查找函数
int binarySearch(const std::vector<int>& arr, int left, int right, int target) {while (left <= right) {// 计算中间位置的索引int mid = left + (right - left) / 2;// 如果找到目标值,返回索引if (arr[mid] == target) {return mid;}// 如果目标值小于中间元素,更新右边界else if (target < arr[mid]) {right = mid - 1;}// 如果目标值大于中间元素,更新左边界else {left = mid + 1;}}// 如果没有找到目标值,返回-1return -1;
}// 主函数
int main() {std::vector<int> arr = {2, 3, 4, 10, 40};int target = 10;// 调用二分查找函数int resultIndex = binarySearch(arr, 0, arr.size() - 1, target);// 输出结果if (resultIndex != -1) {std::cout << "Element found at index " << resultIndex << std::endl;} else {std::cout << "Element not found in the array." << std::endl;}return 0;
}
相关文章:

数据结构与算法-分治算法
数据结构与算法 数据结构与算法是计算机科学中的两个核心概念,它们在软件开发和问题解决中起着至关重要的作用。 数据结构 数据结构是计算机中存储、组织和管理数据的方式,它能够帮助我们高效地访问和修改数据。不同的数据结构适用于不同类型的应用场…...

MNN详细介绍、安装和编译
目录 第一章:MNN简介 1.1、MNN概述 1.2、MNN特点 1.3、MNN在移动端的应用优势 第二章:MNN安装与配置 2.1、环境准备 2.2、下载与编译 第三章:MNN使用指南 3.1、模型转换与部署 3.2、推理示例 第四章:MNN高级应用与优化技巧...
uniapp-Form示例(uviewPlus)
示例说明 Vue版本:vue3 组件:uviewPlus(Form 表单 | uview-plus 3.0 - 全面兼容nvue的uni-app生态框架 - uni-app UI框架) 说明:表单组建、表单验证、提交验证等; 截图: 示例代码 <templat…...
【Linux】详解进程程序替换
一、替换原理 用fork创建子进程后执行的是和父进程相同的程序(但有可能执行不同的代码分支),子进程往往要调用一种exec函数以执行另一个程序。当进程调用一种exec函数时,该进程的用户空间代码和数据完全被新程序替换,从新程序的启动例程开始执…...

vue中使用jsmind生成脑图
项目部分参数: vue:2.6.10 node:16.20.0 1、使用命令行安装jsmind: npm i jsmind -S 2、在文件中引入jsmind,并编写渲染jsmind的代码:: <template><!-- jsmind容器 --><divid"jsmi…...
yarn按包的时候报错 ../../../package.json: No license field
运行 yarn config list 然后运行 yarn config set strict-ssl false 之后yarn就成功了...
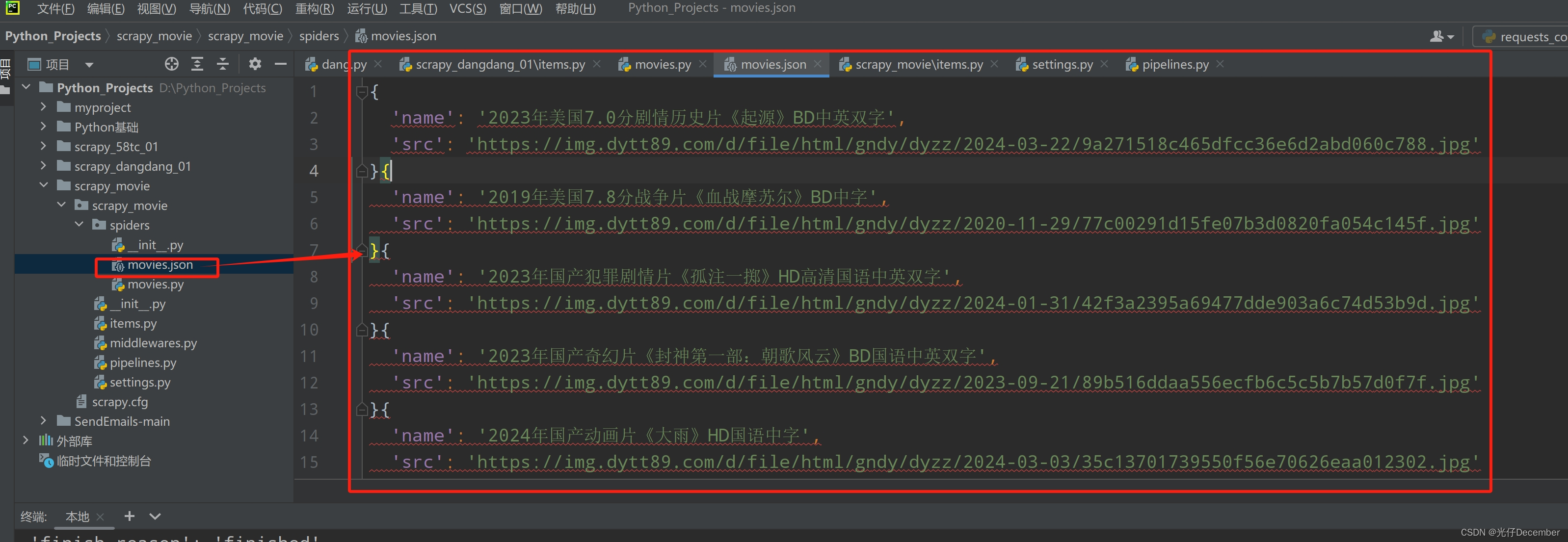
【Python从入门到进阶】51、电影天堂网站多页面下载实战
接上篇《50、当当网Scrapy项目实战(三)》 上一篇我们讲解了使用Scrapy框架在当当网抓取多页书籍数据的效果,本篇我们来抓取电影天堂网站的数据,同样采用Scrapy框架多页面下载的模式来实现。 一、抓取需求 打开电影天堂网站&…...
苹果CMS影视APP源码,二开版本带视频教程
编译app教程 工具下载:Android Studio 官网地址:https://developer.android.google.cn/studio/ 环境设置: 设置中文:https://blog.csdn.net/qq_37131111/article/details/131492844 汉化包找最新的下载就行了,随便下载…...

Zigbee技术在智能农业领域的应用研究
Zigbee技术在智能农业领域的应用研究 **摘要:**随着现代信息技术的飞速发展,智能农业已成为当今农业发展的新趋势。Zigbee技术作为一种低功耗、低成本的无线通信技术,在智能农业领域具有广泛的应用前景。本文深入分析了Zigbee技术的原理和特…...

Spring Cloud Gateway 中GET请求能正常访问,POST请求出现Unable to handle DataBuffer
报错信息如下: java.lang.IllegalArgumentException: Unable to handle DataBuffer of type class org.springframework.http.server.reactive.UndertowServerHttpRequest$UndertowDataBufferat org.springframework.cloud.gateway.filter.NettyRoutingFilter.getB…...

什么是git? 初步认识git 如何使用git
Git是什么? Git 是分布式版本控制系统,可以有效,高速地处理从很小到非常大地项目版本管理,分布式相比于集中式的最大区别在于开发者可以提交到本地,每个开发者可以通过克隆,在本地机器上拷贝一个完整的Git …...
Douyin视频详情数据API接口(视频详情,评论)
抖音官方并没有直接提供公开的视频详情数据采集API接口给普通用户或第三方开发者。抖音的数据采集通常受到严格的限制,以保护用户隐私和平台安全。 请求示例,API接口接入Anzexi58 如果您需要获取抖音视频详情数据,包括评论、点赞等ÿ…...
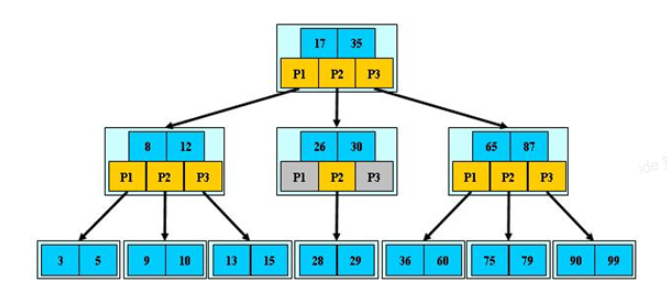
MySQL 索引:索引为什么使用 B+树?
Hash 索引不支持顺序和范围查询; 二叉查找树(BST):解决了排序的问题,极端情况下可能会退化成线性链表,查询效率急剧下降; 平衡二叉树(AVL) :通过旋转解决了平衡的问题,但是旋转操作效率太低&am…...

2024年第四届天府杯全国大学生数学建模竞赛B题思路
B题:新质生产力引领下的企业生产与发展策略优化 问题背景 随着技术的飞速发展,新质生产力如人工智能、大数据分析、物联网等技术被广泛应用于生产和服务过程中,极大地提高了生产效率和产品质量,改变了传统的生产与经营模式。一家…...

c++部分题
const关键字与宏定义的区别是什么? const关键字和宏定义在功能上有相似之处,但在实现和使用上有很大的区别。 作用域和类型安全性: const关键字定义的常量具有作用域和类型安全性。它们的作用域仅限于声明它们的块,并且在编译时会…...

验证回文串
如果在将所有大写字符转换为小写字符、并移除所有非字母数字字符之后,短语正着读和反着读都一样。则可以认为该短语是一个 回文串 。 字母和数字都属于字母数字字符。 给定一个字符串 s,如果它是 回文串 ,返回 true ;否则&#…...
vue2高德地图选点
<template><el-dialog :title"!dataForm.id ? 新建 : isDetail ? 详情 : 编辑" :close-on-click-modal"false" :visible.sync"show" class"rv-dialog rv-dialog_center" lock-scroll width"74%" :before-close&q…...

Gitflow:一种依据 Git 构建的分支管理工作流程模式
文章目录 前言Gitflow 背景Gitflow 中的分支模型Gitflow 的版本号管理简单模拟 Gitflow 工作流 前言 Gitflow 工作流是一种版本控制流程,主要适用于较大规模的团队。这个流程在团队中进行合作时可以避免冲突,并能快速地完成项目,因此在很多软…...

利用云手机技术,开拓海外社交市场
近年来,随着科技的不断进步,云手机技术逐渐在海外社交营销领域崭露头角。其灵活性、成本效益和全球性特征使其成为海外社交营销的利器。那么,究竟云手机在海外社交营销中扮演了怎样的角色呢? 首先,云手机技术能够消除地…...
脚本实现Ubuntu设置屏幕无人操作,自动黑屏
使用 xrandr 命令可以实现对屏幕的控制,包括调整分辨率、旋转屏幕以及关闭屏幕等。要实现 Ubuntu 设置屏幕在无人操作一段时间后自动黑屏,非待机,并黑屏后点击触摸屏可以唤醒屏幕,可以借助 xrandr 命令来实现。 首先,…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

Android写一个捕获全局异常的工具类
项目开发和实际运行过程中难免会遇到异常发生,系统提供了一个可以捕获全局异常的工具Uncaughtexceptionhandler,它是Thread的子类(就是package java.lang;里线程的Thread)。本文将利用它将设备信息、报错信息以及错误的发生时间都…...
