VMware虚拟机更换引导顺序
前言
我用wmware装了黑群晖测试,将img转成vmdisk的格式之后发现系统引导盘之后1G,有点太小了
我准备把wmware的黑群晖系统迁移到新添加的虚拟磁盘里
1.登录黑群晖的SSH
请先在黑群晖的控制面板中的终端机和SNMP里面启用SSH功能,才能使用ssh链接
2.使用dd命令克隆系统
superchen@nas:~$ sudo dd if=/dev/synoboot of=/dev/sdg bs=1M status=progress
998244352 bytes (998 MB, 952 MiB) copied, 8 s, 125 MB/s
1024+0 records in
1024+0 records out
1073741824 bytes (1.1 GB, 1.0 GiB) copied, 8.83912 s, 121 MB/s
3.修改vmware虚拟机启动引导
打开电源时进入固件
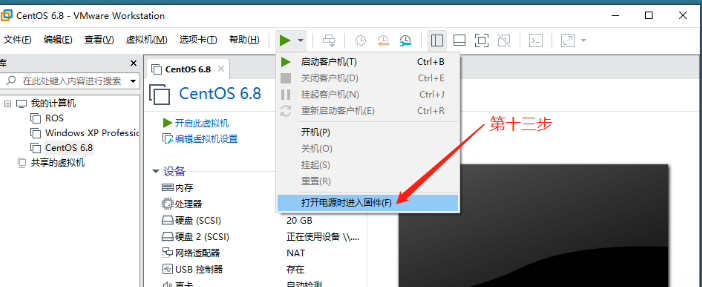
进入固件blos之后,键盘 -> 移动到Boot选项
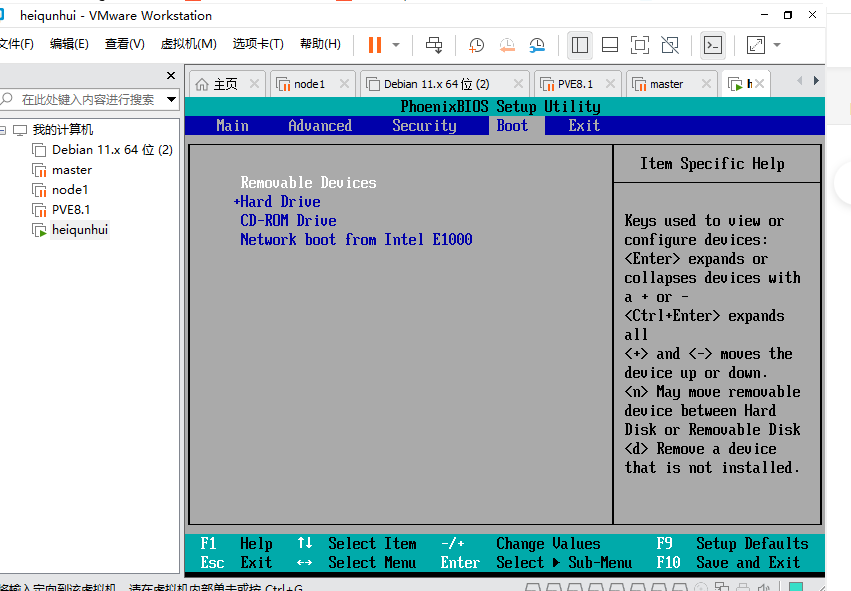
选择Hard Drive然后回车
将我们要引导的盘设置成第一(使用键盘的+ 或者 - 键调整顺序)

将这个2:4:0:6 看最后的数字代表了第6个盘
具体可以看虚拟机的硬盘设置
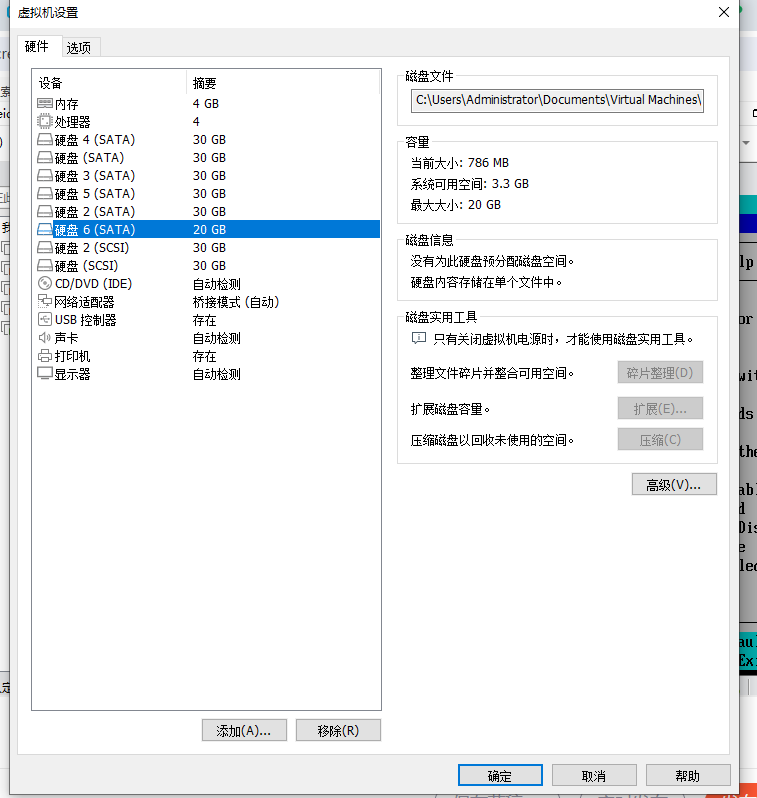
这个20G的虚拟磁盘就是我们刚才将系统克隆到的盘,显示硬盘6
然后F10保存设置,跳出来一个弹框选择yes,就会重启进入引导系统
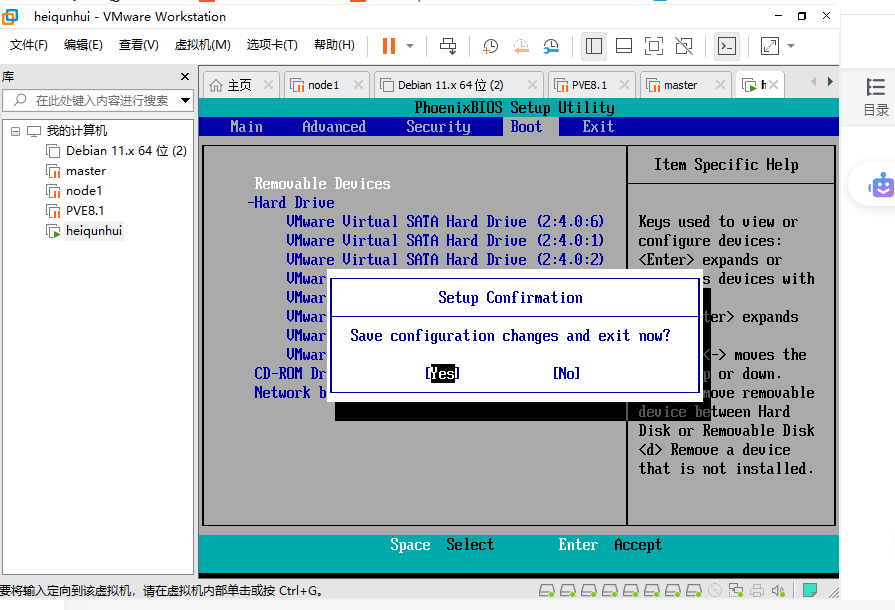
相关文章:

VMware虚拟机更换引导顺序
前言 我用wmware装了黑群晖测试,将img转成vmdisk的格式之后发现系统引导盘之后1G,有点太小了 我准备把wmware的黑群晖系统迁移到新添加的虚拟磁盘里 1.登录黑群晖的SSH 请先在黑群晖的控制面板中的终端机和SNMP里面启用SSH功能,才能使用ss…...
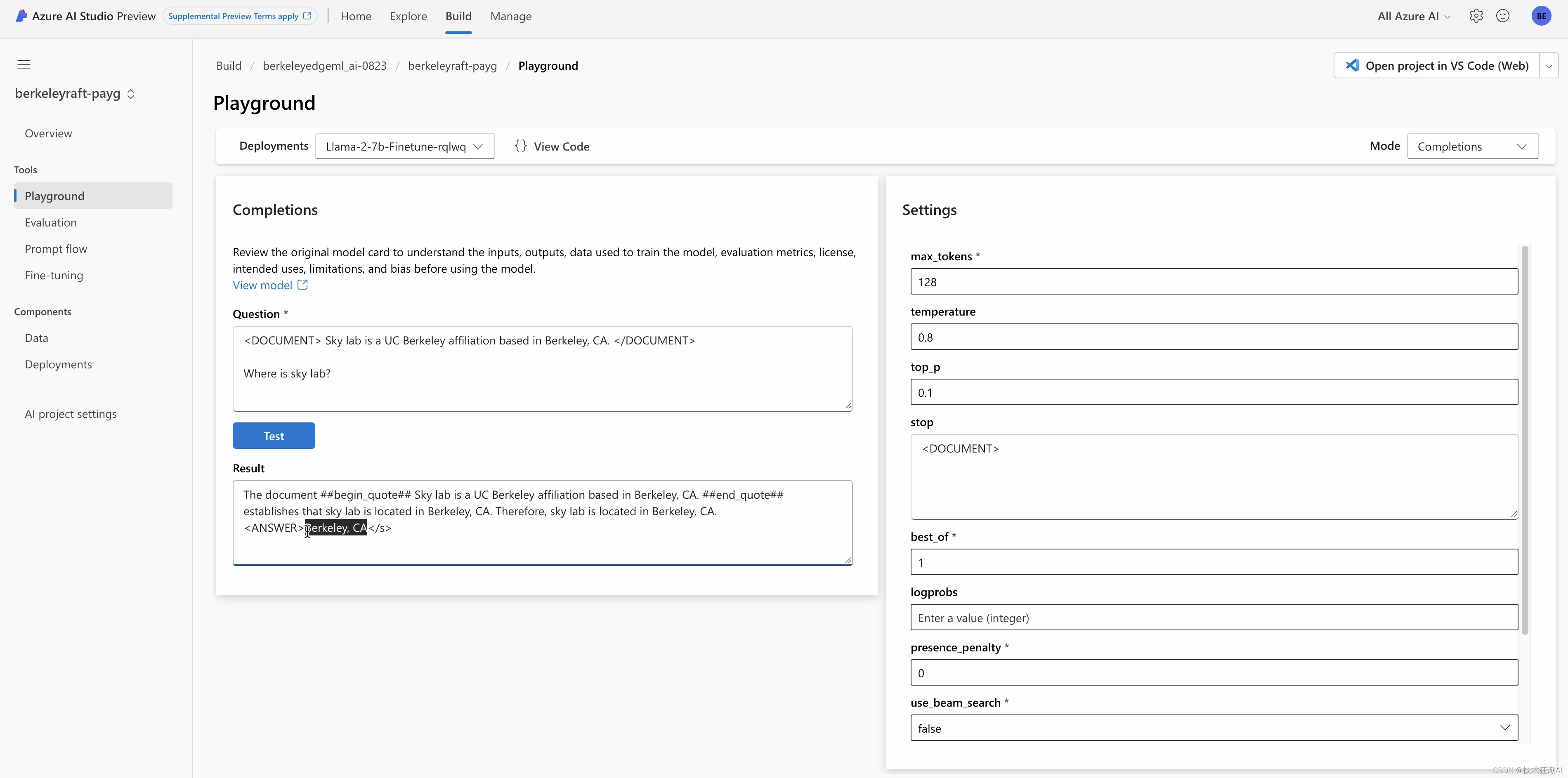
RAFT:让大型语言模型更擅长特定领域的 RAG 任务
RAFT(检索增强的微调)代表了一种全新的训练大语言模型(LLMs)以提升其在检索增强生成(RAG)任务上表现的方法。“检索增强的微调”技术融合了检索增强生成和微调的优点,目标是更好地适应各个特定领…...

Stable Diffusion 本地训练端口与云端训练端口冲突解决办法
方法之一,修改本地训练所用的端口 1 首先,进入脚本训练器的根目录 例如:C:\MarkDeng\lora-scripts-v1.7.3 找到gui.py 2 修改端口号 因为云端训练器也是占用28000和6006端口 那么本地改成27999和6007也是可以的 保存退出,运行启动…...

C++学习day1
思维导图 定义自己的命名空间,其中有string类型的变量,再定义两个函数,一个函数完成字符串的输入,一个函数完成求字符串长度,再定义一个全局函数完成对该字符串的反转 #include <iostream> using namespace std;…...

openGauss CM
CM 可获得性 本特性自openGauss 3.0.0版本开始引入。 特性简介 CM(Cluster Manager)是一款数据库管理软件,由cm_server和cm_agent组成。 cm_agent是部署在数据库每个主机上,用来启停和监控各个数据库实例进程的数据库管理组件…...
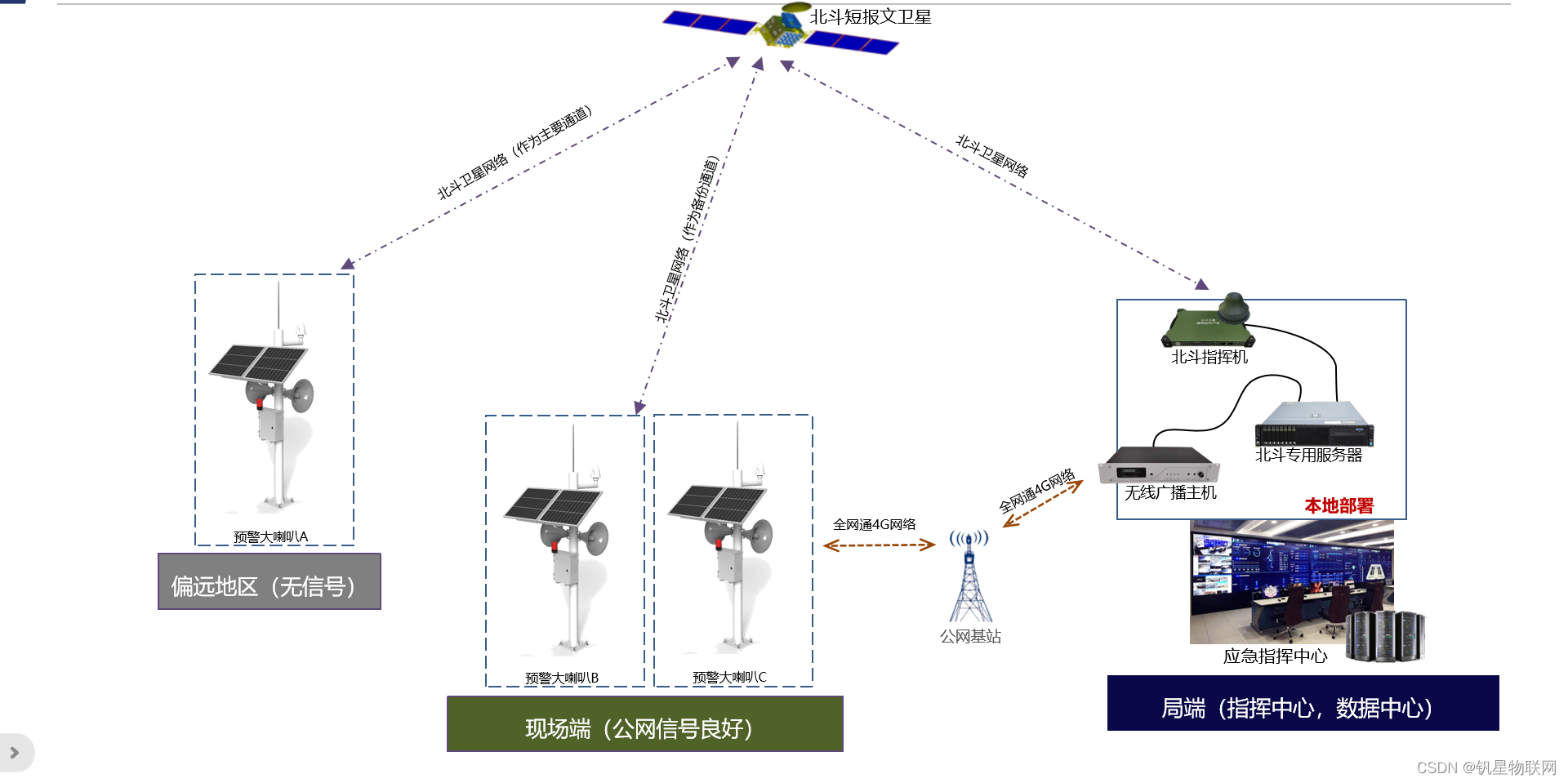
北斗短报文+4G应急广播系统:实时监控 自动预警 保护校园安全的新力量
安全无小事,生命重如山。学生是祖国的未来,校园安全是全社会安全工作的一个重要的组成部分。它直接关系到青少年学生能否安健康地成长,关系到千千万万个家庭的幸福安宁和社会稳定。 灾害事故和突发事件频频发生,给学生、教职员工…...

2024河北石家庄矿业矿山展览会|河北智慧矿山展会|河北矿博会
2024中国(石家庄)国际矿业博览会 时间:2024年7月4-6日 地点:石家庄国际会展中心.正定 随着全球经济的持续增长和矿产资源需求的不断攀升,矿业行业正迎来前所未有的发展机遇。作为矿业领域的盛会&…...

ruoyi使用笔记
1.限流处理 RateLimiter PostMapping("/createOrder") ApiOperation("创建充值订单") RateLimiter(key CacheConstants.REPEAT_SUBMIT_KEY,time 10,count 1,limitType LimitType.IP) public R createOrder(RequestBody Form form) {//业务处理return …...

论文《Exploring to Prompt for Vision-Language Models》阅读
论文《Exploring to Prompt for Vision-Language Models》阅读 论文概况论文动机(Intro)MethodologyPreliminaryCoOp[CLASS]位置Context 是否跨 class 共享表示和训练 ExperimentsOverall ComparisonDomain GeneralizationContext Length (M) 和 backbon…...

科普 | Runes 预挖矿概念
作者:Jacky X/推:zxl2102492 关于 Runes 协议的前世今生,可以点击阅读这篇文章 👇 《简述 Runes 协议、发展历程及最新的「公开铭刻」发行机制的拓展讨论》 什么是传统预挖矿概念 这轮比特币生态爆发之前,预挖矿&…...
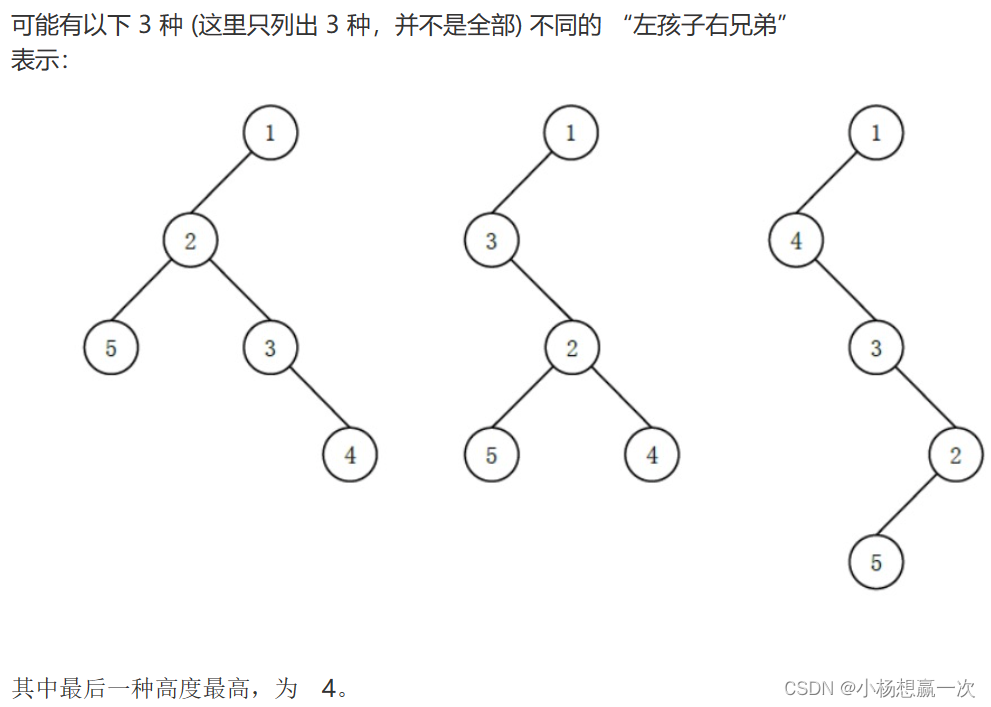
蓝桥杯真题Day40 倒计时19天 纯练题!
蓝桥杯第十三届省赛真题-统计子矩阵 题目描述 给定一个 N M 的矩阵 A,请你统计有多少个子矩阵 (最小 1 1,最大 N M) 满足子矩阵中所有数的和不超过给定的整数 K? 输入格式 第一行包含三个整数 N, M 和 K. 之后 N 行每行包含 M 个整数…...

Android 14.0 SystemUI下拉状态栏增加响铃功能
1.概述 在14.0的系统产品rom定制化开发中,在对systemui的状态栏开发中,对SystemUI下拉状态栏的QuickQSPanel区域有快捷功能键开关,对于增加各种响铃快捷也是常用功能, 有需要增加响铃功能开关功能,接下来就来分析SystemUI下拉状态栏QuickQSPanel快捷功能键开关的相关源码…...

docker学习笔记 二-----docker介绍
老套路哈,第一章先科普一下三种常见的云服务类型,第二和第三章节写docker学习笔记。 一 、IAAS、PAAS、SAAS IAAS (Infrastructure as a Service):基础即服务,供应商仅提供给用户最基础设施的服务资源,也就是服务器资…...
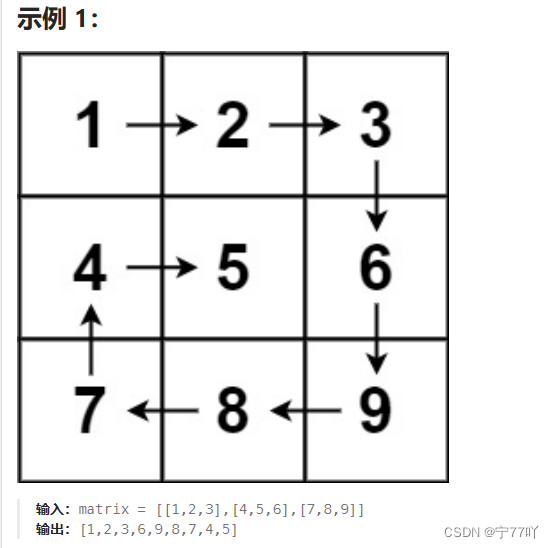
螺旋矩阵的算法刷题
螺旋矩阵的算法刷题 本文主要涉及螺旋矩阵的算法 包括三个题目分别是 59. 螺旋矩阵 II54. 螺旋矩阵 中等LCR 146. 螺旋遍历二维数组 文章目录 螺旋矩阵的算法刷题一 、螺旋矩阵简单1.1 实现一(我认为这个方法更巧妙!!)1.2 实现二&…...
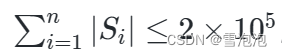
蓝桥杯算法赛(二进制王国)
问题描述 二进制王国是一个非常特殊的国家,因为该国家的居民仅由 0 和 1 组成。 在这个国家中,每个家庭都可以用一个由 0 和 1 组成的字符串 S 来表示,例如 101、 000、 111 等。 现在,国王选了出 N 户家庭参加邻国的庆典…...
7.JDK下载和安装
文章目录 一、下载二、安装三、JDK的安装目录介绍 写JAVA代码不是随随便便能写的,我们得先做一点准备工作。例如,我们平时想要玩一把游戏,就需要先下载、安装才能玩游戏。JAVA也是一样的,也是需要下载并安装相关的软件,…...

Java序列化之Jackson详解
文章目录 1 Jackson1.1 Jackson简介1.2 为什么选择Jackson1.3 Jackson的基本功能1.3.1 将Java对象转换为JSON字符串(序列化)1.3.2 将JSON字符串转换为Java对象(反序列化) 1.4 Jackson库主要方法1.5 使用Jackson基本步骤1.5.1 添加…...

深入Facebook的世界:探索数字化社交的无限可能性
引言 随着数字化时代的到来,社交媒体平台已经成为了人们日常生活中不可或缺的一部分,而其中最为突出的代表之一便是Facebook。作为全球最大的社交媒体平台之一,Facebook不仅仅是一个社交网络,更是一个数字化社交的生态系统&#…...

HTML 怎么解决上下标问题呢?
当我们阅读内容时,经常会遇到特殊格式的文本,如化学式的下标和数学公式的上标,sub 标签和sup 标签就是用来解决这个问题的。 1. 基础语法 什么是 sub 和sup标签 sub 标签用于定义下标文本,而 sup 标签用于定义上标文本。 这些…...

题目 2880: 计算鞍点
题目描述: 给定一个5*5的矩阵,每行只有一个最大值,每列只有一个最小值,寻找这个矩阵的鞍点。 鞍点指的是矩阵中的一个元素,它是所在行的最大值,并且是所在列的最小值。 例如:在下面的例子中(第…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...
