螺旋矩阵的算法刷题

螺旋矩阵的算法刷题

本文主要涉及螺旋矩阵的算法
包括三个题目分别是

1. 59. 螺旋矩阵 II
2. 54. 螺旋矩阵 中等
3. LCR 146. 螺旋遍历二维数组

一 、螺旋矩阵简单

59. 螺旋矩阵 II

给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix .

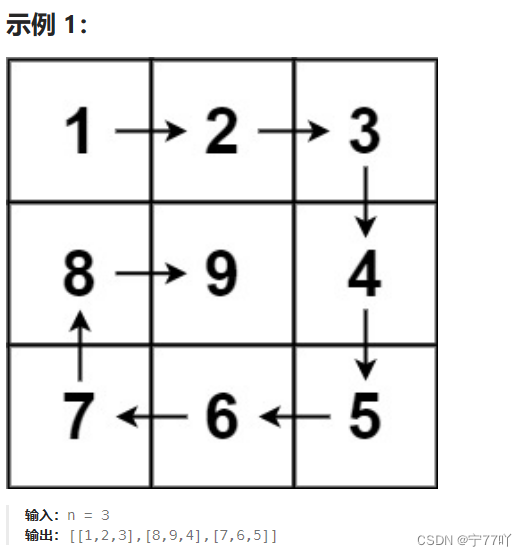
1.1 实现一（我认为这个方法更巧妙！！）

思路：
采用了类似螺旋走位的方式进行填充，具体实现如下：

1. 首先，定义一个n x n的二维数组res来存储结果。
2. 初始化方向向量dx和dy，初始值分别为0和1，表示向右移动。
3. 初始化坐标x和y，初始值都为0，表示从矩阵的左上角开始填充。
4. 使用一个循环，从1到n * n遍历每个要填充的数字。
5. 在每一步中，将当前位置的值设置为当前遍历的数字i，并根据当前方向向量(dx, dy)进行移动到下一个位置。
6. 判断下一个位置是否已经被填充过，如果是，则表示已经到达边界，需要调转方向向量以继续填充；如果不是，则继续沿当前方向向量移动。
7. 返回填充完成的二维数组res作为结果。

这样的算法可以确保填充的数字形成了一个螺旋状的矩阵。

C++代码实现

class Solution {
public:vector<vector<int>> generateMatrix(int n) {vector<vector<int>> matrix(n,vector<int>(n,0));//代表方向的向量变量 01--右 10--下 -1 0--左 0 -1 --上int dx=0,dy=1;//x,y表示当前坐标int x=0,y=0;//使用for进行循环，i表示当前值for(int i =1; i<=n*n;i++){matrix[x][y]=i;//**关键部分**if(matrix[(x+dx+n)%n][(y+dy+n)%n]!=0)//判断是否已经填充，如果已经填充则向量需要换方向{int temp = dy;dy=-dx;dx=temp;}x+=dx;y+=dy;}return matrix;    }
};

重要的是下面这段代码

 if(matrix[(x+dx+n)%n][(y+dy+n)%n]!=0)//判断是否已经填充，如果已经填充则向量需要换方向{int temp = dy;dy=-dx;dx=temp;}

这段代码是在判断当前位置的下一个位置是否已经被填充过。如果下一个位置已经被填充过，说明当前位置已经是当前层的最后一个位置，需要改变填充方向。

逐行解释这段代码：

1. (x + dx + n) % n：这里计算了下一个位置的横坐标。由于是螺旋填充，因此下一个位置可能超出边界。使用 % n 可以将超出边界的情况转化为在边界内的情况。例如，当 x + dx 大于等于 n 时，超出了右边界，通过 % n 可以将其映射到左边界，从而形成循环填充。
2. 同理，(y + dy + n) % n 计算了下一个位置的纵坐标。
3. res[(x + dx + n) % n][(y + dy + n) % n] != 0：这个条件判断当前位置的下一个位置是否已经被填充过。如果下一个位置不等于0，说明已经被填充过。
4. 如果下一个位置已经被填充过，则需要改变填充方向。通过交换 dx 和 dy 实现了向下转向的功能。
5. int tem = dy; dy = -dx; dx = tem;：这里使用了一个临时变量 tem，先将 dy 的值保存下来，然后将 dy 设置为 -dx，dx 设置为 tem，实现了方向的转换。

总的来说，这段代码的作用是在当前位置的下一个位置已经被填充过时，改变填充方向，从而继续填充螺旋矩阵。

1.2 实现二（经典方法–更加直观）

一个常见的方法是按层次遍历，逐层填充螺旋矩阵。具体步骤如下：

1. 初始化一个n x n的二维数组res，用于存储结果。
2. 定义四个变量top、bottom、left、right，分别表示当前填充层的上下左右边界。
3. 初始化这些边界值：top=0，bottom=n-1，left=0，right=n-1。
4. 初始化一个变量num，表示当前要填充的数字，初始值为1。
5. 在一个循环中，依次填充每一层的数字，直到所有位置都被填充为止。
   • 从左到右，将当前层的最上一行从left到right填充为num开始递增的数字，同时更新top的值使其向下移动一行。
   • 从上到下，将当前层的最右一列从top到bottom填充为num开始递增的数字，同时更新right的值使其向左移动一列。
   • 从右到左，将当前层的最下一行从right到left填充为num开始递增的数字，同时更新bottom的值使其向上移动一行。
   • 从下到上，将当前层的最左一列从bottom到top填充为num开始递增的数字，同时更新left的值使其向右移动一列。
   • 每填充完一行或一列后，将num递增。
6. 当top > bottom 或 left > right时，表示所有位置都被填充完毕，退出循环。
7. 返回填充完成的二维数组res作为结果。

这样的实现方法更直观清晰，容易理解和实现，并且效率也很高。

class Solution {
public:vector<vector<int>> generateMatrix(int n) {vector<vector<int>> res(n, vector<int>(n, 0)); // 初始化结果矩阵为全零int top = 0, bottom = n - 1, left = 0, right = n - 1; // 初始化边界int num = 1; // 当前要填充的数字，初始为1while (true) {// 从左到右，填充最上一行for (int i = left; i <= right; ++i) {res[top][i] = num++;}if (++top > bottom) break; // 更新上边界，若超过下边界则退出// 从上到下，填充最右一列for (int i = top; i <= bottom; ++i) {res[i][right] = num++;}if (--right < left) break; // 更新右边界，若超过左边界则退出// 从右到左，填充最下一行for (int i = right; i >= left; --i) {res[bottom][i] = num++;}if (--bottom < top) break; // 更新下边界，若超过上边界则退出// 从下到上，填充最左一列for (int i = bottom; i >= top; --i) {res[i][left] = num++;}if (++left > right) break; // 更新左边界，若超过右边界则退出}return res;}
};

二、螺旋矩阵 中等

54. 螺旋矩阵 中等

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

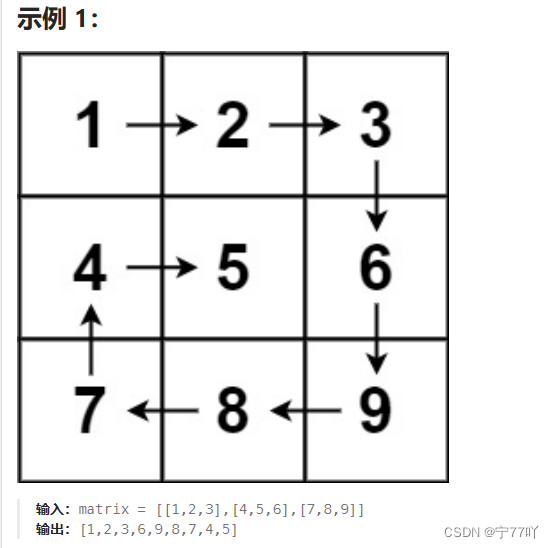
2.1 实现一（经典）

class Solution {
public:vector<int> spiralOrder(vector<vector<int>>& matrix) {vector<int> ans;if (matrix.empty()) return ans;int m = matrix.size(); // 行数int n = matrix[0].size(); // 列数int top = 0, bottom = m - 1, left = 0, right = n - 1;while (top <= bottom && left <= right) {// 从左到右遍历上边界for (int j = left; j <= right; ++j) {ans.push_back(matrix[top][j]);}++top;// 从上到下遍历右边界for (int i = top; i <= bottom; ++i) {ans.push_back(matrix[i][right]);}--right;// 从右到左遍历下边界if (top <= bottom) { // 防止重复访问上一次遍历的元素for (int j = right; j >= left; --j) {ans.push_back(matrix[bottom][j]);}--bottom;}// 从下到上遍历左边界if (left <= right) { // 防止重复访问上一次遍历的元素for (int i = bottom; i >= top; --i) {ans.push_back(matrix[i][left]);}++left;}}return ans;}
};

按照螺旋顺序遍历二维矩阵。下面是对代码的详细解释：

1. 首先，定义一个空的整数向量 ans 用于存储遍历结果。
2. 如果输入的二维矩阵 matrix 为空，直接返回空的结果向量 ans。
3. 获取矩阵的行数 m 和列数 n，以及初始化四个边界变量 top、bottom、left 和 right。
4. 在一个循环中，不断遍历矩阵的边界元素，直到边界收缩到无效为止。
   • 从左到右遍历上边界，将上边界的元素依次加入结果向量 ans 中，并将 top 上移一行。
   • 从上到下遍历右边界，将右边界的元素依次加入结果向量 ans 中，并将 right 右移一列。
   • 从右到左遍历下边界，将下边界的元素依次加入结果向量 ans 中，并将 bottom 下移一行（注意要判断 top <= bottom，防止重复遍历）。
   • 从下到上遍历左边界，将左边界的元素依次加入结果向量 ans 中，并将 left 左移一列（注意要判断 left <= right，防止重复遍历）。
5. 循环结束后，返回结果向量 ans。

利用边界变量控制了螺旋顺序的遍历过程，实现了按照螺旋顺序遍历二维矩阵的功能。

2.2 实现二（精妙！！）

下面是一段Python代码:

def spiralOrder(self, matrix: List[List[int]]) -> List[int]:res = []while matrix:# 削头（第一层）res += matrix.pop(0)# 将剩下的逆时针转九十度，等待下次被削matrix = list(zip(*matrix))[::-1]return res

采用了不断“削头”的方式来实现。具体的步骤如下：

1. 创建一个空列表 res 用于存储螺旋顺序遍历的结果。
2. 使用 while matrix: 循环来遍历矩阵，直到矩阵为空。
3. 在每一次循环中，先将矩阵的第一行（即第一层）添加到结果列表 res 中，然后将该行从矩阵中移除。
4. 接着，将剩下的矩阵逆时针旋转 90 度（将其转置后再沿着竖直方向反转），以便下次循环时能够继续削头。
5. 重复上述步骤直到矩阵为空。

这种方法的思路简洁，通过不断调整矩阵的结构来实现螺旋顺序遍历，避免了显式的控制遍历方向和边界条件的处理。

在实际代码中，matrix.pop(0) 用于削头，list(zip(*matrix))[::-1] 用于逆时针旋转矩阵。

如果是C++实现类似削头的效果：

#include <vector>class Solution {
public:vector<int> spiralOrder(vector<vector<int>>& matrix) {vector<int> res;while (!matrix.empty()) {// 削头（第一层）for (auto it = matrix[0].begin(); it != matrix[0].end(); ++it) {res.push_back(*it);}matrix.erase(matrix.begin()); // 删除第一行// 将剩下的逆时针转九十度，等待下次被削if (!matrix.empty()) {vector<vector<int>> new_matrix;for (int j = matrix[0].size() - 1; j >= 0; --j) {vector<int> column;for (int i = 0; i < matrix.size(); ++i) {column.push_back(matrix[i][j]);}new_matrix.push_back(column);}matrix = new_matrix;}}return res;}
};

三、螺旋遍历矩阵 简单

LCR 146. 螺旋遍历二维数组

上面这个题是企业题，同类型的题目可以多练习练习~