牛客周赛 Round 38
牛客竞赛_ACM/NOI/CSP/CCPC/ICPC算法编程高难度练习赛_牛客竞赛OJ (nowcoder.com)
A-小红的正整数自增_牛客周赛 Round 38 (nowcoder.com)
取出最后一位判断即可
#include<iostream>
#include<algorithm>
#include<vector>
#include<set>
#include<queue>
#include<map>
#include<string>
#include<cmath>
#include<bitset>
#include<sstream>//切割strtream头文件
#include<climits>//INT_MAX文件
#include <utility>
using i64 = int64_t;
using namespace std;
#define int i64
#define endl '\n'
#define AC return 0;
#define WA cout << "SHU_YUAN" << endl;
const int maxn = 1e6 + 10;
int n, m, k, d, T = 1, A, B;void solve()
{string s;cin >> s;char ch = s.back();int x = (ch ^ 48);x = 10 - x;cout << (x == 10 ? 0 : x);
}signed main() {cin.tie(0) -> sync_with_stdio(false);int T = 1;//cin >> T;while (T--) solve();return 0;
}
B-小红的抛弃后缀_牛客周赛 Round 38 (nowcoder.com)
小红拿到了一个正整数,她准备切掉一个后缀并抛弃,使得剩余部分是9的倍数。小红想知道有多少种不同的操作方案?
因为删除的后缀是连续的,即有多少前缀满足是9的倍数,从前往后O(n)判断即可
#include<iostream>
#include<algorithm>
#include<vector>
#include<set>
#include<queue>
#include<map>
#include<string>
#include<cmath>
#include<bitset>
#include<sstream>//切割strtream头文件
#include<climits>//INT_MAX文件
#include <utility>
using i64 = int64_t;
using namespace std;
#define int i64
#define endl '\n'
#define AC return 0;
#define WA cout << "SHU_YUAN" << endl;
const int maxn = 1e6 + 10;
int n, m, k, d, T = 1, A, B;void solve()
{string s;cin >> s;int sum = 0;int ans = 0;for(auto &x : s){sum = sum * 10 + (x ^ 48);if(sum % 9 == 0)ans += 1;sum %= 9;}cout << ans;
}signed main() {cin.tie(0) -> sync_with_stdio(false);int T = 1;//cin >> T;while (T--) solve();return 0;
}C-小红的字符串构造_牛客周赛 Round 38 (nowcoder.com)
小红希望你构造一个长度为nnn的、仅包含小写字母的字符串,其中恰好有kkk个长度大于1的回文子串。你能帮帮她吗
有2种方式:因为k <= n / 2
所以可以通过前k个由2个相同字符(a -> z轮流输出),后 n - 2k个乱序即可
我的方式是先用前几个字符找到可达到的最大值,挨个靠近,最后的剩下的乱序,这样k可以不局限于k <= n / 2,k可以取n个字符能达到的最多回文数
// Problem: 小红的字符串构造
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/contest/78292/C
// Memory Limit: 524288 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)#include<iostream>
#include<algorithm>
#include<vector>
#include<set>
#include<queue>
#include<map>
#include<string>
#include<cmath>
#include<bitset>
#include<sstream>//切割strtream头文件
#include<climits>//INT_MAX文件
#include <utility>
using i64 = int64_t;
using namespace std;
#define int i64
#define endl '\n'
#define AC return 0;
#define WA cout << "SHU_YUAN" << endl;
const int maxn = 1e6 + 10;
int n, m, k, d, T = 1, A, B;
/*
aa 1
aaa 3
aaaa 6
aaaaa 10
*/
string s = "qwertyuiopasdfghjklzxcvbnm";
void solve()
{cin >> n >> k;int pos = 0;int t = 0;while(k){k--; t+=2;cout << s[pos] << s[pos];int cnt = 2;while(k >= cnt){cout << s[pos];k -= cnt;cnt++;t++;}pos = (pos + 1) % 26;}//cout <<"T = " << t << endl;for(int i = 1; i <= n - t;i++){cout << (s[(pos + i) % 26]);}
}signed main() {cin.tie(0) -> sync_with_stdio(false);int T = 1;//cin >> T;while (T--) solve();return 0;
}D-小红的平滑值插值_牛客周赛 Round 38 (nowcoder.com)
显然该题最终只有3个情况
情况1:最大平滑值 == k,无需操作
情况2:最大平滑值 < k,可证明最多只需一次操作,随便列一组数据即可:如k取7
最大平滑值取 任意x < 7,即任意1 < =i < j <= n abs(a[j] - a[i])< 7
1 7 ==> 在1后面插入一个 8 即可
1 3 == > 依旧插入一个8即可
显而易见若最大平滑值abs(a[x] - a[y] ) < k == > 在a[x] a[y]中间插入a[x] + k即可
情况3:最大平滑值 > k
在每一个平滑值大于k的数中间插入一个大小为x,首项为a[X] + k,d = k的等差数列,其中x = a[y] /a[x]向下取整
特例若可以整除需要减1 ,原因最后一项大小 == a[y]因此无需插入
// Problem: 小红的平滑值插值
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/contest/78292/D
// Memory Limit: 524288 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)#include<iostream>
#include<algorithm>
#include<vector>
#include<set>
#include<queue>
#include<map>
#include<string>
#include<cmath>
#include<bitset>
#include<sstream>//切割strtream头文件
#include<climits>//INT_MAX文件
#include <utility>
using i64 = int64_t;
using namespace std;
#define int i64
#define endl '\n'
#define AC return 0;
#define WA cout << "SHU_YUAN" << endl;
const int maxn = 1e6 + 10;
int n, m, k, d, T = 1, A, B;
int a[maxn];
int pos = 0;
int fun(int a, int b)
{return a % b == 0 ? a / b - 1 :a / b;
}void solve()
{cin >> n >> k;for(int i = 1;i <= n;i++)cin >> a[i];int mk = 0;int ans = 0;for(int i = 2;i <= n;i++){int t = abs(a[i] - a[i - 1]);if(t > k){ans += fun(t, k);}mk = max(mk, t);}if(mk == k)cout << 0;else if(mk > k)cout << ans; else cout << 1;}signed main() {cin.tie(0) -> sync_with_stdio(false);int T = 1;//cin >> T;while (T--) solve();return 0;
}E-小苯的等比数列_牛客周赛 Round 38 (nowcoder.com)
暴力枚举即可
// Problem: 小苯的等比数列
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/contest/78292/E
// Memory Limit: 524288 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)#include<iostream>
#include<algorithm>
#include<vector>
#include<set>
#include<queue>
#include<map>
#include<string>
#include<cmath>
#include<bitset>
#include<sstream>//切割strtream头文件
#include<climits>//INT_MAX文件
#include <utility>
using i64 = int64_t;
using namespace std;
#define int i64
#define endl '\n'
#define AC return 0;
//#define for(a -> b) for(int i = a; i <= b;i++)
#define WA cout << "SHU_YUAN" << endl;
const int maxn = 1e6 + 10;
int n, m, k, d, T = 1, A, B;
vector<int>v;
int M[maxn];
int cnt[maxn];void solve()
{cin >> n;int ans = 0;for(int i = 1;i <= n;i++){cin >> m;M[m] += 1;ans = max(ans, M[m]);}for(int i = 1; i <= 2e5; i++){if(M[i])for(int j = 2; i * j <= 2e5; j++){int cnt = 1;if(M[i * j]){for(int k = i * j; k <= 2e5; k *= j){if(M[k])ans = max(ans, ++cnt);else break;}}}}cout << ans << endl;
}signed main() {cin.tie(0) -> sync_with_stdio(false);int T = 1;//cin >> T;while (T--) solve();return 0;
}F-小苯的回文询问_牛客周赛 Round 38 (nowcoder.com)
因为是不连续的,因此每一次对于M[a[i]]的更新即是最后一次出现a[i]的位置
我们只需要找到最近可满足的坐标
当查找区间l r时,我们通过找到r位置最近可以形成回文的位置,若其大于等于l说明该区间有子区间满足不连续的回文串,其中如果dp[r] = 0说明没有回文串可形成
// Problem: 小苯的回文询问
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/contest/78292/F
// Memory Limit: 524288 MB
// Time Limit: 4000 ms
//
// Powered by CP Editor (https://cpeditor.org)#include<iostream>
#include<algorithm>
#include<vector>
#include<set>
#include<queue>
#include<map>
#include<string>
#include<cmath>
#include<bitset>
#include<sstream>//切割strtream头文件
#include<climits>//INT_MAX文件
#include <utility>
using i64 = int64_t;
using namespace std;
#define int i64
#define endl '\n'
#define AC return 0;
#define WA cout << "SHU_YUAN" << endl;
const int maxn = 1e6 + 10;
int n, m, k, d, q, T = 1, A, B;
int a[maxn],dp[maxn];//第i位往前最近可构成回文的坐标
map<int,int>M;
void solve()
{cin >> n >> q;for(int i = 1;i <= n;i++)cin >> a[i];for(int i = 1;i <= n;i++){dp[i] = max(dp[i - 1], M[a[i]]);if(i - 1)M[a[i - 1]] = i - 1;}while(q--){int l, r;cin >> l >> r;cout << (dp[r] >= l ? "YES" : "NO") << endl;}
}signed main() {cin.tie(0) -> sync_with_stdio(false);int T = 1;//cin >> T;while (T--) solve();return 0;
}
相关文章:

牛客周赛 Round 38
牛客竞赛_ACM/NOI/CSP/CCPC/ICPC算法编程高难度练习赛_牛客竞赛OJ (nowcoder.com) A-小红的正整数自增_牛客周赛 Round 38 (nowcoder.com) 取出最后一位判断即可 #include<iostream> #include<algorithm> #include<vector> #include<set> #include…...

漏洞扫描操作系统识别技术原理
漏洞扫描过程中,操作系统识别技术是至关重要的一步,因为它有助于扫描器针对性地选择适用的漏洞检测规则,提高扫描的准确性和效率。以下是漏洞扫描中操作系统识别技术的主要原理: **1. **TCP/IP 协议栈指纹识别** **原理**&#…...

数据结构与算法-分治算法
数据结构与算法 数据结构与算法是计算机科学中的两个核心概念,它们在软件开发和问题解决中起着至关重要的作用。 数据结构 数据结构是计算机中存储、组织和管理数据的方式,它能够帮助我们高效地访问和修改数据。不同的数据结构适用于不同类型的应用场…...

MNN详细介绍、安装和编译
目录 第一章:MNN简介 1.1、MNN概述 1.2、MNN特点 1.3、MNN在移动端的应用优势 第二章:MNN安装与配置 2.1、环境准备 2.2、下载与编译 第三章:MNN使用指南 3.1、模型转换与部署 3.2、推理示例 第四章:MNN高级应用与优化技巧...
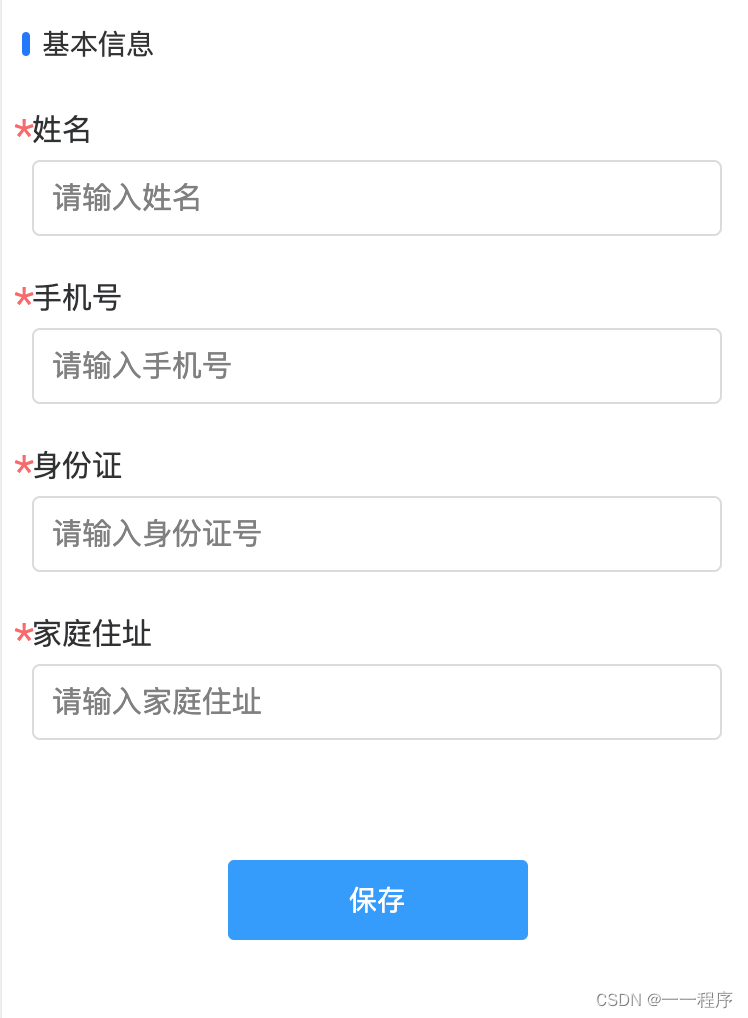
uniapp-Form示例(uviewPlus)
示例说明 Vue版本:vue3 组件:uviewPlus(Form 表单 | uview-plus 3.0 - 全面兼容nvue的uni-app生态框架 - uni-app UI框架) 说明:表单组建、表单验证、提交验证等; 截图: 示例代码 <templat…...
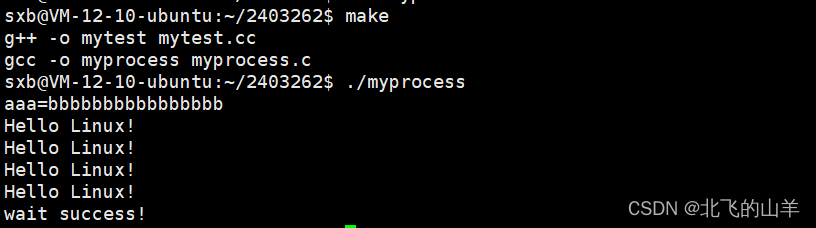
【Linux】详解进程程序替换
一、替换原理 用fork创建子进程后执行的是和父进程相同的程序(但有可能执行不同的代码分支),子进程往往要调用一种exec函数以执行另一个程序。当进程调用一种exec函数时,该进程的用户空间代码和数据完全被新程序替换,从新程序的启动例程开始执…...

vue中使用jsmind生成脑图
项目部分参数: vue:2.6.10 node:16.20.0 1、使用命令行安装jsmind: npm i jsmind -S 2、在文件中引入jsmind,并编写渲染jsmind的代码:: <template><!-- jsmind容器 --><divid"jsmi…...
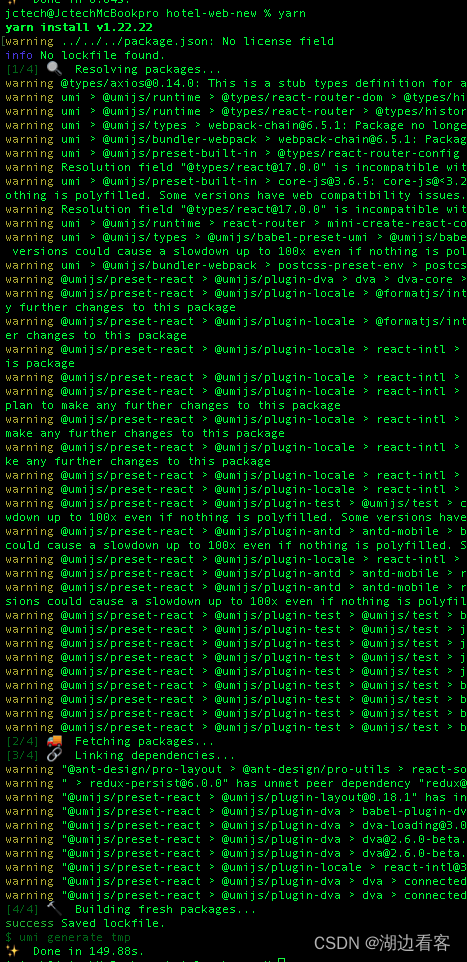
yarn按包的时候报错 ../../../package.json: No license field
运行 yarn config list 然后运行 yarn config set strict-ssl false 之后yarn就成功了...
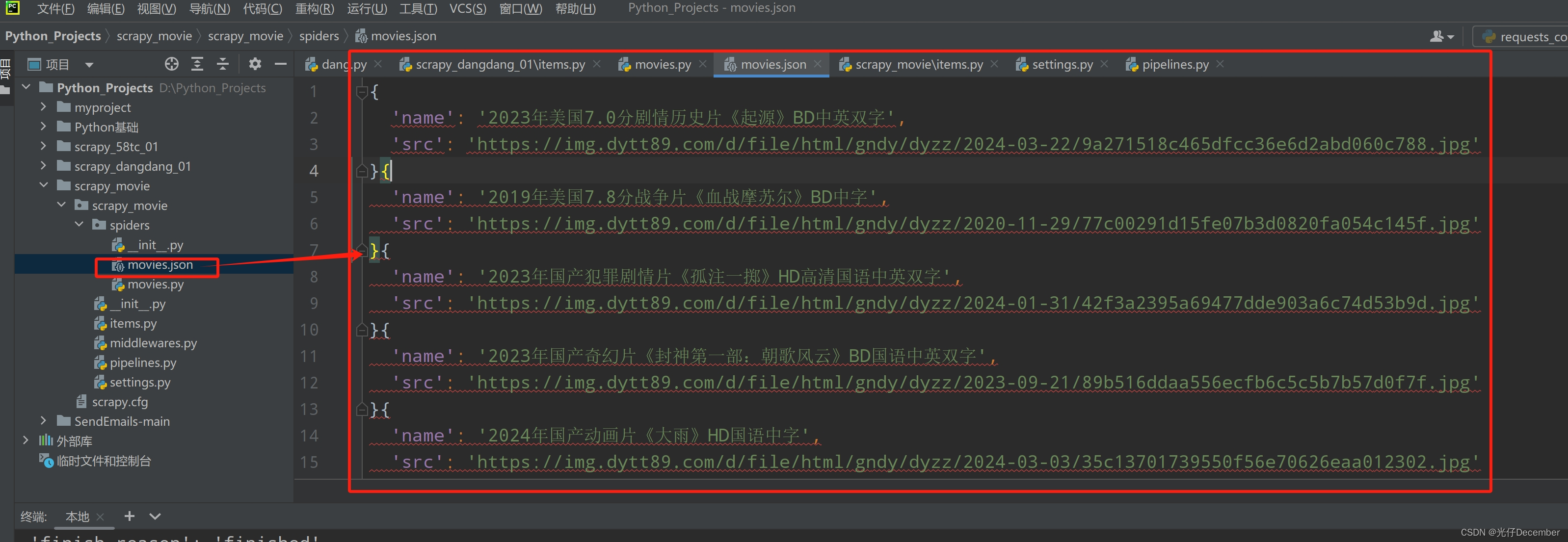
【Python从入门到进阶】51、电影天堂网站多页面下载实战
接上篇《50、当当网Scrapy项目实战(三)》 上一篇我们讲解了使用Scrapy框架在当当网抓取多页书籍数据的效果,本篇我们来抓取电影天堂网站的数据,同样采用Scrapy框架多页面下载的模式来实现。 一、抓取需求 打开电影天堂网站&…...
苹果CMS影视APP源码,二开版本带视频教程
编译app教程 工具下载:Android Studio 官网地址:https://developer.android.google.cn/studio/ 环境设置: 设置中文:https://blog.csdn.net/qq_37131111/article/details/131492844 汉化包找最新的下载就行了,随便下载…...

Zigbee技术在智能农业领域的应用研究
Zigbee技术在智能农业领域的应用研究 **摘要:**随着现代信息技术的飞速发展,智能农业已成为当今农业发展的新趋势。Zigbee技术作为一种低功耗、低成本的无线通信技术,在智能农业领域具有广泛的应用前景。本文深入分析了Zigbee技术的原理和特…...

Spring Cloud Gateway 中GET请求能正常访问,POST请求出现Unable to handle DataBuffer
报错信息如下: java.lang.IllegalArgumentException: Unable to handle DataBuffer of type class org.springframework.http.server.reactive.UndertowServerHttpRequest$UndertowDataBufferat org.springframework.cloud.gateway.filter.NettyRoutingFilter.getB…...

什么是git? 初步认识git 如何使用git
Git是什么? Git 是分布式版本控制系统,可以有效,高速地处理从很小到非常大地项目版本管理,分布式相比于集中式的最大区别在于开发者可以提交到本地,每个开发者可以通过克隆,在本地机器上拷贝一个完整的Git …...
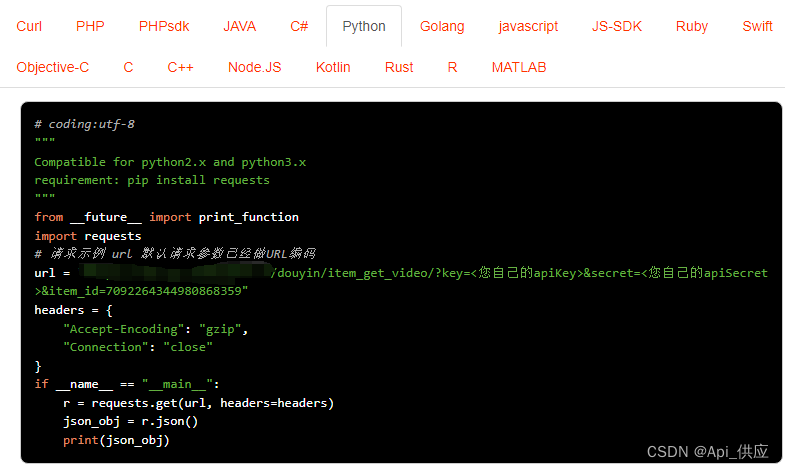
Douyin视频详情数据API接口(视频详情,评论)
抖音官方并没有直接提供公开的视频详情数据采集API接口给普通用户或第三方开发者。抖音的数据采集通常受到严格的限制,以保护用户隐私和平台安全。 请求示例,API接口接入Anzexi58 如果您需要获取抖音视频详情数据,包括评论、点赞等ÿ…...
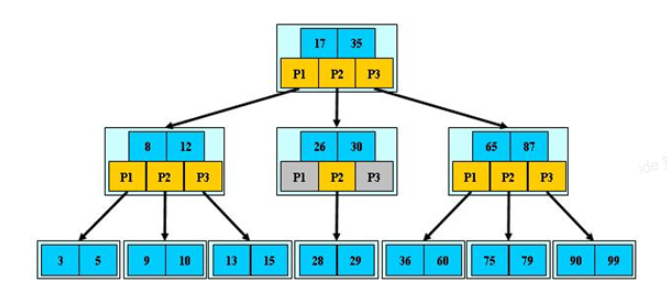
MySQL 索引:索引为什么使用 B+树?
Hash 索引不支持顺序和范围查询; 二叉查找树(BST):解决了排序的问题,极端情况下可能会退化成线性链表,查询效率急剧下降; 平衡二叉树(AVL) :通过旋转解决了平衡的问题,但是旋转操作效率太低&am…...

2024年第四届天府杯全国大学生数学建模竞赛B题思路
B题:新质生产力引领下的企业生产与发展策略优化 问题背景 随着技术的飞速发展,新质生产力如人工智能、大数据分析、物联网等技术被广泛应用于生产和服务过程中,极大地提高了生产效率和产品质量,改变了传统的生产与经营模式。一家…...

c++部分题
const关键字与宏定义的区别是什么? const关键字和宏定义在功能上有相似之处,但在实现和使用上有很大的区别。 作用域和类型安全性: const关键字定义的常量具有作用域和类型安全性。它们的作用域仅限于声明它们的块,并且在编译时会…...

验证回文串
如果在将所有大写字符转换为小写字符、并移除所有非字母数字字符之后,短语正着读和反着读都一样。则可以认为该短语是一个 回文串 。 字母和数字都属于字母数字字符。 给定一个字符串 s,如果它是 回文串 ,返回 true ;否则&#…...
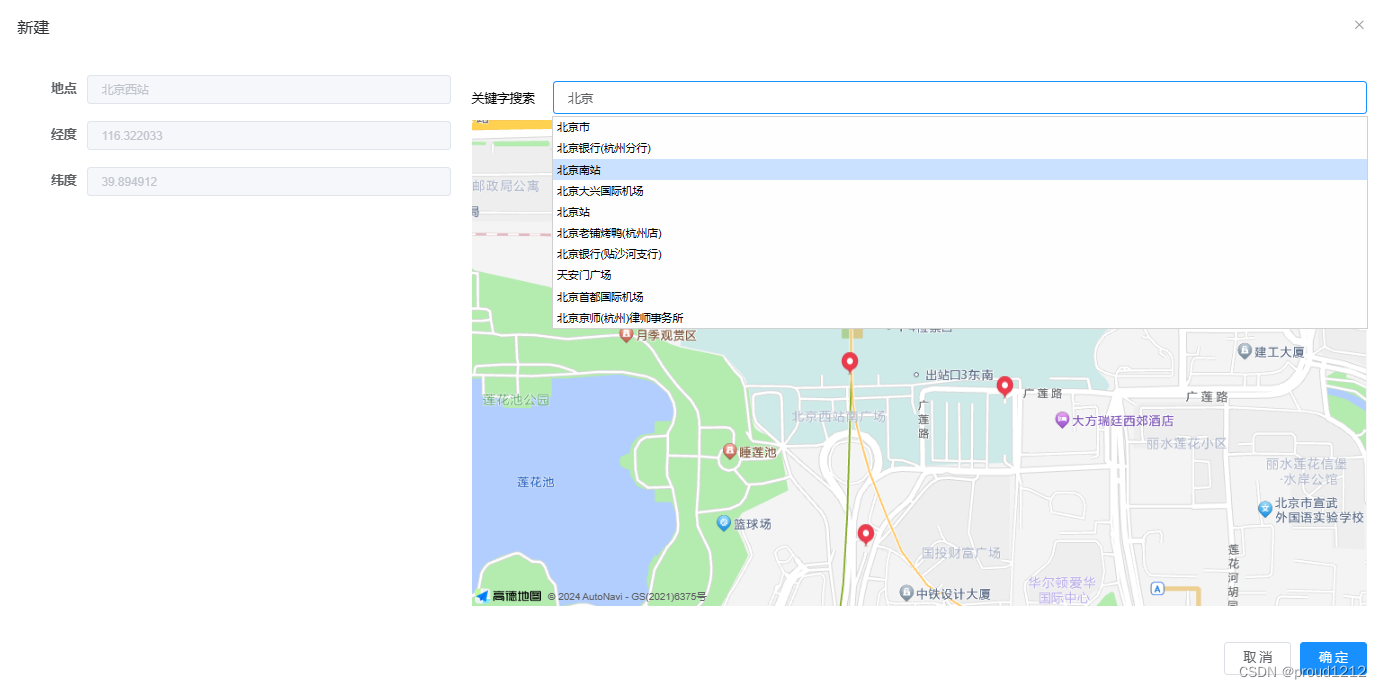
vue2高德地图选点
<template><el-dialog :title"!dataForm.id ? 新建 : isDetail ? 详情 : 编辑" :close-on-click-modal"false" :visible.sync"show" class"rv-dialog rv-dialog_center" lock-scroll width"74%" :before-close&q…...

Gitflow:一种依据 Git 构建的分支管理工作流程模式
文章目录 前言Gitflow 背景Gitflow 中的分支模型Gitflow 的版本号管理简单模拟 Gitflow 工作流 前言 Gitflow 工作流是一种版本控制流程,主要适用于较大规模的团队。这个流程在团队中进行合作时可以避免冲突,并能快速地完成项目,因此在很多软…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...
