后端之卡尔曼滤波
后端之卡尔曼滤波
前言
在很久之前,人们刚结束信息传递只能靠信件的时代,通信技术蓬勃发展,无线通信和有线通信走进家家户户,而著名的贝尔实验室就在这个过程做了很多影响深远的研究。为了满足不同电路和系统对信号的需求,比如去除噪声,或者区分不同频率的信号,滤波器就诞生了,而贝尔实验室就是这一领域研究的先行者。早期的滤波器是电子滤波器,是由电阻,电感,电容等电子元件组成的物理电路,其电路图大概长这样:
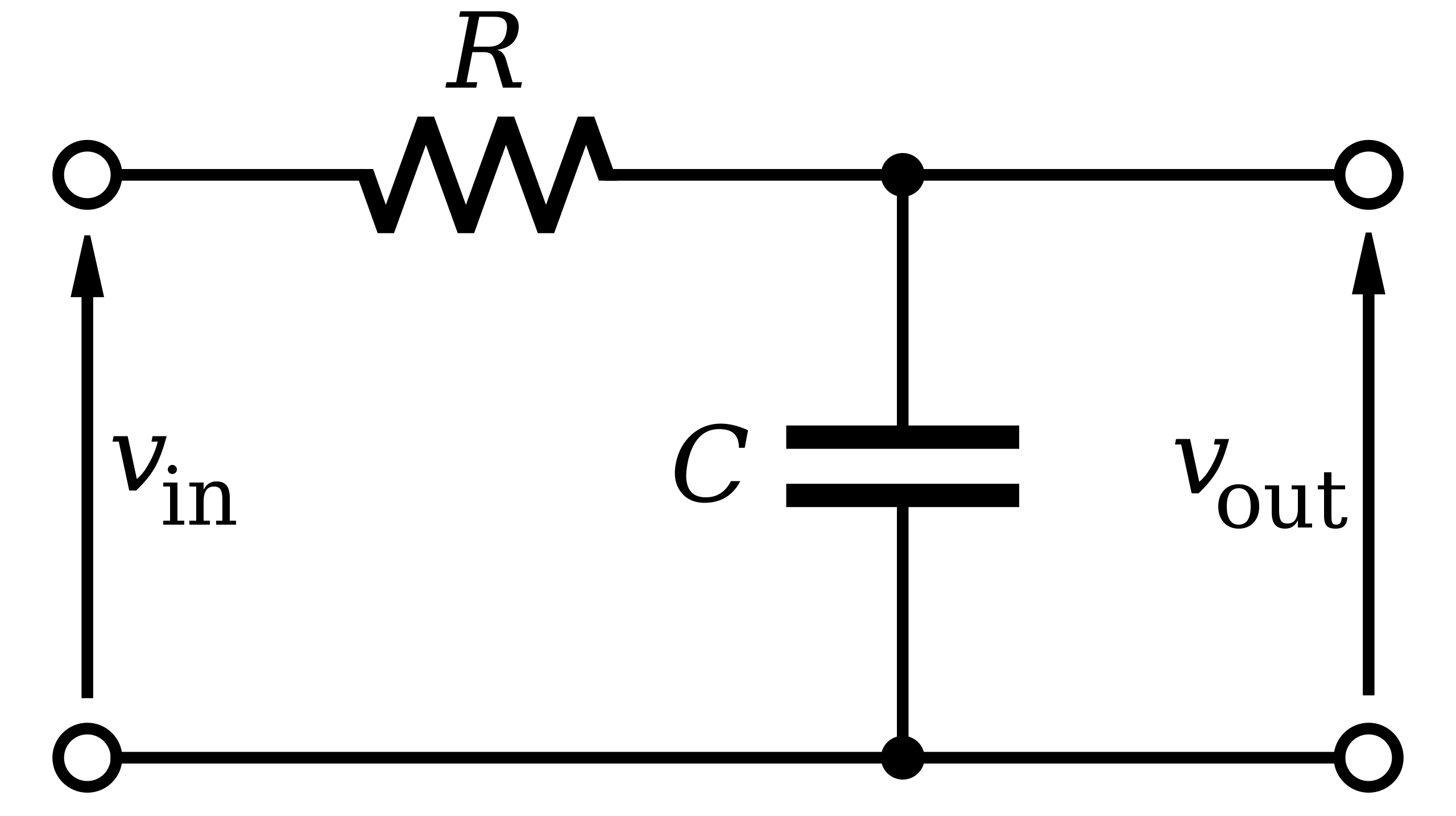
这个是由一个电容和一个电阻组成的RC滤波器。而装在实际家电或者设备中的滤波器大概如下图,这个是一个包含高通和低通滤波器的信号分离装置。
随着技术的发展(主要是计算机的兴起),相比于处理原始模拟信号,人们更愿意处理数字信号,这可以带来更高的处理速度,更低的成本和更高的精度,于是,数字滤波器诞生了。数字滤波器是对数字信号进行滤波处理以得到期望的响应特性的离散时间系统。这时候数字模拟器还是依靠基本的一些电路元件比如寄存器,延时器,加法器等,但其工作的领域已变为经过数模转换器转化后的数字信号域了,后面广泛用于收音机,蜂窝电话等设备中。
数字滤波器早期主要处理信号,而信号都是一些波形,这也是滤波的由来。后面随着人们对滤波器的扩展,出现了另外一种形式的数字滤波器,其工作过程包含状态空间模型,称为状态空间滤波器,状态空间滤波器的一个典型例子是Rudolf Kalman在1960年提出的卡尔曼滤波器。这时候虽然没有了波,主要是空间状态,但按传统,这个名称还是保留了下来。
最后,随着计算机的发展,中央处理器(CPU)集成了各种计算单元,所有计算任务都可以交给它,数字滤波器就不用单独保留如寄存器,加法器等元件了,在保留了算法原理和流程之后羽化成仙,成为了滤波算法。
卡尔曼滤波算法推导简明版
发明了卡尔曼滤波算法的人,叫做鲁道夫·埃米尔·卡尔曼,是一个匈牙利人。
卡尔曼滤波是基于马尔科夫假设的,即下一时刻状态只与上一时刻有关。其主要针对于线性高斯系统,计算的流程如下:
假设状态 X \mathbf{X} X的转移方程为:

其中 F k \mathbf{F}_{k} Fk为状态转移矩阵,而 P k \mathbf{P}_{k} Pk为 X k \mathbf{X}_{k} Xk的方差
X \mathbf{X} X只表示自身的状态,另外一些系统还会有外部控制因数,比如火车减速时,速度是状态量,但可以有刹车装置进行减速,如果系统存在这部分控制因数,需要把这部分加到状态转移中:
x ^ k = F k x ^ k − 1 + B u k P k = F k P k − 1 F k T \begin{aligned} \hat{\mathbf{x}}_{k} & =\mathbf{F}_{k} \hat{\mathbf{x}}_{k-1} +Bu_k\\ \mathbf{P}_{k} & =\mathbf{F}_{\mathbf{k}} \mathbf{P}_{k-1} \mathbf{F}_{k}^{T} \end{aligned} x^kPk=Fkx^k−1+Buk=FkPk−1FkT
另外, X \mathbf{X} X中包含环境的一些未知变量,我们假设为噪声,同时噪声分布假设服从高斯分布,于是有如下方程:
x ^ k = F k x ^ k − 1 + B u k + w k P k = F k P k − 1 F k T + R \begin{aligned} \hat{\mathbf{x}}_{k} & =\mathbf{F}_{k} \hat{\mathbf{x}}_{k-1} +Bu_k +w_k\\ \mathbf{P}_{k} & =\mathbf{F}_{\mathbf{k}} \mathbf{P}_{k-1} \mathbf{F}_{k}^{T} +R \end{aligned} x^kPk=Fkx^k−1+Buk+wk=FkPk−1FkT+R
卡尔曼滤波中,还需要使用观测方程来更新,一般观测方程是需要从状态变为观测量的,即需要有一个观测量到状态的转换,但很多时候这个转换方程都没有,但这并不影响我们假设,如果没有转换方程,到时候直接把转换矩阵设为单位矩阵就行,那现在假设观测方程为:
z k = H ∗ x k + v k z_k = H*x_k+v_k zk=H∗xk+vk
其中 H H H为观测方程, v k v_k vk为观测的噪声分布,假设其服从 v k ∼ N ( 0 , Q ) v_k\sim N\left(0,Q\right) vk∼N(0,Q),即零均值,方差为Q的高斯分布:
到这里,需要说明一点,上一次滤波的结果,会作为下一次滤波的初始值,即由上一次后验概率,通过状态转移矩阵与控制向量,变为目前的先验值,所以原来的观测方程需要变为:
x ^ k ˉ = F k x ^ k − 1 + B u k + w k P k ˉ = F k P k − 1 F k T + R \begin{aligned} \hat{\mathbf{x}}_{\bar{k}} & =\mathbf{F}_{k} \hat{\mathbf{x}}_{k-1} +Bu_k +w_k\\ \mathbf{P}_{\bar{k}} & =\mathbf{F}_{\mathbf{k}} \mathbf{P}_{k-1} \mathbf{F}_{k}^{T} +R \end{aligned} x^kˉPkˉ=Fkx^k−1+Buk+wk=FkPk−1FkT+R
其中下标不带横杠的,表示后验值,带横杠的,代表先验值,这样就由上一时刻的最优估计,得到了当前预测的先验状态及先验方差。
对于观测方程,其方差主要由观测方差决定,即:
P z k = R P_{z_k} = R Pzk=R
zk的均值为Hxk,即zk服从N(Hxk,R)的分布。
这两个分布都是高斯分布,一个是状态的先验分布,一个是传感器测量的分布,这个测量与xk的状态也有关,现在要求这两个分布的联合分布,并求其最大值,很简单,把两个分布乘起来,由于高斯分布的乘积,还是高斯分布,取其均值处,就是概率最大的状态。

乘积的部分,就是所说的状态更新,首先由高斯分布的公式可得:
N ( x , μ , σ ) = 1 σ 2 π e − ( x − μ ) 2 2 σ 2 \mathcal{N}(x, \mu, \sigma)=\frac{1}{\sigma \sqrt{2 \pi}} e^{-\frac{(x-\mu)^{2}}{2 \sigma^{2}}} N(x,μ,σ)=σ2π1e−2σ2(x−μ)2
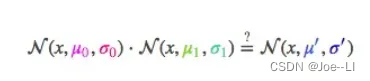
那么两个分布相乘,系数结果为:
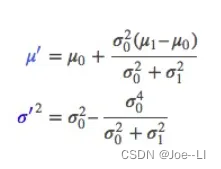
其中均值u就是概率最大时的值,σ就是方差,其中这个式子就是最后我们要求的,但这个式子有点复杂,于是用一个系数化简为:
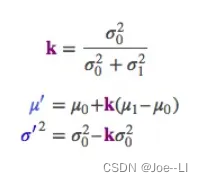
其中k称为卡尔曼增益,u0为预测值,u1为观测。可以看到,k为0到1之间的数,分子为预测的方差,如果预测方差越大,则越向观测值靠拢,如果预测方差越小,则越向预测值靠拢。
截至目前,我们有用矩阵 ( μ 0 , Σ 0 ) = ( H k x ^ k , H k P k H k T ) \left(\mu_0, \Sigma_0\right)=\left(H_k \hat{x}_k, H_k P_k H_k^T\right) (μ0,Σ0)=(Hkx^k,HkPkHkT)预测的分布,有用传感器读数 ( μ 1 , Σ 1 ) = ( z ⃗ k , R k ) \left(\mu_1, \Sigma_1\right)=\left(\vec{z}_k, R_k\right) (μ1,Σ1)=(zk,Rk)预测的分布。把它们代入上节的矩阵等式中:
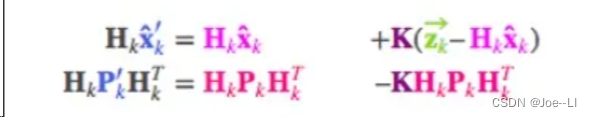
相应的,卡尔曼增益就是:
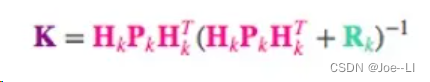
两个式子左边都有不少Hk矩阵,同时把这个矩阵去掉,则K变为:
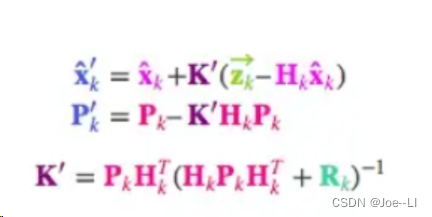
于是,我们得到最后卡尔曼更新的公式:
K k = P k − H T H P k − H T + R x ^ k = x ^ k ˉ + K k ( z k − H x ^ k ˉ ) P k = ( I − K k H ) P k ˉ \begin{array}{c} K_{k}=\frac{P_{k}^{-} H^{T}}{H P_{k}^{-} H^{T}+R} \\ \hat{x}_{k}=\hat{x}_{\bar{k}}+K_{k}\left(z_{k}-H \hat{x}_{\bar{k}}\right) \\ P_{k}=\left(I-K_{k} H\right) P_{\bar{k}} \end{array} Kk=HPk−HT+RPk−HTx^k=x^kˉ+Kk(zk−Hx^kˉ)Pk=(I−KkH)Pkˉ
其中计算K的都是使用先验方差,R为传感器方差。
Zk为实际观测值,Hxk为预测的观测值。
最后使用K及先验方差,得到后验方差及后验均值。
参考链接:
https://zhuanlan.zhihu.com/p/39912633
https://www.guyuehome.com/
相关文章:
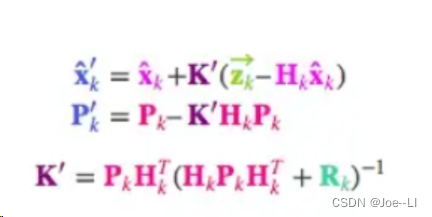
后端之卡尔曼滤波
后端之卡尔曼滤波 前言 在很久之前,人们刚结束信息传递只能靠信件的时代,通信技术蓬勃发展,无线通信和有线通信走进家家户户,而著名的贝尔实验室就在这个过程做了很多影响深远的研究。为了满足不同电路和系统对信号的需求&#…...
Docker 夺命连环 15 问
目录 什么是Docker? Docker的应用场景有哪些? Docker的优点有哪些? Docker与虚拟机的区别是什么? Docker的三大核心是什么? 如何快速安装Docker? 如何修改Docker的存储位置? Docker镜像常…...
2024最新版克魔助手抓包教程(9) - 克魔助手 IOS 数据抓包
引言 在移动应用程序的开发中,了解应用程序的网络通信是至关重要的。数据抓包是一种很好的方法,可以让我们分析应用程序的网络请求和响应,了解应用程序的网络操作情况。克魔助手是一款非常强大的抓包工具,可以帮助我们在 Android …...

Spring Boot 防止XSS攻击
XSS 跨站脚本工具(cross 斯特scripting),为不和层叠样式表(cascading style sheets,CSS)的缩写混淆,故将跨站脚本攻击缩写为XSS。恶意攻击者往web页面里插入恶意ScriptScript代码,当用户浏览该页…...

aidl文件生成Java、C++[android]、C++[ndk]、Rust接口
目录 前言一、Java二、C[android]三、C[ndk]四、Rust接口 前言 在 Android 开发中,AIDL 文件通常会被自动编译,生成对应语言的接口文件。对于应用层 Java 开发者来说,使用 AIDL 和 Binder 封装的接口可以让他们更加专注于应用逻辑࿰…...

多源统一视频融合可视指挥调度平台VMS/smarteye系统概述
系统功能 1. 集成了视频监控典型的常用功能,包括录像(本地录像、云端录像(录像计划、下载计划-无线导出)、远程检索回放)、实时预览(PTZ云台操控、轮播、多屏操控等)、地图-轨迹回放、语音对讲…...

PyTorch简介:与TensorFlow的比较
PyTorch简介:与TensorFlow的比较 一、PyTorch框架概述 PyTorch是一个开源的机器学习库,广泛用于计算机视觉和自然语言处理。由Facebook的人工智能研究团队开发,它以其灵活性和动态计算图而闻名。 主要特点 动态计算图:PyTorch…...
虚拟机-从头配置Ubuntu18.04(包括anaconda,cuda,cudnn,pycharm,ros,vscode)
最好先安装anaconda后cuda和cudnn,因为配置环境的时候可能conda会覆盖cuda的路径(不确定这种说法对不对,这里只是给大家的建议) 准备工作: 1.Ubuntu18.04,x86_64,amd64 虚拟机下载和虚拟机Ubu…...

uniApp使用XR-Frame创建3D场景(8)粒子系统
上篇文章讲述了如何将XR-Frame作为子组件集成到uniApp中使用 本片我们详细讲解一下xr-frame的粒子系统 先看源码 <xr-scene render-system"alpha:true" bind:ready"handleReady"> <xr-node visible"{{sec8}}"><xr-asset-load t…...

【JMeter入门】—— JMeter介绍
1、什么是JMeter Apache JMeter是Apache组织开发的基于Java的压力测试工具,用于对软件做压力测试。它最初被设计用于Web应用测试,但后来扩展到其他测试领域。 (Apache JMeter是100%纯JAVA桌面应用程序)Apache JMeter可以用于对静…...

C# 多线程编程:线程锁与无锁并发
文章目录 前言一、锁的基本概念1.1 什么是锁?1.2 为什么需要锁?1.3 锁的作用原理 二、线程锁的类型2.1 自旋锁(Spin Lock)2.2 互斥锁(Mutex)2.3 混合锁(Hybrid Lock)2.4 读写锁&…...

React.FC
React.FC 是 React 中的一个类型别名,代表“函数组件”。它是一个接受 props(属性)并返回 JSX 元素的函数。 type React.FC<P {}> (props: P) > ReactElement | null;其中:P 是一个可选的泛型类型参数,表示…...

使用pytorch构建一个无监督的深度卷积GAN网络模型
本文为此系列的第二篇DCGAN,上一篇为初级的GAN。普通GAN有训练不稳定、容易陷入局部最优等问题,DCGAN相对于普通GAN的优点是能够生成更加逼真、清晰的图像。 因为DCGAN是在GAN的基础上的改造,所以本篇只针对GAN的改造点进行讲解,其…...

[AI]文心一言出圈的同时,NLP处理下的ChatGPT-4.5最新资讯
AI文心一言出圈的同时,NLP处理下的ChatGPT-4.5最新资讯 1.背景介绍 随着人工智能技术的不断发展,自然语言处理(NLP)技术在近年来取得了显著的进步。其中,聊天机器人技术作为NLP领域的一个重要应用,已经广…...
)
vue.js设计与实现(分支切换与cleanup)
如存在三元运算符时,怎么处理 // 原始数据 const data { text: hello world,ok:true}// 副作用函数存在三元运算符 effect(function effectFn(){document.body.innerText obj.ok ? obj.text : not })// 理解如此,obj.ok和obj.text都会绑定effectFn函…...
206基于matlab的无人机航迹规划(UAV track plannin)
基于matlab的无人机航迹规划(UAV track plannin)。输入输出参数包括 横滚、俯仰、航向角(单位:度);横滚速率、俯仰速率、航向角速率(单位:度/秒);飞机运动速度——X右翼、…...

【Linux 】查看veth-pair对的映射关系
1. 查看当前存在的ns ip netns add netns199 //新建一个命名空间 # ip netns show netns199 (id: 3)可以看到一个名称叫做netns199 的命名空间,其 id为3 2. 创建一个对,并加入其中一个到其他命名空间中 $ sudo ip link add veth100 type veth peer n…...
Cisco Firepower FMCv修改管理Ip方法
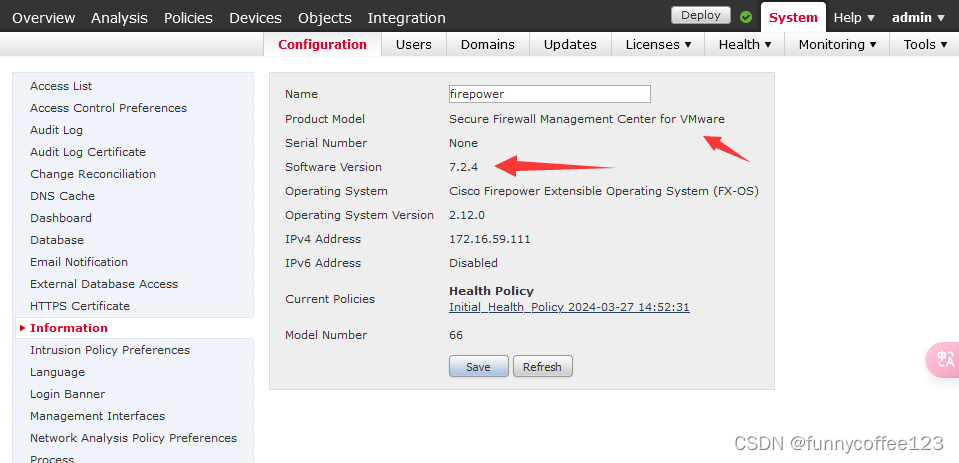
FMCv 是部署在VMWARE虚拟平台上的FMC 部署完成后,如何修改管理IP 1 查看当前版本 show version 可以看到是for VMware 2 修改管理IP步骤 2.1 进入expert模式 expert2.2 进入超级用户 sudo su并输入密码 2.3 查看当前网卡Ip 2.4 修改Ip 命令: /…...
PHP开发全新29网课交单平台源码修复全开源版本,支持聚合登陆易支付
这是一套最新版本的PHP开发的网课交单平台源代码,已进行全开源修复,支持聚合登录和易支付功能。 项目 地 址 : runruncode.com/php/19721.html 以下是对该套代码的主要更新和修复: 1. 移除了论文编辑功能。 2. 移除了强国接码…...
【Web前端】CSS基本语法规范和引入方式常见选择器用法常见元素属性
一、基本语法规范 选择器 {一条/N条声明} 选择器决定针对谁修改 (找谁) 声明决定修改什么.。(干什么) 声明的属性是键值对.。使用 : 区分键值对, 使用 : 区分键和值。 <!DOCTYPE html> <html lang"en"> <head>&…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...
