在Isaac-sim中弧度转四元数以及四元数转弧度的问题
问题:
在Isaac-sim中如果采用set_world_pose()和get_world_pose()得到的都是四元数,如何将弧度转四元数,或者将四元数转为弧度是需要解决的一个问题,
这里的弧度是以x轴为0度,y轴为90度,逆时针方向逐渐增大;
解决方案:
采用scipy.spatial.transform中的Rotation库,进行转换;
在转换的时候涉及到角度的变换,
即如果直接采用Rotation.from_euler(‘x’, angle_rad2, degrees=False)进行转换,得到的是以x轴负方向为0度,y轴为90度,顺时针方向逐渐增大;
因此需要在rad_to_quaternion函数中通过angle_rad2 = -angle_rad + math.pi方法进行转换,同样的在quaternion_to_angle函数中通过angle_rad = -angle_rad + math.pi将转换回来。
import math
from scipy.spatial.transform import Rotation
import torchdef rad_to_quaternion(angle_rad):if angle_rad > math.pi:angle_rad -= 2 * math.pielif angle_rad < -math.pi:angle_rad += 2 * math.piangle_rad2 = -angle_rad + math.pirotation = Rotation.from_euler('x', angle_rad2, degrees=False)# print("rotation.as_quat()=%s" % (str(rotation.as_quat())))quaternion = rotation.as_quat()[:] # 将旋转矩阵转换为四元数return quaternion, angle_rad, angle_rad2def quaternion_to_angle(quaternion):rotation = Rotation.from_quat(quaternion)euler_angles = rotation.as_euler('xyz')angle_rad = euler_angles[0]angle_rad = -angle_rad + math.piif angle_rad > math.pi:angle_rad -= 2 * math.pielif angle_rad < -math.pi:angle_rad += 2 * math.pireturn angle_radfor i in range(361):rad = math.radians(i)quaternion, rad_ori, rad_new = rad_to_quaternion(rad)rad_bak = quaternion_to_angle(quaternion)theta0 = math.degrees(rad_ori)theta1 = math.degrees(rad_new)theta2 = math.degrees(rad_bak)print("原始角度为%s,经过变换后角度为%s,转换后的角度为%s"%(str(round(theta0)), str(round(theta1)), str(round(theta2))))# rad_new = math.floor(rad_new * 10000) / 10000# rad_bak = math.floor(rad_bak * 10000) / 10000# if rad_new != rad_bak:# print("出错了rad_new=%s, rad_bak=%s"%(str(rad_new), str(rad_bak)))# print("rad=%.4f, rad_bak=%.4f"%(rad, rad_bak))相关文章:

在Isaac-sim中弧度转四元数以及四元数转弧度的问题
问题: 在Isaac-sim中如果采用set_world_pose()和get_world_pose()得到的都是四元数,如何将弧度转四元数,或者将四元数转为弧度是需要解决的一个问题, 这里的弧度是以x轴为0度,y轴为90度,逆时针方向逐渐增大…...

【计算机网络】高级IO模型
高级IO模型 一、 理解 IO二、认识五种高级 IO 模型1. 阻塞 IO2. 非阻塞IO3. 信号驱动 IO4. IO 多路转接5. 异步 IO 三、高级 IO 重要概念1. 阻塞和非阻塞2. 同步通信和异步通信 四、非阻塞 IOfcntl 一、 理解 IO 当我们调用系统接口 write、read 的时候,本质是把数…...

LabVIEW电动汽车直流充电桩监控系统
LabVIEW电动汽车直流充电桩监控系统 随着电动汽车的普及,充电桩的安全运行成为重要议题。通过集成传感器监测、单片机技术与LabVIEW开发平台,设计了一套电动汽车直流充电桩监控系统,能实时监测充电桩的温度、电压和电流,并进行数…...
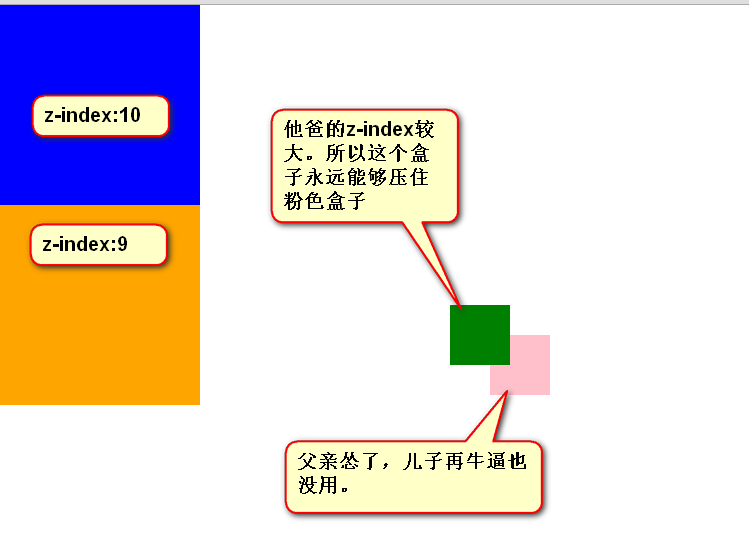
前端学习<二>CSS基础——08-CSS属性:定位属性
CSS的定位属性有三种,分别是绝对定位、相对定位、固定定位。 position: absolute; <!-- 绝对定位 -->position: relative; <!-- 相对定位 -->position: fixed; <!-- 固定定位 --> 下面逐一介绍。 相对定位 相对定位:让…...
)
88. 合并两个有序数组(javascript)
给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。 请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。 注意:最终,合并后数组…...

机器学习_集成学习_梯度提升_回归_决策树_XGBoost相关概念
目录 1. 机器学习 使用监督吗?什么又是监督学习? 2. 与XGBoost 类似的机器学习方法有哪些? 3. 随机森林方法 和 梯度提升方法 有什么区别? 分别应用于什么场景? 4. 决策树回归方法 和 Gradient Boosting类回归方法…...
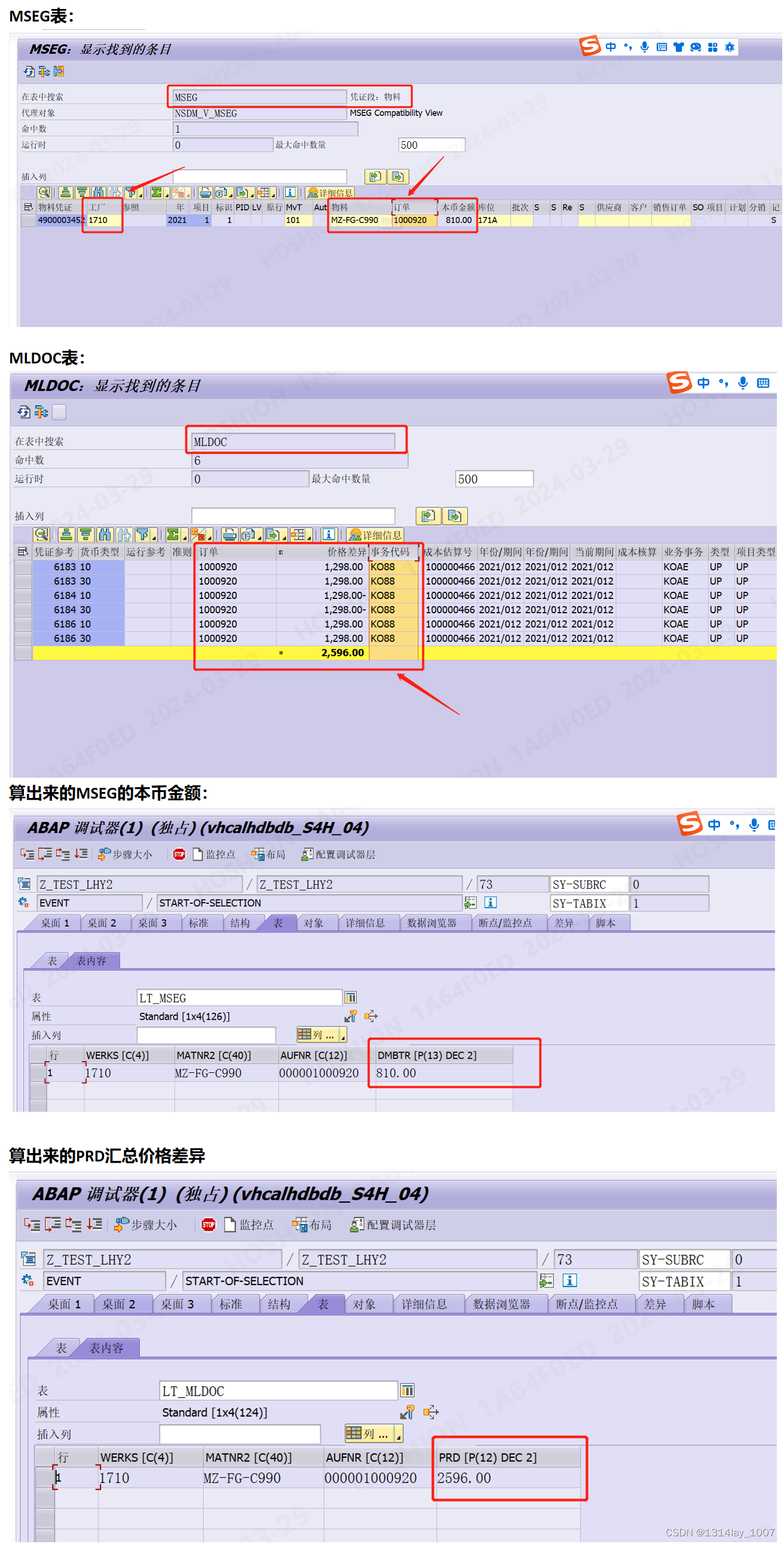
ABAP 字段类型不一样导致相加之后金额错误
文章目录 ABAP 字段类型不一样导致相加之后金额错误写在前面的总结示例程序1汇总MSEG表和MLDOC表 ABAP 字段类型不一样导致相加之后金额错误 写在前面的总结 如果需要不同底表的字段相加的值,那么最好是根据条件去分别算出那些值放在临时内表里面,再去…...

【L1距离和L2距离】Manhattan Distance Euclidean Distance 解释和计算公式
距离度量 特征空间中两个实例点的距离可以反映出两个实力点之间的相似性程度,使用的距离可以是欧式距离,也可以是其他距离。 欧氏距离(L2距离):最常见的两点之间或多点之间的距离表示法,又称之为欧几里得度量,它定义于…...
自动发卡平台源码优化版,支持个人免签支付
源码下载地址:自动发卡平台源码优化版.zip 环境要求: php 8.0 v1.2.6◂ 1.修复店铺共享连接时异常问题 2024-03-13 23:54:20 v1.2.5 1.[新增]用户界面硬币增款扣款操作 2.[新增]前台对接库存信息显示 3.[新增]文件缓存工具类[FileCache] 4.[新增]库存同…...

如何使用固定公网地址远程连接Python编译器并将运行结果返回到Pycharm
文章目录 一、前期准备1. 检查IDE版本是否支持2. 服务器需要开通SSH服务 二、Pycharm本地链接服务器测试1. 配置服务器python解释器 三、使用内网穿透实现异地链接服务器开发1. 服务器安装Cpolar2. 创建远程连接公网地址 四、使用固定TCP地址远程开发 本文主要介绍如何使用Pych…...
Java设计模式—备忘录模式(快照模式)
定义 备忘录模式提供了一种状态恢复的实现机制,使得用户可以方便地回到一个特定的历史步骤,当新的状态无效或者存在问题时,可以使用暂时存储起来的备忘录将状态复原,很多软件都提供了撤销(Undo)操作&#…...
没学数模电可以玩单片机吗?
我们首先来看一下数电模电在单片机中的应用。数电知识在单片机中主要解决各种数字信号的处理、运算,如数制转换、数据运算等。模电知识在单片机中主要解决各种模拟信号的处理问题,如采集光照强度、声音的分贝、温度等模拟信号。而数电、模电的相互转换就…...

FlinkSQL之Flink SQL Join二三事
Flink SQL支持对动态表进行复杂而灵活的连接操作。 为了处理不同的场景,需要多种查询语义,因此有几种不同类型的 Join。默认情况下,joins 的顺序是没有优化的。表的 join 顺序是在 FROM 从句指定的。可以通过把更新频率最低的表放在第一个…...

某某消消乐增加步数漏洞分析
一、漏洞简介 1) 漏洞所属游戏名及基本介绍:某某消消乐,三消游戏,类似爱消除。 2) 漏洞对应游戏版本及平台:某某消消乐Android 1.22.22。 3) 漏洞功能:增加游戏步数。 4…...
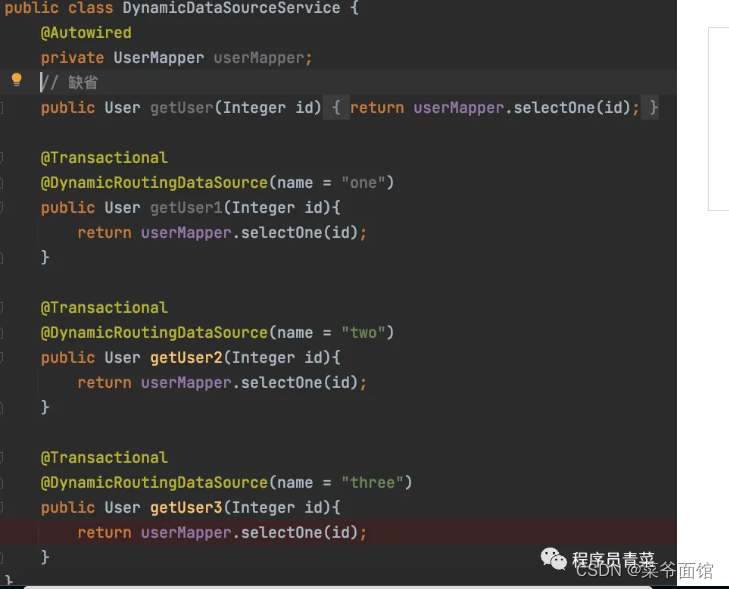
SpringBoot动态数据源实现
一、背景 一个应用难免需要连接多个数据库,像我们系统起码连接了5个以上数据库,AWS RDS主库,ECS自搭MySQL从库,工厂系统三个SQLServer数据库,在线网站MySQL数据库,记得很早以前是用SessionFactory配置&…...

计算机网络常见题(持续更新中~)
1 描述一下HTTP和HTTPS的区别 2 Cookie和Session有什么区别 3 如果没有Cookie,Session还能进行身份验证吗? 4 BOI,NIO,AIO分别是什么 5 Netty的线程模型是怎么样的 6 Netty是什么?和Tomcat有什么区别,特点是什么? 7 TCP的三次…...

富格林:可信招数揭发防备暗箱陷阱
富格林悉知,在风云变幻的金融市场中,炒贵金属是一项具有高收益潜力的投资方式。但投资是风险与收益共存的,因此我们在做单投资过程中需总结可信招数揭发暗箱陷阱,防备受害亏损。以下总结几点可信的投资技巧,希望能够帮…...
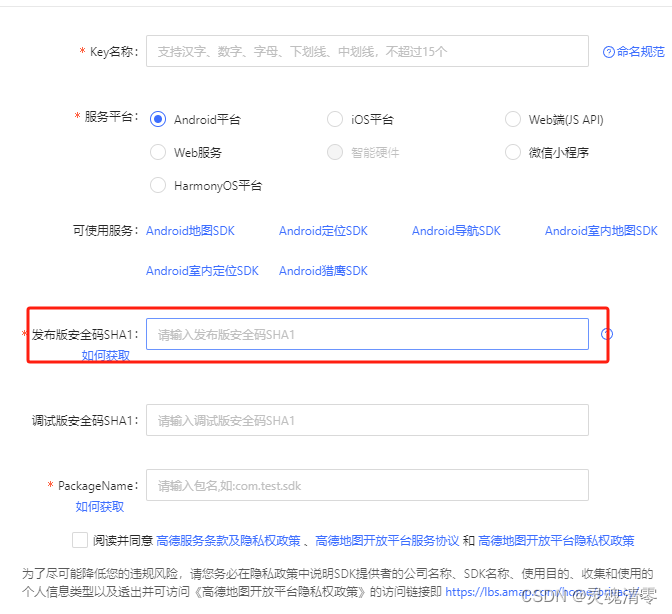
获取高德安全码SHA1
高德开发者平台上给的三种方法 获取安全码SHA1,这里我自己使用的是第三种方法。 1、通过Eclipse编译器获取SHA1 使用 adt 22 以上版本,可以在 eclipse 中直接查看。 Windows:依次在 eclipse 中打开 Window -> Preferances -> Androi…...
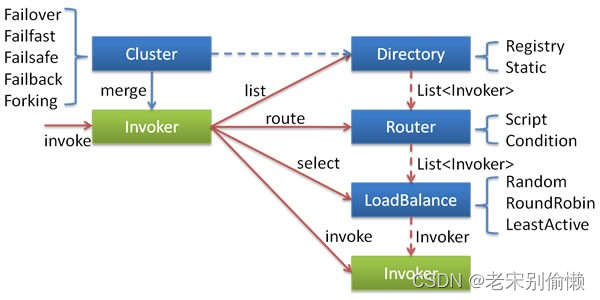
关于RPC
初识RPC RPC VS REST HTTP Dubbo Dubbo 特性: 基于接口动态代理的远程方法调用 Dubbo对开发者屏蔽了底层的调用细节,在实际代码中调用远程服务就像调用一个本地接口类一样方便。这个功能和Fegin很类似,但是Dubbo用起来比Fegin还要简单很多&a…...

pulsar: kafka on pulsar之把pulsar当kafka用
一、下载协议包(要和pulsar版本比较一致) https://github.com/streamnative/kop/releases?q2.8.0&expandedtrue二、在pulsar的根目录创建一个protocols目录,将上述包放到这个目录里 三、编辑broker.conf(如果是集群)或者standalone.con…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...
