数据结构:单调栈和单调队列
文章目录
- 一、单调栈
- 1.1、栈的思想
- 1.2、单调栈
- 1.2.1、单调栈的基本应用:找出数组中每个元素右侧第一个更大的元素
- 1.2.2、单调栈的基本应用:找出数组中每个元素左侧第一个更大的元素
- 1.2.3、单调栈拓展
- 1.2.4、单调栈LeetCode题单
- 二、单调队列
- 2.1、队列的思想
- 2.2、单调队列
- 单调队列的应用:滑动窗口最大值
- 三、单调栈和单调队列的区别
- 示例解释
在学习单调队列或单调栈时,我们要先清楚,为何栈或队列是保持单增或单减,并且这样为何是有效的。比如保持单增,用单调队列的思想考虑的情况下,在遍历的过程中,我们需要解决的问题是寻找第一个比它小的(或者维护窗口中最小的元素),当前元素进队/栈时,如果栈顶或队尾存在比当前元素大的元素时,这些元素都是冗余的,因为当前元素在往后考虑时的作用 会一定更接近往后的元素且更小(更满足我们需要第一个小的要求)并且在单调队列中也更会留在窗口中。(单调栈有不同实现方式和思想,这里只描述了一种,详情请往下看)
一、单调栈
1.1、栈的思想
栈是一种非常直观且广泛应用的数据结构,其主要特点是后进先出(LIFO,Last In, First Out)。想象一下一摞盘子或书籍,你只能从顶部添加或移除它们。栈可以临时存放一些数据,以便于之后逆序访问它,比如进制转换。
浏览器的前后进是个很形象的例子:浏览器允许用户后退和前进浏览过的网页。这可以通过两个栈来实现:一个栈用于后退,另一个用于前进。当你访问新页面时,前进栈清空,当前页面压入后退栈。当你点击后退时,从后退栈中弹出,并将其压入前进栈。前进按钮则相反。
1.2、单调栈
单调栈是一种特殊的栈,其元素按照单调递增或单调递减的顺序排列(根据特殊需求也可以是非减或非增序列)。单调栈用于解决那些需要寻找每个元素左侧或右侧第一个比它大(或小)的元素的问题。当新的元素被尝试加入栈时,会从栈顶开始移除破坏单调性的元素,直到保持栈的单调性为止,然后将新元素入栈。
应用示例:在一个数组中,为每个元素找出其右侧或左侧第一个更大的元素。LeetCode:柱状图中最大的矩形
如果要求的是左侧或右侧的最大/小值(而不是第一个更大/小的),可以用动态规划求解,如LeetCode:接雨水
1.2.1、单调栈的基本应用:找出数组中每个元素右侧第一个更大的元素
使用单调栈解决这个问题的基本思路是遍历数组,对于每个元素,我们想找到它右侧第一个更大的元素。单调栈可以帮助我们追踪已经遍历过的元素,并保持它们的顺序,以便快速找到每个元素的答案。
- 初始化一个空栈,用于存放数组元素的索引。
- 遍历数组中的每个元素:
- 当栈不为空且当前元素大于栈顶索引对应的元素时,表示找到了栈顶元素右侧的第一个更大元素。此时,将栈顶元素出栈,并记录当前元素为栈顶元素右侧第一个更大的元素。
- 将当前元素的索引入栈。
- 对于栈中剩余的元素,它们右侧没有更大的元素。
#include <vector>
#include <stack>
using namespace std;class Solution {
public:vector<int> nextGreaterElement(vector<int>& nums) {int n = nums.size();vector<int> ans(n, -1); // 初始化结果数组,假设每个元素的右侧没有更大的元素stack<int> myStack; // 用于存储索引,栈顶到栈底单调递减for (int i = 0; i < n; ++i) {// 当前元素大于栈顶元素对应的值时,说明找到了一个更大的元素while (!myStack.empty() && nums[i] > nums[myStack.top()]) {ans[myStack.top()] = nums[i]; // 更新栈顶元素的下一个更大元素myStack.pop(); // 弹出栈顶元素}// 将当前元素的索引入栈myStack.push(i);}// 对于栈中剩余的元素,它们的右侧没有更大的元素,ans中已经预设为-1,因此无需再操作return ans;}
};
1.2.2、单调栈的基本应用:找出数组中每个元素左侧第一个更大的元素
可以直接使用1.2.1的方法反向扫描,反向扫描的右边实际上是原来的左边。如果在一个问题中同时求这俩,那用反向扫描肯定是最便捷的方式。 也可以直接从左往右扫描,如果栈顶元素比当前元素小则弹栈,直到遇到比当前元素大的则是左侧第一个更大元素。(这和单调队列的弹出队列的方式很像,因为比它小的不仅对以后没用,对当前元素来说也没用。)
#include <vector>
#include <stack>
using namespace std;class Solution {
public:vector<int> leftGreaterElement(vector<int>& nums) {int n = nums.size();vector<int> ans(n, -1); // 初始化结果数组,假设每个元素的左侧没有更大的元素stack<int> myStack; // 用于存储索引,栈顶到栈底单调递减for (int i = 0; i < n; ++i) {// 当前元素大于栈顶元素对应的值时,说明当前元素是遍历到目前为止的最大元素// 这里不需要像找右侧元素那样进行元素的更新,因为我们关心的是左侧元素while (!myStack.empty() && nums[i] >= nums[myStack.top()]) {myStack.pop(); // 弹出栈顶元素}// 如果栈不为空,说明找到了当前元素左侧的第一个更大元素if (!myStack.empty()) {ans[i] = nums[myStack.top()];}// 将当前元素的索引入栈myStack.push(i);}return ans;}
};1.2.3、单调栈拓展
单调栈的一次遍历不仅仅只能解决找到第一个更小的问题,它一次遍历就能找到左右两边的信息,不过有一边是等高的,有时候我们可以利用这一个特点来处理问题。这样的拓展使用需要在不同问题中发现,如1.2.4列出的题单。
for (int i = 0; i < n; ++i) {//递减序while (!myStack.empty() && nums[i] >= nums[myStack.top()]) {//右侧if(nums[i]>nums[myStack.top()]) 则能找到右侧更大,但可能出现相等的情况,可能相等的情况并不影响答案//所以需要有这种考虑和想法,以便于后面遇到这样的问题能够思考到,然后利用起来myStack.pop(); // 弹出栈顶元素}if (!myStack.empty()) {left_max[i] = nums[myStack.top()];//左边更大一定是正确的}myStack.push(i);
}
1.2.4、单调栈LeetCode题单
二、单调队列
2.1、队列的思想
队列是一种先进先出(First In, First Out,FIFO)的数据结构,其工作原理类似于日常生活中的排队等待。在队列中,元素从一端(通常称为队尾)添加,从另一端(称为队头)进行移除。这种结构确保了元素被处理的顺序正是它们被添加到队列中的顺序,就像人们在商店结账处排队一样:先来的人先得到服务,新来的人排在队伍的末尾。
2.2、单调队列
单调队列是一种特殊的队列,其元素同样按照单调递增或单调递减的顺序排列。不同于单调栈,单调队列支持在两端进行操作:在队列的一端添加元素,在另一端移除元素。这种结构适用于滑动窗口类的问题,其中窗口在数据序列上滑动,而我们希望快速获取窗口内的最大值或最小值。
应用示例:给定一个数组和一个窗口大小,为每个窗口找出最大值或最小值。
单调队列的应用:滑动窗口最大值
单调队列解决的是另一个问题:给定一个数组和一个窗口大小,为每个窗口找出最大值。单调队列通过维护一个双端队列(Deque),其中保存可能成为当前窗口最大值的元素索引,确保队列是单调递减的。LeetCode求滑动窗口最大值
- 初始化一个空的双端队列(Deque)。
- 遍历数组中的每个元素:
- 移除队列中所有小于当前元素的索引,因为它们不可能是包含当前元素的窗口的最大值。
- 检查队头索引是否已经滑出窗口(即队头索引对应的元素不在当前考虑的窗口内),如果是,将其从队头移除。
- 将当前元素的索引添加到队列尾部。
- 对于每个窗口,队头索引总是对应该窗口的最大值。且队列里总是会有元素(因为至少当前正在遍历的元素一定在窗口中)。
#include <vector>
#include <deque>
using namespace std;class Solution {
public:vector<int> maxSlidingWindow(vector<int>& nums, int k) {deque<int> myque; // 存储的是nums的索引,保证从大到小排列vector<int> ans;for(int i = 0; i < nums.size(); ++i) {// 如果队列不为空且当前元素大于等于队列最后一个元素所对应的值,则弹出队列最后一个元素while(!myque.empty() && nums[i] >= nums[myque.back()]) {myque.pop_back();}// 将当前元素索引加入队列myque.push_back(i);// 确保队列第一个元素始终在当前滑动窗口的范围内if(myque.front() <= i - k) {myque.pop_front();}// 当索引达到窗口大小-1时,开始记录结果if(i >= k - 1) {ans.push_back(nums[myque.front()]);}}return ans;}
};三、单调栈和单调队列的区别
你会发现单调队列和单调栈的区别在于,是否包含一个滑动窗口,单调队列处理的之前的成员可能会"失效",但是单调栈的成员一直不会失效,因此单调队列有一个“失效”出队的操作。单调栈处理的问题中,一旦元素入栈,它们就保持有效,直到被明确地由一个满足特定条件的后来者替代;而单调队列处理的问题中,元素的有效性不仅受到队列中其他元素的影响,还受到它们是否仍然处于考虑的窗口内的影响。
示例解释
假设你有一系列人的身高,你需要找到每个人右侧的第一个更高的人(单调栈),或者在一系列长度为k的连续子序列(即窗口)中找到最高的人(单调队列)。
- 单调栈:当一个新人加入时,如果他比前面的人都高,那么他就成为了前面某些人右侧第一个更高的人。前面比他矮的人都不再重要,因为他们已经找到了比自己高的人。
- 单调队列:对于每个长度为k的窗口,你想快速知道最高的人。当一个新人加入窗口时,如果他比窗口中的某些人高,那么这些比他矮的人就不可能是该窗口的最高者了。但是,窗口滑动时,最高的人可能会离开窗口,所以你需要记录下一个可能最高的人。
通过使用单调栈和单调队列,你可以高效地解决这些问题,而不需要对每个元素或每个窗口进行独立的比较。每个元素进栈(队)一次,出栈(队)一次,因此时间复杂度均为O(n)。
相关文章:

数据结构:单调栈和单调队列
文章目录 一、单调栈1.1、栈的思想1.2、单调栈1.2.1、单调栈的基本应用:找出数组中每个元素右侧第一个更大的元素1.2.2、单调栈的基本应用:找出数组中每个元素左侧第一个更大的元素1.2.3、单调栈拓展1.2.4、单调栈LeetCode题单 二、单调队列2.1、队列的思…...

大模型RAG性能提升路径
大模型相关目录 大模型,包括部署微调prompt/Agent应用开发、知识库增强、数据库增强、知识图谱增强、自然语言处理、多模态等大模型应用开发内容 从0起步,扬帆起航。 大模型应用向开发路径:AI代理工作流大模型应用开发实用开源项目汇总大模…...
—— 边缘检测)
机器视觉学习(九)—— 边缘检测
目录 一、边缘检测 1.1 Canny边缘检测 1.1.1 cv2.Canny函数 1.1.2 Canny边缘检测示例 1.2 角点检测 1.2.1 cv2.goodFeaturesToTrack()函数 1.2.2 OpenCV角点检测示例代码 1.3 直线检测 1.3.1 cv2.HoughLinesP()函数 1.3.2 OpenCV直线检测示例代码 1.4 圆形检测 1.4…...

基于单片机声音分贝采集和显示控制系统设计
**单片机设计介绍,基于单片机声音分贝采集和显示控制系统设计 文章目录 一 概要二、功能设计设计思路 三、 软件设计原理图 五、 程序六、 文章目录 一 概要 基于单片机声音分贝采集和显示控制系统设计,主要目标是实现声音分贝的实时采集、处理以及显示…...
CentOS使用Docker部署Halo并结合内网穿透实现公网访问本地博客
文章目录 1. Docker部署Halo1.1 检查Docker版本如果未安装Docker可参考已安装Docker步骤:1.2 在Docker中部署Halo 2. Linux安装Cpolar2.1 打开服务器防火墙2.2 安装cpolar内网穿透 3. 配置Halo个人博客公网地址4. 固定Halo公网地址 本文主要介绍如何在CentOS 7系统使…...
打造高效自动化渗透测试系统:关键步骤与实践
随着当前网络安全威胁的不断扩展与升级,开展渗透测试工作已经成为广大企业组织主动识别安全漏洞与潜在风险的关键过程。然而,传统的人工渗透测试模式对测试人员的专业能力和经验水平有很高的要求,企业需要投入较大的时间和资源才能完成。在此…...
绿联 部署vocechat,搭建私人聊天服务器,用于小型团队和家庭环境
1、镜像 privoce/vocechat-server:latest 2、安装 2.1、基础设置 重启策略:容器退出时总是重启容器。 2.2、网络 桥接即可。 2.3、存储空间 装载路径:/home/vocechat-server/data不可变更,权限读写。 2.4、端口设置 容器端口3000不可变…...

考研数学|高效刷透汤家凤《1800》经验分享
当然不需要换老师,如果你在基础阶段连汤老师的课都听不进去,那么换其他老师的话,很大可能也是白搭。 如果你现在对于1800还是一筹莫展的话,那么很明显,这反映出前期基础不扎实,没有真正理解和掌握这部分内…...

LLM推理入门指南②:深入解析KV缓存
在本系列文章《LLM推理入门指南①:文本生成的初始化与解码阶段》中,作者对Transformer解码器的文本生成算法进行了高层次概述,着重介绍了两个阶段:单步初始化阶段,即提示的处理阶段,和逐个生成补全词元的多…...
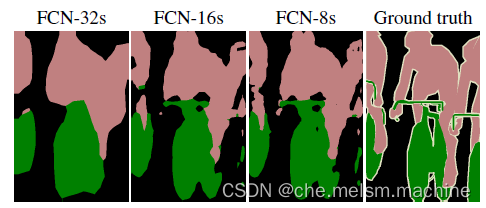
上采样技术在语义分割中的应用
目录 概要 一、概述 二、实现方法 1.转置卷积 2.反池化 3.双线性插值法 三、在经典网络中的的应用 1.U-Net 2.FCN 总结 概要 上采样是用于深度学习中提高语义分割精度的技术,可以实现图像放大和像素级别标注 一、概述 神经网络的基本结构为:…...

linux 组建raid5详细操作
raid5最多运行损坏一个盘,最少3个盘,容量为少一块硬盘的容量之和。 如果硬盘数量较多,比如8块以上,建议用raid6,raid6最多允许两块硬盘损坏。 如果需要 一、安装raid软件 deb包 apt-get install mdadm或dnf包 dnf …...

机器学习概念、步骤、分类和实践
在当今数字化时代,机器学习已经渗透到我们生活的方方面面,从智能手机应用、搜索引擎优化,到自动驾驶汽车、医疗诊断等,其应用无处不在。本文将带您走进机器学习的世界,了解它的基本概念、步骤、分类以及实践应用。 一…...
钉钉服务端API报错 错误描述: robot 不存在;解决方案:请确认 robotCode 是否正确
problem 调用钉钉服务端API,机器人发送群聊消息,后台返回报错信息: 钉钉服务端API报错 错误描述: robot 不存在;解决方案:请确认 robotCode 是否正确; reason 定位: 登录后台,查看机器人是存在查看机器人调用权限接…...

Linux 开发环境以及编译链接
再谈编译链接 C函数重载与编译链接-CSDN博客 之前我已经写过文章简单介绍了编译链接要做的一些操作。现在为了能更好的理解我们平时的开发环境,我会在Linux系统上完整地走一遍流程。 环境描述 我们使用普通用户在Linux上进行操作,先写一段测试代码。 …...

SmartChart的部署以及可能遇见的报错解决方案
简介 数据可视化是一种将数据转化为图形的技术,可以帮助人们更好地理解和分析数据。但是,传统的数据可视化开发往往需要编写大量的代码,或者使用复杂的拖拽工具,不仅耗时耗力,而且难以实现个性化的需求。有没有一种更…...

【Node.js从基础到高级运用】十九、Node.js 捕获错误之“未捕获的异常”
引言 在 Node.js 应用程序中,错误处理是保证应用稳定性和可靠性的关键部分。特别是“未捕获的异常”(uncaught exceptions),如果不妥善处理,很可能会导致整个进程崩溃。在本文中,我们将探讨如何在 Node.js …...

vue 计算属性
基础示例 模板中的表达式虽然方便,但也只能用来做简单的操作。如果在模板中写太多逻辑,会让模板变得臃肿,难以维护。比如说,我们有这样一个包含嵌套数组的对象: const author reactive({name: John Doe,books: [V…...

RedissonLock-tryLock-续期
redisson版本3.16.6 1.什么是看门狗 Redisson提供的分布式锁是支持锁自动续期的,也就是说,如果线程仍旧没有执行完,那么redisson会自动给redis中的目标key延长超时时间,这在Redisson中称之为 Watch Dog 机制。默认情况下&#x…...

MSTP环路避免实验(华为)
思科设备参考:MSTP环路避免实验(思科) 一,技术简介 MSTP(多生成树协议),MSTP解决了STP和RSTP没有考虑vlan的问题,STP和RSTP将所有的vlan共享为一个生成树实例,无法实现…...
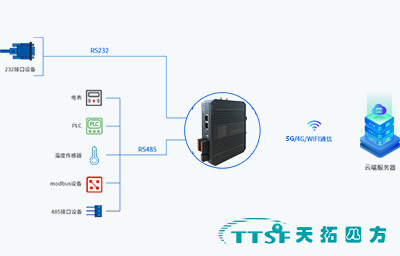
IoT网关在智能制造工厂生产线监控与管理中的应用-天拓四方
随着工业4.0时代的到来,智能制造已成为工业发展的重要方向。IoT网关在智能制造工厂中扮演着关键角色,它能够实现设备间的互联互通、数据的实时采集与处理,以及生产线的智能监控与管理。本案例将详细介绍IoT网关在智能制造工厂生产线监控与管理…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

规则与人性的天平——由高考迟到事件引发的思考
当那位身着校服的考生在考场关闭1分钟后狂奔而至,他涨红的脸上写满绝望。铁门内秒针划过的弧度,成为改变人生的残酷抛物线。家长声嘶力竭的哀求与考务人员机械的"这是规定",构成当代中国教育最尖锐的隐喻。 一、刚性规则的必要性 …...

Mac flutter环境搭建
一、下载flutter sdk 制作 Android 应用 | Flutter 中文文档 - Flutter 中文开发者网站 - Flutter 1、查看mac电脑处理器选择sdk 2、解压 unzip ~/Downloads/flutter_macos_arm64_3.32.2-stable.zip \ -d ~/development/ 3、添加环境变量 命令行打开配置环境变量文件 ope…...

电脑桌面太单调,用Python写一个桌面小宠物应用。
下面是一个使用Python创建的简单桌面小宠物应用。这个小宠物会在桌面上游荡,可以响应鼠标点击,并且有简单的动画效果。 import tkinter as tk import random import time from PIL import Image, ImageTk import os import sysclass DesktopPet:def __i…...
