OKCC的API资源管理平台怎么用?
API资源管理平台,重点是“资源”管理平台,不是API接口管理平台。

天天讯通推出的API资源管理平台,类似昆石的VOS系统,区别是VOS是SIP资源管理系统,我们的API资源管理平台是API资源管理系统(AXB、AX、回拨API)。
那这个平台谁可以用,怎么用?
说这个之前,先清晰一个概念,我们的API资源管理平台有两个层级的账户,运营商账户,及Superadmin账户,和企业账户,同一API资源平台下,仅仅只有一个运营商账户,但可以有多个企业账户。如下图所示,该图为API资源平台的客户关系图,顶级只有运营商,运营商下面可以直接发展多个企业客户,层级只有1级。

注意,企业账户并非只代表终端客户账户,这个企业账户也可以是二手线路商账户。
现在说谁可以用和怎么用:
一、API话批商
严格来讲不算API话批商,真正一级API资源话批商是有自己的平台来开出API账号给到下游,我这里说的API“话批商”,指的是二手话批商。
使用场景:API线路商从多个一手API话批商接入资源,对接到OKCC的API资源管理平台,再将资源开给下游线路商。
二、API线路商
面向终端用户的API线路商,从多个上游接入API资源到OKCC的API资源管理平台,在API资源管理平台创建多个终端的企业账号,每个企业账号下面有对应的API资源。
三、终端用户
有业务系统,给自己的业务系统赋能通讯能力,且是API资源的能力。
扩展:
其实OKCC运营版的系统更加能满足企业的业务系统赋能需求,因为OKCC运营版不仅仅可以对接API资源,也可以对接SIP资源,并且还有很多呼叫中心业务功能接口可以对接。
那么问题来了,既然OKCC运营版能解决这些问题,那么API资源管理平台存在的意义是什么?
1、 API只能绑定一个IP,OKCC的并发上限1200并发,如果有两台OKCC服务器要用,那另外一台服务器就无法绑定这一个API账号,所以API资源管理平台是用来做资源分发的。
2、 操作方便,针对收量,API资源管理平台会更方便。
相关文章:

OKCC的API资源管理平台怎么用?
API资源管理平台,重点是“资源”管理平台,不是API接口管理平台。 天天讯通推出的API资源管理平台,类似昆石的VOS系统,区别是VOS是SIP资源管理系统,我们的API资源管理平台是API资源管理系统(AXB、AX、回拨AP…...

CentOS 7 安装python 3.7 需要必要的依赖。
在 CentOS 7 上部署 Python 3.7 可以通过源代码编译安装来实现。以下是大致的步骤: 安装必要的依赖: bashCopy Code sudo yum install gcc openssl-devel bzip2-devel libffi-devel 下载 Python 3.7 源代码并进行编译安装: bashCopy Code wg…...

美术馆设计方案优化布局与设施提升观众体验!
如今,美术馆不仅仅是作为展示艺术作品的平台,也是吸引公众参与和创造独特体验的数字艺术体验空间,因此许多传统美术馆在进行翻修改造时,都会更加注重用户体验,并在其中使用大量的多媒体互动,让参观者能够在…...

数据库基础原理
宏观 数据库的实现原理分为四个部分: 网络通信 网络协议 硬盘存储 内存分配 微观 硬盘存储 数据库是持久化的,而持久化如何实现的,我们不难想到磁盘可以持久化存储,所以数据库所有持久化的数据都是以文件形式存在磁盘中的…...
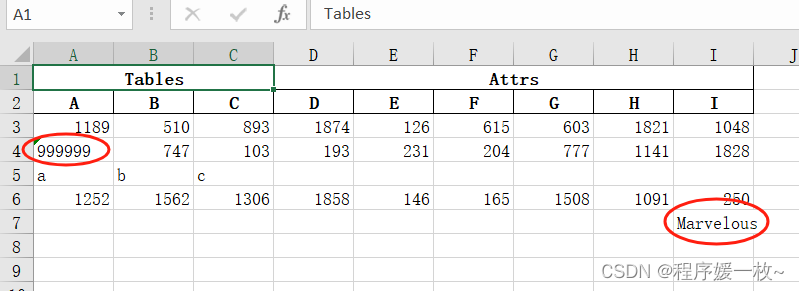
Pandas操作MultiIndex合并行列的Excel,写入读取以及写入多余行及Index列处理,插入行,修改某个单元格的值,多字段排序
Pandas操作MultiIndex合并行列的excel,写入读取以及写入多余行及Index列处理,多字段排序尽量保持原来的顺序 1. 效果图及问题2. 源码参考 今天是谁写Pandas的 复合索引MultiIndex,写的糊糊涂涂,晕晕乎乎。 是我呀… 记录下&#…...

工作总结5
1.taro框架使用map标签出现的错误 这个问题困扰很长时间,在频繁切换页面渲染的时候出现左边不显示,我理解的是变量没有到达map标签的属性上,那我就想是不是setState太慢了,然后又用了变量,本地缓存等,都没有…...
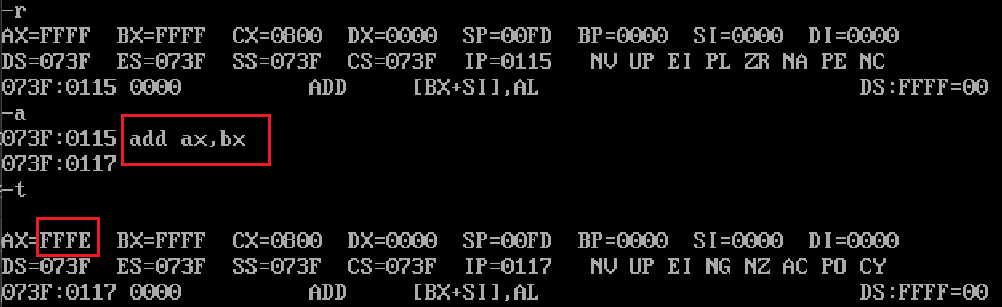
速通汇编(二)汇编mov、addsub指令
一,mov指令 mov指令的全称是move,从字面上去理解,作用是移动(比较确切的说是复制)数据,mov指令可以有以下几种形式 无论哪种形式,都是把右边的值移动到左边 mov 寄存器,数据&#…...

软考 - 系统架构设计师 - 构件组装技术
概念 构件组装是将库中的构件经修改后相互连接,或者将它们和当前开发项目中的软件元素进行连接,最终构成新的目标构件。 构件组装技术是基于构件的软件开发的核心技术,也是构件技术研究的重点和难点。构件组装的目的是利用现有的构件组装成新…...
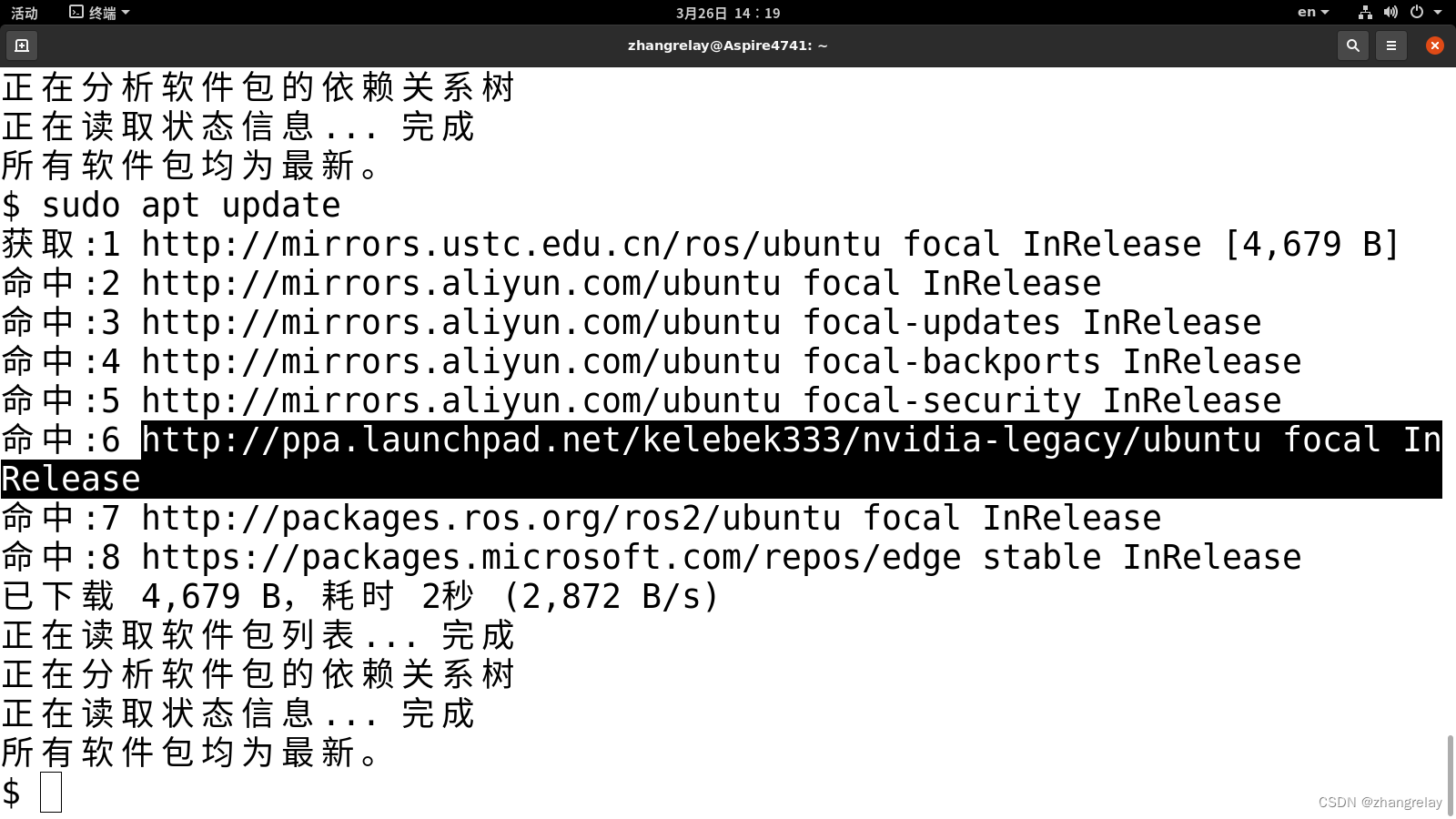
2010年之前电脑ubuntu安装nvidia驱动黑屏处理
装好驱动 仿真fps直接到60Hz 陈旧设备 都是非常老旧的电脑,没钱换新电脑,就这么穷…… 电脑详细配置: 冲动 想装显卡驱动提升一下性能,结果……黑了 黑习惯了也无所谓,几分钟就能解决,关键还是太穷&…...

类与对象中C++
加油!!! 文章目录 前言 一、类的6个默认成员函数 编辑 二、构造函数 1.概念 三、析构函数 1.概念 2.特性 四、拷贝构造函数 1.概念 2.特征 拷贝构造函数典型调用场景 五、赋值运算符重载 1.运算符重载 2.赋值运算符重载 赋值运算符重载格式…...

k8s 集群重启报错:The connection to the server 192.168.92.26:6443 was refused
[rootk8s-master ~]# kubectl get node The connection to the server 192.168.92.26:6443 was refused - did you specify the right host or port?查到是kubelet进程没有启动 [rootk8s-master ~]# systemctl status kubelet ● kubelet.service - kubelet: The Kubernetes …...

国内好用的chatGPT和AI绘图工具
分享一个比较好用的AI 分享一个比较好用的AI,只是需要开通会员,目前官网的价格是:298,开通之后可以使用chatgpt4、AI绘画、图片融合等等!不开通的话是可以免费使用15次的,下面是一些介绍图片!链…...

蚂蚁庄园3.31今日答案春季美食“雷竹笋”之所以得名是因为出笋与打雷有关吗?
蚂蚁庄园是一款爱心公益游戏,用户可以通过喂养小鸡,产生鸡蛋,并通过捐赠鸡蛋参与公益项目。用户每日完成答题就可以领取鸡饲料,使用鸡饲料喂鸡之后,会可以获得鸡蛋,可以通过鸡蛋来进行爱心捐赠。其中&#…...
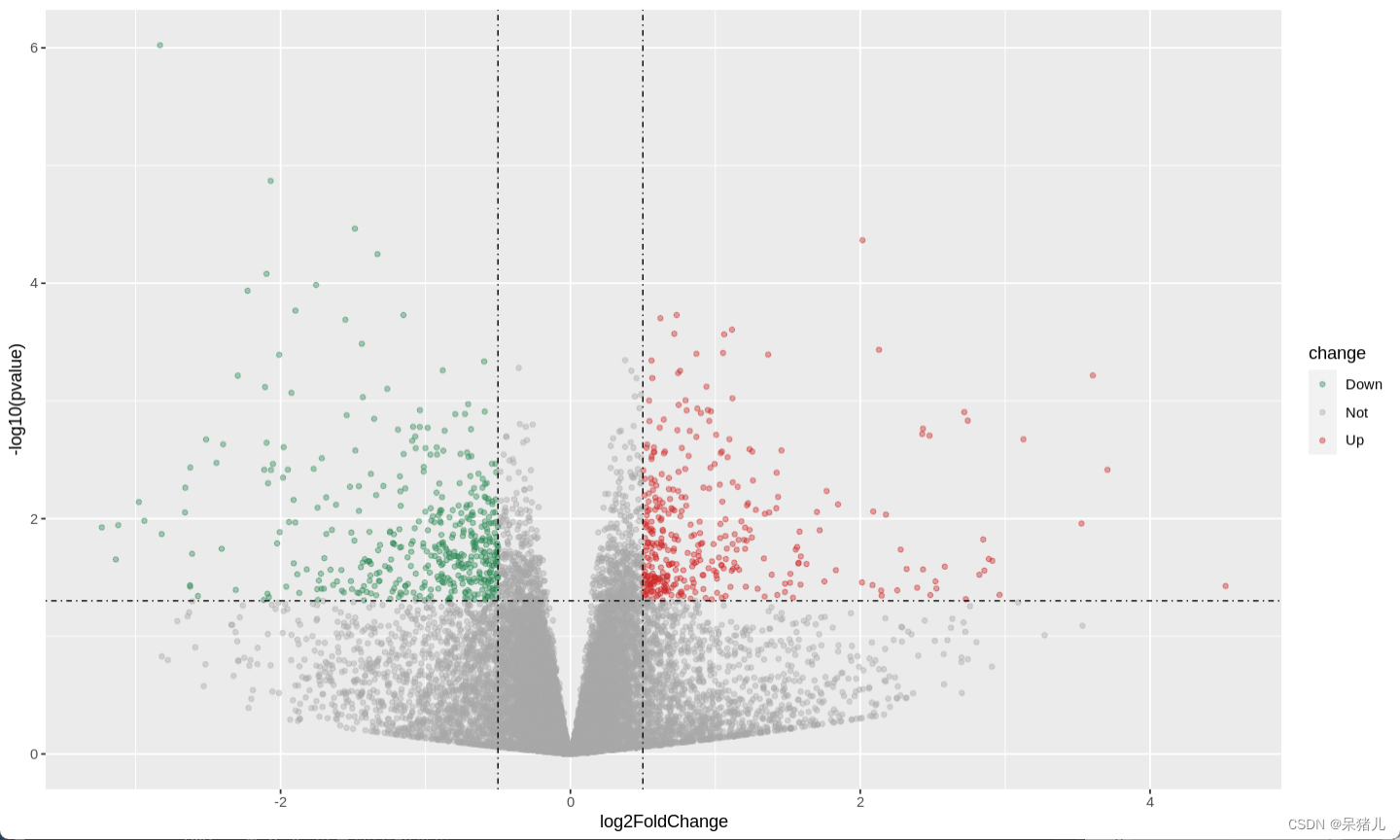
零基础入门转录组数据分析——绘制差异火山图
零基础入门转录组数据分析——绘制差异火山图 差异分析的火山图(Volcano Plot)在生物信息学数据分析中,特别是在基因表达差异分析中,是一个非常直观和有用的工具。 本教程将从导入的数据结构开始,一步步带大家在R中绘制好看的火山图,最后对火山图进行解读,确保读者理解…...

C++进阶,手把手带你学继承
🪐🪐🪐欢迎来到程序员餐厅💫💫💫 主厨:邪王真眼 主厨的主页:Chef‘s blog 所属专栏:c大冒险 总有光环在陨落,总有新星在闪烁 【本节目标】 1.继…...
、任务队列及底层原理)
Java自带的线程池及调用、ThreadPoolExecutor类(线程池的7大参数)、任务队列及底层原理
day32 线程池 引入 一个线程完成一项任务所需时间为: 创建线程时间 - Time1线程中执行任务的时间 - Time2销毁线程时间 - Time3 注意:优化在Time1,Time3(创建销毁线程费时间) 为什么需要线程池 线程池技术正是关注如何缩短或调整Time1和Tim…...

ThreadPool-线程池使用及原理
1. 线程池使用方式 示例代码: // 一池N线程 Executors.newFixedThreadPool(int) // 一个任务一个任务执行,一池一线程 Executors.newSingleThreadExecutorO // 线程池根据需求创建线程,可扩容,遇强则强 Executors.newCachedThre…...

高性能服务系列【十一】主题匹配
主题匹配核心算法就是字符串匹配,在字符串匹配基础上,会加入分段匹配需求,类似URL的点分式字符串。这个算法在几个场景中十分普遍。 1、应用层的路由寻址。比如反向代理中,根据请求中的URL,转发到对应的后台服务。 2…...
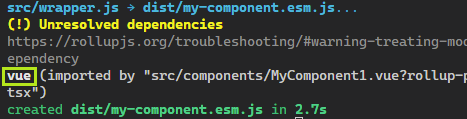
Vue 2 组件发布到 npm 的常见问题解决
按照 Vue 2 组件打包并发布到 npm 的方法配置项目后,项目在实际开发过程中,随着代码写法的多样性增加而遇到的各种打包问题,本文将予以逐一解决: 本文目录 同时导出多个组件 样式表 import 问题解决 Json 文件 import 问题解决…...

p2p原理
p2p原理 P2P (Peer-to-Peer) 是一种分布式计算和网络架构模型,它允许对等节点之间直接通信和共享资源,而无需通过集中的服务器。P2P 原理的核心概念是平等性(peer equality),即所有节点在网络中都具有相同的功能和能力…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...
