算法——动态规划:01背包
原始01背包见下面这篇文章:http://t.csdnimg.cn/a1kCL
01背包的变种:. - 力扣(LeetCode)
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
简化一下题目意思,即在一个数组中需要找若干个数,使这些数之和等于数组所有数据之和的一半。显然如果数组所有元素数据之和为奇数则必不可能找到。
与01背包问题类似,01背包问题的核心是在有限体积的背包内放入价值最大的物品;
dp[i][j]的定义为,从0到i这个范围内物品体积为j所能产生的最大价值。
状态变量:f[i][j]表示前i件物品放入容量为j的背包的最大价值
当前容量为j,我们要考虑第i件物品能否放入?是否放入?
如果当前背包容量j<v[i],不能放入,则f[i][j]=f[i-1][j]
如果当前背包容量j>=v[i],能放入但是要比较代价
2.1 如果第i件物品不放入背包,则f[i][j]=f[i-1][j]
2.2 如果第i件物品放入背包,则f[i][j]=f[i-1][j-v[i]]+w[i]

本题也类似,只是条件不是找到价值最大的,而是价值恰好等于目标值的若干个数。
dp[i][j]的定义为:从0到i范围内是否存在某几个数使这些数字之和恰好等于j;
状态转移方程为:如果0到i-1内存在和为j的数,则0到i之间也必然存在。
或者如果由当前目标j减去当前所在的数组数据nums[i],若0到i-1范围内存在和为j-nums[i]的数,则加上当前数据正好和为j,满足条件。
否则不存在。
核心代码为:
if(dp[i-1][j]||(nums[i]<=j&&dp[i-1][j-nums[i]]))
dp[i][j]=true;
需要注意的是,最开始初始化时,dp[0][i]需要找到一个i等于数组第一个数字numd[0],该dp[0][i]为true,其余均为false,表示0到0范围内不存在该数字。
初始化时dp[i][0]需要全部初始化为true,否则比如说第二个数字为2,2-2等于0,其实范围内出现了2,则一定满足条件。但是若dp[i][0]值为false反而会出错。
class Solution {
public:bool canPartition(vector<int>& nums) {int sum=0;for(int i=0;i<nums.size();i++)sum+=nums[i];if(sum%2==1)return false;vector<vector<bool>>dp(nums.size());int target=(sum>>1);for(int i=0;i<dp.size();i++){dp[i].resize(target+1);for(int j=0;j<=target;j++){dp[i][j]=false;}}for(int i=0;i<=target;i++){if(nums[0]==i){dp[0][i]=true;break;}}for(int i=0;i<nums.size();i++)dp[i][0]=true;for(int i=1;i<nums.size();i++){for(int j=1;j<=target;j++){if(dp[i-1][j]||(nums[i]<=j&&dp[i-1][j-nums[i]]))dp[i][j]=true;}}return dp[nums.size()-1][target];}
};相关文章:

算法——动态规划:01背包
原始01背包见下面这篇文章:http://t.csdnimg.cn/a1kCL 01背包的变种:. - 力扣(LeetCode) 给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。 简化一…...

写作类AI推荐(二)
本章要介绍的写作AI如下: 火山写作 主要功能: AI智能创作:告诉 AI 你想写什么,立即生成你理想中的文章AI智能改写:选中段落句子,可提升表达、修改语气、扩写、总结、缩写等文章内容优化:根据全文…...
(JAVA))
分寝室(20分)(JAVA)
目录 题目描述 输入格式: 输出格式: 输入样例 1: 输出样例 1: 输入样例 2: 输出样例 2: 题解: 题目描述 学校新建了宿舍楼,共有 n 间寝室。等待分配的学生中,有女…...

Spring 源码调试问题 ( List.of(“bin“, “build“, “out“); )
Spring 源码调试问题 文章目录 Spring 源码调试问题一、问题描述二、解决方案 一、问题描述 错误:springframework\buildSrc\src\main\java\org\springframework\build\CheckstyleConventions.java:68: 错误: 找不到符号 List<String> buildFolders List.of…...
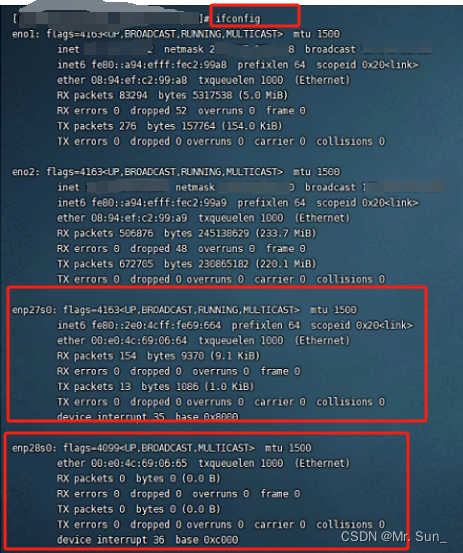
Centos7安装RTL8111网卡驱动
方法一: // 安装pciutils # yum install -y pciutils // 查看pci设备信息 # lspci | grep -i Ethernet 09:00.0 Ethernet controller: Realtek Semiconductor Co., Ltd. RTL8111/8168/8411 PCI Express Gigabit Ethernet Controller (rev 03) // 上面看到是Re…...

吉时利KEITHLEY2460数字源表
181/2461/8938产品概述: Keithley 2460 高电流源表源测量单元 (SMU) 将先进的触摸、测试和发明技术带到您的指尖。Keithley 2460 将创新的图形用户界面 (GUI) 与电容式触摸屏技术相结合,使测试变得直观并最大限度地缩短学习曲线,从而帮助工程…...
)
数据库原理(含思维导图)
数据库原理笔记,html与md笔记已上传 1.绪论 发展历程 记住数据怎么保存,谁保存数据,共享性如何,独立性如何 人工管理阶段 数据不保存应用程序管理数据数据不共享数据不具有独立性 文件系统阶段 数据可以长期保存文件系统管…...

数据结构(六)——图
六、图 6.1 图的基本概念 图的定义 图:图G由顶点集V和边集E组成,记为G (V, E),其中V(G)表示图G中顶点的有限非空集;E(G) 表示图G中顶点之间的关系(边)集合。若V {v1, v2, … , vn},则用|V|…...

Android-AR眼镜屏幕显示
Android-AR眼镜 前提:Android手持设备 需要具备DP高清口 1、创建Presentation(双屏异显) public class MyPresentation extends Presentation {private PreviewSingleBinding binding;private ScanActivity activity;public MyPresentatio…...

蓝桥集训之货币系统
蓝桥集训之货币系统 核心思想:背包 #include <iostream>#include <cstring>#include <algorithm>using namespace std;const int N 30,M 10010;typedef long long LL;LL f[M];int w[N];int n,m;int main(){cin>>n>>m;for(int i1;i&…...

基于微信小程序的校园服务平台设计与实现(程序+论文)
本文以校园服务平台为研究对象,首先分析了当前校园服务平台的研究现状,阐述了本系统设计的意义和背景,运用微信小程序开发工具和云开发技术,研究和设计了一个校园服务平台,以满足学生在校园生活中的多样化需求。通过引…...
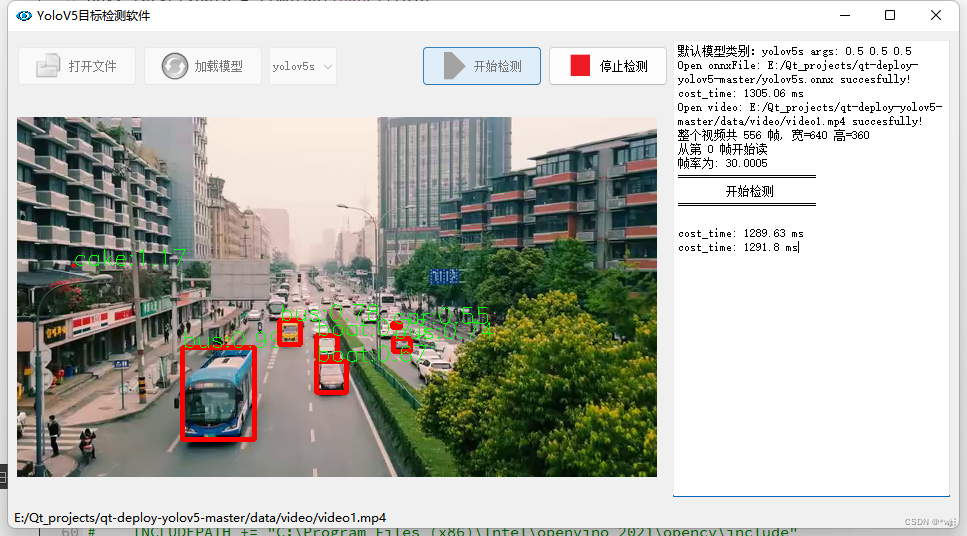
QT+Opencv+yolov5实现监测
功能说明:使用QTOpencvyolov5实现监测 仓库链接:https://gitee.com/wangyoujie11/qt_yolov5.git git本仓库到本地 一、环境配置 1.opencv配置 将OpenCV-MinGW-Build-OpenCV-4.5.2-x64文件夹放在自己的一个目录下,如我的路径: …...

【Python-Docx库】Word与Python的完美结合
【Python-Docx库】Word与Python的完美结合 今天给大家分享Python处理Word的第三方库:Python-Docx。 什么是Python-Docx? Python-Docx是用于创建和更新Microsoft Word(.docx)文件的Python库。 日常需要经常处理Word文档…...
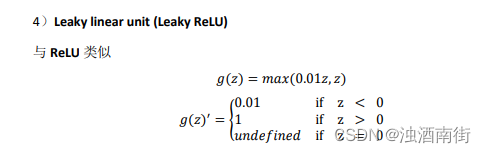
吴恩达深度学习笔记:浅层神经网络(Shallow neural networks)3.6-3.8
目录 第一门课:神经网络和深度学习 (Neural Networks and Deep Learning)第三周:浅层神经网络(Shallow neural networks)3.6 激活函数(Activation functions)3.7 为什么需要非线性激活函数?(why need a non…...

盘点最适合做剧场版的国漫,最后一部有望成为巅峰
最近《完美世界》动画官宣首部剧场版,主要讲述石昊和火灵儿的故事。这个消息一出,引发了很多漫迷的讨论,其实现在已经有好几部国漫做过剧场版,还有是观众一致希望未来会出剧场版的。那么究竟是哪些国漫呢,下面就一起来…...

Altium Designer许可需求分析
在电子设计的世界中,Altium Designer已成为设计师们的得力助手。然而,如何进行有效的许可需求分析,以确保软件的高效使用和企业的可持续发展?本文将带您了解如何进行Altium Designer的许可需求分析,让您在设计的道路上…...

[c++]类和对象常见题目详解
本专栏内容为:C学习专栏,分为初阶和进阶两部分。 通过本专栏的深入学习,你可以了解并掌握C。 💓博主csdn个人主页:小小unicorn ⏩专栏分类:C 🚚代码仓库:小小unicorn的代码仓库&…...
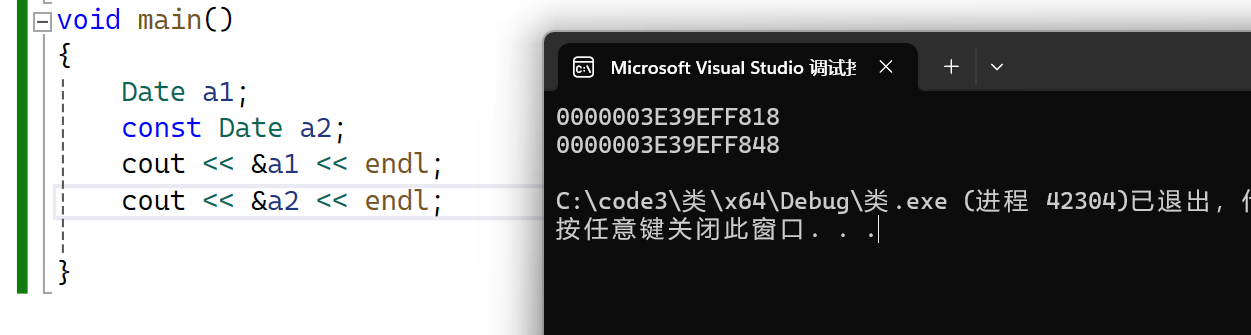
【c++】类和对象(五)赋值运算符重载
🔥个人主页:Quitecoder 🔥专栏:c笔记仓 朋友们大家好,本篇文章带大家认识赋值运算符重载,const成员,取地址及const取地址操作符重载等内容 目录 1.赋值运算符重载1.1运算符重载1.1.1特性&#…...
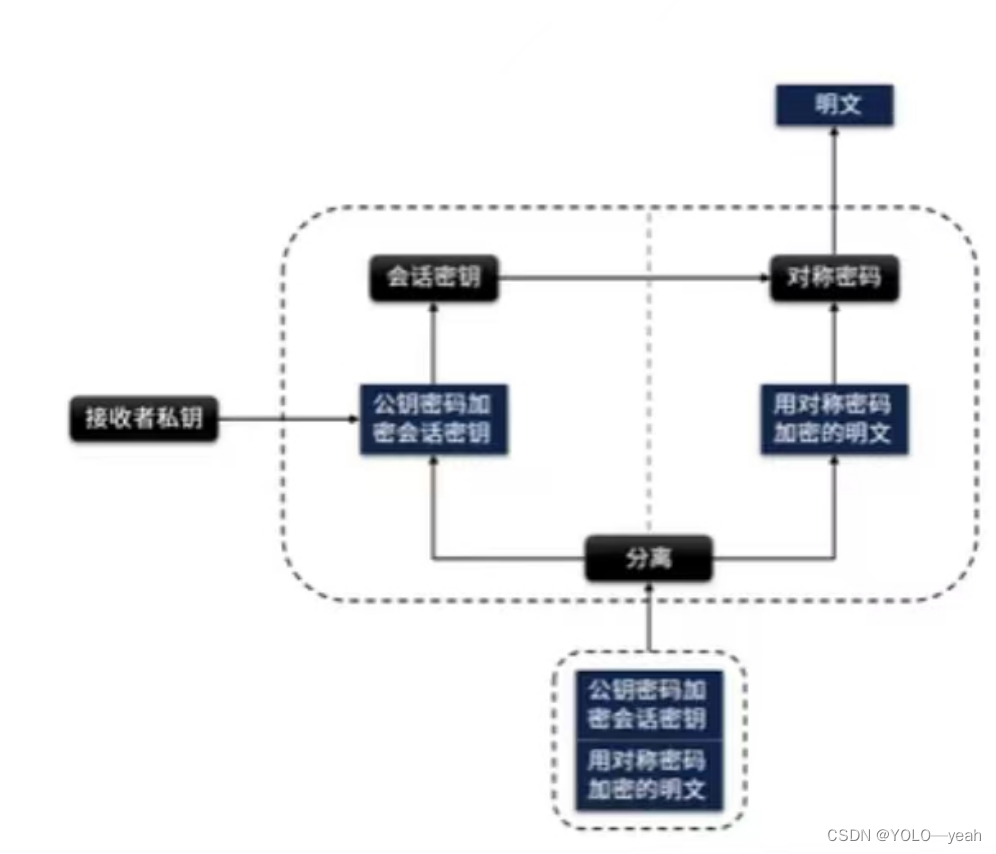
密码学基础-对称密码/公钥密码/混合密码系统 详解
密码学基础-对称密码/公钥密码 加解密说明1.加密解密必要因素加密安全性说明 什么是对称密码图示说明对称密码详解什么是DES?举例说明 什么是3DES什么是AES? 公钥密码什么是RSA? 对称密钥和公钥密码优缺点对比对称密码对称密码算法总结对称密码存在的问题? 公钥密码公钥密码…...
》)
《装饰器模式(极简c++)》
本文章属于专栏- 概述 - 《设计模式(极简c版)》-CSDN博客 模式说明: 方案: 装饰类和派生类同根,然后装饰类中放一个派生类,以在接口不动的情况下增加功能优点: 可以灵活地扩展对象功能…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...
