C#语言规范及特殊用法笔记
前言
记录在学习C#过程中遇到的知识点,会持续更新。
1. 常用数据类型结构的默认值
创建类的一个实例时,在执行构造函数之前,如果没给成员变量赋初始值,C#编译器将每一个成员变量初始化为默认值。虽然C#编译器为每个类型都设置了默认值,但作为面向对象的设计原则,还是需要对变量进行正确的初始化。
如果变量是方法的局部变量,编译器会认为在使用该变量之前,必须给它显示的设定一个值。否则会发生“使用了未赋值的局部变量”的错误。
对于其他情况,编译器会在创建变量时,把变量初始化为默认值。
常用数据类型及结构的默认值如下:
- 对于整型、浮点型,默认值为: 0或0.0
- 字符类型的默认值为: \x0000(空字符)
- 布尔类型的默认值为: false
- 引用类型的默认值为: null
- 枚举类型(enum)默认值是该枚举的第一个元素的默认值
- 结构体(struct)默认会将所有的值类型成员初始化为它们对应的默认值
- 数组会被初始化为引用类型的默认值:null
- 类类型(class)默认值为 : null
2. 可空类型和“??”、“?.”的用法说明
可空类型是指可以对非引用类型变量赋值“null”,语法为:
System.Nullable<int> a;
a = null";
// 以上两句等价于:int? a; // 语法糖
解决了 int a = null 会抛出错误的问题。当按照此方式定义时,变量a具有HasValue属性,该属性为bool类型,用来判别a是否有值,无值false有值true,有值时可使用Value属性:a.Value来调用其值。引用类型则不能如此操作(引用类型为null值时表示不存在引用对象)
??运算符被称为空接合运算符(null coalescing operator),是一个二元运算符,允许给可能等于null的表达式提供另一个值。如果第一个操作数不是null,该运算符就等于第一个操作数,否则,该运算符就等于第二个操作数。
a ?? b
// 上式等价于
a == null ? a : b
?.运算符通常称为空条件运算符,有助于避免繁杂的空值检查造成的代码歧义。
使用?.运算符,会把int? count设置为null,而不是抛出一个异常。
int? count = customer.orders?.Count();
// 结合??运算符和?.运算符,可以在结果为null时设置一个默认值
int? count = customer.orders?.Count() ?? 0;
未完待续……
参考资料
- 1: https://m.xp.cn/b.php/69938.html
- 2: https://blog.csdn.net/mingupup/article/details/134362284
相关文章:

C#语言规范及特殊用法笔记
前言 记录在学习C#过程中遇到的知识点,会持续更新。 1. 常用数据类型结构的默认值 创建类的一个实例时,在执行构造函数之前,如果没给成员变量赋初始值,C#编译器将每一个成员变量初始化为默认值。虽然C#编译器为每个类型都设置了…...
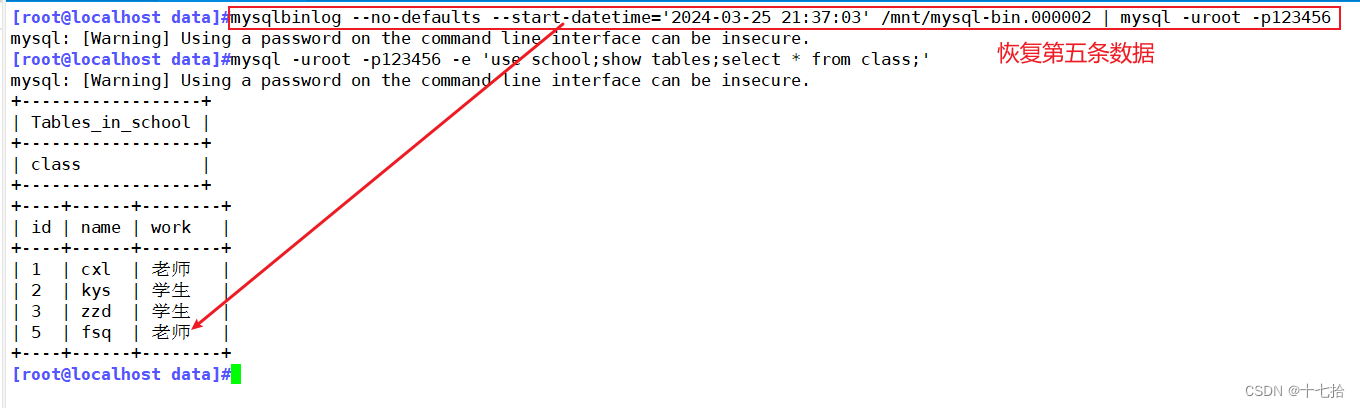
Mysql数据库:日志管理、备份与恢复
目录 前言 一、MySQL日志管理 1、存放日志和数据文件的目录 2、日志的分类 2.1 错误日志 2.2 通用查询日志 2.3 二进制日志 2.4 慢查询日志 2.5 中继日志 3、日志综合配置 4、查询日志是否开启 二、数据备份概述 1、数据备份的重要性 2、备份类型 2.1 从物理与…...
学习(八):K8S之常见部署方案)
kubernetes(K8S)学习(八):K8S之常见部署方案
K8S之常见部署方案 一、普通部署二、滚动更新(Rolling update)三、蓝绿部署(Blue/Green Deployment)四、灰度发布(金丝雀发布) 常见的部署方案参考博文:常见部署方案:普通部署、滚动…...

《AIGC重塑金融:AI大模型驱动的金融变革与实践》
🌈个人主页: Aileen_0v0 🔥热门专栏: 华为鸿蒙系统学习|计算机网络|数据结构与算法 💫个人格言:“没有罗马,那就自己创造罗马~” #mermaid-svg-oBSlqt4Vga1he7DL {font-family:"trebuchet ms",verdana,arial,sans-serif;font-siz…...
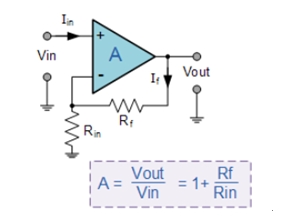
【详解】运算放大器工作原理及其在信号处理中的核心作用
什么是运算放大器 运算放大器(简称“运放”)是一种放大倍数非常高的电路单元。在实际电路中,它常常与反馈网络一起组成一定的功能模块。它是一种带有特殊耦合电路和反馈的放大器。输出信号可以是输入信号的加法、减法、微分和积分等数学运算…...
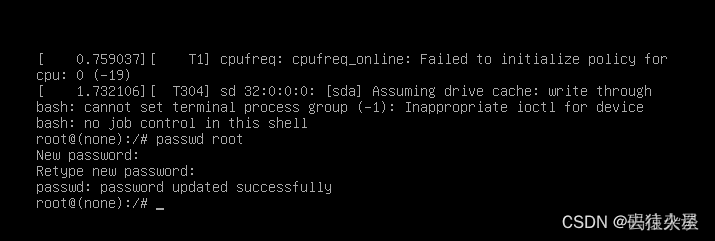
银河麒麟V10:sudo: /usr/bin/sudo 必须属于用户 ID 0(的用户)并且设置 setuid 位
一、引起原因: sudo chmod -R 777 bin 修改了/usr/bin/sudo的权限,引发后续问题。 二、现象: sudo执行命令报错: sudo: /usr/bin/sudo 必须属于用户 ID 0(的用户)并且设置 setuid 位 三、解决方法(知道root密码&…...

Android 多层级列表实现
方法一: Element.java : package com.chy.ydy.tools.treeutil; /*** TreeView 元素* */ public class Element {/** 文字内容 */private String contentText;/** 在tree中的层级 */private int level;/** 元素的id */private int id;/** 父元素的id */…...
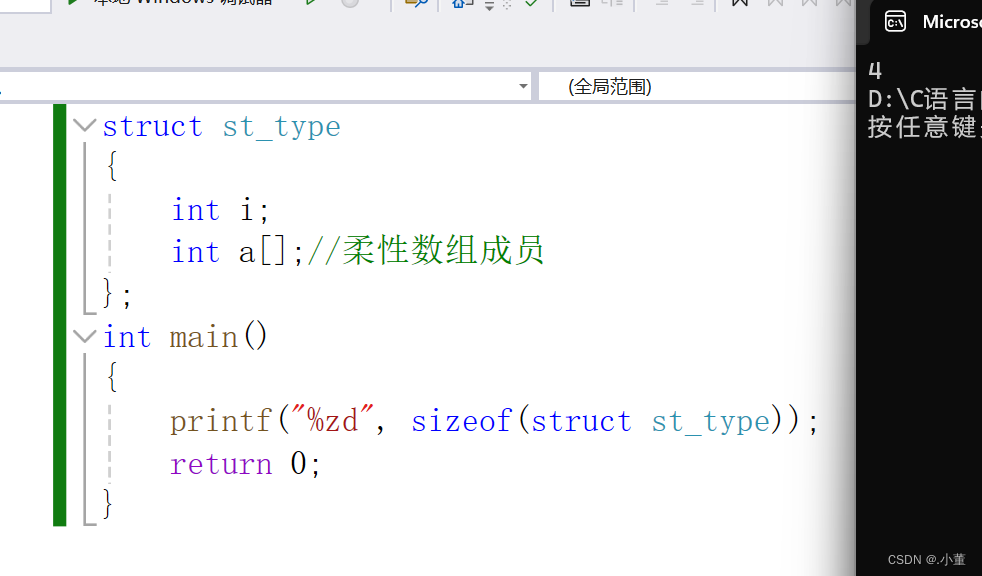
柔数组的介绍
柔数组简单介绍 这个词你可能没有听过但是他的确是存在的。 1.在c99中结构中的最后⼀个元素允许是未知⼤⼩的数组,这就叫做『柔性数组』成员 2这就代表了它存在与结构体中,很重要的一点是,他只能是结构体的最后的一个成员,这是…...

跳槽多次未成功,问题源自何处?
众所周知,2023年市场很难!看着企业们纷纷裁员,甚至连内推这个后门都走不通!哪怕有面试,都是屡屡碰壁,你想清楚问题出在哪了吗?😭“求职不得,夜不能寐;三更半夜…...

Linux 操作系统 022-串口/U盘/共享文件夹
Linux 操作系统 022-串口/U盘/共享文件夹 本节关键字:Linux、centos、串口、U盘、共享文件夹 本节相关指令:echo、cat、mkdir、mount 1、串口 #(1) 查看串口是否可用,可以对串口发送数据比如: $ echo helloworld >/dev/ttyS…...

java题目9:100匹马驮100担货,大马一匹驮3担,中马一匹驮2担,小马两匹驮1担。计算大中小马的数目(HorsesPackGoods9)
每日小语 正是他的意图损坏了他的悟性。——《充足理由律的四重根》 思考 有点鸡兔同笼的感觉嗷, //100匹马驮100担货,大马一匹驮3担,中马一匹驮2担,小马两匹驮1担。计算大中小马的数目(public class HorsesPackGoo…...
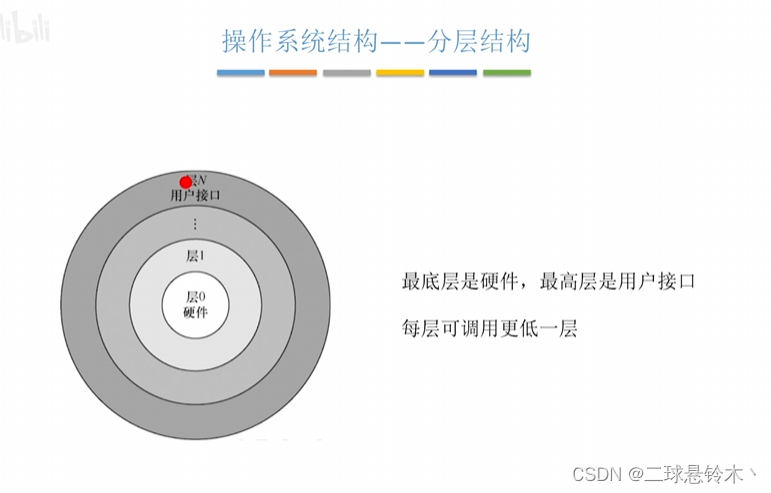
操作系统OS Chapter1
操作系统OS 一、概念和功能1.概念2.功能3.目标 二、特征1.并发2.共享3.虚拟4.异步 三、发展四、运行机制五、中断和异常1.中断的作用2.中断的类型3.中断机制的原理 六、系统调用七、操作系统结构八、操作系统引导九、虚拟机 一、概念和功能 1.概念 操作系统(OS&…...

UE4_Mouse_Interaction——拖拽物体的实现
鼠标拖拽物体,效果如下图: 1、新建PlayerController,更名字为MI_PlayerController,双击打开并设置参数: 2、新建GameMode,更名为MI_Gameinfo。参数如下设置: 3、新建材质,更名为BasicAsset02.参…...

Tomcat配置https
前言:本文内容为实操记录,仅供参考! 一、证书 CA证书申请下载不赘述了。 二、上传证书 进入tomcat根目录,conf同级目录下创建cert文件夹,并将证书两个文件上传到该文件夹; 三、编辑conf/server.xml文件 ① …...
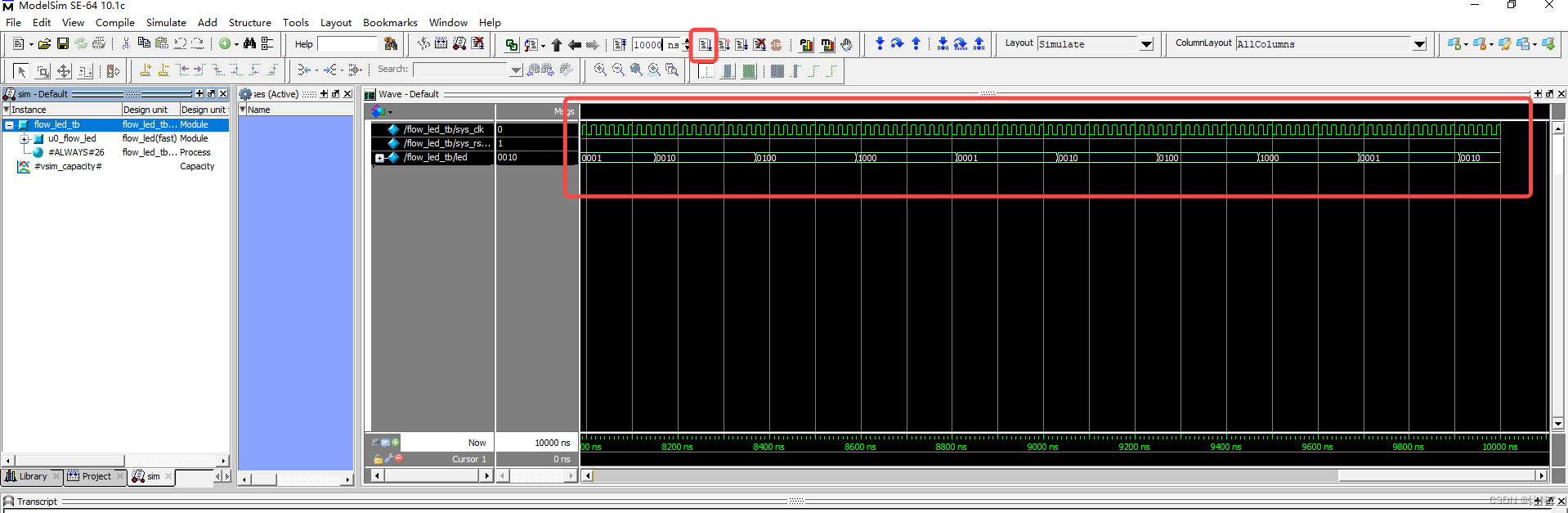
Modelsim手动仿真实例
目录 1. 软件链接 2. 为什么要使用Modelsim 3. Modelsim仿真工程由几部分组成? 4. 上手实例 4.1. 新建文件夹 4.2. 指定目录 4.3. 新建工程 4.4. 新建设计文件(Design Files) 4.5. 新建测试平台文件(Testbench Files&…...

AXI-Stream——草稿版
参考自哔站:FPGA IP之AXI4-Lite AXI4-Stream_哔哩哔哩_bilibili 信号 传输层级从小到大 包(----------transfer--transfer--------)------delay--------包(----------transfer--transfer--------) TKEEP和TSTRB共同决定了是哪种数据流...

【编码器应用】第一节-编码器从从原理到应用详解
概述: 本文内容为常用电机编码器概览,将为您重点介绍编码器大致分类,以及增量编码器与西门子设备的配置连接方式。 编码器简介 编码器是利用LED光源发出的透射光对码盘进行光电扫描,光电元件接收编码器轴旋转时产生的明暗交替变…...

瑞_23种设计模式_中介者模式
文章目录 1 中介者模式(Mediator Pattern)1.1 介绍1.2 概述1.3 中介者模式的结构1.4 中介者模式的优缺点1.5 中介者模式的使用场景 2 案例一2.1 需求2.2 代码实现 3 案例二3.1 需求3.2 代码实现 🙊 前言:本文章为瑞_系列专栏之《2…...

sqlite删除数据表
1.如何删除表 在SQLite中,删除表的SQL语句是DROP TABLE。如果你想要在Python中使用SQLite库(如sqlite3)来删除一个表,你可以按照以下步骤操作: 连接到SQLite数据库。创建一个cursor对象。执行DROP TABLE语句。提交事…...

Spring Boot简介及案例
文章目录 Spring Boot简介以下是一个简单的 Spring Boot Web 应用实例**步骤 1:创建 Spring Boot 项目****步骤 2:编写 RESTful 控制器****步骤 3:配置主类****步骤 4:运行并测试应用** Spring Boot简介 Spring Boot 是一个用于简…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...
实现跳一跳小游戏)
鸿蒙(HarmonyOS5)实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架,实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...

6️⃣Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙
Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙 一、前言:离区块链还有多远? 区块链听起来可能遥不可及,似乎是只有密码学专家和资深工程师才能涉足的领域。但事实上,构建一个区块链的核心并不复杂,尤其当你已经掌握了一门系统编程语言,比如 Go。 要真正理解区…...

Python 高级应用10:在python 大型项目中 FastAPI 和 Django 的相互配合
无论是python,或者java 的大型项目中,都会涉及到 自身平台微服务之间的相互调用,以及和第三发平台的 接口对接,那在python 中是怎么实现的呢? 在 Python Web 开发中,FastAPI 和 Django 是两个重要但定位不…...
