pygame通过重心坐标 用纹理填充三角形

texture_x = int(alpha * texture_image.get_width())
texture_y = int(beta * texture_image.get_height())为什么没有gama
2024/3/30 15:45:52
在使用重心坐标进行纹理映射时,通常是通过计算 alpha 和 beta 来确定纹理图片上的对应位置,而 gamma 通常是通过 alpha 和 beta 相互关系来计算的,因为重心坐标满足 alpha + beta + gamma = 1。因此,通常情况下不需要单独计算 gamma,因为它可以通过 alpha 和 beta 推导得到,从而减少了计算的复杂性和冗余。
import pygame
from pygame.locals import *
import sys
import mathpygame.init()width, height = 800, 600
screen = pygame.display.set_mode((width, height))vertices = [(160, 300, 1), (400, 40, 1), (600, 300, 1)]angle = 0
rotation_speed = 2 # 可根据需要调整旋转速度
c=pygame.time.Clock()
f=False
suofang=100
ax=0
ay=0
bx=0
by=0
cx=0
cy=0ci=0
zx=0
zy=0
zhongxina=0
zhongxinb=0
zhongxinc=0img=pygame.image.load("1.png").convert_alpha()
def draw_triangle(vertices):#points = [rotate_point(vertex, angle) for vertex in vertices]global ciglobal axglobal ayglobal bxglobal byglobal cxglobal cypoints = []new_vertices = []for x, y, z in vertices:new_x = x * math.cos(math.radians(angle)) - z * math.sin(math.radians(angle))new_z = x * math.sin(math.radians(angle)) + z * math.sin(math.radians(angle))new_vertices.append((new_x, y, new_z))(ax, ay, az), (bx, by, bz), (cx, cy, cz) = new_vertices#print(p,';;')# 绘制多边形#pygame.draw.polygon(screen, (200, 200, 200), transformed_points)#print(transformed_points)while True:screen.fill((255, 255, 255))#c.tick(7)for event in pygame.event.get():if event.type == QUIT:pygame.quit()sys.exit()keys = pygame.key.get_pressed()if keys[pygame.K_UP]:f = Trueif event.type == pygame.KEYUP:f = Falseif f==True:suofang=suofang-10draw_triangle(vertices)#angle += rotation_speed#print("....","ax",ax ,"ay",ay,"bx",bx,"by",by,"cx",cx,"cy",cy)for h in range(600):for w in range(600):zx = wzy = h# 重心坐标在求出中心后就不需要了,后面需要用这个坐标来判断屏幕中每个像素是否在三角形内#print(zx,zy)za1 = -(zx - bx) * (cy - by) + (zy - by) * (cx - bx)za2 = -(ax - bx) * (cy - by) + (ay - by) * (cx - bx)zhongxina = za1 / za2zb1 = -(zx - cx) * (ay - cy) + (zy - cy) * (ax - cx)zb2 = -(bx - cx) * (ay - cy) + (by - cy) * (ax - cx)zhongxinb = zb1 / zb2zhongxinc = 1 - zhongxina - zhongxinbif (0<zhongxina<1 and 0<zhongxinb<1 and 0<zhongxinc<1):#print(h,w)pygame.Surface.set_at(screen, (int(w), int(h)),(img.get_at((int(zhongxina*img.get_width()),int((zhongxinb*img.get_height()))))))#(img.get_at((int(i/10),int(gao/10)))))# zx =(ax + bx + cx) / 3# zy =(ay + by + cy) / 3# #重心坐标在求出中心后就不需要了,后面需要用这个坐标来判断屏幕中每个像素是否在三角形内## '''# x,y=500 abc三点不满足大于0小于1# -0.7076923076923077# 1.3282051282051281# 0.3794871794871797# 1.0## x,y=143 都满足大于0小于1,在三角形内# 0.94 0.04666666666666667 0.013333333333333384 1.0## x,y=300 都满足,在三角形内# 0.2153846153846154 0.6102564102564103 0.1743589743589743 1.0## x,y=0 不满足,不在三角形内# 1.6 -0.4666666666666667 -0.13333333333333341 0.9999999999999999## x=770,y=143 不满足 不在三角形内# -0.6676923076923077 -1.0251282051282051 2.692820512820513 1.0## x=230,y=190满足,在# 0.6205128205128205 0.147008547008547 0.23247863247863246 1.0# '''# za1=-(zx-bx)*(cy-by)+(zy-by)*(cx-bx)# za2=-(ax-bx)*(cy-by)+(ay-by)*(cx-bx)# zhongxina=za1/za2## zb1=-(zx-cx)*(ay-cy)+(zy-cy)*(ax-cx)# zb2=-(bx-cx)*(ay-cy)+(by-cy)*(ax-cx)# zhongxinb=zb1/zb2## zhongxinc=1-zhongxina-zhongxinb#print(zhongxina,zhongxinb,zhongxinc,zhongxina+zhongxinb+zhongxinc,"zx,",zx,"zy",zy)pygame.Surface.set_at(screen, (int(zx), int(zy)),(190, 90, 90))pygame.display.flip()
相关文章:

pygame通过重心坐标 用纹理填充三角形
texture_x int(alpha * texture_image.get_width()) texture_y int(beta * texture_image.get_height())为什么没有gama 2024/3/30 15:45:52 在使用重心坐标进行纹理映射时,通常是通过计算 alpha 和 beta 来确定纹理图片上的对应位置,而 gamma 通常是…...

Leetcode 611. 有效三角形的个数
给定一个包含非负整数的数组 nums ,返回其中可以组成三角形三条边的三元组个数。 示例 1: 输入: nums [2,2,3,4] 输出: 3 解释:有效的组合是: 2,3,4 (使用第一个 2) 2,3,4 (使用第二个 2) 2,2,3 示例 2: 输入: nums [4,2,3,4] 输出: 4 提示: 1 < nums.len…...
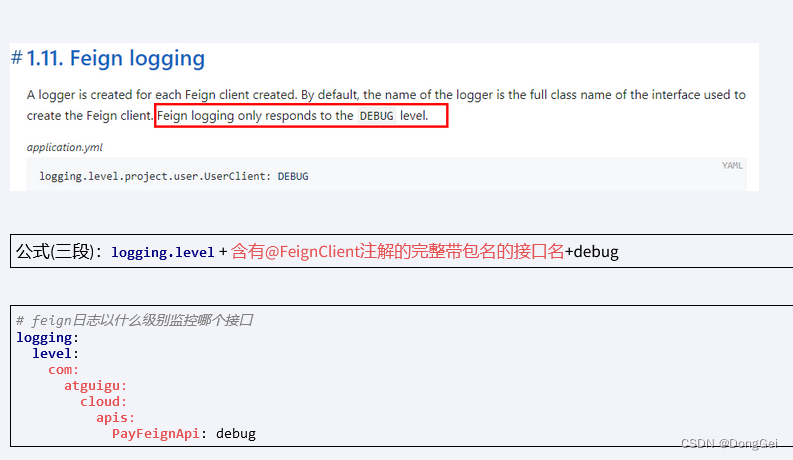
Openfeign
Openfeign 相关扩展 在 2020 以前的 SpringCloud 采用 Ribbon 作为负载均衡,但是 2020 年之后,SpringCloud 吧 Ribbon 移除了,而是使用自己编写的 LoadBalancer 替代. 因此,如果在没有加入 LoadBalancer 依赖的情况下,…...
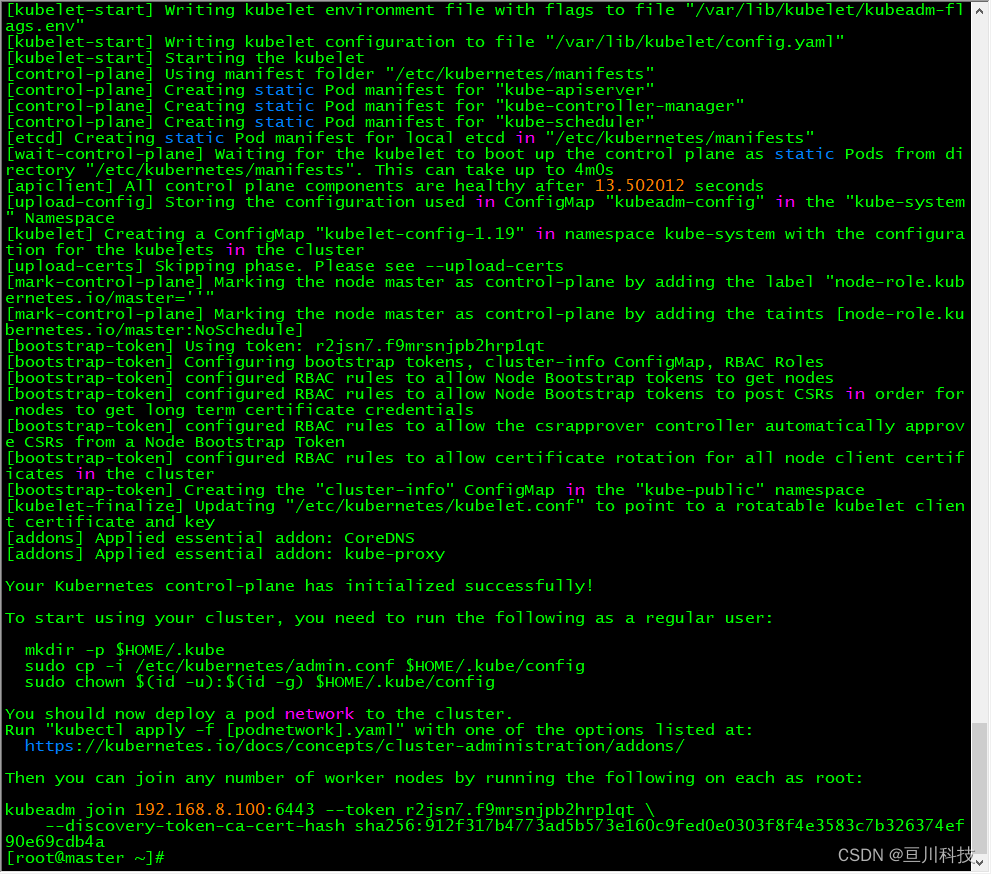
五、基于KubeAdm搭建多节点K8S集群
如需查阅上一步骤,请点击下面链接:四、戴尔R630本地服务器Linux Centos7.9系统安装docker-ce-20.10.10-3.el7版本-CSDN博客文章浏览阅读727次,点赞12次,收藏13次。1、准备工作3、Linux Centos7.9系统的iDRAC远程管理、网络设置、SecureCRT远程登录终端、企业级静态ip地址配…...
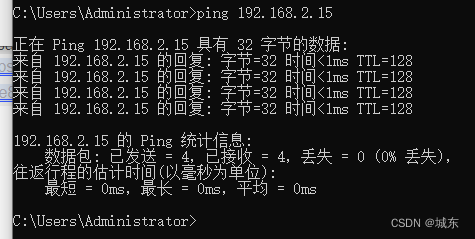
PC电脑技巧[笔记本通过网线访问设备CMW500]
笔记本局域网访问设备 现在我有一台CMW500,我要用笔记本去访问它,但是我发现没有路由器就是不能够访问,通过网线连接设备就是ping不通: 这里设置TCP/IPv4的IP地址如下,这时候就可以pin通了:...

【接口自动化测试框架】YAML管理接口框架配置的最佳实践
管理接口框架配置是构建强大的接口测试框架的关键一环。良好的配置管理可以提高测试效率、可维护性和可扩展性。在本文中,我们将重点介绍使用YAML(YAML Ain’t Markup Language)来管理接口框架配置的最佳实践,并通过实例演示其用法…...

【进程OI】基本文件操作的系统调用
文章目录 前言open参数flags参数mode writereadclose 前言 当用户想要向磁盘中的文件读写数据,就必须要得到操作系统的允许。同样,操作系统为了能让用户去对文件进行打开、读写、关闭等操作,向上提供了相应的系统调用的接口。C、JAVA、C等语…...

Ubuntu20.04 server系统部署安装(VMware上)和初始化配置
Ubuntu20.04 server部署安装(VMware上)和初始化配置 一、Ubuntu20.04 server系统部署安装上下键控制上下,可以选择配置的目标,回车表示确定,并进行下一步1.1镜像下载2.1 VMware上创建虚拟机2.2 选择语言,键…...
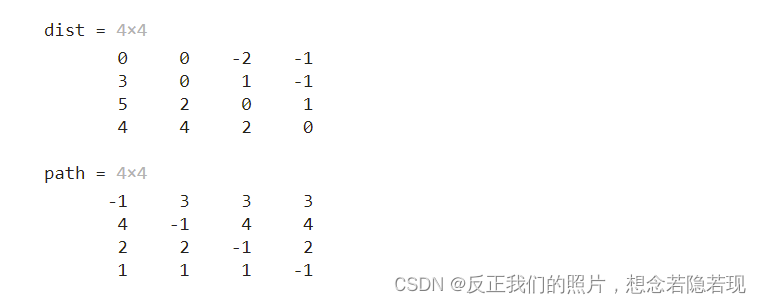
图论最短路径以及floyd算法的MATLAB实现
图论是数学的一个分支,起源于18世纪。1736年,数学家欧拉通过解决“哥尼斯堡七桥问题”,将问题抽象成点和线的关系,并通过理论分析得出结论,这个过程标志着图论的产生,欧拉也因此被称为“图论之父”。图论研…...
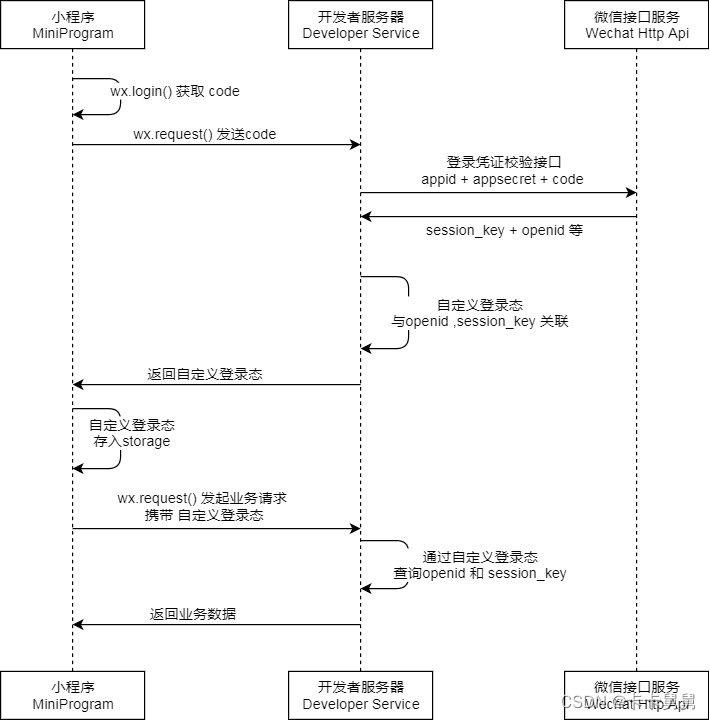
微信小程序 - 登录功能实现
一、认证流程 1. 小程序调用wx.login获取登录认证需要的code,并请求开发者服务器。 2. 开发者服务器根据code,appid, appsecret请求微信接口t获取 openid与session_key ,并生成自己的认证token,并返回给小程序。 3.小程序请求开…...

Python连接MySQL
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 一、整体思路二、连接流程三、表结构及代码实现 一、整体思路 二、连接流程 三、表结构及代码实现 代码块如下: import pymysqlcon pymysql.connect(h…...

水泊梁山108小酒坛之呼保义宋江
宋江【绰号呼保义、及时雨】字公明,是古典名著《水浒传》中的角色。原为山东郓城县押司,他和晁盖互通往来的事被阎婆惜发现,因此怒杀阎婆惜,逃回家隐藏。后前往清风寨投靠花荣,却被清风寨观灯时遭知寨刘高之妻陷害入狱…...

java.lang.ClassNotFoundException: javafx.application.Application
java8(jdk1.8)到java10(jdk10)中内含有JavaFx 在java11(jdk11)以及以后的版本中剥离出来需要开发者独立下载,另行导入download https://gluonhq.com/products/javafx/java --module-path $FX-P…...
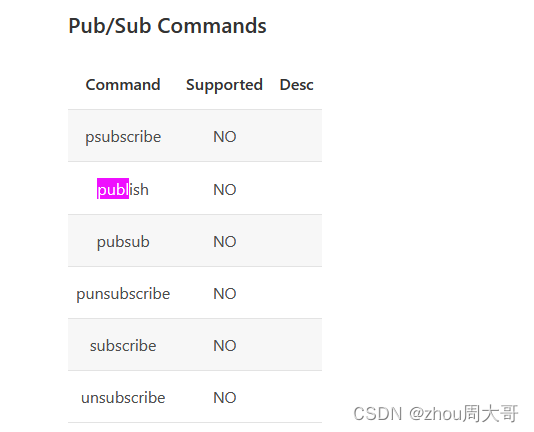
腾讯 tendis 替代 redis linux安装使用
下载地址 Tendis存储版 点击下载 linux 解压 tar -zxvf 安装包.tgz cd 解压安装包/scripts 启动 ./start.sh 停止 ./stop.sh 详细配置 修改 /scripts tendisplus.conf # tendisplus configuration for testing # 绑定本机IIP bind 192.168.31.112 port 51002 #设…...

k8s调优--来自gpt
Kubernetes(K8s)性能调优是一个涉及多个方面的过程,旨在提高集群的效率和响应速度。这包括对节点、Pod、服务、网络和存储等多个层面进行调优。下面我将概述一些常见的Kubernetes性能调优方法: 节点级别的调优: 1.资源分配&…...
HTML5+CSS3小实例:旋转中的视差效果
实例:旋转中的视差效果 技术栈:HTML+CSS 效果: 源码: 【HTML】 <!DOCTYPE html> <html lang="zh-CN"> <head><meta charset="UTF-8"><meta name="viewport" content="width=device-width, initial-scal…...

3-zookeeper之ZAB协议
Zookeeper ZAB协议 概述 ZAB(Zookeeper Automic Broadcast)是一套专门为Zookeeper设计的用于进行原子广播和崩溃恢复的协议ZAB协议主要包含了两个功能 原子广播:保证数据一致性崩溃恢复:保证集群的高可用 ZAB协议本身是基于2PC算法来进行的设计&#…...

如何为企业策划一场XR虚拟直播?
活动年年办,都是老一套,想玩点新花样? 预算有限,但还是想把活动办的逼格高一点? 想通过活动,让更多的人知道自己企业的品牌? 随着AIGC技术的不断演变,企业活动的形式和内容也在不…...

6.3物联网RK3399项目开发实录-驱动开发之I2C 使用(wulianjishu666)
物联网开发源码案例集: 链接:https://pan.baidu.com/s/1kfPDpYZpm_G0GBLAup3KTQ?pwdvgvv I2C 使用 简介 AIO-3399J 开发板上有 9 个片上 I2C 控制器,各个 I2C 的使用情况如下表: 本文主要描述如何在该开发板上配置 I2C。 配置…...

HarmonyOS实战开发-如何构建多种样式弹窗
介绍 本篇Codelab将介绍如何使用弹窗功能,实现四种类型弹窗。分别是:警告弹窗、自定义弹窗、日期滑动选择器弹窗、文本滑动选择器弹窗。需要完成以下功能: 点击左上角返回按钮展示警告弹窗。点击出生日期展示日期滑动选择器弹窗。点击性别展…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...

Unity VR/MR开发-VR开发与传统3D开发的差异
视频讲解链接:【XR马斯维】VR/MR开发与传统3D开发的差异【UnityVR/MR开发教程--入门】_哔哩哔哩_bilibili...

接口 RESTful 中的超媒体:REST 架构的灵魂驱动
在 RESTful 架构中,** 超媒体(Hypermedia)** 是一个核心概念,它体现了 REST 的 “表述性状态转移(Representational State Transfer)” 的本质,也是区分 “真 RESTful API” 与 “伪 RESTful AP…...
