(75)爬楼梯
文章目录
- 1. 每日一言
- 2. 题目
- 2.1 解题思路
- 2.1.1 递归
- 2.1.2 记忆化搜索
- 2.1.3 动态规划
- 2.1.4 动态规划空间优化
- 2.2 代码
- 2.2.1 递归
- 2.2.2 记忆化搜索
- 2.2.3 动态规划
- 2.2.4 动态规划空间优化
- 3. 结语
1. 每日一言
Happy life lies in a peaceful mind.
幸福的生活存在于心绪的宁静之中。
2. 题目
题目链接:爬楼梯
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
-
示例 1:
输入:n = 2
输出:2
解释:有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶 -
示例 2:
输入:n = 3
输出:3
解释:有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶
提示:
1 <= n <= 45
2.1 解题思路
2.1.1 递归
-
首先,函数判断如果 n 小于等于 2,则直接返回 n。因为在楼梯阶数小于等于 2 的情况下,只有一种方式爬到顶部,即分别走一步或者直接跨两步。
-
对于大于 2 的情况,函数采用递归的方式进行计算。爬到第 n 阶楼梯的方式数量等于爬到第 n-1 阶和第 n-2 阶的方式数量之和。这是因为爬到第 n 阶楼梯只有两种方式,一种是从第 n-1 阶再爬一阶,另一种是从第 n-2 阶再跨两阶。
-
最后,将计算得到的方式数量 sum 返回。
2.1.2 记忆化搜索
- 首先,定义一个全局数组 men,大小为 46(因为题目中规定楼梯数不超过 45)。这个数组用来保存已经计算过的楼梯阶数对应的爬楼梯方式数量,避免重复计算。
- 接下来定义一个递归函数 climb(int n),用来计算爬到第 n 阶楼梯的方式数量。如果 n 小于等于 2,则直接返回 n,表示只有一种或两种方式爬到顶部。
- 如果 men[n] 不为 -1,说明之前已经计算过爬到第 n 阶楼梯的方式数量,直接返回 men[n]。
- 如果 men[n] 为 -1,说明还没有计算过爬到第 n 阶楼梯的方式数量,此时调用递归函数 climb(n-1) + climb(n-2) 来计算,并将结果保存在 men[n] 中,然后返回该结果。
- 最后,在 climbStairs 函数中,将 men 数组初始化为 -1,并调用 climb 函数来求解爬楼梯问题。
2.1.3 动态规划
- 首先,定义一个长度为 46 的整型数组 climb,用来存储爬到每个楼梯阶数的方式数量。数组初始化为 [1, 2],表示爬到第一阶和第二阶楼梯的方式数量分别为 1 和 2。
- 接下来,使用一个循环从第三阶楼梯开始计算爬楼梯的方式数量。对于第 i 阶楼梯,爬到这一阶的方式数量等于爬到第 i-1 阶和第 i-2 阶的方式数量之和,因为只有两种方式可以到达第 i 阶楼梯,要么是从第 i-1 阶跨一步,要么是从第 i-2 阶跨两步。
- 最后,返回数组 climb 中第 n-1 个元素,即爬到第 n 阶楼梯的方式数量。
2.1.4 动态规划空间优化
- 如果输入的楼梯阶数 n 小于等于 2,那么直接返回 n,因为在这种情况下,只有一阶或者两阶楼梯,爬到顶部的方式数量分别为 1 和 2。
- 对于大于 2 的情况,定义三个变量 a、b 和 c,分别表示爬到第 n-2、第 n-1 和第 n 阶楼梯的方式数量。初始时,a 被赋值为 1(表示爬到第一阶楼梯的方式数量),b 被赋值为 2(表示爬到第二阶楼梯的方式数量)。
- 使用一个循环来计算爬到第 n 阶楼梯的方式数量。循环从第 3 阶楼梯开始,依次计算爬到每一阶楼梯的方式数量,直到计算到第 n 阶为止。
- 在循环中,更新 c 的值为 a + b,然后将 b 的值赋给 a,将 c 的值赋给 b,以便继续下一轮循环。
- 循环结束后,c 中存储的就是爬到第 n 阶楼梯的方式数量。
- 最后,返回 c。
2.2 代码
2.2.1 递归
int climbStairs(int n) {if(2 >= n) {return n;}int sum = 0;sum = climbStairs(n-1) + climbStairs(n-2);return sum;
}
2.2.2 记忆化搜索
int men[46];
int climb(int n) {if(n <= 2) {return n;}if(men[n] != -1) {return men[n];}return men[n] = climb(n-1) + climb(n-2);;
}
int climbStairs(int n) {for(int i = 0; i < 46; i++) {men[i] = -1;}return climb(n);
}
2.2.3 动态规划
int climbStairs(int n) {int climb[46];climb[0] = 1;climb[1] = 2;for(int i = 2; i < n; i++) {climb[i] = climb[i-1] + climb[i-2];}return climb[n-1];
}
2.2.4 动态规划空间优化
int climbStairs(int n) {if(n <= 2) {return n;} else {int a = 1;int b = 2;int c = 0;while(n > 2) {c = a + b;a = b;b = c;--n;}return c;}
}
3. 结语
请给自己些耐心,不要急于求成。
山外青山楼外楼,莫把百尺当尽头。
保持空杯心态加油努力吧!
都看到这里啦!真棒(*^▽^*)
可以给作者一个免费的赞赞吗,这将会鼓励我继续创作,谢谢大家
编程小白写作,如有纰漏或错误,欢迎指正
相关文章:
爬楼梯)
(75)爬楼梯
文章目录 1. 每日一言2. 题目2.1 解题思路2.1.1 递归2.1.2 记忆化搜索2.1.3 动态规划2.1.4 动态规划空间优化 2.2 代码2.2.1 递归2.2.2 记忆化搜索2.2.3 动态规划2.2.4 动态规划空间优化 3. 结语 1. 每日一言 Happy life lies in a peaceful mind. 幸福的生活存在于心绪的宁静…...
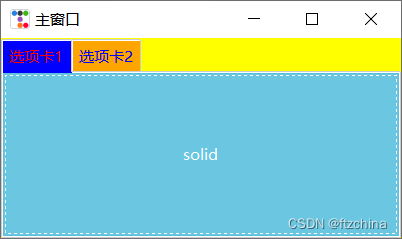
ttkbootstrap界面美化系列之Notebook(四)
在简单的界面设计中,Notebook也是常用的组件之一,Notebook组件的引入可以根据标签来切换不同的界面。使得界面更有层次感,不必都挤在一个界面上。在tkinter中就有Notebook组件,在ttkbootstrap中,同样也对Notebook进行了…...

MySQL8存储过程整合springboot
注意:调用使用mybatis-plus3形式调用,可能会有些区别 1. 创建存储过程 -- -- 生成员工工号的存储过程 DELIMITER $$ CREATE PROCEDURE generate_employee_number(OUT employeeNumber VARCHAR(20)) -- 解释 out 一个返回值 BEGINDECLARE prefix VARCHAR…...

Acwing 1238.日志统计 双指针
小明维护着一个程序员论坛。现在他收集了一份”点赞”日志,日志共有 N� 行。 其中每一行的格式是: ts id 表示在 ts 时刻编号 id 的帖子收到一个”赞”。 现在小明想统计有哪些帖子曾经是”热帖”。 如果一个帖子曾在任意一个长度为 D 的…...

Matlab-R2022b-安装文件分享
一、MATLAB主要特点和功能 MATLAB是一款强大的科学计算软件,专门用于算法开发、数据分析、数值计算以及科学数据可视化。 以下是一些MATLAB的主要特点和功能: 1.矩阵运算: MATLAB的名字来源于"Matrix Laboratory"(矩阵实验室&…...

Flutter开发之objectbox
Flutter开发之objectbox 在之前进行iOS开发的时候使用WCDB去进行管理数据库很方便,它支持ORM(Object-Relational Mapping,对象关系映射),用于实现面向对象编程语言里不同类型系统的数据之间的转换。 那么在Flutter开发…...
)
AI Drug Discovery Design(学习路线)
AIDD,即AI Drug Discovery & Design,是近年来非常火热的技术应用,已经介入到新药设计到研发的大部分环节当中,为新药发现与开发带来了极大的助力。其学习路线涉及多个学科和领域的知识。以下是一个可能的AIDD学习路线…...

【软考】设计模式之状态模式
目录 1. 说明2. 应用场景3. 结构图4. 构成5. 优缺点5.1 优点5.2 缺点 6. java示例6.1 非状态模式6.1.1 问题分析6.1.2 接口类6.1.2 实现类6.1.3 客户端6.1.4 结果截图 6.2 状态模式6.2.1 抽象状态类6.2.2 状态类6.2.3 上下文类6.2.4 上下文类 1. 说明 1.允许一个对象在其内部状…...

MNN介绍、安装与编译:移动端深度学习推理引擎
MNN介绍、安装与编译:移动端深度学习推理引擎 引言第一部分:MNN简介第二部分:MNN的安装第三部分:MNN的编译结语 引言 大家好,这里是程序猿代码之路。在移动设备上实现高效的深度学习模型推理一直是人工智能领域的一个挑…...
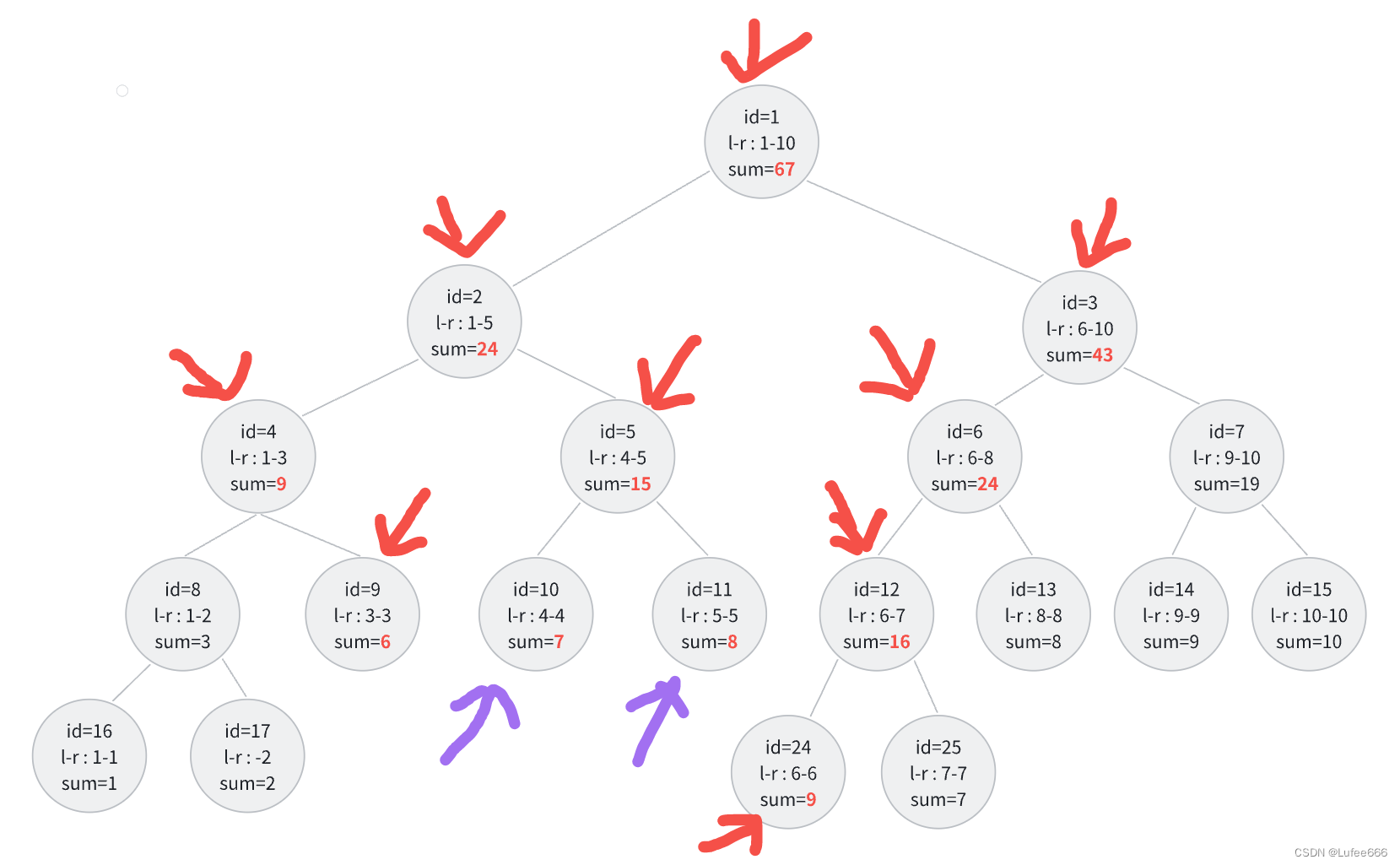
A Simple Problem with Integers(线段树)
目录 描述 输入 输出 样例输入 样例输出 思路 建树 第一次错误解法(正确解法在下面,可跳过这一步) 正确解法 code 描述 You have N integers, A1, A2, ... , AN. You need to deal with two kinds of operations. One type of …...
用例简介)
单元测试(UT)用例简介
单元测试(Unit Testing, UT)用例是一系列预先设计好的、针对软件最小可测试单元的测试场景。每一个单元测试用例都是为了验证一个独立代码单元(如函数、方法、类)的行为是否符合预期。这些用例通常包含以下几个关键组成部分&#…...

Java通过反射机制获取类对象下的属性值
目录 以类USER为例: 使用Java的反射机制获取Column的name为“user_name”的类属性值 以类USER为例: import lombok.Data; import javax.persistence.*; import java.io.Serializable;Data Table(name "user_info") public class User imple…...

IDEA插件开发-File -> New->Project中添加一个myOptions
写一个IDEA插件,在IDEA的File -> New -> Project 中添加一个选项myOptions ,点击myOptions 后弹出一个提示对话框:被点击了 为了在IntelliJ IDEA中创建一个插件,您需要遵循一系列的步骤来开发和集成您的功能。下面是一个简化的指南&am…...
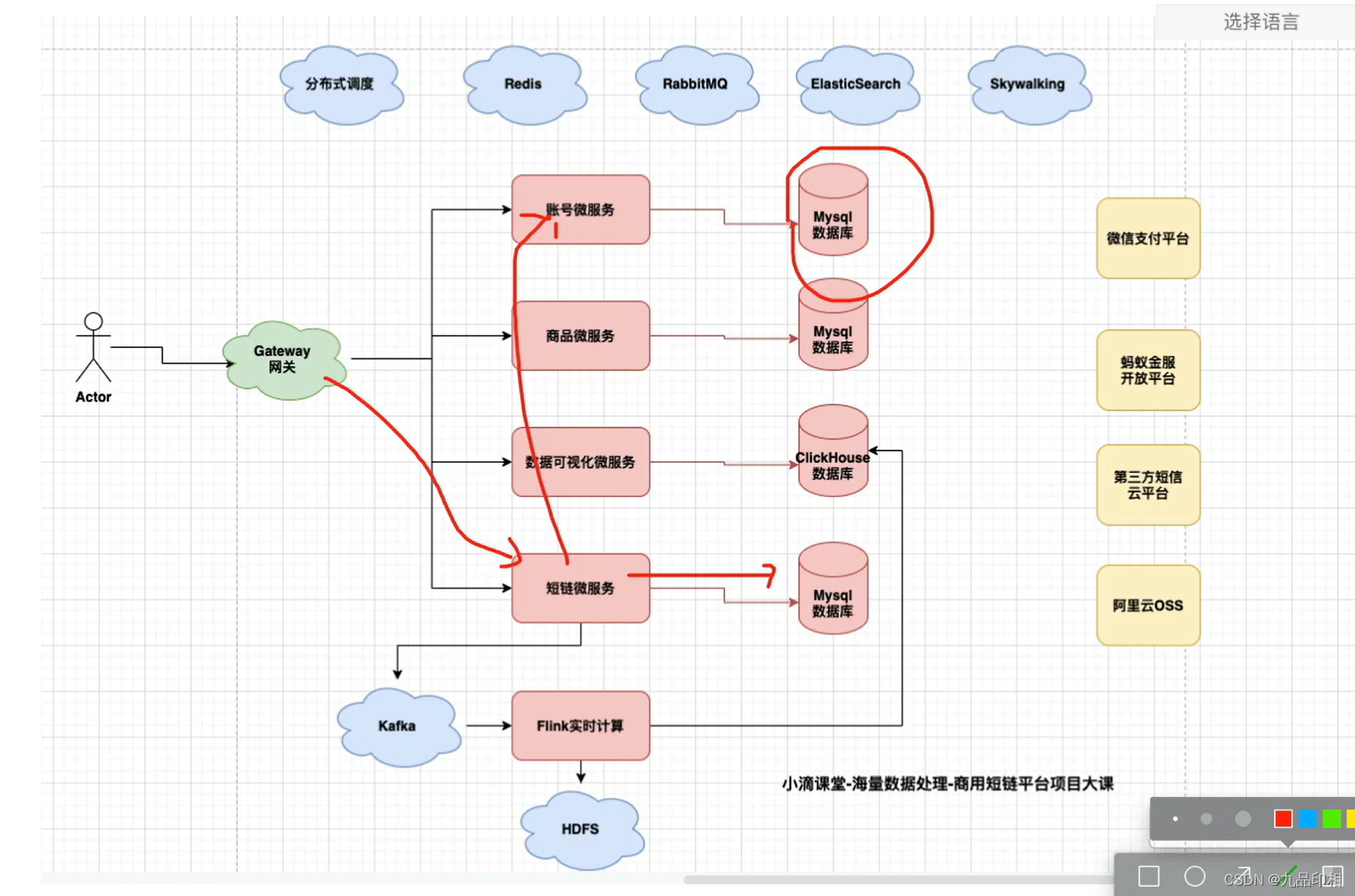
海量数据处理项目-账号微服务和流量包数据库表+索引规范(下)
海量数据处理项目-账号微服务和流量包数据库表索引规范(下) 第2集 账号微服务和流量包数据库表索引规范讲解《下》 简介:账号微服务和流量包数据库表索引规范讲解 账号和流量包的关系:一对多traffic流量包表思考点 海量数据下每…...
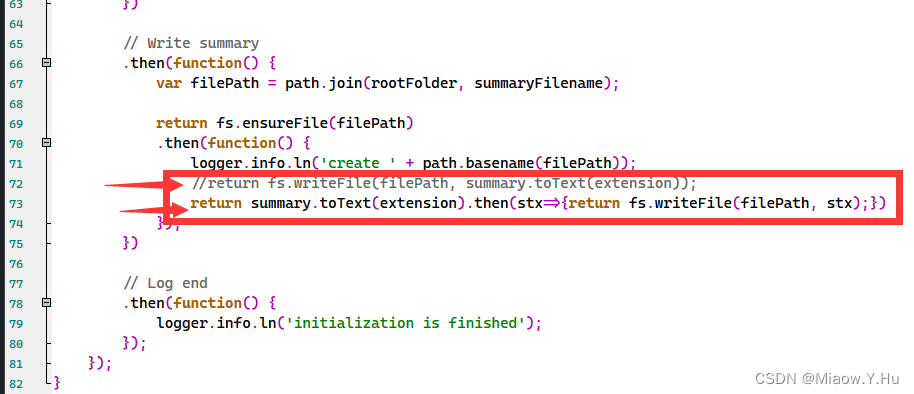
Nodejs 16与 gitbook搭建属于你自己的书本网站-第一篇
最近想重新搭建一个网站来存放自己的相关知识点,并向网络公开,有个hexo博客其实也不错的,但是总感觉hexo很多花里胡哨的玩意,导致挂载的博客异常卡,这样反而不利于我自己回顾博客了,于是我就开始钻研这个鬼…...

服务器被CC攻击之后怎么办?
1.取消域名绑定取消域名绑定后Web服务器的CPU能够马上恢复正常状态,通过IP进行访问连接一切正常。但是不足之处也很明显,取消或者更改域名对于别人的访问带来了不变,另外,对于针对IP的CC攻击它是无效的,就算更换域名攻…...

pygame通过重心坐标 用纹理填充三角形
texture_x int(alpha * texture_image.get_width()) texture_y int(beta * texture_image.get_height())为什么没有gama 2024/3/30 15:45:52 在使用重心坐标进行纹理映射时,通常是通过计算 alpha 和 beta 来确定纹理图片上的对应位置,而 gamma 通常是…...

Leetcode 611. 有效三角形的个数
给定一个包含非负整数的数组 nums ,返回其中可以组成三角形三条边的三元组个数。 示例 1: 输入: nums [2,2,3,4] 输出: 3 解释:有效的组合是: 2,3,4 (使用第一个 2) 2,3,4 (使用第二个 2) 2,2,3 示例 2: 输入: nums [4,2,3,4] 输出: 4 提示: 1 < nums.len…...
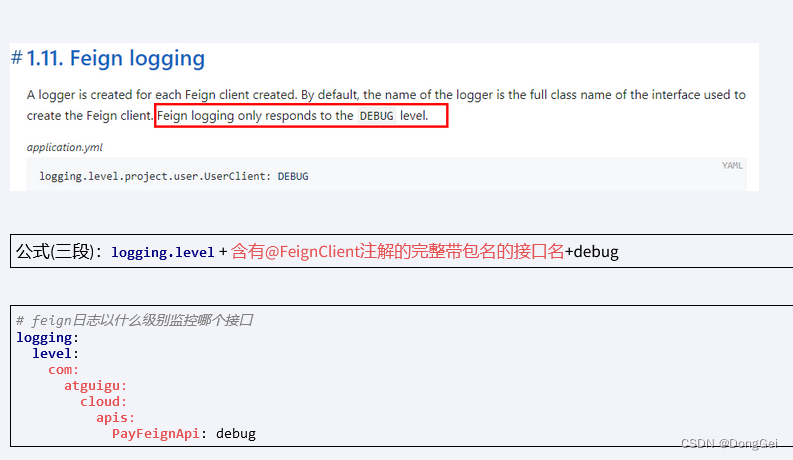
Openfeign
Openfeign 相关扩展 在 2020 以前的 SpringCloud 采用 Ribbon 作为负载均衡,但是 2020 年之后,SpringCloud 吧 Ribbon 移除了,而是使用自己编写的 LoadBalancer 替代. 因此,如果在没有加入 LoadBalancer 依赖的情况下,…...
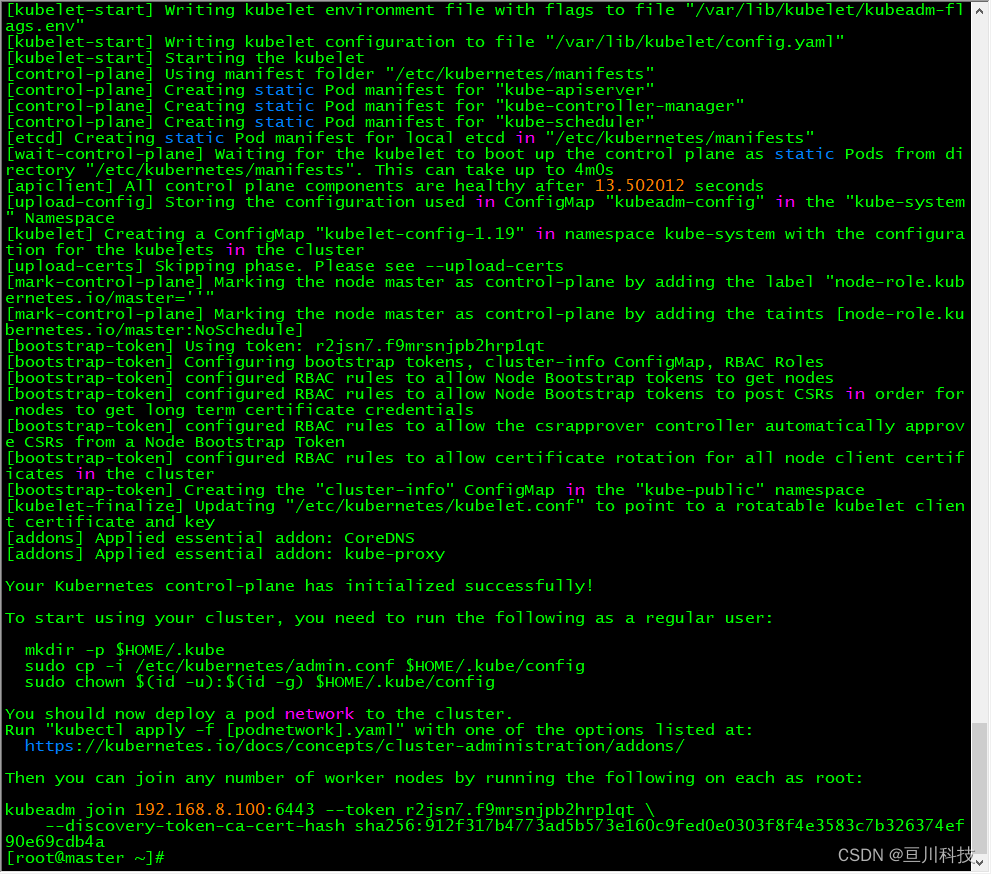
五、基于KubeAdm搭建多节点K8S集群
如需查阅上一步骤,请点击下面链接:四、戴尔R630本地服务器Linux Centos7.9系统安装docker-ce-20.10.10-3.el7版本-CSDN博客文章浏览阅读727次,点赞12次,收藏13次。1、准备工作3、Linux Centos7.9系统的iDRAC远程管理、网络设置、SecureCRT远程登录终端、企业级静态ip地址配…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...

Python 高效图像帧提取与视频编码:实战指南
Python 高效图像帧提取与视频编码:实战指南 在音视频处理领域,图像帧提取与视频编码是基础但极具挑战性的任务。Python 结合强大的第三方库(如 OpenCV、FFmpeg、PyAV),可以高效处理视频流,实现快速帧提取、压缩编码等关键功能。本文将深入介绍如何优化这些流程,提高处理…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...

保姆级【快数学会Android端“动画“】+ 实现补间动画和逐帧动画!!!
目录 补间动画 1.创建资源文件夹 2.设置文件夹类型 3.创建.xml文件 4.样式设计 5.动画设置 6.动画的实现 内容拓展 7.在原基础上继续添加.xml文件 8.xml代码编写 (1)rotate_anim (2)scale_anim (3)translate_anim 9.MainActivity.java代码汇总 10.效果展示 逐帧…...
