A Simple Problem with Integers(线段树)
目录
描述
输入
输出
样例输入
样例输出
思路
建树
第一次错误解法(正确解法在下面,可跳过这一步)
正确解法
code
描述
You have N integers, A1, A2, ... , AN. You need to deal with two kinds of operations. One type of operation is to add some given number to each number in a given interval. The other is to ask for the sum of numbers in a given interval.
输入
The first line contains two numbers N and Q. 1 ≤ N,Q ≤ 100000.
The second line contains N numbers, the initial values of A1, A2, ... , AN. -1000000000 ≤ Ai ≤ 1000000000.
Each of the next Q lines represents an operation.
"C a b c" means adding c to each of Aa, Aa+1, ... , Ab. -10000 ≤ c ≤ 10000.
"Q a b" means querying the sum of Aa, Aa+1, ... , Ab.
输出
You need to answer all Q commands in order. One answer in a line.
样例输入
10 5
C 3 6 3
Q 2 4
样例输出
9
15思路
不要看这题全英文,但这题就是属于线段树模版题,基本做法是一样的
建树
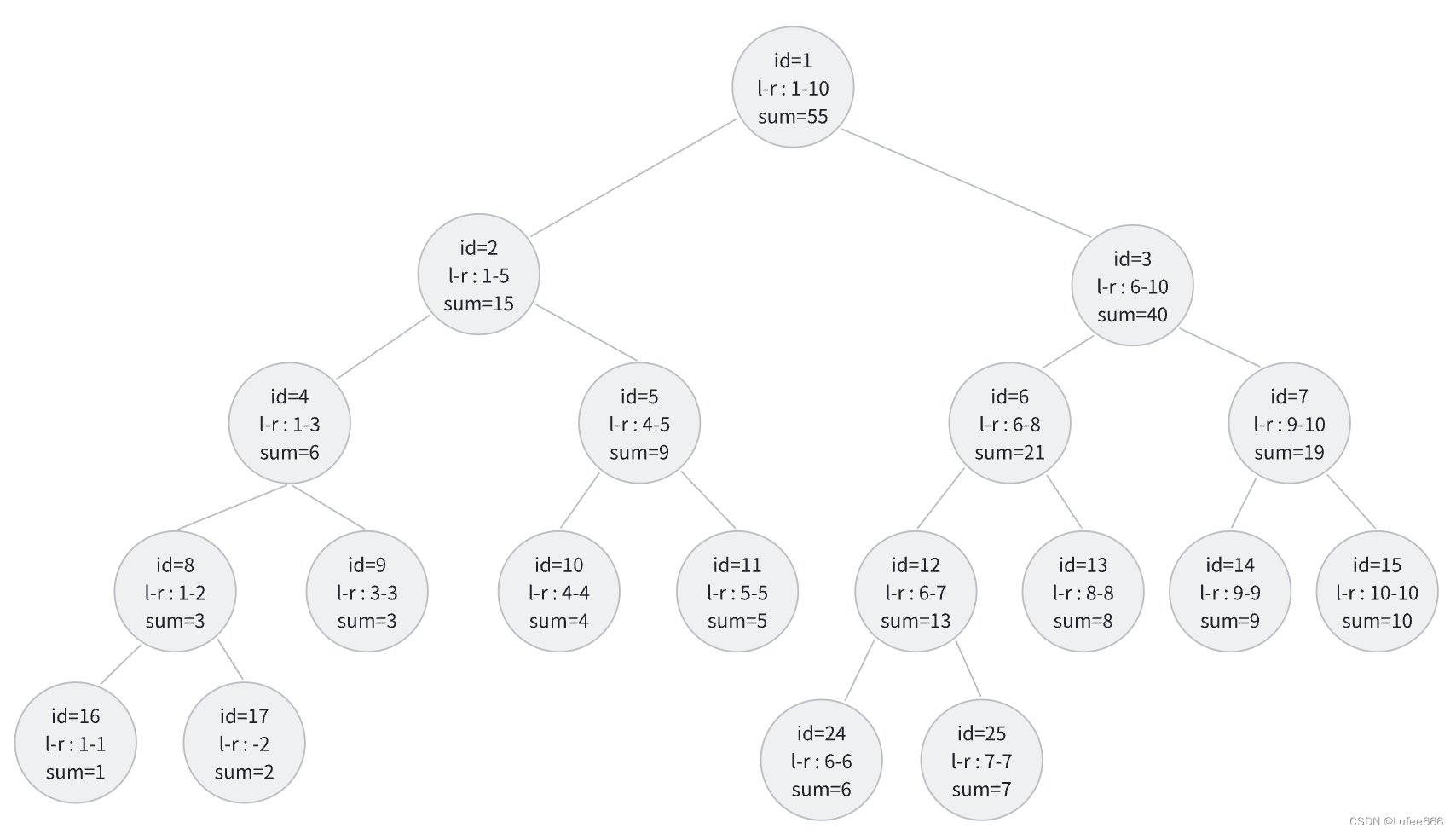
第一次错误解法(正确解法在下面,可跳过这一步)
树没有更新成功,id=10,id=11理论上是要继续更新他们的sum值,但我的错误代码没有更新
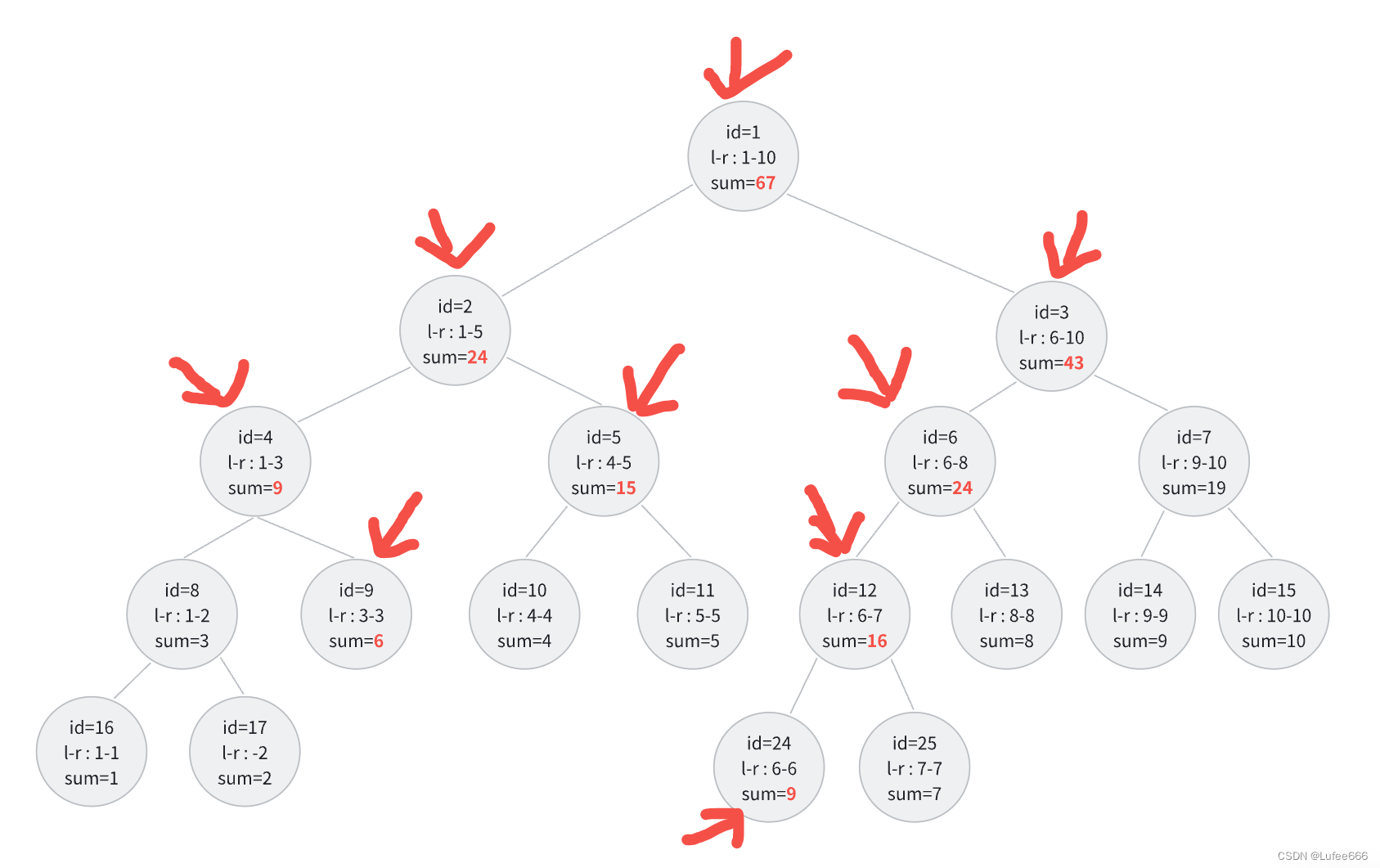
#define _CRT_SECURE_NO_WARNINGS 1
#include<iostream>
using namespace std;
const int N = 100010;
#define ll long long
ll nums[N];
struct Tree {int l, r;ll sum;ll tag;
}tree[N << 2];
void pushup(int u) {tree[u].sum = tree[u << 1].sum + tree[u << 1 | 1].sum;
}
void build(int l, int r, int u) {if (l == r) tree[u] = { l,r,nums[l] };//要与结构体Tree一一对应 else {tree[u] = { l,r };int mid = (l + r) >> 1;build(l, mid, u << 1);build(mid + 1, r, u << 1 | 1);pushup(u);}
}
ll query(int L, int R, int u) {int l = tree[u].l, r = tree[u].r;if (l >= L && r <= R)return tree[u].sum;int mid = (l + r) >> 1;ll sum = 0;if (L <= mid) sum += query(L, R, u << 1);if (R > mid) sum += query(L, R, u << 1 | 1);return sum;
}
void pushdown(int u, int ln, int rn) {if (tree[u].tag) {tree[u << 1].tag += tree[u].tag;tree[u << 1 | 1].tag += tree[u].tag;tree[u << 1].sum += tree[u].tag * ln;tree[u << 1 | 1].sum += tree[u].tag * rn;tree[u].tag = 0;}
}
void updatespan(int L, int R, int value, int u) {int l = tree[u].l, r = tree[u].r;int mid = (l + r) >> 1;if (l >= L && r <= R) {tree[u].tag += value;tree[u].sum += value * (r - l + 1);return;}pushdown(u, mid - l + 1, r - mid);if (L <= mid) updatespan(L, R, value, u << 1);if (R > mid) updatespan(L, R, value, u << 1 | 1);pushup(u);
}
int main()
{int n, q;while (scanf("%d%d", &n, &q) != EOF) {for (int i = 1; i <= n; i++) scanf("%lld", &nums[i]);build(1, n, 1);while (q--) {string cz;int op1, op2;cin >> cz;if (cz == "C") {int val;scanf("%d%d%d", &op1, &op2, &val);updatespan(op1, op2, val, 1);}else {scanf("%d%d", &op1, &op2);printf("%lld\n", query(op1, op2, 1));}}}return 0;
}正确解法
关键在于updatespan函数中,if语句中我没有继续pushdown导致错误
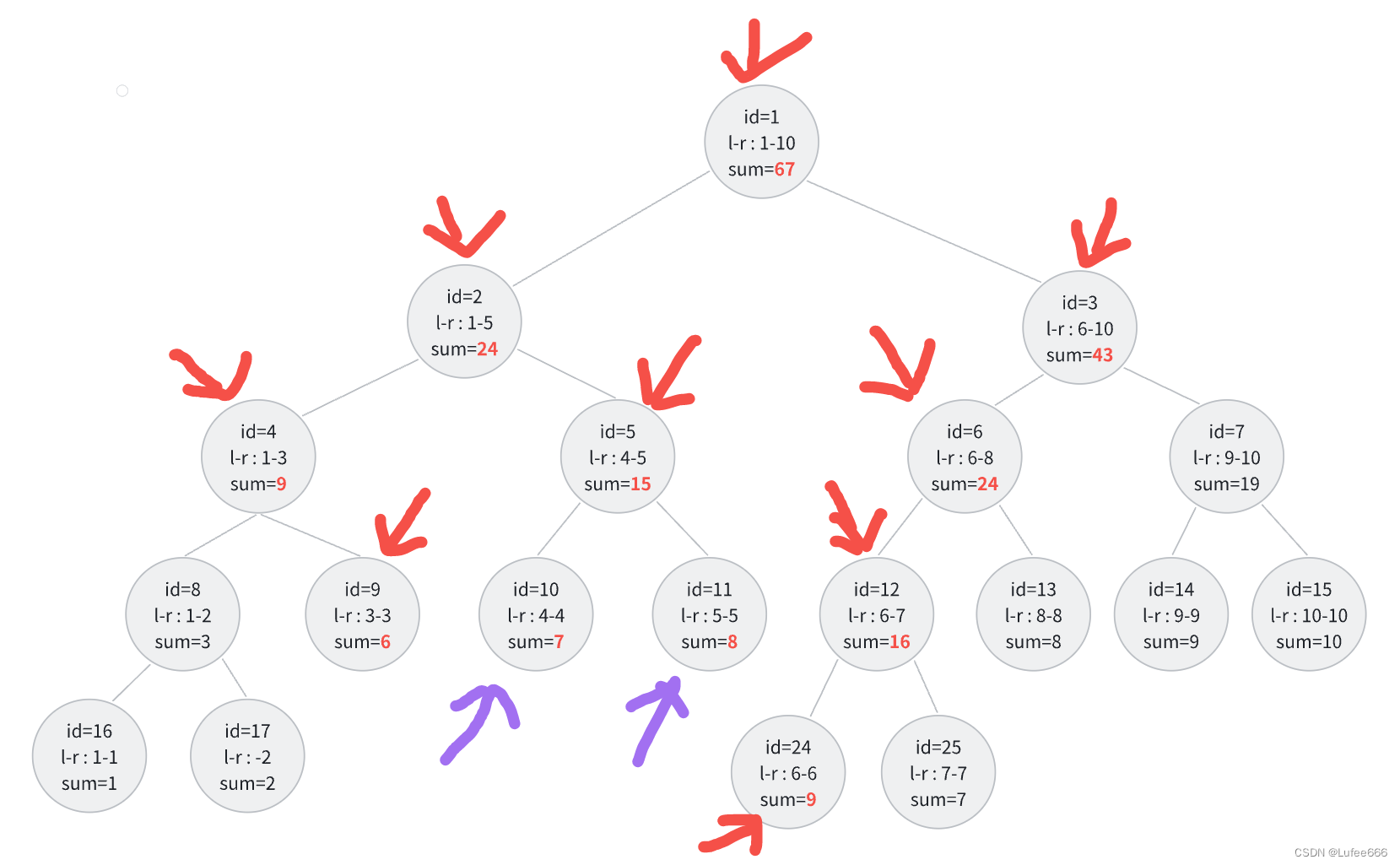
code
#define _CRT_SECURE_NO_WARNINGS 1
#include<iostream>
using namespace std;
const int N = 100010;
#define ll long long
ll nums[N];
struct Tree {int l, r;ll sum;ll tag;
}tree[N << 2];
void pushup(int u) {tree[u].sum = tree[u << 1].sum + tree[u << 1 | 1].sum;
}
void build(int l, int r, int u) {if (l == r) {tree[u] = { l,r,nums[l] };//要与结构体Tree一一对应 else {tree[u] = { l,r };int mid = (l + r) >> 1;build(l, mid, u << 1);build(mid + 1, r, u << 1 | 1);pushup(u);}
}
ll query(int L, int R, int u) {int l = tree[u].l, r = tree[u].r;if (l >= L && r <= R)return tree[u].sum;int mid = (l + r) >> 1;ll sum = 0;if (L <= mid) sum += query(L, R, u << 1);if (R > mid) sum += query(L, R, u << 1 | 1);return sum;
}
void pushdown(int u, int ln, int rn) {if (tree[u].tag) {tree[u << 1].tag += tree[u].tag;tree[u << 1 | 1].tag += tree[u].tag;tree[u << 1].sum += tree[u].tag * ln;tree[u << 1 | 1].sum += tree[u].tag * rn;tree[u].tag = 0;}
}
void updatespan(int L, int R, int value, int u) {int l = tree[u].l, r = tree[u].r;int mid = (l + r) >> 1;if (l >= L && r <= R) {tree[u].tag += value;tree[u].sum += value * (r - l + 1);pushdown(u, mid - l + 1, r - mid);//关键return;}pushdown(u, mid - l + 1, r - mid);if (L <= mid) updatespan(L, R, value, u << 1);if (R > mid) updatespan(L, R, value, u << 1 | 1);pushup(u);
}
int main()
{int n, q;while (scanf("%d%d", &n, &q) != EOF) {for (int i = 1; i <= n; i++) scanf("%lld", &nums[i]);build(1, n, 1);while (q--) {string cz;int op1, op2;cin >> cz;if (cz == "C") {int val;scanf("%d%d%d", &op1, &op2, &val);updatespan(op1, op2, val, 1);}else {scanf("%d%d", &op1, &op2);printf("%lld\n", query(op1, op2, 1));}}}return 0;
}相关文章:

A Simple Problem with Integers(线段树)
目录 描述 输入 输出 样例输入 样例输出 思路 建树 第一次错误解法(正确解法在下面,可跳过这一步) 正确解法 code 描述 You have N integers, A1, A2, ... , AN. You need to deal with two kinds of operations. One type of …...
用例简介)
单元测试(UT)用例简介
单元测试(Unit Testing, UT)用例是一系列预先设计好的、针对软件最小可测试单元的测试场景。每一个单元测试用例都是为了验证一个独立代码单元(如函数、方法、类)的行为是否符合预期。这些用例通常包含以下几个关键组成部分&#…...

Java通过反射机制获取类对象下的属性值
目录 以类USER为例: 使用Java的反射机制获取Column的name为“user_name”的类属性值 以类USER为例: import lombok.Data; import javax.persistence.*; import java.io.Serializable;Data Table(name "user_info") public class User imple…...

IDEA插件开发-File -> New->Project中添加一个myOptions
写一个IDEA插件,在IDEA的File -> New -> Project 中添加一个选项myOptions ,点击myOptions 后弹出一个提示对话框:被点击了 为了在IntelliJ IDEA中创建一个插件,您需要遵循一系列的步骤来开发和集成您的功能。下面是一个简化的指南&am…...
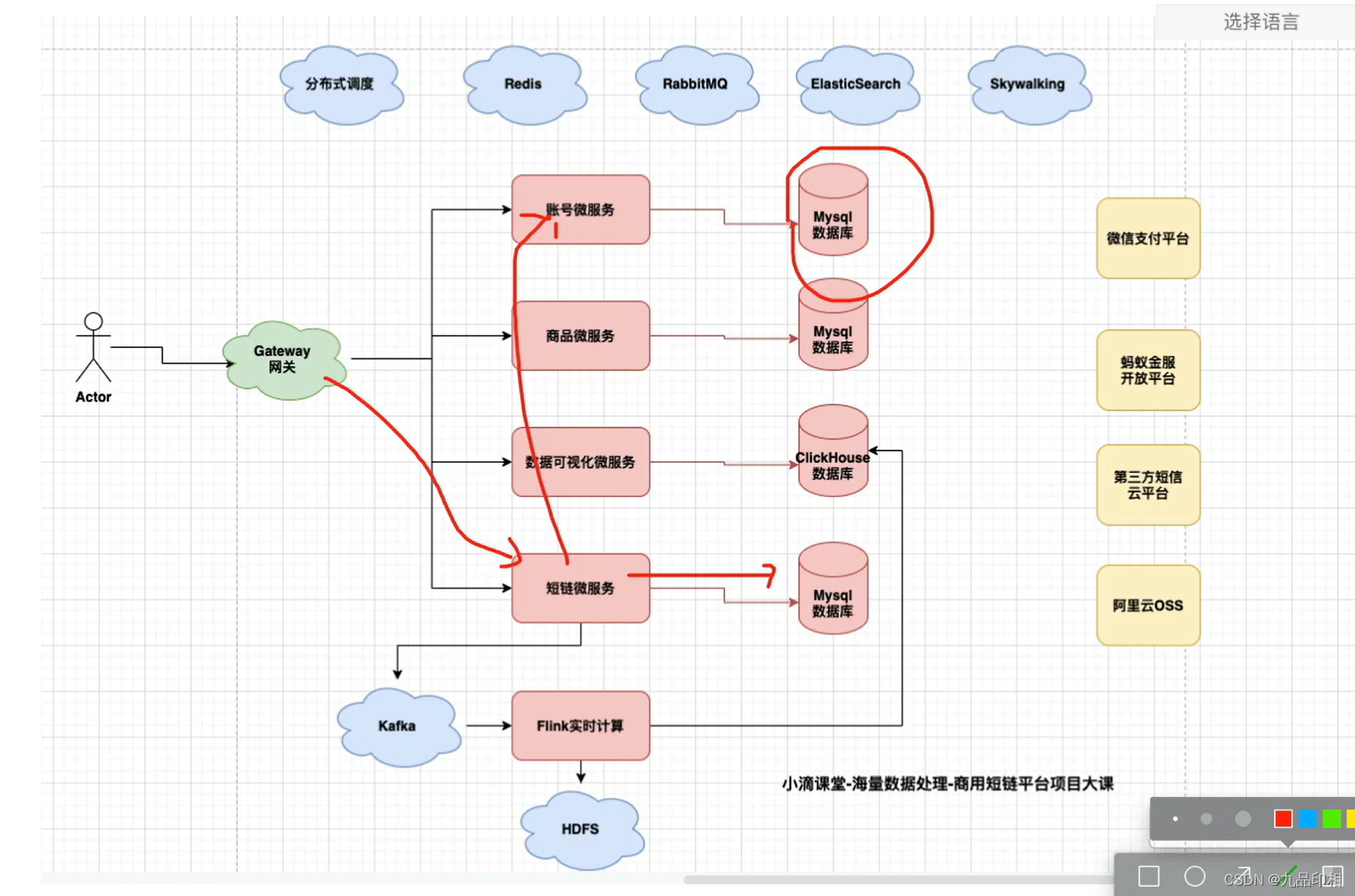
海量数据处理项目-账号微服务和流量包数据库表+索引规范(下)
海量数据处理项目-账号微服务和流量包数据库表索引规范(下) 第2集 账号微服务和流量包数据库表索引规范讲解《下》 简介:账号微服务和流量包数据库表索引规范讲解 账号和流量包的关系:一对多traffic流量包表思考点 海量数据下每…...
Nodejs 16与 gitbook搭建属于你自己的书本网站-第一篇
最近想重新搭建一个网站来存放自己的相关知识点,并向网络公开,有个hexo博客其实也不错的,但是总感觉hexo很多花里胡哨的玩意,导致挂载的博客异常卡,这样反而不利于我自己回顾博客了,于是我就开始钻研这个鬼…...

服务器被CC攻击之后怎么办?
1.取消域名绑定取消域名绑定后Web服务器的CPU能够马上恢复正常状态,通过IP进行访问连接一切正常。但是不足之处也很明显,取消或者更改域名对于别人的访问带来了不变,另外,对于针对IP的CC攻击它是无效的,就算更换域名攻…...

pygame通过重心坐标 用纹理填充三角形
texture_x int(alpha * texture_image.get_width()) texture_y int(beta * texture_image.get_height())为什么没有gama 2024/3/30 15:45:52 在使用重心坐标进行纹理映射时,通常是通过计算 alpha 和 beta 来确定纹理图片上的对应位置,而 gamma 通常是…...

Leetcode 611. 有效三角形的个数
给定一个包含非负整数的数组 nums ,返回其中可以组成三角形三条边的三元组个数。 示例 1: 输入: nums [2,2,3,4] 输出: 3 解释:有效的组合是: 2,3,4 (使用第一个 2) 2,3,4 (使用第二个 2) 2,2,3 示例 2: 输入: nums [4,2,3,4] 输出: 4 提示: 1 < nums.len…...
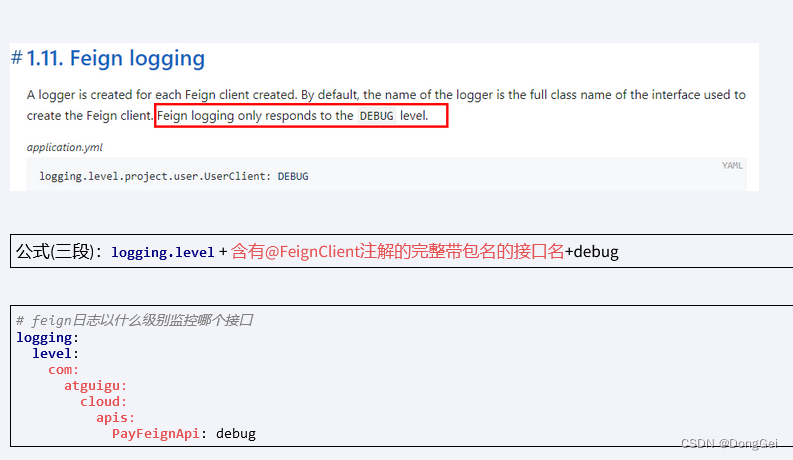
Openfeign
Openfeign 相关扩展 在 2020 以前的 SpringCloud 采用 Ribbon 作为负载均衡,但是 2020 年之后,SpringCloud 吧 Ribbon 移除了,而是使用自己编写的 LoadBalancer 替代. 因此,如果在没有加入 LoadBalancer 依赖的情况下,…...
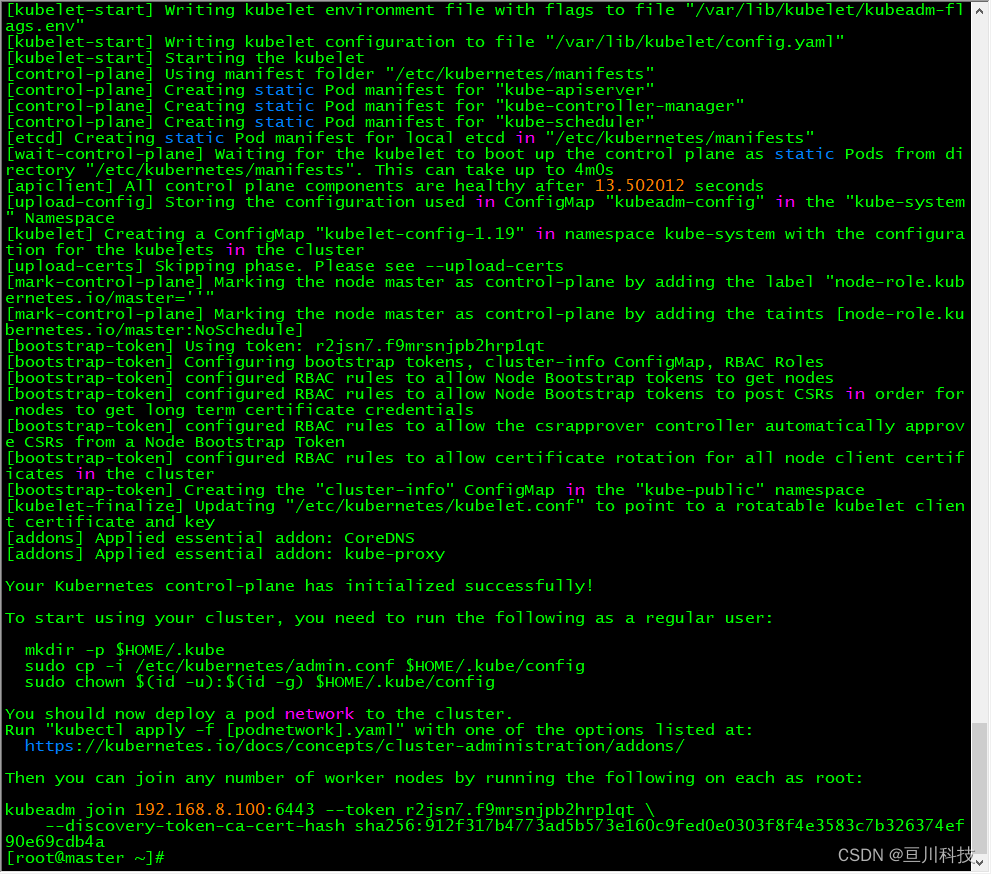
五、基于KubeAdm搭建多节点K8S集群
如需查阅上一步骤,请点击下面链接:四、戴尔R630本地服务器Linux Centos7.9系统安装docker-ce-20.10.10-3.el7版本-CSDN博客文章浏览阅读727次,点赞12次,收藏13次。1、准备工作3、Linux Centos7.9系统的iDRAC远程管理、网络设置、SecureCRT远程登录终端、企业级静态ip地址配…...
PC电脑技巧[笔记本通过网线访问设备CMW500]
笔记本局域网访问设备 现在我有一台CMW500,我要用笔记本去访问它,但是我发现没有路由器就是不能够访问,通过网线连接设备就是ping不通: 这里设置TCP/IPv4的IP地址如下,这时候就可以pin通了:...

【接口自动化测试框架】YAML管理接口框架配置的最佳实践
管理接口框架配置是构建强大的接口测试框架的关键一环。良好的配置管理可以提高测试效率、可维护性和可扩展性。在本文中,我们将重点介绍使用YAML(YAML Ain’t Markup Language)来管理接口框架配置的最佳实践,并通过实例演示其用法…...

【进程OI】基本文件操作的系统调用
文章目录 前言open参数flags参数mode writereadclose 前言 当用户想要向磁盘中的文件读写数据,就必须要得到操作系统的允许。同样,操作系统为了能让用户去对文件进行打开、读写、关闭等操作,向上提供了相应的系统调用的接口。C、JAVA、C等语…...

Ubuntu20.04 server系统部署安装(VMware上)和初始化配置
Ubuntu20.04 server部署安装(VMware上)和初始化配置 一、Ubuntu20.04 server系统部署安装上下键控制上下,可以选择配置的目标,回车表示确定,并进行下一步1.1镜像下载2.1 VMware上创建虚拟机2.2 选择语言,键…...
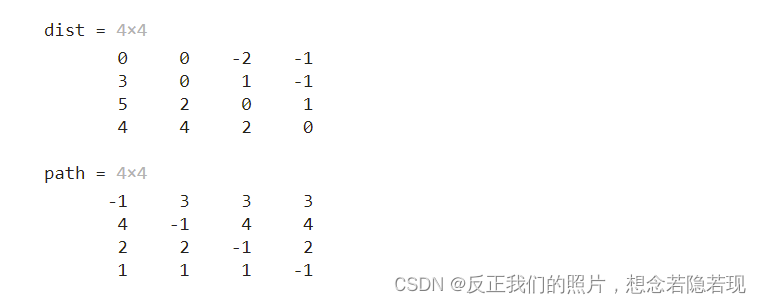
图论最短路径以及floyd算法的MATLAB实现
图论是数学的一个分支,起源于18世纪。1736年,数学家欧拉通过解决“哥尼斯堡七桥问题”,将问题抽象成点和线的关系,并通过理论分析得出结论,这个过程标志着图论的产生,欧拉也因此被称为“图论之父”。图论研…...
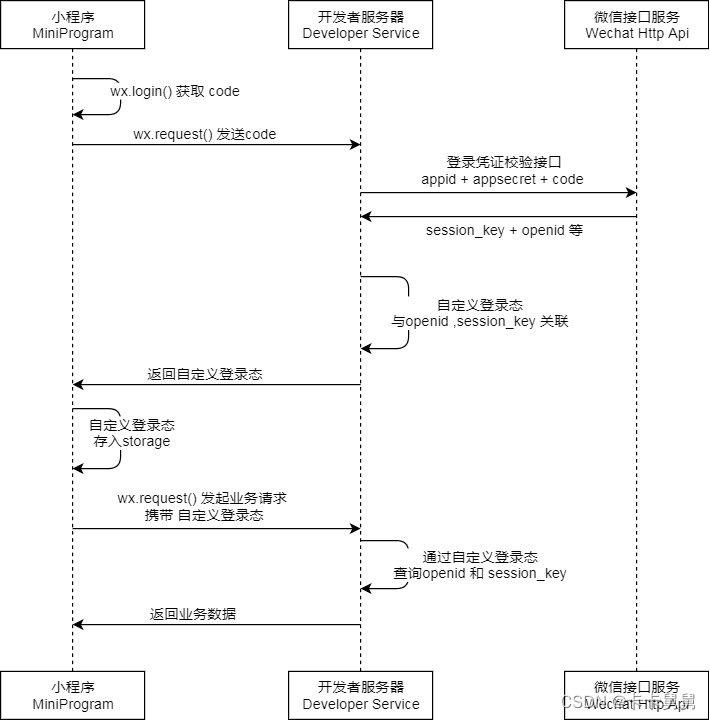
微信小程序 - 登录功能实现
一、认证流程 1. 小程序调用wx.login获取登录认证需要的code,并请求开发者服务器。 2. 开发者服务器根据code,appid, appsecret请求微信接口t获取 openid与session_key ,并生成自己的认证token,并返回给小程序。 3.小程序请求开…...

Python连接MySQL
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 一、整体思路二、连接流程三、表结构及代码实现 一、整体思路 二、连接流程 三、表结构及代码实现 代码块如下: import pymysqlcon pymysql.connect(h…...

水泊梁山108小酒坛之呼保义宋江
宋江【绰号呼保义、及时雨】字公明,是古典名著《水浒传》中的角色。原为山东郓城县押司,他和晁盖互通往来的事被阎婆惜发现,因此怒杀阎婆惜,逃回家隐藏。后前往清风寨投靠花荣,却被清风寨观灯时遭知寨刘高之妻陷害入狱…...

java.lang.ClassNotFoundException: javafx.application.Application
java8(jdk1.8)到java10(jdk10)中内含有JavaFx 在java11(jdk11)以及以后的版本中剥离出来需要开发者独立下载,另行导入download https://gluonhq.com/products/javafx/java --module-path $FX-P…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

面试高频问题
文章目录 🚀 消息队列核心技术揭秘:从入门到秒杀面试官1️⃣ Kafka为何能"吞云吐雾"?性能背后的秘密1.1 顺序写入与零拷贝:性能的双引擎1.2 分区并行:数据的"八车道高速公路"1.3 页缓存与批量处理…...

Neko虚拟浏览器远程协作方案:Docker+内网穿透技术部署实践
前言:本文将向开发者介绍一款创新性协作工具——Neko虚拟浏览器。在数字化协作场景中,跨地域的团队常需面对实时共享屏幕、协同编辑文档等需求。通过本指南,你将掌握在Ubuntu系统中使用容器化技术部署该工具的具体方案,并结合内网…...

数据结构第5章:树和二叉树完全指南(自整理详细图文笔记)
名人说:莫道桑榆晚,为霞尚满天。——刘禹锡(刘梦得,诗豪) 原创笔记:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 上一篇:《数据结构第4章 数组和广义表》…...

文件上传漏洞防御全攻略
要全面防范文件上传漏洞,需构建多层防御体系,结合技术验证、存储隔离与权限控制: 🔒 一、基础防护层 前端校验(仅辅助) 通过JavaScript限制文件后缀名(白名单)和大小,提…...
