深度学习入门简单实现一个神经网络
实现一个三层神经网络
- 引言
- 测试数据
- 代码
引言
今天我们实现一个简单的神经网络
俩个输入神经元 隐藏层两个神经元 一个输出神经元
激活函数我们使用sigmoid
优化方法使用梯度下降

我们前期准备是需要把这些神经元的关系理清楚
x1:第一个输入
x2:第二个输入
w11_1:第一层的第一个神经元在第一个输入上的权重
w12_1:第一层的第二个神经元在第一个输入上的权重
b1_1:第一层第一个神经元的偏置项(截距)
z1_1:第一层第一个神经元的线性函数
a1_1:第一层第一个神经元的激活函数
w21_1:第一层的第一个神经元在第一个输入上的权重
w22_1:第一层的第一个神经元在第一个输入上的权重
b2_1:第一层第二个神经元的偏置项(截距)
z1_1:第一层第二个神经元的线性函数
a1_1:第一层第二个神经元的激活函数
w11_2:第二层的第一个神经元在第一个输入上的权重
w21_2:第二层的第二个神经元在第一个输入上的权重
b1_2:第二层第一个神经元的偏置项(截距)
z1_1:第二层第一个神经元的线性函数
a1_1:第二层第一个神经元的激活函数
e:损失函数
测试数据
dataset 可以使用西瓜书89页的西瓜数据集3.0α
代码
import numpy as np
import sympy
import dataset
from matplotlib import pyplot as pltdef sigmod(b):return 1 / (1 + np.exp(-b))xs, ys = dataset.get_beans(100) # 获取数据
plt.title("Size-Toxicity Funciton", fontsize=12) # 设置图片的标题
plt.xlabel("Bean Size") # 设置行标签
plt.ylabel("Toxicity") # 设置列标签plt.scatter(xs, ys) # 画散点图"""
命名规则
下划线后面的数字表示被输入的神经元所在的层数
字母后面的数字表示第一个数字表示第几个输入
第二个数字表示被输入的神经元在他所在层数的位置
"""
# 第一层
# 第一个神经元
w11_1 = np.random.rand()
b1_1 = np.random.rand()
# 第二个神经元
w12_1 = np.random.rand()
b2_1 = np.random.rand()
# 第二层
w11_2 = np.random.rand()
w21_2 = np.random.rand()
b1_2 = np.random.rand()# 前向传播 代价函数 y0 = 1/(1+e^(-(wx+b)))
def forward_propgation(xs):z1_1 = w11_1 * xs + b1_1a1_1 = sigmod(z1_1) # 第一层第一个神经元的代价函数值z2_1 = w12_1 * xs + b2_1a2_1 = sigmod(z2_1) # 第一层第二个神经元的代价函数值z1_2 = w11_2 * a1_1 + w21_2 * a2_1 + b1_2a1_2 = sigmod(z1_2) # 第二层第一个神经元的代价函数值return a1_2, z1_2, a2_1, z2_1, a1_1, z1_1a1_2, z1_2, a2_1, z2_1, a1_1, z1_1 = forward_propgation(xs)
# plt.plot(xs, a1_2)
# plt.show()# 随机梯度下降
for j in range(5000):for i in range(100):x = xs[i]y = ys[i]# 先来一次前向传播a1_2, z1_2, a2_1, z2_1, a1_1, z1_1 = forward_propgation(x)# 开始反向传播# 误差代价函数e"""z1_1 = w11_1 * xs + b1_1a1_1 = sigmod(z1_1) # 第一层第一个神经元的代价函数值z2_1 = w12_1 * xs + b2_1a2_1 = sigmod(z2_1) # 第一层第二个神经元的代价函数值z1_2 = w11_2 * a1_1 + w21_2 * a2_1a1_2 = sigmod(z1_2) # 第二层第一个神经元的代价函数值"""e = (y - a1_2) ** 2 # 误差e = (y - 最后一个神经元得出的值)^2deda1_2 = -2*(y - a1_2) # 对a1_2 第二层的第一个神经元的函数求导da1_2dz1_2 = a1_2 * (1 - a1_2) # da1_2对dz1_2求导数dz1_2dw11_2 = a1_1 # dz1_2对w11_2求导数dz1_2dw21_2 = a2_1 # dz1_2对dw21_2求导dedw11_2 = deda1_2 * da1_2dz1_2 * dz1_2dw11_2 # de对dw11_2求偏导dedw21_2 = deda1_2 * da1_2dz1_2 * dz1_2dw21_2 # de对dw21_2求偏导dz1_2db1_2 = 1 # z1_2对db1_2求偏导dedb1_2 = deda1_2 * da1_2dz1_2 * dz1_2db1_2 # de对db1_2求偏导dz1_2da1_1 = w11_2 # dz1_2对da1_1求偏导da1_1dz1_1 = a1_1 * (1 - a1_1) # da1_1对dz1_1 求偏导dz1_1dw11_1 = x # dz1_1对dw11_1求偏导dedw11_1 = deda1_2 * da1_2dz1_2 * dz1_2da1_1 * da1_1dz1_1 * dz1_1dw11_1 # e对w11_1求导dz1_1db1_1 = 1 # z1_1对b1_1求导dedb1_1 = deda1_2 * da1_2dz1_2 * dz1_2da1_1 * da1_1dz1_1 * dz1_1db1_1 # e对b1_1求导dz1_2da2_1 = w21_2 # z1_2 对a2_1 求导da2_1dz2_1 = a2_1 * (1 - a2_1) # a2_1 对z2_1求导dz2_1dw12_1 = x # z2_1对w12_1dedw12_1 = deda1_2 * da1_2dz1_2 * dz1_2da1_1 * da2_1dz2_1 * dz2_1dw12_1 # e对w12_1求导dz2_1db2_1 = 1 # z2_1 对 b2_1求导dedb2_1 = deda1_2 * da1_2dz1_2 * dz1_2da1_1 * da2_1dz2_1 * dz2_1db2_1 # e 对 b2_1求导alpha = 0.03w11_2 = w11_2 - alpha * dedw11_2 # 调整w11_2w21_2 = w21_2 - alpha * dedw21_2 # 调整21_2b1_2 = b1_2 - alpha * dedb1_2 # 调整b1_2w12_1 = w12_1 - alpha * dedw12_1 # 调整w12_1b2_1 = b2_1 - alpha * dedb2_1 # 调整 b2_1w11_1 = w11_1 - alpha * dedw11_1 # 调整 w11_1b1_1 = b1_1 - alpha * dedb1_1 # 调整b1_1if j % 100 == 0:plt.clf() # 清空窗口plt.scatter(xs, ys)a1_2, z1_2, a2_1, z2_1, a1_1, z1_1 = forward_propgation(xs)plt.plot(xs, a1_2)plt.pause(0.01) # 暂停0.01秒相关文章:

深度学习入门简单实现一个神经网络
实现一个三层神经网络 引言测试数据 代码 引言 今天我们实现一个简单的神经网络 俩个输入神经元 隐藏层两个神经元 一个输出神经元 激活函数我们使用sigmoid 优化方法使用梯度下降 我们前期准备是需要把这些神经元的关系理清楚 x1:第一个输入 x2:第二个…...

win11 环境配置 之 Jmeter(JDK17版本)
一、安装 JDK 1. 安装 jdk 截至当前最新时间: 2024.3.27 jdk最新的版本 是 官网下载地址: https://www.oracle.com/java/technologies/downloads/ 建议下载 jdk17 另存为到该电脑的 D 盘下,新建jdk文件夹 开始安装到 jdk 文件夹下 2. 配…...
Windows下载使用nc(netcat)命令
‘nc’ 不是内部或外部命令,也不是可运行的程序? 点击链接地址,下载压缩包。 完成后解压 使用方式(三种): 1、直接双击exe使用 2、把这个exe放到cmd启动的默认路径下 放到默认路径下,使用nc&a…...
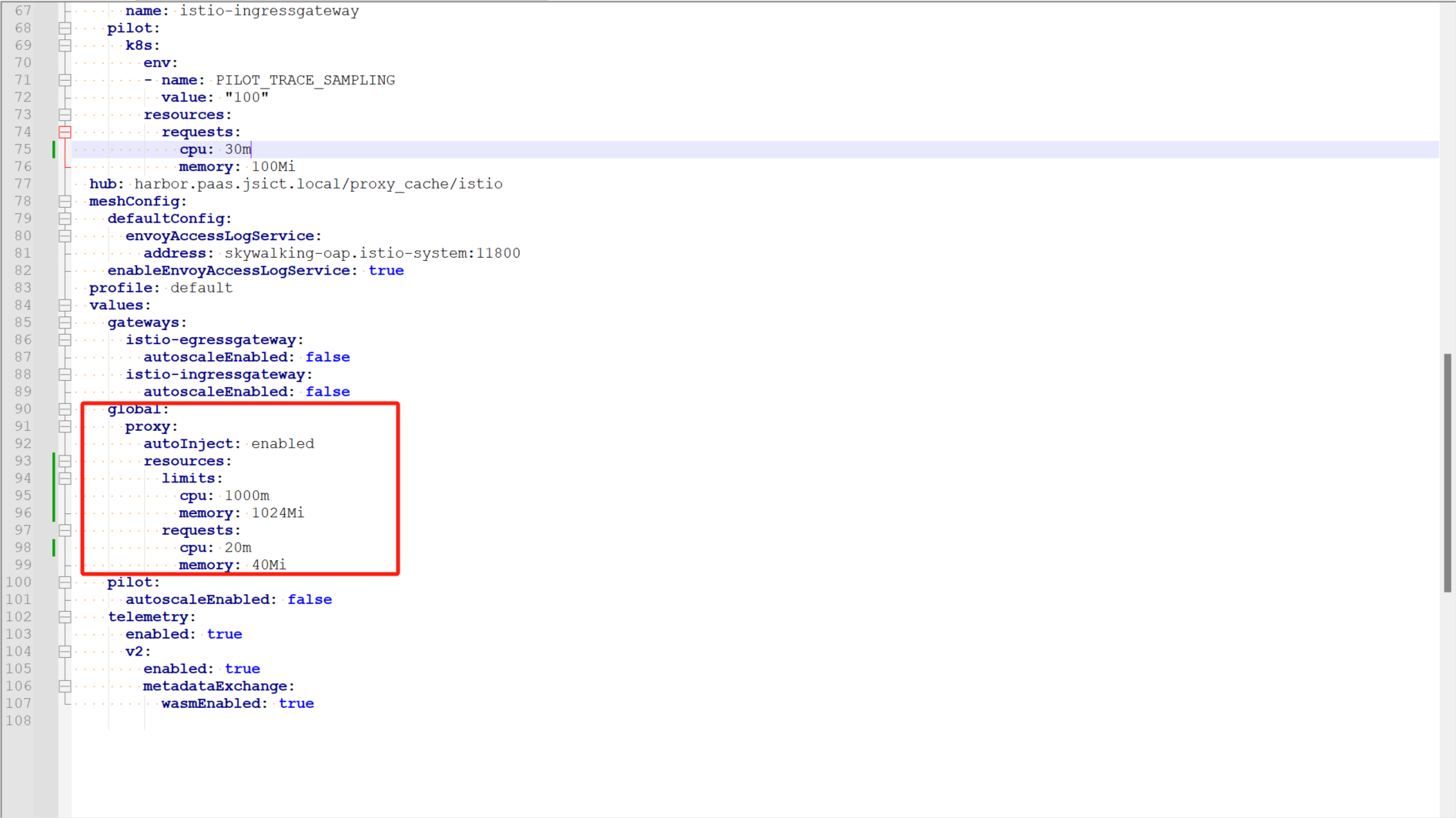
istio 设置 istio-proxy sidecar 的 resource 的 limit 和 request
方式一 修改 configmap 查看当前 sidecar 的 cpu 和 memory 的配额 在 istio-sidecar-injector 中查找,修改后重启 pod 可以生效(下面那个 proxy_init 配置不管,不知道是干嘛的) 方式二 如果是通过 iop 安装的 istio…...

flutter弹框
alertDialog:弹框 simpleDialog:选择弹框 showModalBottomSheet:底部弹出弹框 showtoast:三方插件弹框 Navigator.of(context).pop(点击取消) 关闭弹框,传递参数 import package:flutter/material.dart; // import package:flutter/cupertino.dart; import package:flut…...

2013年认证杯SPSSPRO杯数学建模B题(第一阶段)流行音乐发展简史全过程文档及程序
2013年认证杯SPSSPRO杯数学建模 B题 流行音乐发展简史 原题再现: 随着互联网的发展,流行音乐的主要传播媒介从传统的电台和唱片逐渐过渡到网络下载和网络电台等。网络电台需要根据收听者的已知喜好,自动推荐并播放其它音乐。由于每个人喜好…...

代码随想录算法训练营第39天 | 62.不同路径, 63不同路径II
Leetcode - 62:不同路径 题目: 一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” &#…...

Redis 的慢日志
Redis 的慢日志 Redis 的慢日志(Slow Log)是用于记录执行时间超过预设阈值的命令请求的系统。慢日志可以帮助运维人员和开发人员识别潜在的性能瓶颈,定位那些可能导致 Redis 性能下降或响应延迟的慢查询。以下是 Redis 慢日志的相关细节&…...

第十四届蓝桥杯第十题:蜗牛分享
问题描述 输入格式 输出格式 输出共一行,一个浮点数表示答案(四舍五入保留两位小数)。 样例输入 3 1 10 11 1 1 2 1样例输出 4.20样例说明 蜗牛路线:(0,0)→(1,0)→(1,1)→(10,1)→(10,0)→(11,0)(0,0)→(1,0)→(1,1)→(10,1…...

不懂技术的老板,如何避免过度依赖核心技术人员
在这个日新月异、技术驱动的时代,即使作为非技术背景的老板,也深知核心技术人员的价值。然而,过度依赖某几位核心技术人员,不仅可能带来经营风险,还可能限制企业的创新与发展。那么,不懂技术的老板…...

Vue系列-el挂载
<!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>el:挂载点</title> </head> <body&g…...

python--os和os.path模块
>>> import os >>> #curdir #获取当前脚本的绝对路径 >>> os.curdir . >>> import os.path >>> #获取绝对路径 >>> os.path.abspath(os.curdir) C:\\Users\\GUOGUO>>> #chdir #修改当前目录 >&g…...

前端通用命名规范和Vue项目命名规范
通用命名规范 变量和常量命名:变量和常量的命名应具有描述性,清晰明了,使用驼峰命名法或下划线命名法,例如:firstName、MAX_VALUE。 函数和方法命名:函数和方法的命名应该能够准确描述其功能&…...

NTP服务搭建
一、ntpd和ntpdate区别 1.ntpd是自动执行的远程更新本地系统时钟的服务,是平滑同步; 2.ntpdate是手工执行的服务,也就是一般用它执行一次本地时间更新,如果做成半自动,可以写入到crontab自动任务,从而变成…...

Linux离线安装mysql,node,forever
PS:本文是基于centos7实现的,要求系统能够查看ifconfig和unzip解压命令, 实现无网络可安装运行 首先现在百度网盘的离线文件包****安装Xftp 和 Xshell 把机房压缩包传到 home目录下****解压unzip 包名.zip 获取IP先获取到 linux 主机的ip ifconfig Xftp 连接输入IP,然后按照…...
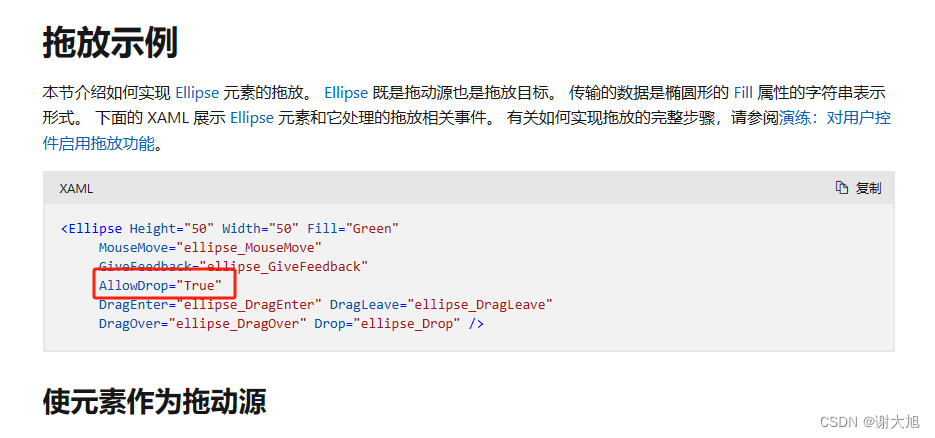
WPF中获取TreeView以及ListView获取其本身滚动条进行滚动
实现自行调节scoll滚动的位置(可相应获取任何控件中的内部滚动条) TreeView:TreeViewAutomationPeer lvap new TreeViewAutomationPeer(treeView); var svap lvap.GetPattern(PatternInterface.Scroll) as ScrollViewerAutomationPeer; var scroll svap.Owner as ScrollVie…...

C语言: 指针讲解
为什么需要指针? (1)指针的使用使得不同区域的代码可以轻易的共享内存数据。当然你也可以通过数据的复制达到相同的效果,但是这样往往效率不太好,因为诸如结构体等大型数据,占用的字节数多,复制很消耗性能…...

C#使用Stopwatch类来实现计时功能
前言 在 C# 中,Stopwatch 类是用于测量经过的时间的工具类,提供了高精度的计时功能。Stopwatch 类位于 System.Diagnostics 命名空间中。通常情况下,使用 Stopwatch 的流程是创建一个 Stopwatch 对象,然后调用 Start 方法开始计时…...

ubuntu18.04安装qt
ubuntu18.04安装qt 1、下载文件 比如我下载的是5.13.0版本 下载链接 2、安装 wget https://download.qt.io/archive/qt/5.13/5.13.0/qt-opensource-linux-x64-5.13.0.runsudo chmod x qt-opensource-linux-x64-5.13.0.runsudo ./qt-opensource-linux-x64-5.13.0.run参考文…...
ElasticSearch、java的四大内置函数式接口、Stream流、parallelStream背后的技术、Optional类
第四周笔记 一、ElasticSearch 1.安装 apt-get install lrzsz adduser -m es 创建用户组: useradd *-m* xiaoming(用户名) *PS:追加参数-m* passwd xiaoming(用户名) passwd xiaoming 输入新的 UNIX 密码: 重新输入新的 UNIX 密码&…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...

基于单片机的宠物屋智能系统设计与实现(论文+源码)
本设计基于单片机的宠物屋智能系统核心是实现对宠物生活环境及状态的智能管理。系统以单片机为中枢,连接红外测温传感器,可实时精准捕捉宠物体温变化,以便及时发现健康异常;水位检测传感器时刻监测饮用水余量,防止宠物…...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...

Linux基础开发工具——vim工具
文章目录 vim工具什么是vimvim的多模式和使用vim的基础模式vim的三种基础模式三种模式的初步了解 常用模式的详细讲解插入模式命令模式模式转化光标的移动文本的编辑 底行模式替换模式视图模式总结 使用vim的小技巧vim的配置(了解) vim工具 本文章仍然是继续讲解Linux系统下的…...
