数据结构 - 算法效率|时间复杂度|空间复杂度
目录
1.算法效率
2.时间复杂度
2.1定义
2.2大O渐近表示法
2.3常见时间复杂度计算举例
3.空间复杂度
3.1定义
3.2常见空间复杂度计算举例
1.算法效率
算法的效率常用算法复杂度来衡量,算法复杂度描述了算法在输入数据规模变化时,其运行时间和空间占用情况的变化趋势。
算法在编写成可执行程序后,运行时需要耗费时间资源和空间(内存)资源,所以我们常从时间和空间两个维度来评判算法的好坏,即时间复杂度和空间复杂度。
在计算机诞生之初,储存容量很小,所以对于空间很是在意,但随着计算机行业的迅速发展,计算机的存储容量已经达到了很高的程度,所以我们如今已经不需要再特别关注一个算法的空间复杂度。
2.时间复杂度
2.1定义
时间复杂度是衡量算法执行所需时间的指标,表示算法执行时间随输入规模增加而增长的速度。
在计算机科学中,算法的时间复杂度是一个函数,它定量描述了该算法的运行时间。一个算法执行所耗费的时间,从理论上说,是不能算出来的,只有我们把的程序放在机器上跑起来,才能知道。但是我们需要每个算法都上机测试吗?是可以都上机测试,但是这很麻烦,所以才有了时间复杂度这个分析方式。
一个算法所花费的时间与其中语句的执行次数成正比例,算法中的基本操作的执行次数,为算法的时间复杂度。
2.2大O渐近表示法
大O渐近表示法是一种用于描述算法时间复杂度的符号表示方法。它表示算法的最坏情况下执行时间的上界。在大O表示法中,O后面跟着一个函数,表示该函数的增长率与输入规模的关系。
大O渐近表示法的推导:
- 用常数1取代运行时间中的所有加法常数。
- 在修改后的运行次数函数中,只保留最高阶项。
- 如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。
大O的渐进表示法去掉了那些对结果影响不大的项,简洁明了的表示出了执行次数。
下面以一段代码介绍大O渐近表示法的推导:
#include<stdio.h>
void Func1(int N)
{int count = 0;for (int i = 0; i < N; ++i){for (int j = 0; j < 2 * N; ++j){++count;}}for (int k = 0; k < 2 * N; ++k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}int main()
{Func1(5);return 0;
}
可以看出
F(N) = N * (2 * N) + 2 * N + 10
首先我们用常数1取代运行时间中的所有加法常数:
F(N) = N * (2 * N) + 2 * N + 1
然后保留最高阶项:
F(N) = 2 * N^2
如果最高阶项存在且不是1,则去除与这个项目相乘的常数:
F(N) = N^2
即:
O(N^2)
2.3常见时间复杂度计算举例
void Func1(int N, int M)
{int count = 0;for (int k = 0; k < M; ++ k){++count;}for (int k = 0; k < N ; ++ k){++count;}printf("%d\n", count);
}
时间复杂度:O(M + N)
void Func2(int N)
{int count = 0;for (int k = 0; k < 100; ++ k){++count;}printf("%d\n", count);
}
时间复杂度:O(1)
void bubbleSort(int arr[], int n)
{int i, j, temp;for (i = 0; i < n-1; i++) {for (j = 0; j < n-i-1; j++) {if (arr[j] > arr[j+1]) {temp = arr[j];arr[j] = arr[j+1];arr[j+1] = temp;}}}
}对于长度为n的数组,冒泡排序的最坏情况时间复杂度为O(n^2)。这是因为在最坏情况下,需要进行n-1轮比较和交换,每轮最多需要进行n-1次比较和交换操作。
在最好情况下,即输入数组已经是有序的,冒泡排序只需要进行一次遍历,即O(n)的时间复杂度
所以它的大O渐近表示法:
O(N^2)
int BinarySearch(int* a, int n, int x)
{assert(a);int begin = 0;int end = n - 1;while (begin < end){int mid = begin + ((end - begin) >> 1);if (a[mid] < x)begin = mid + 1;else if (a[mid] > x)end = mid;elsereturn mid;}return -1;
}
二分查找的时间复杂度为 O() ,因为每一次迭代都会将查找范围减半。因此,总的查找时间取决于进行了多少次这样的迭代。由于每次迭代都将查找范围减半,所以查找时间以对数的方式增长,即时间复杂度为 O(
)
long long Fac(size_t N)
{if (0 == N)return 1;return Fac(N - 1) * N;
}每次调用函数 Fac(N),都会产生一个新的函数调用 Fac(N - 1),直到 N 减小到 0 为止。因此,这个递归树的深度为 N。在每一层递归中,都会进行一次乘法运算。
因此,这个递归函数的时间复杂度为 O(N)
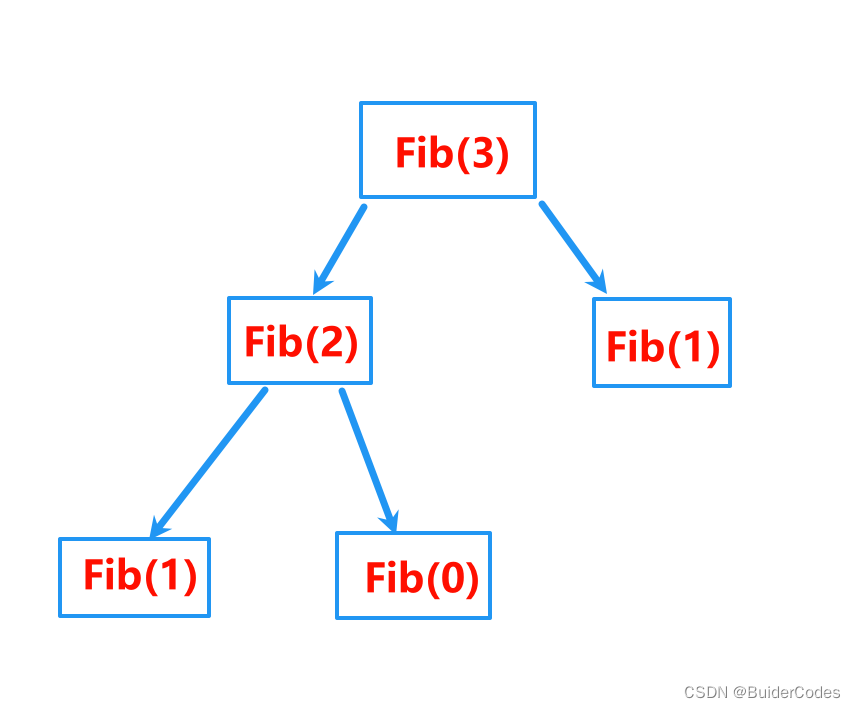
long long Fib(size_t N)
{if (N < 3)return 1;return Fib(N - 1) + Fib(N - 2);
}
要计算这个递归函数的时间复杂度,可以使用递归树的方法来分析(如下图)。在递归树中,每个节点代表一次函数调用,树的高度表示递归的深度,而每层的节点数表示每次递归调用的次数。
对于斐波那契数列的递归函数,由于每次调用会分解为两个子问题(计算第N-1项和第N-2项),因此递归树的分支数是2且每个节点的时间复杂度都是O(1),因为每次递归调用都只涉及一次加法运算。递归的深度为N。
因此,这个递归函数的时间复杂度是 O(2^N),因为递归树的分支数是2,且深度为N。
3.空间复杂度
3.1定义
空间复杂度也是一个数学表达式,是对一个算法在运行过程中临时开辟的额外占用存储空间大小的量度 。
‘额外’的解释:函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了,此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。
空间复杂度不是用程序占用了多少字节的空间来衡量,因为这样意义不大,空间复杂度算的是变量的个数。 空间复杂度计算规则基本跟时间复杂度类似,也使用大O渐进表示法。
3.2常见空间复杂度计算举例
long long Fac(size_t N)
{if (N == 0)return 1;return Fac(N - 1) * N;
}
递归函数的空间复杂度取决于递归调用的深度。每次递归调用都会在内存中创建一个新的函数调用帧(包含函数的参数、局部变量等信息)。由于递归调用的次数与输入参数 N 的大小成正比,因此空间复杂度为 O(N)。
long long Fib(size_t N)
{if (N < 3)return 1;return Fib(N - 1) + Fib(N - 2);
}
这个斐波那契函数的时间复杂度我们已经计算过为O(2^N),那么它的空间复杂度也为 O(2^N) 吗?
先说结论,斐波那契函数的空间复杂度为O(N)。
这与函数的调用有关,要知道在函数调用时不是Fib(N - 1) 和 Fib(N - 2)一起调用的,而是调用Fib(N - 1) --> Fib(N - 2) --> ....... Fib(2)这样一层一层的调用的,每次调完上一层对的函数栈帧就已经销毁了。
所以:时间是一去不复返的,而空间是可以重复利用的。
函数栈帧详细信息见:
https://blog.csdn.net/BuiderCodes/article/details/136876577![]() https://blog.csdn.net/BuiderCodes/article/details/136876577
https://blog.csdn.net/BuiderCodes/article/details/136876577
相关文章:
数据结构 - 算法效率|时间复杂度|空间复杂度
目录 1.算法效率 2.时间复杂度 2.1定义 2.2大O渐近表示法 2.3常见时间复杂度计算举例 3.空间复杂度 3.1定义 3.2常见空间复杂度计算举例 1.算法效率 算法的效率常用算法复杂度来衡量,算法复杂度描述了算法在输入数据规模变化时,其运行时间和空间…...
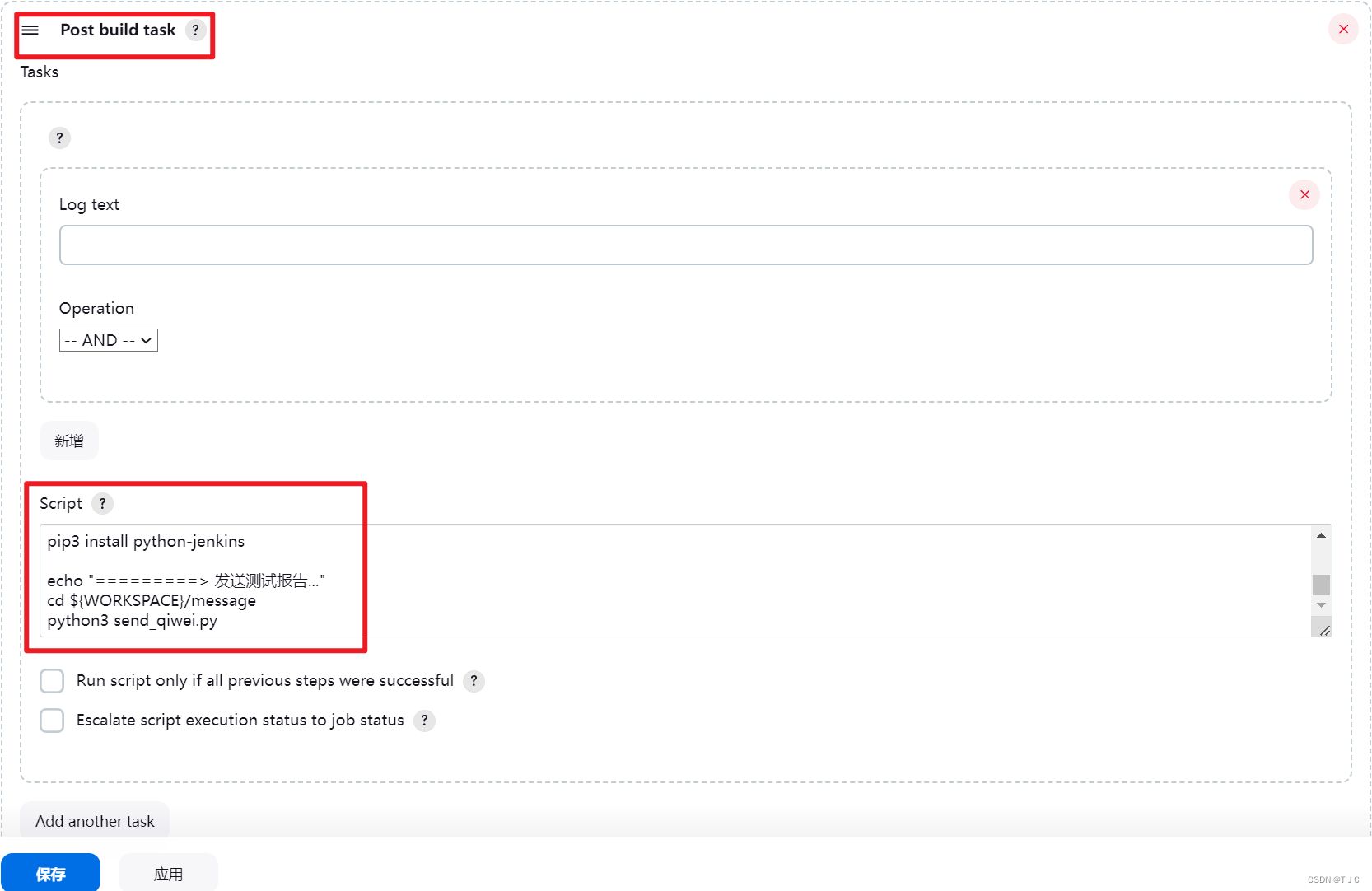
接口自动化之 + Jenkins + Allure报告生成 + 企微消息通知推送
接口自动化之 Jenkins Allure报告生成 企微消息通知推送 在jenkins上部署好项目,构建成功后,希望可以把生成的报告,以及结果统计发送至企微。 效果图: 实现如下。 1、生成allure报告 a. 首先在Jenkins插件管理中&#x…...

『Apisix安全篇』探索Apache APISIX身份认证插件:从基础到实战
🚀『Apisix系列文章』探索新一代微服务体系下的API管理新范式与最佳实践 【点击此跳转】 📣读完这篇文章里你能收获到 🛠️ 了解APISIX身份认证的重要性和基本概念,以及如何在微服务架构中实施API安全。🔑 学习如何使…...
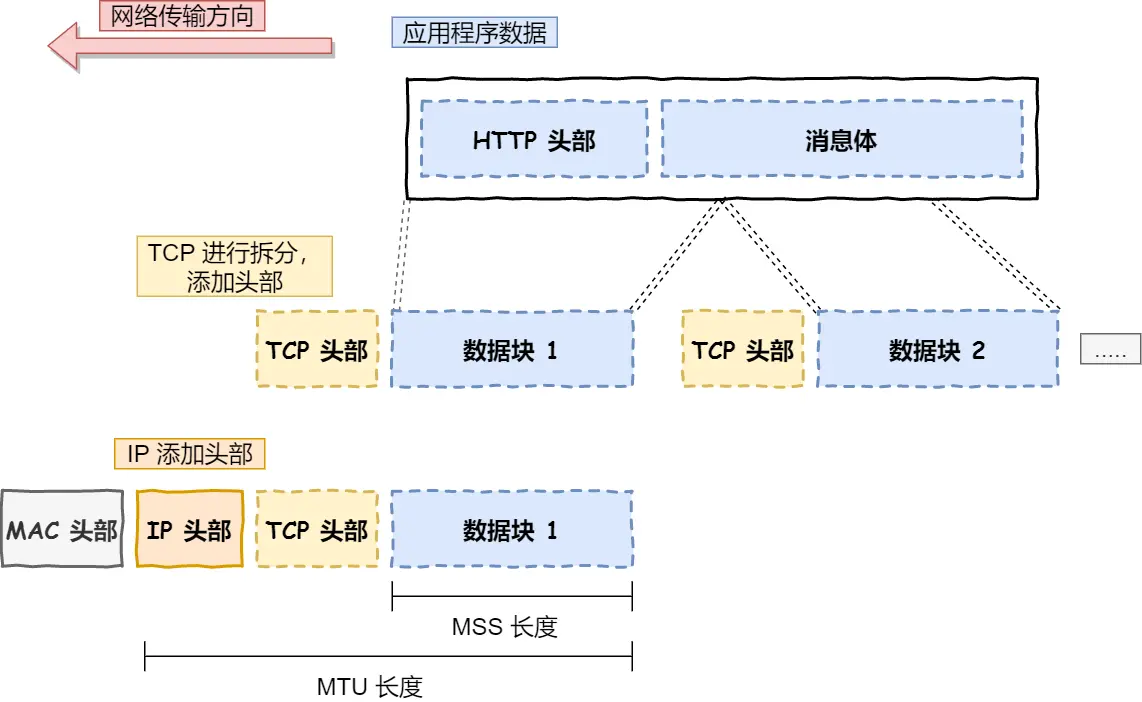
【01-20】计算机网络基础知识(非常详细)从零基础入门到精通,看完这一篇就够了
【01-20】计算机网络基础知识(非常详细)从零基础入门到精通,看完这一篇就够了 以下是本文参考的资料 欢迎大家查收原版 本版本仅作个人笔记使用1、OSI 的七层模型分别是?各自的功能是什么?2、说一下一次完整的HTTP请求…...
)
『大模型笔记』常见的分布式并行策略(分布式训练)
常见的分布式并行策略(分布式训练) 文章目录 一. 为什么分布式训练越来越流行二. 常见的并行策略2.1 数据并行2.2 模型并行2.3 流水并行2.4 混合并行二. 参考文献一. 为什么分布式训练越来越流行 近年来,深度学习被广泛应用到各个领域,包括计算机视觉、语言理解、语音识别、广…...
java 企业工程管理系统软件源码+Spring Cloud + Spring Boot +二次开发+ 可定制化
工程项目管理软件是现代项目管理中不可或缺的工具,它能够帮助项目团队更高效地组织和协调工作。本文将介绍一款功能强大的工程项目管理软件,该软件采用先进的Vue、Uniapp、Layui等技术框架,涵盖了项目策划决策、规划设计、施工建设到竣工交付…...
3D数据格式导出工具HOOPS Publish如何生成高质量3D PDF?
在当今数字化时代,从建筑设计到制造业,从医学领域到电子游戏开发,3D技术已经成为了不可或缺的一部分。在这个进程中,将3D模型导出为3D PDF格式具有重要的意义。同时,HOOPS Publish作为一个领先的解决方案,为…...

【springboot】闲话 springboot 的几种异步机制 及 长轮询的概念和简单实现
文章目录 引子springboot的几种异步形式开启异步支持和线程池配置(重要)第一种:Async第二种:Callable<T>第三种:WebAsyncTask<T>第四种:DeferredResult<T> 长轮询的简单实现概念实现服务…...

Mysql---安全值守常用语句
文章目录 目录 文章目录 一.用户权限设置 用户设置 元数据查询 Union联合查询 分组查询 字符串函数 总结 一.用户权限设置 用户设置 #用户创建 create user "用户名""%主机名" identified by "密码" #用户删除 drop user 用户名 #用户查询…...

containerd快速安装指南
1 containerd快速安装指南🚀 本指南旨在提供一个简洁有效的方法来安装containerd。我们将通过一份易于理解的脚本步骤,指导您完成安装🔧。请根据您的实际需求,适当调整containerd版本及其相关依赖。 注意事项: 本安装…...

Javascript - 正则表达式相关的一些基础的范例
很久以前的一些学习资料,归档发布; 正则表达式的基础,以HTML代码来示范: <html><head><title></title><script language"javascript">function test(){//从页面要求客户输入一个字符串…...
)
JUC:线程活跃性(死锁、活锁、饥饿)
文章目录 线程活跃性死锁活锁解饿 线程活跃性 死锁 两个线程相互等待对方已拥有的锁,就会相互一直等待,不会停止。 t1拥有a锁,等待b锁。 t2拥有b锁,等待a锁。 Slf4j(topic "c.Test3") public class st3 {public st…...

RGB到灰度图像的转换原理及例程
RGB到灰度图像的转换是一种常用的图像处理操作,其原理是根据人眼对不同颜色的敏感度,将彩色图像的红、绿、蓝三个通道的像素值按照一定权重进行加权平均,得到灰度图像的像素值。 在RGB图像中,每个像素点由红、绿、蓝三个分量组成…...
PCA+DBO+DBSCN聚类,蜣螂优化算法DBO优化DBSCN聚类,适合学习,也适合发paper!
PCADBODBSCN聚类,蜣螂优化算法DBO优化DBSCN聚类,适合学习,也适合发paper! 一、蜣螂优化算法 摘要:受蜣螂滚球、跳舞、觅食、偷窃和繁殖等行为的启发,提出了一种新的基于种群的优化算法(Dung Beetle Optim…...

创建数据库与表单以及管理表单和数据
一、用于创建数据库的命令以及作用 命令作用CREATE DATABASE 数据库名称创建新的数据库DESCRIBE 表单名称描述表单UPDATE 表单名称SET attribute新值WHERE attribute>原始值更新表单中的数据USE 数据库名称指定使用的数据库SHOW databases显示当前已有的数据库SHOW tables显…...

Milvus+ATTU环境搭建
1.使用Docker Compose安装Milvus Standalone 下载安装单机版milvus向量数据库 https://milvus.io/docs/install_standalone-docker.md wget https://github.com/milvus-io/milvus/releases/download/v2.2.12/milvus-standalone-docker-compose.yml -O docker-compose.yml sud…...
Python 基于 OpenCV 视觉图像处理实战 之 OpenCV 简单实战案例 之八 简单水彩画效果
Python 基于 OpenCV 视觉图像处理实战 之 OpenCV 简单实战案例 之八 简单水彩画效果 目录 Python 基于 OpenCV 视觉图像处理实战 之 OpenCV 简单实战案例 之八 简单水彩画效果 一、简单介绍 二、简单图像浮雕效果实现原理 三、简单水彩画效果案例实现简单步骤 四、注意事项…...

Chrome浏览器 安装Vue插件vue-devtools
前言 vue-devtools 是一个为 Vue.js 开发者设计的 Chrome 插件。它可以让你更轻松地审查和调试 Vue 应用程序。与普通的浏览器控制台工具不同,Vue.js devtools 专为 Vue 的响应性数据和组件结构量身定做。 1. 功能介绍 组件树浏览:这个功能可以让你查…...
相册清理大师-手机重复照片整理、垃圾清理软件
相册清理大师是一款超级简单实用的照片视频整理工具。通过便捷的操作手势,帮助你极速整理相册中的照片和视频、释放手机存储空间。 【功能简介】 向上滑动:删除不要的照片 向左滑动:切换下一张照片 向右滑动:返回上一张照片 整理分…...
【GitLab】Ubuntu 22.04 快速安装 GitLab
在 Ubuntu 22.04 上安装最新版本的 GitLab,可以按照以下步骤操作: 1. 更新系统: 在终端中执行以下命令以确保系统是最新的: sudo apt update sudo apt upgrade2. 安装依赖: 安装 GitLab 所需的依赖包: …...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...
