九龙证券|磷酸亚铁锂是什么?磷酸亚铁锂的特点和性能介绍
磷酸亚铁锂是一种新式锂离子电池电极资料,化学式:LiFePO4,磷酸亚铁锂为近来新开发的锂离子电池电极资料,首要用于动力锂离子电池,作为正极活性物质运用,人们习气也称其为磷酸铁锂。
磷酸亚铁锂的特色和功能
1、高能量密度:其理论比容量为170mAh/g,产品实践比容量已超过150 mAh/g(0.2C, 25°C);
2、安全性:是现在最安全的锂离子电池正极资料;并且不含任何对人体有害的重金属元素。
3、寿数长:在100%DOD条件下,能够充放电2000次以上,这是原因磷酸铁锂晶格稳定性好,锂离子的嵌入和脱出对晶格的影响不大,故而具有良好的可逆性。存在的缺乏是电子离子传到率差,不适宜大电流的充放电。为了将其应用到电动车和电动工具上,人们在资料的表面包覆导电资料(首要是碳)、掺杂其他金属氧化物取代部分Fe的晶格位置,现已使磷酸亚铁锂的导电性提高了100万倍以上。现在,该资料制成的锂离子电池,能够进行10--20C甚至30C的大电流放电和充电,并且放电功能优良。)
4、无回忆效应;
5、电功能,磷酸亚铁锂正极资料的锂电池,能够运用大倍率充电,现在最快可在30分钟内将电池充溢。
详细的物理参数:(1)松装密度:0.8g/cm,(2)振实密度:1.1--1.4g/cm,(3)中位粒径:2.0--5.0um,(4)比表面积<15m/g,(5)涂片参数:LiFePo4:C:PVDF=90:3:7,(6)极片压实密度:2.1-2.4g/cm
电化功能:克容量>150mAh/g ,测验条件:半电池:0.2C,4--2.0V,大于154mAh;根据实践电池0.2C放电,放电电压:3.65V--2.5V,温度25℃,放电容量大于150mAh。
6、循环次数2000次
锂离子电池的功能首要取决于正负极资料,磷酸亚铁锂作为锂离子电池的正极资料是近几年才出现的事,国内开宣布大容量磷酸亚铁锂电池是2005年7月。其安全功能与循环寿数是其它资料所无法比较的,这些也正是动力电池最重要的技术指标。1CDOD充放循环寿数达2000次。单节电池过充电压30V不燃烧,穿刺不爆炸。
磷酸亚铁锂正极资料能够做成更大容量锂离子电池,更易串联运用,以满足电动车频繁充放电的需要,其无毒、无污染、安全功能好、原资料来历广泛、价格便宜,寿数长等优点,是新一代锂离子电池的理想正极资料。
相关文章:

九龙证券|磷酸亚铁锂是什么?磷酸亚铁锂的特点和性能介绍
磷酸亚铁锂是一种新式锂离子电池电极资料,化学式:LiFePO4,磷酸亚铁锂为近来新开发的锂离子电池电极资料,首要用于动力锂离子电池,作为正极活性物质运用,人们习气也称其为磷酸铁锂。 磷酸亚铁锂的特色和功能…...
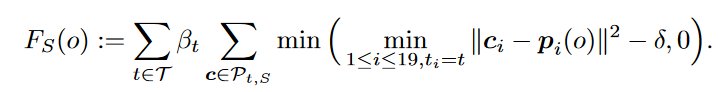
3D目标检测(二)—— 直接处理点云的3D目标检测网络VoteNet、H3DNet
前言上次介绍了基于Point-Based方法处理点云的模块,3D目标检测(一)—— 基于Point-Based方法的PointNet点云处理系列,其中相关的模块则是构成本次要介绍的,直接在点云的基础上进行3D目标检测网络的基础。VoteNet对于直接在点云上预…...
)
Java学习-IO流-常用工具包(hutool)
Java学习-IO流-常用工具包(hutool) hutool工具包 DateUtil:日期时间工具类 TImeInterval:计时器工具类 StrUtil:字符串工具类 HexUtil:16进制工具类 HashUtil:Hash算法类 ObjectUtil࿱…...

【LeetCode】1. 两数之和
题目链接:https://leetcode.cn/problems/two-sum/ 📕题目要求: 给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。 你可以假设每种输入…...

【数值模型环境搭建】Intel编译器安装
Intel编译器在数值模型编译中被广泛使用,它有一个很好的地方是自带Mpich,不需要额外安装。本文介绍Intel2018.1.163版本的安装。 1、安装包获取 Intel编译器可从官网下载下载: https://www.intel.cn/content/www/cn/zh/homepage.html 或者…...

操作VMware vCenter Converter 实现物理机迁移到虚拟机
实验目的:熟练VMware虚拟化项目中,物理机向ESXI5迁移操作过程。 1、打开VMwarevCenterConverterStandalone5.0软件,按“转换计算机”。 2、选择“已打开电源的计算机”。并输入远程要连接迁移物理机IP地址,登录帐户和密码。 然后…...
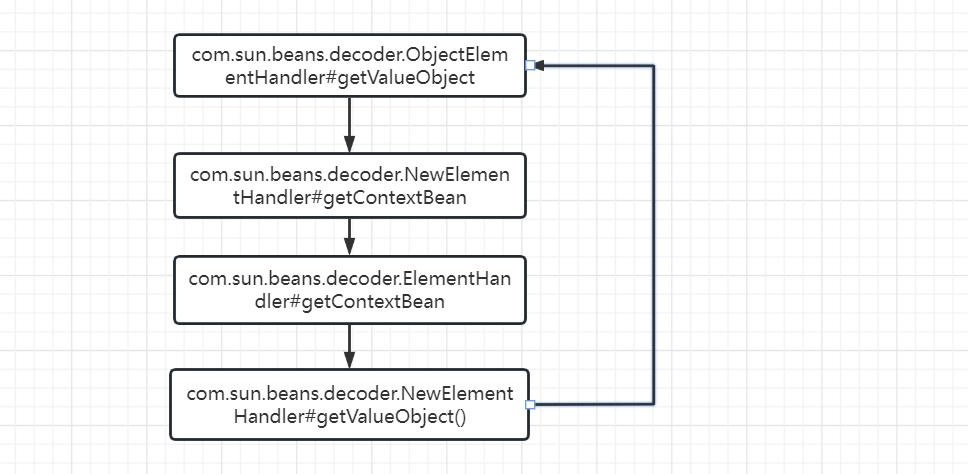
hutool XML反序列化漏洞(CVE-2023-24162)
漏洞简介 Hutool 中的XmlUtil.readObjectFromXml方法直接封装调用XMLDecoder.readObject解析xml数据,当使用 readObjectFromXml 去处理恶意的 XML 字符串时会造成任意代码执行。 漏洞复现 我们在 maven 仓库中查找 Hutool https://mvnrepository.com/search?…...

Java简单认识泛型——图文详解
写在开头:想必大家和博主一样,在以往学习JavaSE的语法中,遇到了一个陌生的词——泛型,博主当时很好奇,什么是泛型呢?即使是学完了JavaSE,这个问题都没有解决,只能在百度查阅了解关于泛型的一些皮…...

AcWing171.送礼物
题目描述 达达帮翰翰给女生送礼物,翰翰一共准备了NNN 个礼物,其中第 iii 个礼物的重量是 G[i]G[i]G[i]。 达达的力气很大,他一次可以搬动重量之和不超过 WWW 的任意多个物品。 达达希望一次搬掉尽量重的一些物品,请你告诉达达在…...
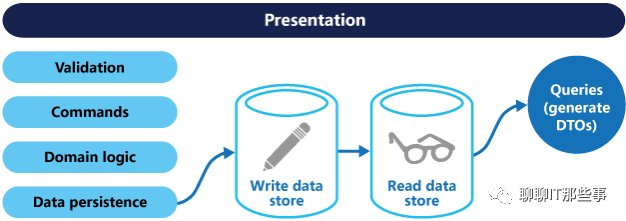
领域驱动设计-架构篇
目录 1、软件架构概述 1.1 软件架构概念 1.2 软件架构分类 1.3 软件架构模式 1.4 软件架构风格 2、领域驱动软件架构 2.1 架构风格 六边行架构(领域驱动设计首选) 为什么选择REST架构 松耦合 可伸缩性 易用性 约束性 2.2 架构模型 命令和…...

docker安装kafka
前言最近在用kafka做项目,所以本地搭建下kafka,但是又嫌java安装和安装kafka太麻烦,所以想到用docker来部署。镜像wurstmeister/kafka维护较为频繁的一个Kafka镜像。只包含了Kafka,因此需要另行提供ZooKeeper,推荐使用…...
 - Page Factory设计模式)
Selenium4+Python3系列(十一) - Page Factory设计模式
写在前面: Page Object模式,目的是将元素定位和元素操作分层,只接触测试内容,不写基础内容,便于后续对自动化测试用例体系的维护,这是中心思想,也是核心。 那么我们继续将简洁延续,…...

C++基础知识【4】函数及参数
目录 一、函数的基本概念 1.1、构成 1.2、声明和定义 1.3、函数的调用 二、参数 2.1、形参和实参 2.2、参数的传递 传值 传引用 传指针 三、C函数的一些新特性 3.1、Lambda表达式 3.2、右值引用 3.3、默认参数 3.4、变长参数模板 3.5、constexpr函数 3.6、noex…...

约瑟夫森磁效应
电流与波函数的相位有直接的关系,可得约瑟夫森结的电流为 IIcsinϕ\begin{align} II_c sin\phi \end{align} IIcsinϕ 式中,IcI_cIc为临界电流,相位差为ϕϕ2−ϕ1\phi\phi_2-\phi_1ϕϕ2−ϕ1。 根据磁矢势A的定义,B…...
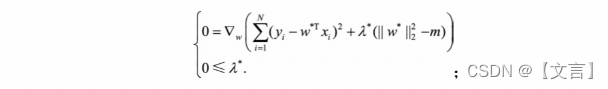
什么是L1和L2正则化,以及它们有什么区别
一、L1和L2正则化是什么? 在防止过拟合的方法中有L1正则化和L2正则化,L1和L2是正则化项,又叫做惩罚项,是为了限制模型的参数,防止模型过拟合而加在损失函数后面的一项。 在二维的情况下,黄色的部分是L2和…...
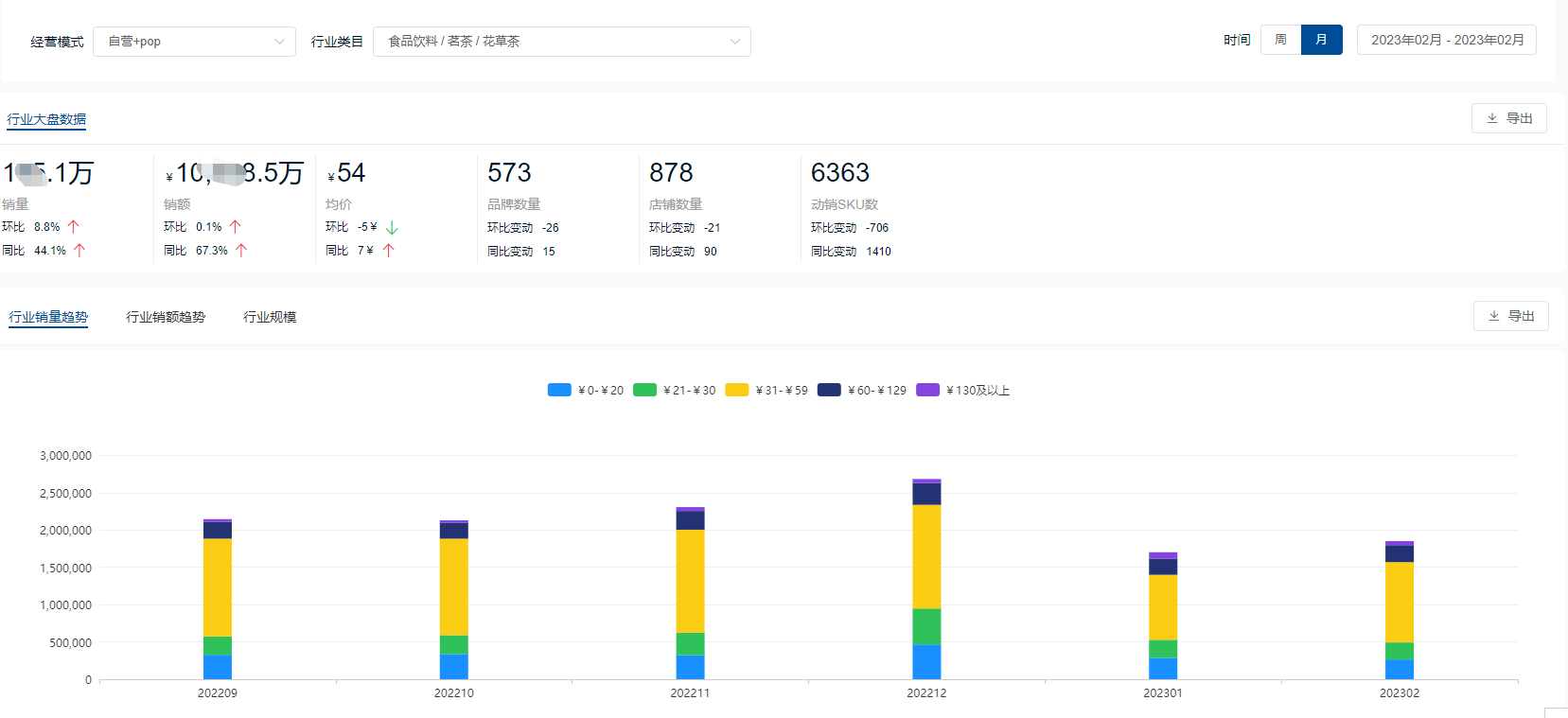
场景式消费激发春日经济,这些电商品类迎来消费热潮
春日越临近,商机越浓郁。随着气温渐升,春日经济已经潜伏在大众身边。“春菜”、“春装”、“春游”、“春季养生”等春日场景式消费走热。 下面,鲸参谋为大家盘点几个与春日经济紧密相关的行业。 •春日仪式之春游踏青 ——户外装备全面开花…...
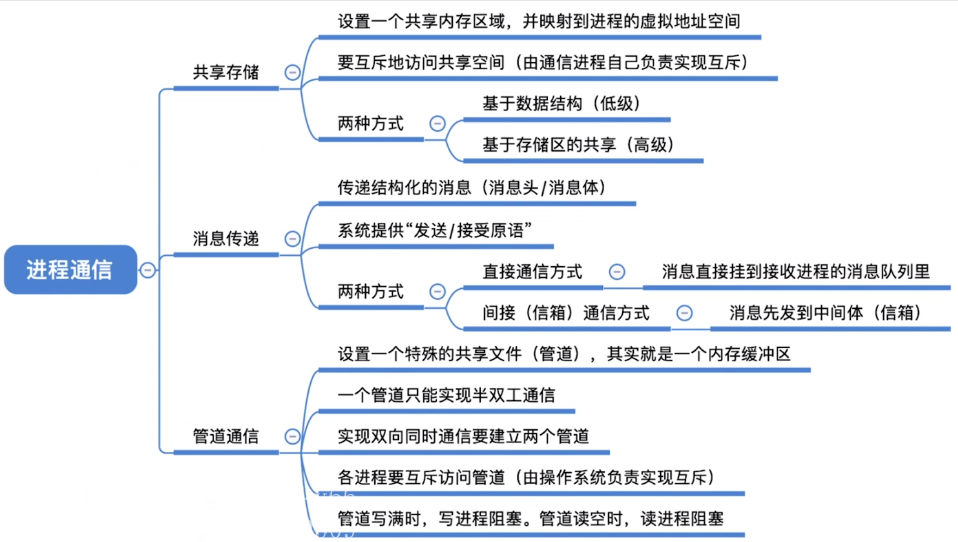
[2.1.4]进程管理——进程通信
文章目录第二章 进程管理进程通信(IPC)为什么进程通信需要操作系统支持?(一)共享存储(1)基于存储区的共享(2)基于数据结构的共享(二)消息传递什么…...

ChatGPT也有犯晕的时候
前面测试 ChatGPT 进行写代码、优化代码、解释代码、一般问答都表现的很好。偷个懒,用ChatGPT 帮我写段生物信息代码如果 ChatGPT 给出的的代码不太完善,如何请他一步步改好?代码看不懂?ChatGPT 帮你解释,详细到爆&…...

机器学习与目标检测作业:连通块算法
机器学习与目标检测作业:连通块算法一、连通块算法题目描述二、连通块算法文件结构三、连通块算法程序编写3.1、连通块算法conBlock.h头文件内容3.2、conBlock.cpp源文件内容3.3.3、mian.h头文件内容3.3.4、main.cpp源文件内容如下四、连通块算法程序运行结果一、连…...

HBase基础 --- 增删查改
目录 创建表 查看指定表全名空间中的表 查看表描述 禁用/启用 查看禁用/启动状态 删除表 新增列族 删除列族 更改列族存储版本的限制 增加数据 根据条件查询 查看指定列中不同版本的数据 删除指定列族下的指定列 删除指定行 全表扫描 全表扫描指定列族…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...
