每日一题 --- 三数之和[力扣][Go]
三数之和
题目:15. 三数之和
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。请
你返回所有和为 0 且不重复的三元组。
**注意:**答案中不可以包含重复的三元组。
示例 1:
输入:nums = [-1,0,1,2,-1,-4]
输出:[[-1,-1,2],[-1,0,1]]
解释:
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意,输出的顺序和三元组的顺序并不重要。
示例 2:
输入:nums = [0,1,1]
输出:[]
解释:唯一可能的三元组和不为 0 。
示例 3:
输入:nums = [0,0,0]
输出:[[0,0,0]]
解释:唯一可能的三元组和为 0 。
提示:
3 <= nums.length <= 3000-105 <= nums[i] <= 105
方法:
先排序,三个数,先固定一个不动指向的数为n,使用双指针,在不动的数下标到数组中间的数中找到两个指向数的结果为-n的数。注意指针滑动过程中一定要跳过所有与前一位数相同的数。
func threeSum(nums []int) [][]int {res := make([][]int, 0)Len := len(nums)qSort383(nums, 0, Len-1)for i := 0; i < Len; {l, r := i+1, Len-1for l < r {if nums[i]+nums[l]+nums[r] < 0 {l++for l < r && nums[l] == nums[l-1] {l++}} else if nums[i]+nums[l]+nums[r] > 0 {r--for l < r && nums[r+1] == nums[r] {r--}} else {res = append(res, []int{nums[i], nums[l], nums[r]})l++for l < r && nums[l] == nums[l-1] {l++}r--for l < r && nums[r+1] == nums[r] {r--}}}i++for i < Len && nums[i] == nums[i-1] {i++}}return res
}func qSort383(nums []int, low, high int) {if low >= high {return}pos := position383(nums, low, high)qSort383(nums, low, pos-1)qSort383(nums, pos+1, high)
}func position383(nums []int, low, high int) int {base := nums[low]l, r := low, highfor l < r {for l < r && nums[r] >= base {r--}nums[l] = nums[r]for l < r && nums[l] <= base {l++}nums[r] = nums[l]}nums[l] = basereturn l
}
相关文章:

每日一题 --- 三数之和[力扣][Go]
三数之和 题目:15. 三数之和 给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i ! j、i ! k 且 j ! k ,同时还满足 nums[i] nums[j] nums[k] 0 。请 你返回所有和为 0 且不重复的三元组。 **注意&#x…...
)
vue render 函数详解 (配参数详解)
vue render 函数详解 (配参数详解) 在 Vue 3 中,render 函数被用来代替 Vue 2 中的模板语法。 它接收一个 h 函数(或者是 createElement 函数的别名),并且返回一个虚拟 DOM。 render 函数的语法结构如下: render(h) …...
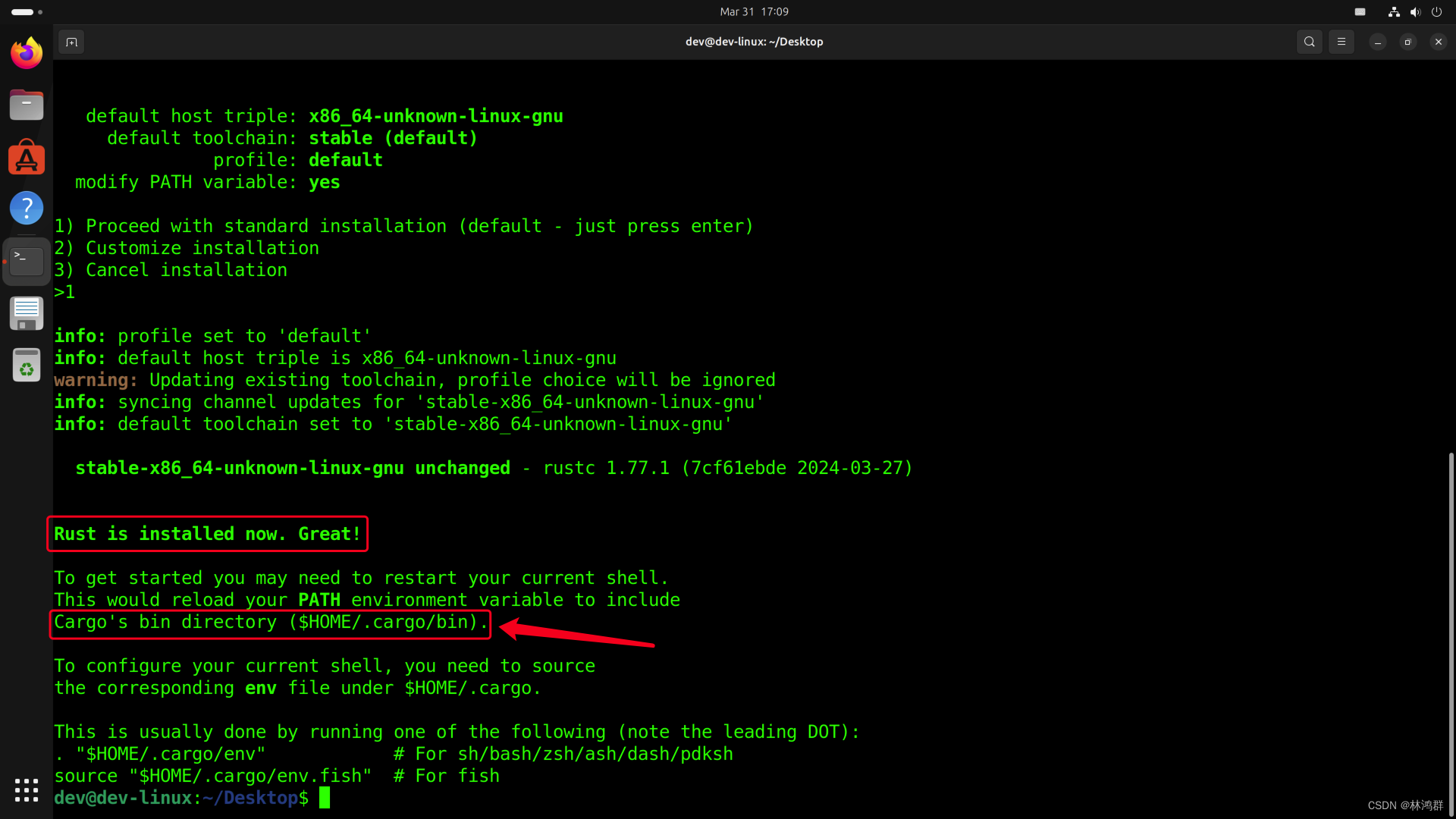
ubuntu23.10配置RUST开发环境
系统版本: gcc版本 下载rustup安装脚本: curl --proto =https --tlsv1.2 https://sh.rustup.rs -sSf | sh下载完成后会自动执行 选择默认安装选项 添加cargo安装目录到环境变量 vim ~/.bashrc<...

Vue性能优化--gZip
一、gZip简单介绍 1.1 什么是gzip gzip是GNUzip的缩写,最早用于UNIX系统的文件压缩。HTTP协议上的gzip编码是一种用来改进web应用程序性能的技术,web服务器和客户端(浏览器)必须共同支持gzip。目前主流的浏览器,Chro…...

蓝桥杯第七届大学B组详解
目录 1.煤球数量; 2.生日蜡烛; 3.凑算式 4.方格填数 5.四平方和 6.交换瓶子 7.最大比例 1.煤球数量 题目解析:可以根据题目的意思,找到规律。 1 *- 1个 2 *** 3个 3 ****** 6个 4 ********** 10个 不难发现 第…...

荣誉 | 人大金仓连续三年入选“金融信创优秀解决方案”
3月28日,由中国人民银行领导,中国金融电子化集团有限公司牵头组建的金融信创生态实验室发布“第三期金融信创优秀解决方案”,人大金仓新一代手机银行系统解决方案成功入选,这也是人大金仓金融行业解决方案连续第三年获得用户认可。…...
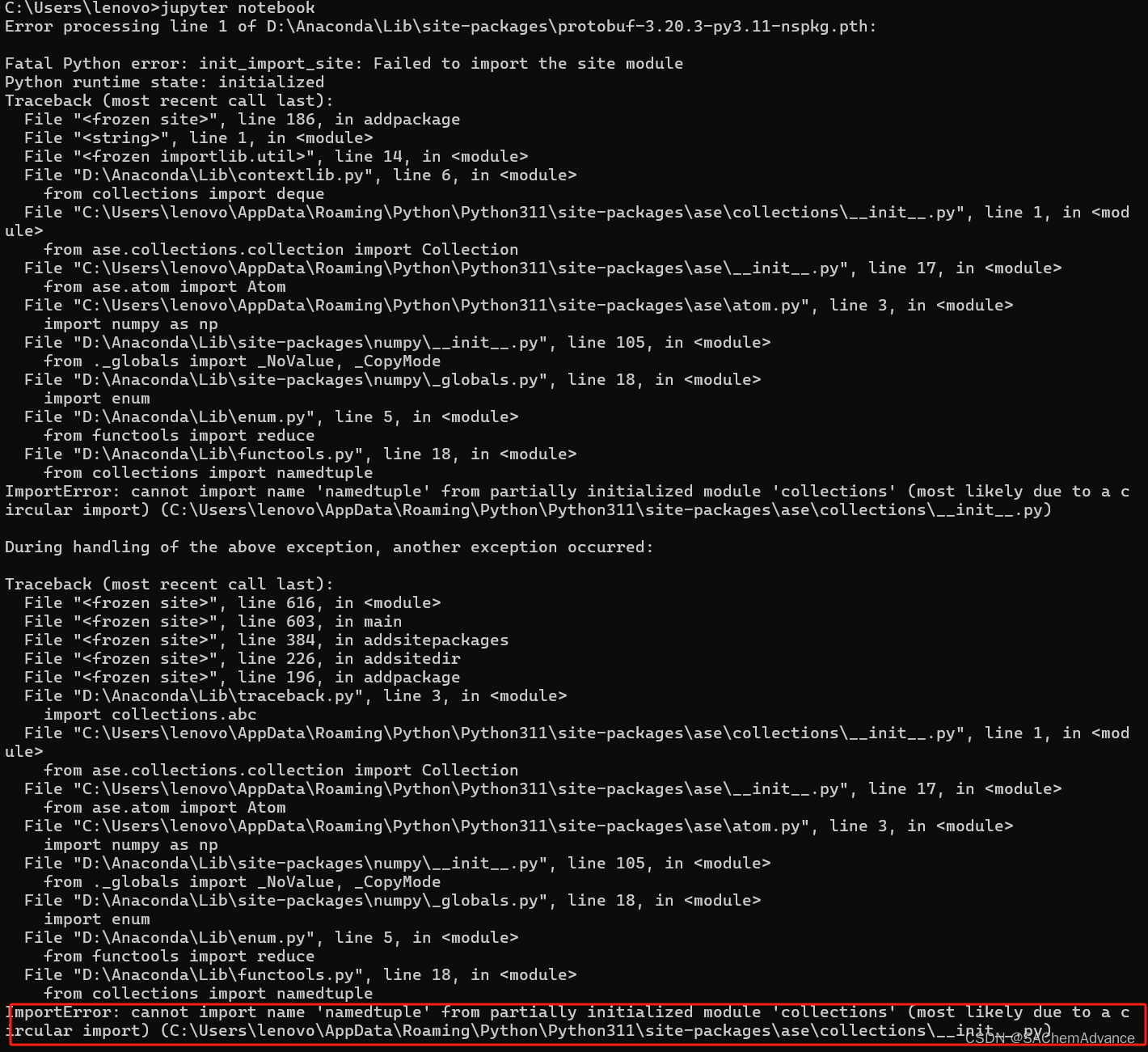
【关于jupyter notebook】一打开就闪退的问题
在Anaconda Prompt中输入jupyter notebook发现是有个错误。 里面多了一个__init__.py的文件导致报错。删除之后,就可以使用了...
若依 3.8.7版本springboot前后端分离 整合mabatis plus
1.去掉mybatis 这一步我没有操作,看别人的博客有说不去掉可能冲突,也可能不冲突,我试下来就没去掉如需要去除,到总的pom.xml中properties标签下的<mybatis-spring-boot.version>x.x.x</mybatis-spring-boot.version>…...

vue做移动端自适应插件实现rem
1.实现方式 postcss-pxtorem:将px转换为rem amfe-flexible:为html、body提那家font-size,窗口调整的时候重新设置font-size 2.安装与使用 npm install amfe-flexible --save npm install postcss-pxtorem --save-dev 1.再main.js入口文件…...
)
android 快速实现 图片获取并裁剪(更换头像)
1.获取图片框架:https://github.com/LuckSiege/PictureSelector 2.图片裁剪框架:https://github.com/jdamcd/android-crop 3.Glide图片加载框架:https://github.com/bumptech/glide 2.build.gradle依赖: dependencies {// Pic…...

垃圾回收机制--GC 垃圾收集器--JVM调优-面试题
1.触发垃圾回收的条件 新生代 Eden区域满了,触发young gc (ygc)老年代区域满了,触发full gc (fgc)通过ygc后进入老年代的平均大小大于老年代的可用内存,触发full gc(fgc).程序中主动调用的System.gc()强制执行gc,是full gc,但是不必然执行。…...
)
Java基础知识总结(29)
Java虚拟机 运行时数据区 程序计数器 方法区:Java 8以后没有方法区,改为了元空间(MetaSpace) 虚拟机栈 堆 本地方法栈 程序计数器 它可以看作是当前线程所执行的字节码的行号指示器。在Java虚拟机的概念模型里,…...

vue js金额转中文
在Vue.js项目中,实现金额转中文的功能通常涉及编写一个JavaScript方法来处理数字转换逻辑,并在Vue组件中调用该方法。下面是一个基本的示例,展示如何在Vue组件中定义一个计算属性或方法来实现这一功能: /*** 思路: …...
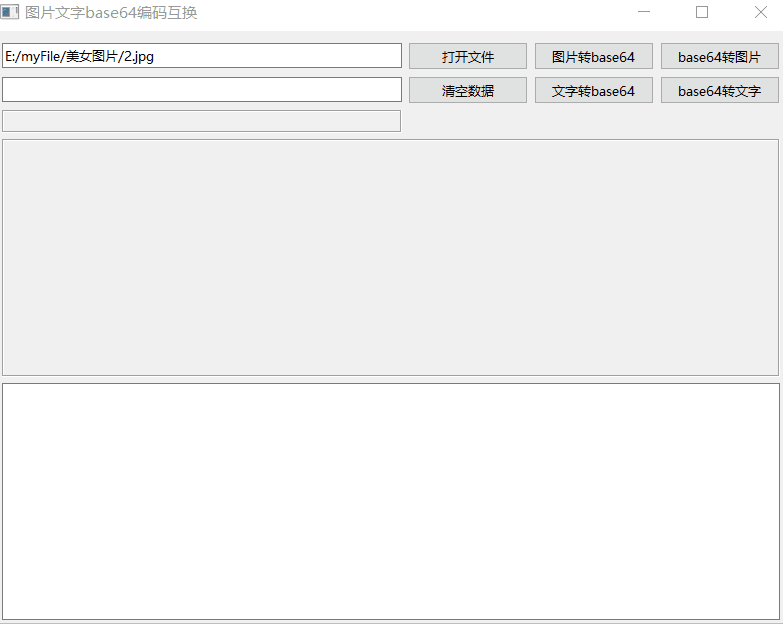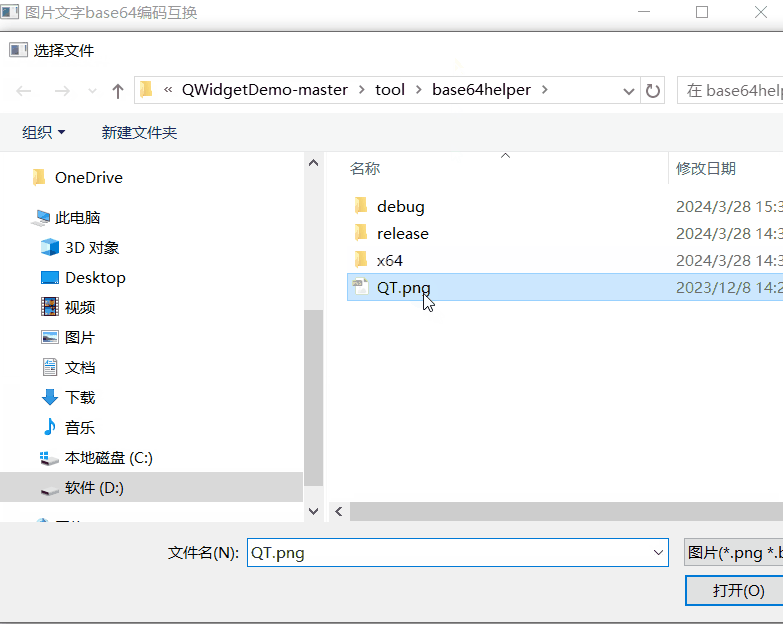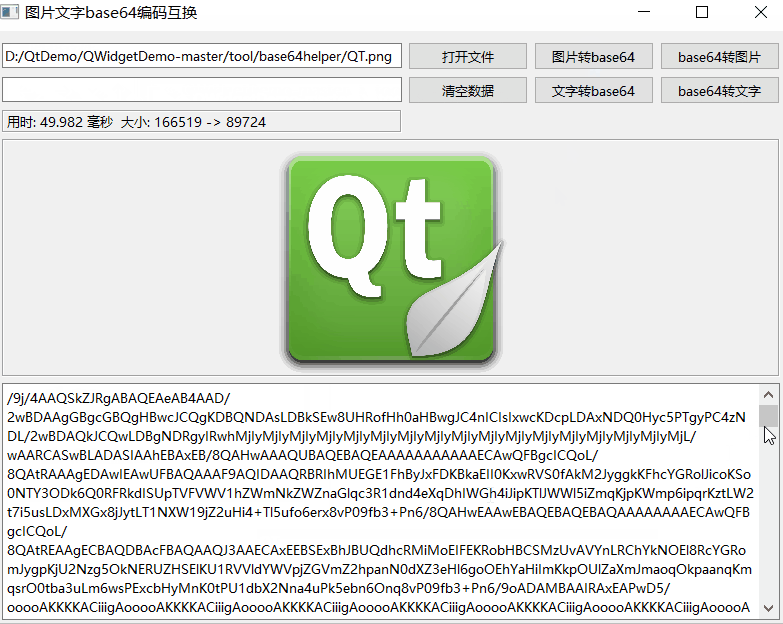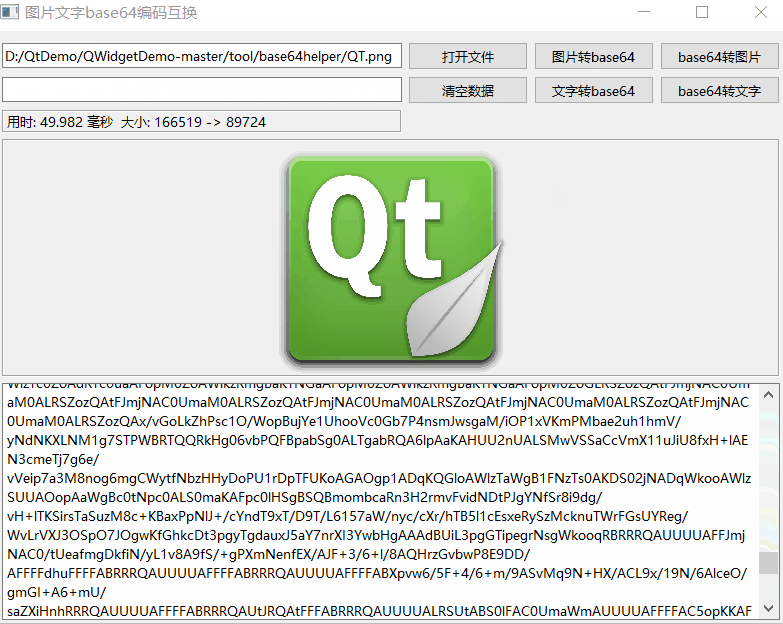
《QT实用小工具·二》图片文字转base64编码
1、概述 源码放在文章末尾 base64编码转换类 图片转base64字符串。base64字符串转图片。字符转base64字符串。base64字符串转字符。后期增加数据压缩。Qt6对base64编码转换进行了重写效率提升至少200%。 下面是demo演示: 项目部分代码如下所示: #ifn…...
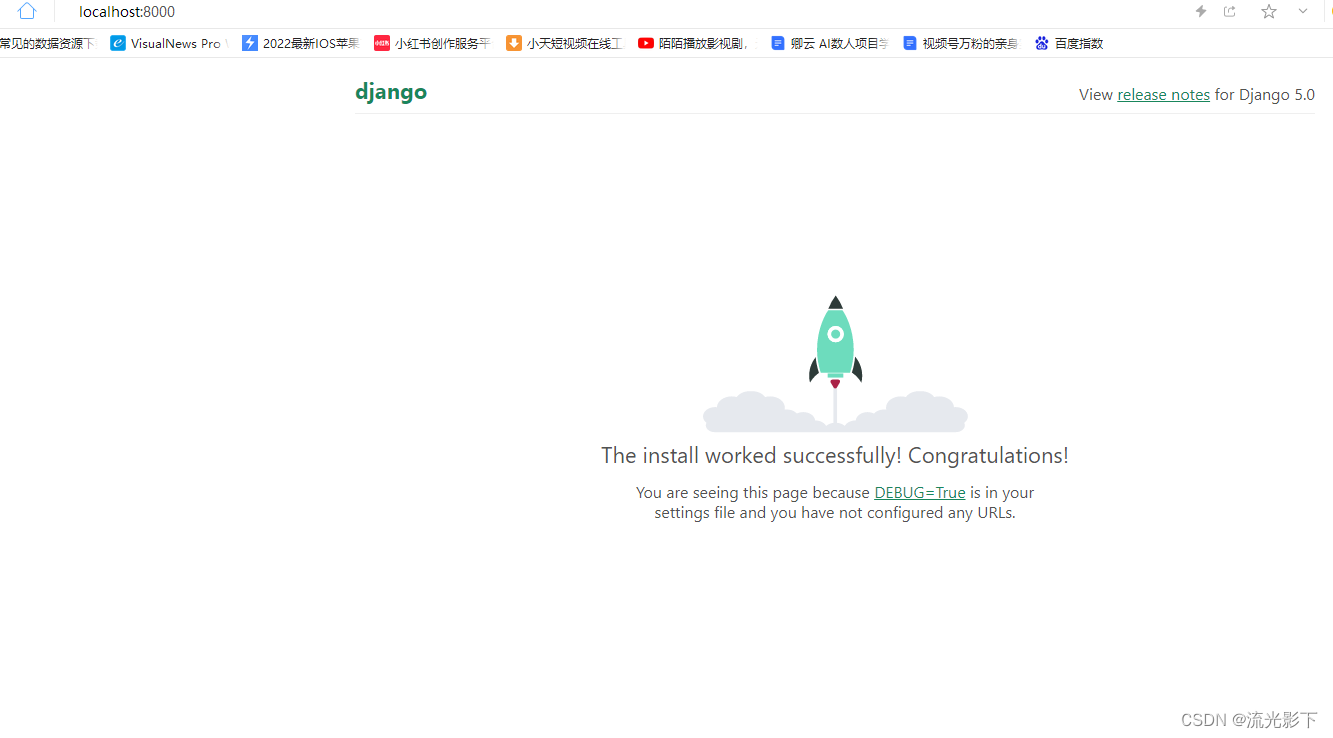
Django安装及第一个项目
1、安装python C:\Users\leell>py --version Python 3.10.6 可以看出我的环境python的版本3.10.6,比较新 2、 Python 虚拟环境创建 2.1 官网教程 目前,有两种常用工具可用于创建 Python 虚拟环境: venv 在 Python 3.3 及更高版本中默…...

专升本-物联网
物联网(IOT,Internet of things) 体系结构: 感知层(感知执行层) 网络层 应用层 基本特征: 全面感知 可靠传输 智能处理 作用: 信息采集、转换、收集 信息传递和处理 数据…...

二叉树的遍历C语言
二叉树作为FDS课程最核心的数据结构之一,要求每个人都掌握! 这是一道简单的二叉树问题! 我们将给出一颗二叉树,请你输出它的三种遍历,分别是先序遍历,中序遍历,后序遍历! 输入格式…...
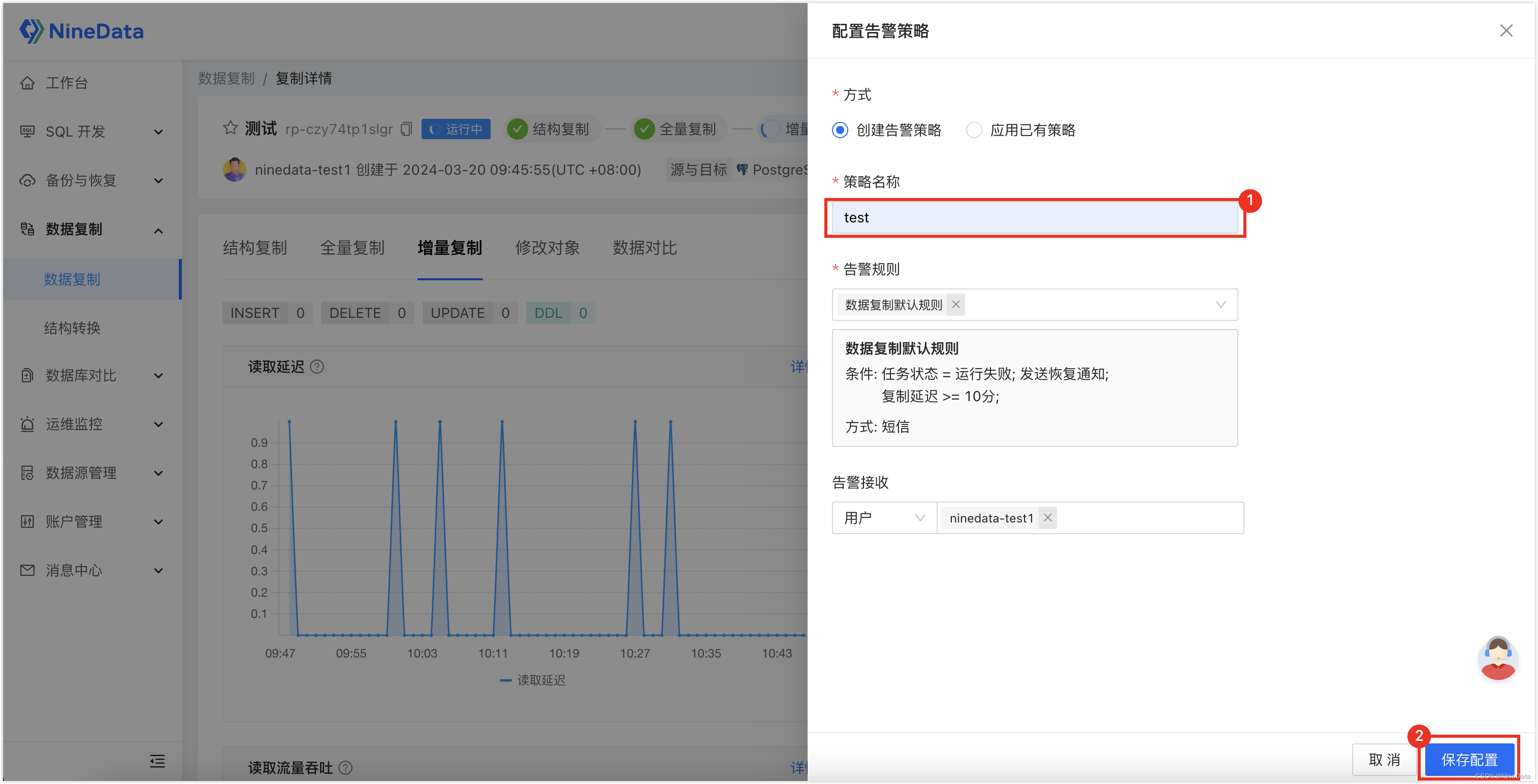
PostgreSQL到Doris的迁移技巧:实时数据同步新选择!
PostgreSQL可以说是目前比较抢手的关系型数据库了,除了兼具多样功能和强大性能之外,还具备非常优秀的可扩展性,更重要的是它还开源,能火不是没有理由的。 虽然PostgreSQL很强大,但是它也有短板,相对于专业…...
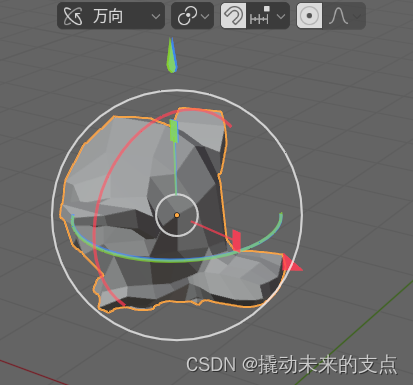
【三维】关于万向节锁的直白解释
1. 分析理解 万向节长什么样子,请参考这篇文章中的图片:https://zhuanlan.zhihu.com/p/42519819。 看了很多篇解释性的文章,没怎么看懂。因为我个人最关注的问题点在于: 现实物体旋转为什么没有所谓的万向节锁的bug,…...

程序员的修养 - 变量
变量几乎代码程序程序 中最基础的组成单元,程序员几乎无时无刻都在接触变量。但你对变量的理解真的足够吗? 首先,什么是变量?! 第一层理解:一个可以改变的量,区别于常量,用户可以修…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...
