蓝桥杯刷题第四天



思路:
这道题很容易即可发现就是简单的暴力即可完成题目,我们只需满足所有数的和为偶数即可保证有满足条件的分法,同时也不需要存下每个输入的数据,只需要知道他是偶数还是奇数即可,因为我们只需要偶数个奇数搭配在一块看成是偶数即可,然后对应到上面我们就可以统计一组数据中奇数的个数就不需要多余的计算一个数据和,当奇数个数为0时,情况就是取和不取问题组合情况为2的偶数的个数次方,当奇数个数为奇数时,必不可能有满足条件的情况,当奇数个数为偶数且不为0时,每两个奇数即可配合成一个偶数,奇数的组合数为2的(奇数的个数-1)次方。ps:可以理解为先取出一个奇数,其余奇数为取或者不取那么其中一个子集有奇数个数的奇数另一个必有偶数个数的奇数,只需把这些排列组合(有2的(奇数的个数-1)次方种情况)列出并把取出的奇数放到只有奇数个数的奇数那个子集即可满足条件。
还有说因为奇数得成对出现所以2的n次方除2这个我理解不了我个人想法写到了上面的ps上
核心代码段:

代码:
import java.util.*;public class Main {public static void main (String []args) {int T;Scanner a = new Scanner(System.in);T=a.nextInt();int sum[] = new int[T];int n1=T;while(T-->0){int n;n = a.nextInt();//统计数量int b;//统计奇数和偶数的数目int nj,no;nj=no=0;for(int i=0;i<n;i++) {b=a.nextInt();if(b%2==0) {++no;}else {++nj;}}if(nj%2==0) {//将两个奇数合并为一个偶数,而n个奇数共有n-1种组合然后就是排列组合问题了最多有2的n次方种情况int num =nj+no;if(nj!=0) {num--; }sum[T]=1;
// for(int i=0;i<num;i++) {
// sum[T]=sum[T]*2%1000000007;
// }sum[T]=(int) (Math.pow(2,num)%1000000007);}else {sum[T]=0;} }a.close();for(T=n1-1;T>=0;T--) {System.out.println(sum[T]);}}
}做题反思:
1.蜜汁报错
蓝桥杯代码执行结果为段错误即有越界行为
2.题目有多组数据要输出下面两种都是可以的1.把数据存下来然后一起输出2.算出一个就输出。

fig:情况1
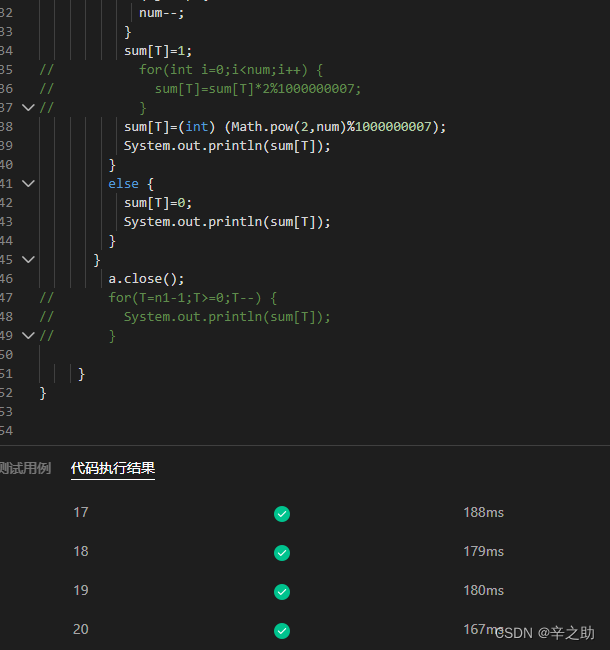
fig:情况2
3.pow返回值为double,先进行(int)会导致精度受损,固要先取余(蓝桥杯很多时候都要先取余输出低位的数值)再数据转换。

eg:
sum[T]=(int) (Math.pow(2,nj)%1000000007);和
sum[T]=(int) Math.pow(2,nj)%1000000007;
的区别在第一个是先取余再转int精度没有丢失,后者是先转int再取余精度在大范围数的时候double变int会精度丢失导致在数值比较大的情况下二者的计算结果有所区别。
上者可以20个结果都对,后者只对4个结果(数据范围小没损失精度)
前者:

后者:
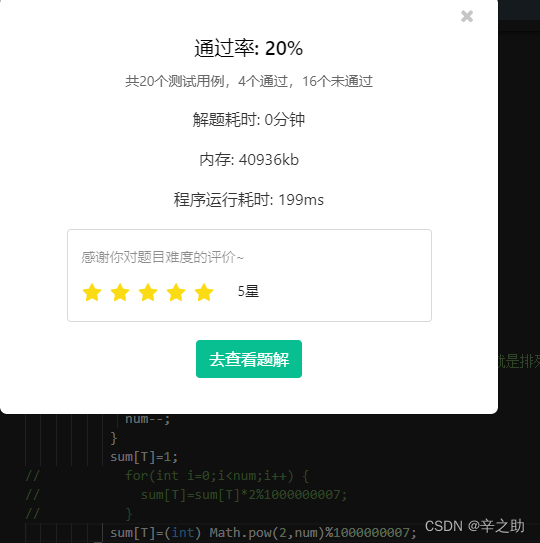
4.区分好continue和break的区别
continue是结束该轮循环,但并没有跳出
break是结束循环即跳出循环

我一开始直接这样导致一直找不到问题,因为就是遇到不满足情况的就跳出循环了,后面的组使用都没有去做,有点逆天了,敲得还是太少了
代码其实十几分钟就敲完了但一直没找出来问题,从晚上7.30到9.20才真正把这道题写完有点ass了
官网一个我觉得写得比较简洁的版本(内核是差不多的我进行了模仿去debug上面的代码而已):
import java.util.*;public class Main {public static void main (String []args) {int T;Scanner a = new Scanner(System.in);T=a.nextInt();long sum[] = new long[T];int n1=T;while(T-->0){int n;n = a.nextInt();//统计数量int b;//统计奇数和偶数的数目int nj,no;nj=no=0;for (int j = 0; j < n; ++j) {int e = a.nextInt();if (e % 2 == 0) ++no;else ++nj;}if (nj % 2 == 0)sum[T] = (int) (Math.pow(2, no) * Math.pow(2, nj == 0 ? 0 : nj - 1) % 1000000007);else sum[T] = 0;}a.close();for(T=n1-1;T>=0;T--) {System.out.println(sum[T]);}}
}相关文章:

蓝桥杯刷题第四天
思路: 这道题很容易即可发现就是简单的暴力即可完成题目,我们只需满足所有数的和为偶数即可保证有满足条件的分法,同时也不需要存下每个输入的数据,只需要知道他是偶数还是奇数即可,因为我们只需要偶数个奇数搭配在一块…...

03-数据库的用户管理
一、创建新用户 mysql> create user xjzw10.0.0.% identified by 1; Query OK, 0 rows affected (0.01 sec) 二、查看当前数据库正在登录的用户 mysql> select user(); ---------------- | user() | ---------------- | rootlocalhost | ---------------- 1 row …...

每日一题 --- 三数之和[力扣][Go]
三数之和 题目:15. 三数之和 给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i ! j、i ! k 且 j ! k ,同时还满足 nums[i] nums[j] nums[k] 0 。请 你返回所有和为 0 且不重复的三元组。 **注意&#x…...
)
vue render 函数详解 (配参数详解)
vue render 函数详解 (配参数详解) 在 Vue 3 中,render 函数被用来代替 Vue 2 中的模板语法。 它接收一个 h 函数(或者是 createElement 函数的别名),并且返回一个虚拟 DOM。 render 函数的语法结构如下: render(h) …...
ubuntu23.10配置RUST开发环境
系统版本: gcc版本 下载rustup安装脚本: curl --proto =https --tlsv1.2 https://sh.rustup.rs -sSf | sh下载完成后会自动执行 选择默认安装选项 添加cargo安装目录到环境变量 vim ~/.bashrc<...

Vue性能优化--gZip
一、gZip简单介绍 1.1 什么是gzip gzip是GNUzip的缩写,最早用于UNIX系统的文件压缩。HTTP协议上的gzip编码是一种用来改进web应用程序性能的技术,web服务器和客户端(浏览器)必须共同支持gzip。目前主流的浏览器,Chro…...

蓝桥杯第七届大学B组详解
目录 1.煤球数量; 2.生日蜡烛; 3.凑算式 4.方格填数 5.四平方和 6.交换瓶子 7.最大比例 1.煤球数量 题目解析:可以根据题目的意思,找到规律。 1 *- 1个 2 *** 3个 3 ****** 6个 4 ********** 10个 不难发现 第…...

荣誉 | 人大金仓连续三年入选“金融信创优秀解决方案”
3月28日,由中国人民银行领导,中国金融电子化集团有限公司牵头组建的金融信创生态实验室发布“第三期金融信创优秀解决方案”,人大金仓新一代手机银行系统解决方案成功入选,这也是人大金仓金融行业解决方案连续第三年获得用户认可。…...
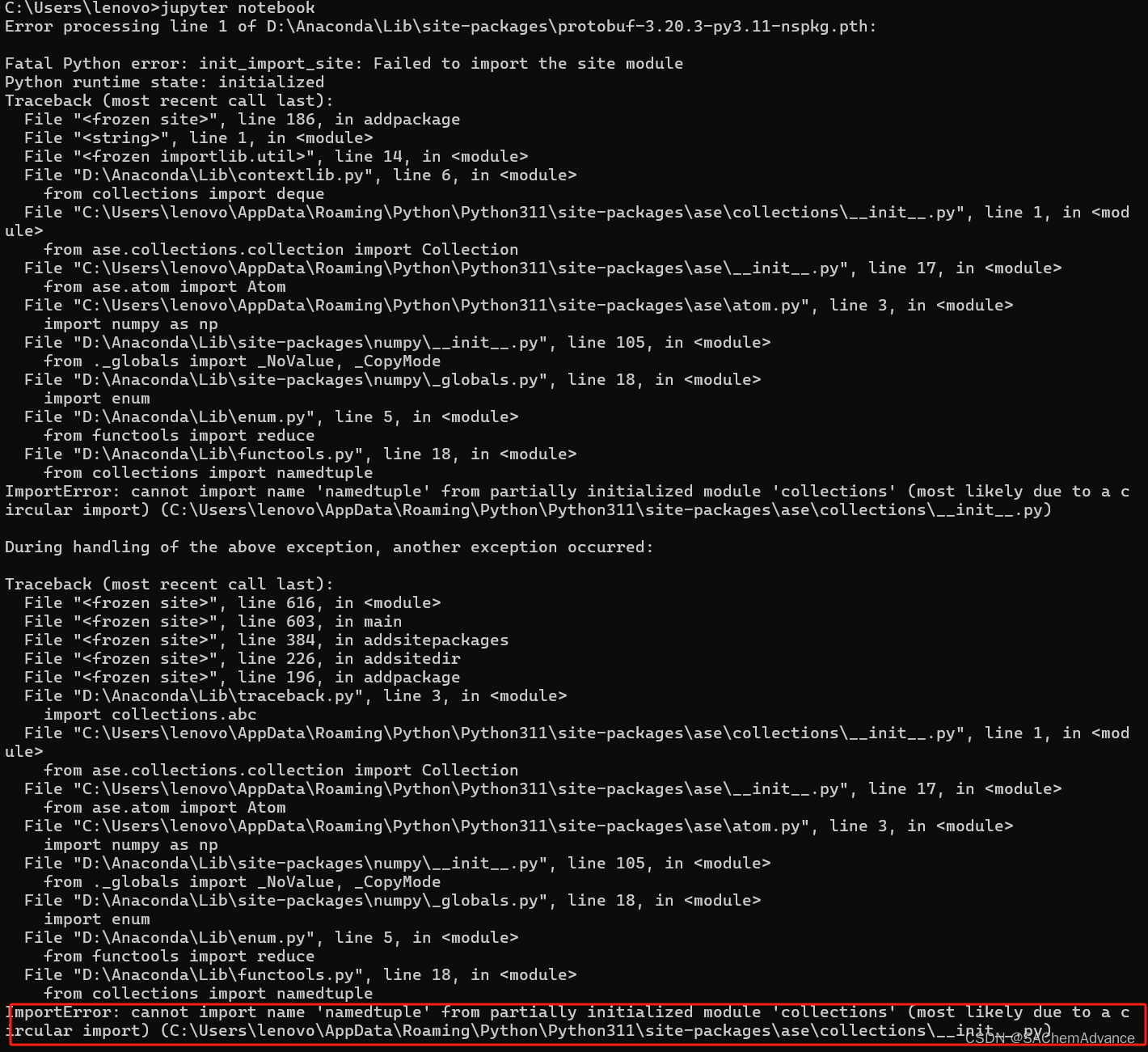
【关于jupyter notebook】一打开就闪退的问题
在Anaconda Prompt中输入jupyter notebook发现是有个错误。 里面多了一个__init__.py的文件导致报错。删除之后,就可以使用了...
若依 3.8.7版本springboot前后端分离 整合mabatis plus
1.去掉mybatis 这一步我没有操作,看别人的博客有说不去掉可能冲突,也可能不冲突,我试下来就没去掉如需要去除,到总的pom.xml中properties标签下的<mybatis-spring-boot.version>x.x.x</mybatis-spring-boot.version>…...

vue做移动端自适应插件实现rem
1.实现方式 postcss-pxtorem:将px转换为rem amfe-flexible:为html、body提那家font-size,窗口调整的时候重新设置font-size 2.安装与使用 npm install amfe-flexible --save npm install postcss-pxtorem --save-dev 1.再main.js入口文件…...
)
android 快速实现 图片获取并裁剪(更换头像)
1.获取图片框架:https://github.com/LuckSiege/PictureSelector 2.图片裁剪框架:https://github.com/jdamcd/android-crop 3.Glide图片加载框架:https://github.com/bumptech/glide 2.build.gradle依赖: dependencies {// Pic…...

垃圾回收机制--GC 垃圾收集器--JVM调优-面试题
1.触发垃圾回收的条件 新生代 Eden区域满了,触发young gc (ygc)老年代区域满了,触发full gc (fgc)通过ygc后进入老年代的平均大小大于老年代的可用内存,触发full gc(fgc).程序中主动调用的System.gc()强制执行gc,是full gc,但是不必然执行。…...
)
Java基础知识总结(29)
Java虚拟机 运行时数据区 程序计数器 方法区:Java 8以后没有方法区,改为了元空间(MetaSpace) 虚拟机栈 堆 本地方法栈 程序计数器 它可以看作是当前线程所执行的字节码的行号指示器。在Java虚拟机的概念模型里,…...

vue js金额转中文
在Vue.js项目中,实现金额转中文的功能通常涉及编写一个JavaScript方法来处理数字转换逻辑,并在Vue组件中调用该方法。下面是一个基本的示例,展示如何在Vue组件中定义一个计算属性或方法来实现这一功能: /*** 思路: …...
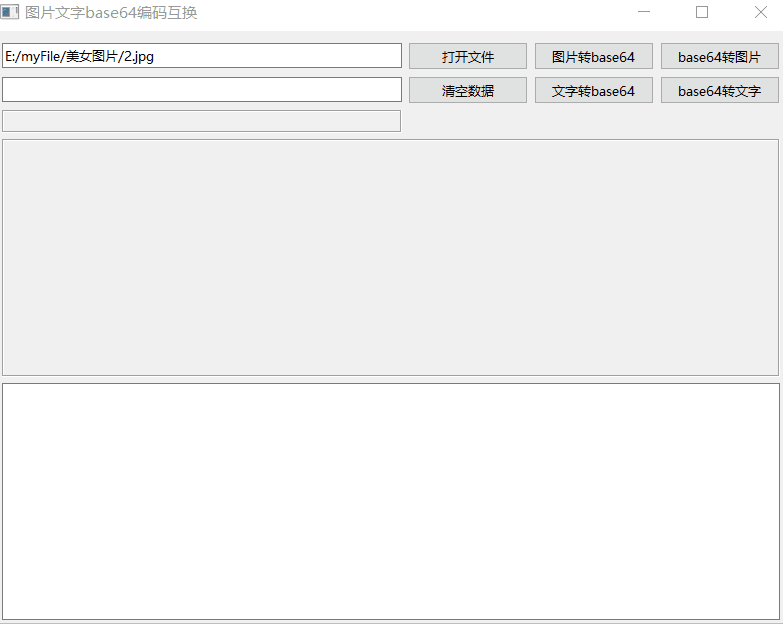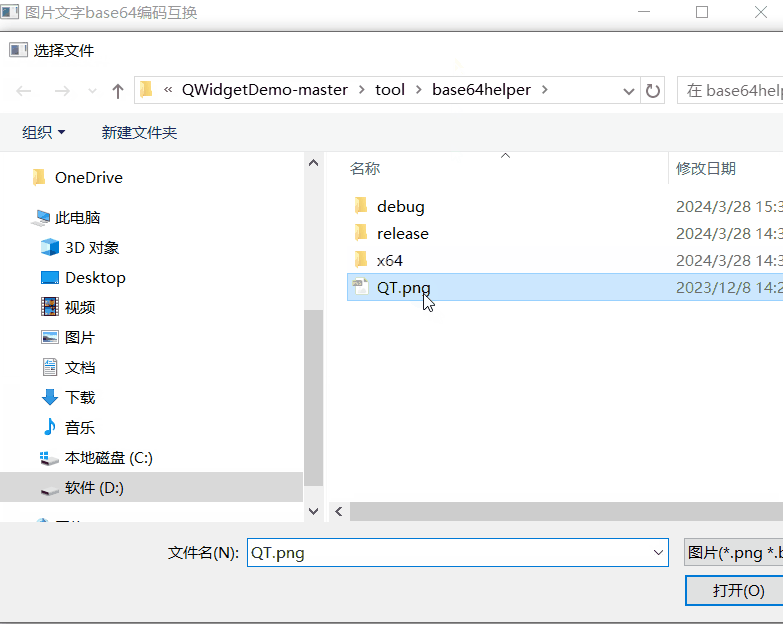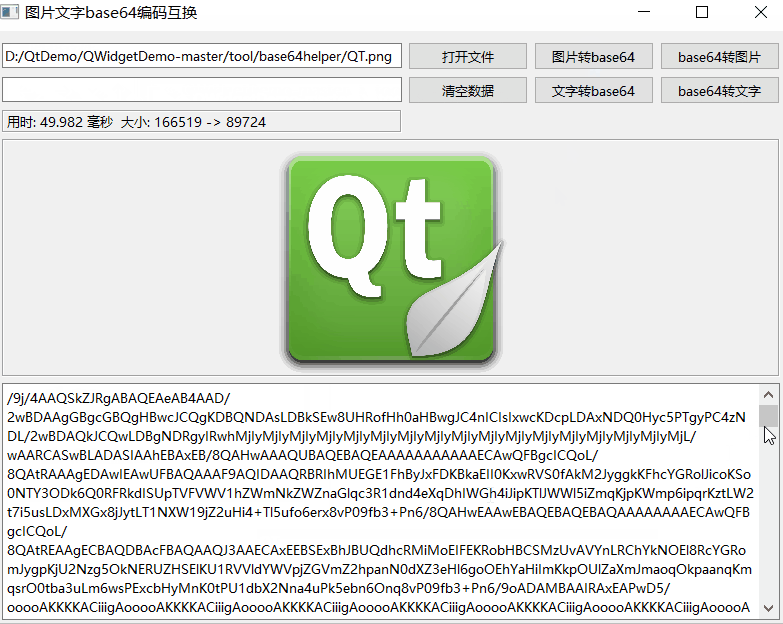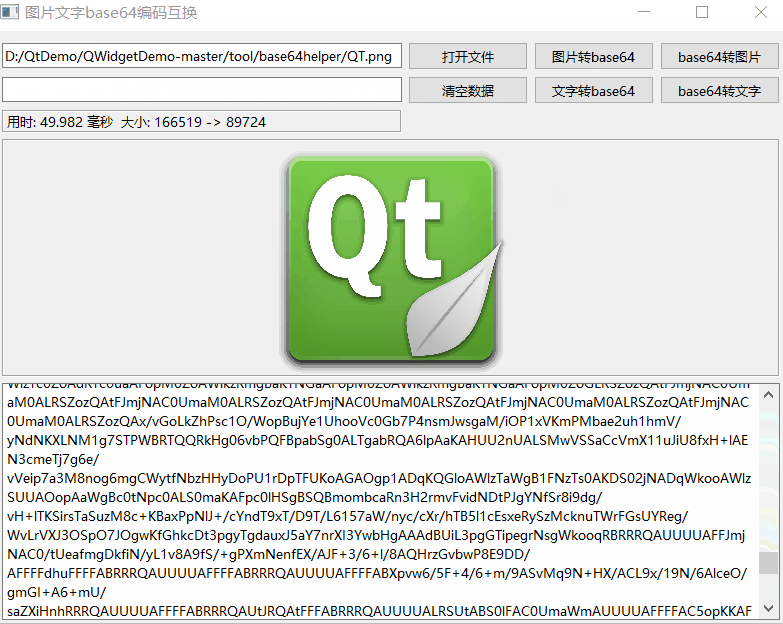
《QT实用小工具·二》图片文字转base64编码
1、概述 源码放在文章末尾 base64编码转换类 图片转base64字符串。base64字符串转图片。字符转base64字符串。base64字符串转字符。后期增加数据压缩。Qt6对base64编码转换进行了重写效率提升至少200%。 下面是demo演示: 项目部分代码如下所示: #ifn…...
Django安装及第一个项目
1、安装python C:\Users\leell>py --version Python 3.10.6 可以看出我的环境python的版本3.10.6,比较新 2、 Python 虚拟环境创建 2.1 官网教程 目前,有两种常用工具可用于创建 Python 虚拟环境: venv 在 Python 3.3 及更高版本中默…...

专升本-物联网
物联网(IOT,Internet of things) 体系结构: 感知层(感知执行层) 网络层 应用层 基本特征: 全面感知 可靠传输 智能处理 作用: 信息采集、转换、收集 信息传递和处理 数据…...

二叉树的遍历C语言
二叉树作为FDS课程最核心的数据结构之一,要求每个人都掌握! 这是一道简单的二叉树问题! 我们将给出一颗二叉树,请你输出它的三种遍历,分别是先序遍历,中序遍历,后序遍历! 输入格式…...
PostgreSQL到Doris的迁移技巧:实时数据同步新选择!
PostgreSQL可以说是目前比较抢手的关系型数据库了,除了兼具多样功能和强大性能之外,还具备非常优秀的可扩展性,更重要的是它还开源,能火不是没有理由的。 虽然PostgreSQL很强大,但是它也有短板,相对于专业…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

yaml读取写入常见错误 (‘cannot represent an object‘, 117)
错误一:yaml.representer.RepresenterError: (‘cannot represent an object’, 117) 出现这个问题一直没找到原因,后面把yaml.safe_dump直接替换成yaml.dump,确实能保存,但出现乱码: 放弃yaml.dump,又切…...
