当前位置： 首页 > news >正文

Linux进程的基本概念

news 2026/1/21 7:19:33
冯诺依曼体系结构
我们常见的计算机，如笔记本。我们不常见的计算机，如服务器，大部分都遵守冯诺依曼体系。
截至目前，我们所认识的计算机，都是有一个个的硬件组件组成
输入单元：包括键盘 , 鼠标，扫描仪 , 写板等
中央处理器 (CPU) ：含有运算器和控制器等
输出单元：显示器，打印机等
关于冯诺依曼，必须强调几点：
这里的存储器指的是内存
不考虑缓存情况，这里的 CPU 能且只能对内存进行读写，不能访问外设 ( 输入或输出设备 )
外设 ( 输入或输出设备 ) 要输入或者输出数据，也只能写入内存或者从内存中读取。
一句话，所有设备都只能直接和内存打交道。
对冯诺依曼的理解，不能停留在概念上，要深入到对软件数据流理解上，请解释，从你登录上 qq 开始和某位朋友聊
天开始，数据的流动过程。 从你打开窗口，开始给他发消息，到他的到消息之后的数据流动过程。如果是在 qq 上发
送文件呢？
操作系统 (Operator System)
概念
任何计算机系统都包含一个基本的程序集合，称为操作系统 (OS) 。笼统的理解，操作系统包括：
内核（进程管理，内存管理，文件管理，驱动管理）
其他程序（例如函数库， shell 程序等等）
设计 OS 的目的
与硬件交互，管理所有的软硬件资源
为用户程序（应用程序）提供一个良好的执行环境
定位
在整个计算机软硬件架构中，操作系统的定位是： 一款纯正的 “ 搞管理 ” 的软件
如何理解 " 管理 "
管理的例子
描述被管理对象
组织被管理对象
总结
计算机管理硬件
1. 描述起来，用 struct 结构体
2. 组织起来，用链表或其他高效的数据结构
系统调用和库函数概念
在开发角度，操作系统对外会表现为一个整体，但是会暴露自己的部分接口，供上层开发使用，这部分
由操作系统提供的接口，叫做系统调用。
系统调用在使用上，功能比较基础，对用户的要求相对也比较高，所以，有心的开发者可以对部分系统
调用进行适度封装，从而形成库，有了库，就很有利于更上层用户或者开发者进行二次开发。
承上启下
那在还没有学习进程之前，就问大家，操作系统是怎么管理进行进程管理的呢？很简单，先把进程描述起来，再把
进程组织起来！
进程
~over~

相关文章：

Linux进程的基本概念

冯诺依曼体系结构 我们常见的计算机，如笔记本。我们不常见的计算机，如服务器，大部分都遵守冯诺依曼体系。 截至目前，我们所认识的计算机，都是有一个个的硬件组件组成 输入单元：包括键盘 , 鼠标&#xf…...

编程日记 2024/4/1 1:40:01

设计模式深度解析：AI如何影响装饰器模式与组合模式的选择与应用

​🌈 个人主页：danci_ 🔥 系列专栏：《设计模式》《MYSQL应用》 💪🏻 制定明确可量化的目标，坚持默默的做事。 AI如何影响装饰器模式与组合模式的选择与应用 在今天这个快速发展的技术时代&#…...

编程日记 2024/4/1 1:33:56

JAVA面试大全之微服务篇

目录 1、Spring Cloud 1.1、什么是微服务？谈谈你对微服务的理解？ 1.2、什么是Spring Cloud？ 1.3、springcloud中的组件有那些？ 1.4、具体说说SpringCloud主要项目...

编程日记 2024/4/1 1:32:55

WiFiSpoof for Mac wifi地址修改工具

WiFiSpoof for Mac，一款专为Mac用户打造的网络隐私守护神器，让您在畅游互联网的同时，轻松保护个人信息安全。 软件下载：WiFiSpoof for Mac下载 在这个信息爆炸的时代，网络安全问题日益凸显。WiFiSpoof通过伪装MAC地址&…...

编程日记 2024/4/1 1:27:50

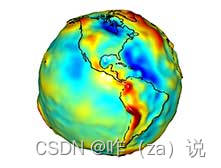
14 - grace数据处理 - 泄露误差改正 - 空域滤波法(Mascon法)

@[TOC](grace数据处理 - 泄露误差改正 - 空域滤波法(Mascon法)) 空域法的基本思想是假设地面某区域的质量变化是由一系列位置已知、质量未知的质量块（小范围区域）引起的，那么将GRACE反演的结果归算到n个质量块上的过程就是泄露信号恢复的过程。个人理解是这样的：假定已知研…...

编程日记 2024/4/1 1:25:48

openGauss MySQL兼容性增强

MySQL兼容性增强 可获得性 本特性自openGauss 3.0.0版本开始引入。 特性简介 本特性主要从以下几方面增强openGauss与MySQL的兼容性（只列举部分典型语法，详情请参见《数据迁移指南》中“MySQL兼容性说明”章节）：。 支持用户锁…...

编程日记 2024/4/1 1:23:46

【跟小嘉学 Linux 系统架构与开发】二、Linux发型版介绍与基础常用命令介绍

系列文章目录 【跟小嘉学 Linux 系统架构与开发】一、学习环境的准备与Linux系统介绍 【跟小嘉学 Linux 系统架构与开发】二、Linux发型版介绍与基础常用命令介绍 文章目录 系列文章目录[TOC](文章目录) 前言一、 Linux 发行版(Linux distribution)介绍二、Centos 虚拟机初始化…...

编程日记 2024/4/1 1:22:44

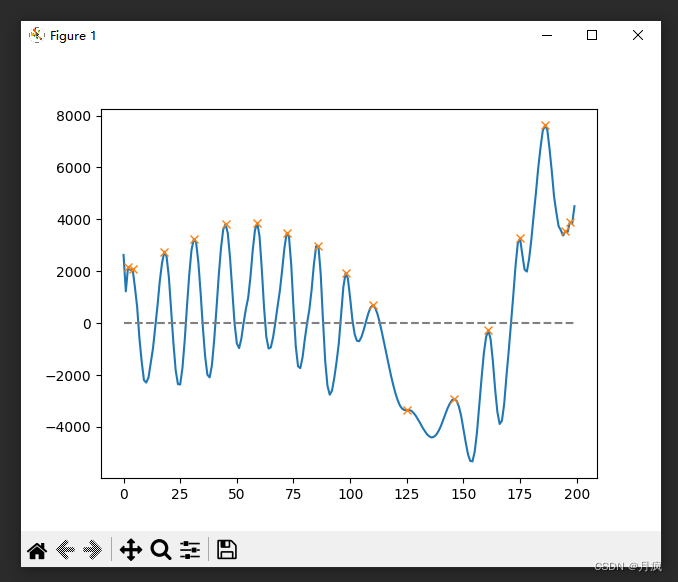
EMD关于信号的重建，心率提取

关于EMD的俩个假设： IMF 有两个假设条件： 在整个数据段内，极值点的个数和过零点的个数必须相等或相差最多不能超过一 个；在任意时刻，由局部极大值点形成的上包络线和由局部极小值点形成的下包络线 的平均值为零&#x…...

编程日记 2024/4/1 1:20:42

HEVC的Profile和Level介绍

文章目录 HEVCProfile（配置）：Level（级别）：划分标准 HEVC HEVC（High Efficiency Video Coding），也称为H.265，是一种视频压缩标准，旨在提供比先前的…...

编程日记 2024/4/1 1:19:41

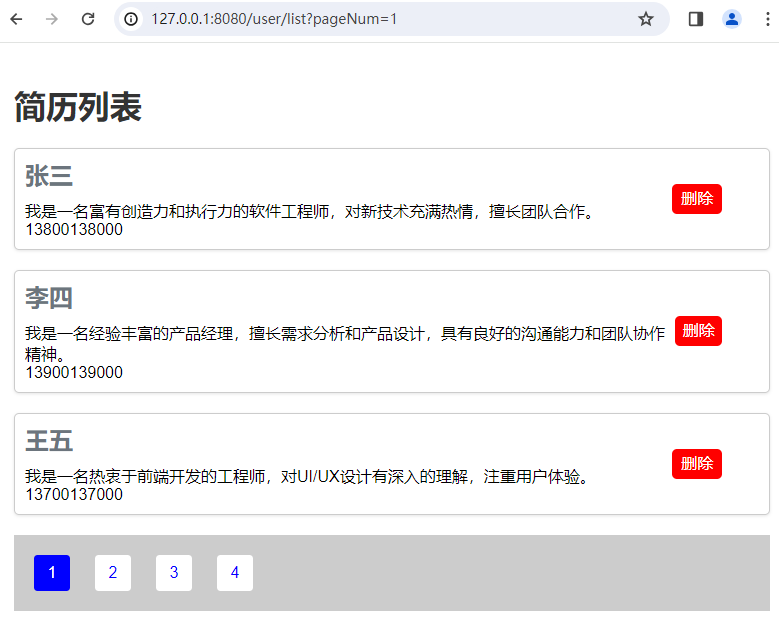
Springboot Thymeleaf 实现数据添加、修改、查询、删除

1、引言 在Spring Boot中使用Thymeleaf模板引擎实现数据的添加、修改、查询和删除功能，通常步骤如下： 在Controller类中，定义处理HTTP请求的方法。创建Thymeleaf模板来处理表单的显示和数据的绑定。 2、用户数据添加 1、 在Controller类中…...

编程日记 2024/4/1 1:17:40

关于 UnityEditorWindow

想要使用UnityEditorWindow作为调试窗口吗？ 这样做可以很方便的针对游戏中的重要对象做调试。 但是有一个很不方便的地方，OnGUI 的刷新频率不高，或者说需要鼠标点击之后才会重绘，如何解决这一问题？ 可以如下操作&am…...

编程日记 2024/4/1 1:16:38

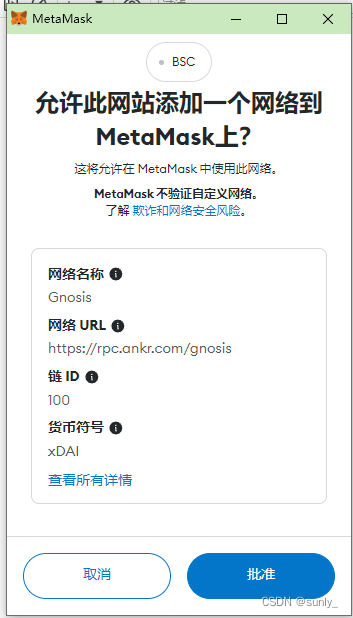
小狐狸JSON-RPC：wallet_addEthereumChain（添加指定链）

wallet_addethereumchain（添加网络） var res await window.ethereum.request({"method": "wallet_addEthereumChain","params": [{"chainId": "0x64", // 链 ID （必填）"…...

编程日记 2024/4/1 1:12:34

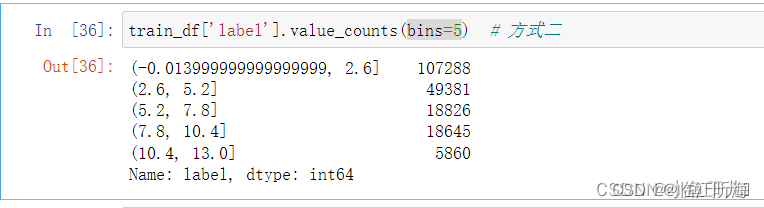
Pandas | value_counts() 的详细用法

value_counts() 函数得作用 用来统计数据表中，指定列里有多少个不同的数据值，并计算每个不同值有在该列中的个数，同时还能根据指定得参数返回排序后结果。 返回得是Series对象 value_counts(values,sortTrue, ascendingFalse, normalizeFal…...

编程日记 2024/4/1 1:04:20

上岸美团了！

Hello，大家好，最近春招正在如火如荼，给大家分享一份美团的面经，作者是一份某双非的硕（只如初见668），刚刚通过了美团的3轮面试，已经拿到offer，以下是他的一些分享。 一面&…...

编程日记 2024/4/1 1:00:15

Gemma开源AI指南

近几个月来，谷歌推出了 Gemini 模型，在人工智能领域掀起了波澜。 现在，谷歌推出了 Gemma，再次引领创新潮流，这是向开源人工智能世界的一次变革性飞跃。 与前代产品不同，Gemma 是一款轻量级、小型模型&…...

编程日记 2024/4/1 0:58:13

LabVIEW智能家居安防系统

LabVIEW智能家居安防系统 随着科技的飞速发展和人们生活水平的不断提升，智能家居系统以其便利性和高效性，逐渐成为现代生活的新趋势。智能家居安防系统作为智能家居系统的重要组成部分，不仅能够提高家庭的安全性，还能为用户提供更…...

编程日记 2024/4/1 0:55:10

[蓝桥杯 2022 省 A] 求和

[蓝桥杯 2022 省 A] 求和 题目描述 给定 n n n 个整数 a 1 , a 2 , ⋯ , a n a_{1}, a_{2}, \cdots, a_{n} a1​,a2​,⋯,an​, 求它们两两相乘再相加的和，即 S a 1 ⋅ a 2 a 1 ⋅ a 3 ⋯ a 1 ⋅ a n a 2 ⋅ a 3 ⋯ a n − 2 ⋅ a n − 1 a n − 2 ⋅ a…...

编程日记 2024/4/1 0:54:09

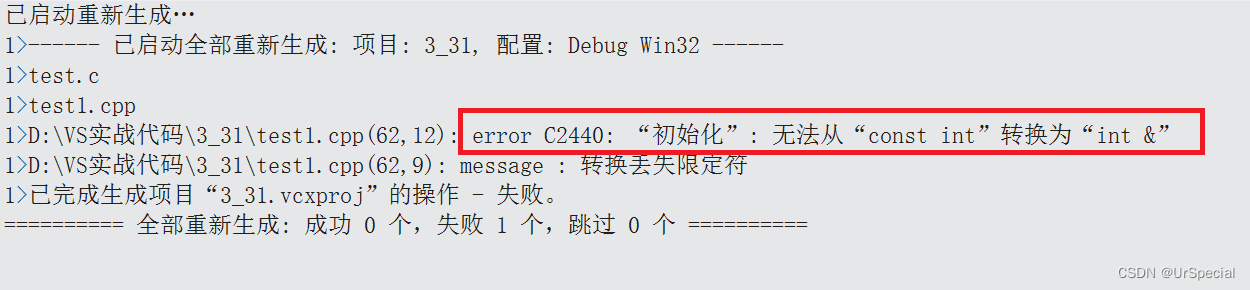
【C++入门】输入输出、命名空间、缺省参数、函数重载、引用、内联函数、auto、基于范围的for循环

目录 命名空间 命名空间的定义 命名空间的使用 输入输出 缺省参数 函数重载 引用 常引用 引用的使用场景 内联函数 auto 基于范围的for循环 命名空间 请看一段C语言的代码&#xff1a; #include <stdio.h> #include <stdlib.h>int rand 10;int main…...

编程日记 2024/4/1 0:53:08

Docker + Nginx 安装

安装Docker 1.防火墙 2.yum源 3.安装基础软件 更新yum源 wget -O /etc/yum.repos.d/CentOS-Base.repo http://mirrors.aliyun.com/repo/Centos-7.repo wget -O /etc/yum.repos.d/epel.repo http://mirrors.aliyun.com/repo/epel-7.repo yum clean all #清除yum源缓存 yu…...

编程日记 2024/4/1 0:51:05

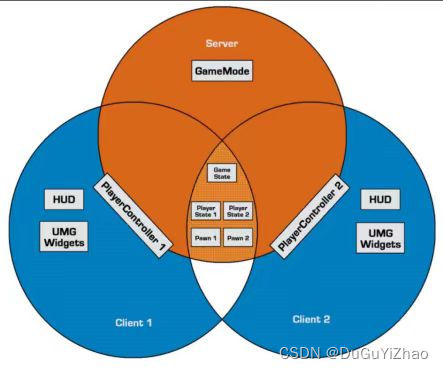
UE RPC 外网联机（1）

技术&#xff1a;RPC TCP通信 设计&#xff1a;大厅服务<---TCP--->房间服务<---RPC--->客户端&#xff08;Creator / Participator&#xff09; 1. PlayerController 用于RPC通信控制 2.GameMode 用于数据同步 3.类图 4. 注意 &#xff08;1&#xff09;RPC&a…...

编程日记 2024/4/1 0:43:58

深度学习在微纳光子学中的应用

深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向&#xff1a; 逆向设计 通过神经网络快速预测微纳结构的光学响应&#xff0c;替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

编程新知 2026/1/20 3:14:06

拉力测试cuda pytorch 把 4070显卡拉满

import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试&#xff0c;通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小&#xff0c;增大可提高计算复杂度duration: 测试持续时间&#xff08;秒&…...

编程新知 2025/12/7 12:35:20

嵌入式常见 CPU 架构

架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集&#xff0c;单周期执行&#xff1b;低功耗、CIP 独立外设&#xff1b;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel&#xff08;原始…...

编程新知 2025/6/10 21:24:01

SQL Server 触发器调用存储过程实现发送 HTTP 请求

文章目录 需求分析解决第 1 步：前置条件，启用 OLE 自动化方式 1：使用 SQL 实现启用 OLE 自动化方式 2：Sql Server 2005启动OLE自动化方式 3：Sql Server 2008启动OLE自动化第 2 步：创建存储过程第 3 步：创建触发器扩展 - 如何调试？第 1 步：登录 SQL Server 2008第 2 步…...

编程新知 2025/9/11 6:56:11

GraphQL 实战篇：Apollo Client 配置与缓存

GraphQL 实战篇&#xff1a;Apollo Client 配置与缓存 上一篇&#xff1a;GraphQL 入门篇&#xff1a;基础查询语法 依旧和上一篇的笔记一样&#xff0c;主实操&#xff0c;没啥过多的细节讲解&#xff0c;代码具体在&#xff1a; https://github.com/GoldenaArcher/graphql…...

编程新知 2026/1/20 9:41:54

针对药品仓库的效期管理问题，如何利用WMS系统“破局”

案例&#xff1a; 某医药分销企业&#xff0c;主要经营各类药品的批发与零售。由于药品的特殊性&#xff0c;效期管理至关重要&#xff0c;但该企业一直面临效期问题的困扰。在未使用WMS系统之前&#xff0c;其药品入库、存储、出库等环节的效期管理主要依赖人工记录与检查。库…...

编程新知 2026/1/19 20:16:25

智警杯备赛--excel模块

数据透视与图表制作 创建步骤 创建 1.在Excel的插入或者数据标签页下找到数据透视表的按钮 2.将数据放进“请选择单元格区域“中&#xff0c;点击确定 这是最终结果&#xff0c;但是由于环境启不了&#xff0c;这里用的是自己的excel&#xff0c;真实的环境中的excel根据实训…...

编程新知 2026/1/20 18:00:54

基于谷歌ADK的 智能产品推荐系统(2): 模块功能详解

在我的上一篇博客&#xff1a;基于谷歌ADK的 智能产品推荐系统(1): 功能简介-CSDN博客 中我们介绍了个性化购物 Agent 项目&#xff0c;该项目展示了一个强大的框架&#xff0c;旨在模拟和实现在线购物环境中的智能导购。它不仅仅是一个简单的聊天机器人&#xff0c;更是一个集…...

编程新知 2026/1/20 15:17:34

RFID推动新能源汽车零部件生产系统管理应用案例

RFID推动新能源汽车零部件生产系统管理应用案例 一、项目背景 新能源汽车零部件场景 在新能源汽车零部件生产领域&#xff0c;电子冷却水泵等关键部件的装配溯源需求日益增长。传统 RFID 溯源方案采用 “网关 RFID 读写头” 模式&#xff0c;存在单点位单独头溯源、网关布线…...

编程新知 2026/1/17 2:59:52

claude3.7高阶玩法，生成系统架构图，国内直接使用

文章目录 零、前言一、操作指南操作指导 二、提示词模板三、实战图书管理系统通过4o模型生成系统描述通过claude3.7生成系统架构图svg代码转换成图片 在线考试系统通过4o模型生成系统描述通过claude3.7生成系统架构图svg代码转换成图片 四、感受 零、前言 现在很多AI大模型可以…...

编程新知 2026/1/15 5:44:56