NEO 学习之 MLE(最大似然估计)
文章目录
- 简单题目
- MLE 在不同的分布的运用
- 正态分布
- 指数分布
- 均匀分布
- 泊松分布
- 如何理解 最大似然估计? 就是我们先取出一堆样本,得到一个L( θ \theta θ) 函数,然后的话,这个是关于 θ \theta θ 的一个函数,那么由于存在即合理,只有概率驱动,也就是这个函数取得最大值的时候,该事件才会发生
简单题目
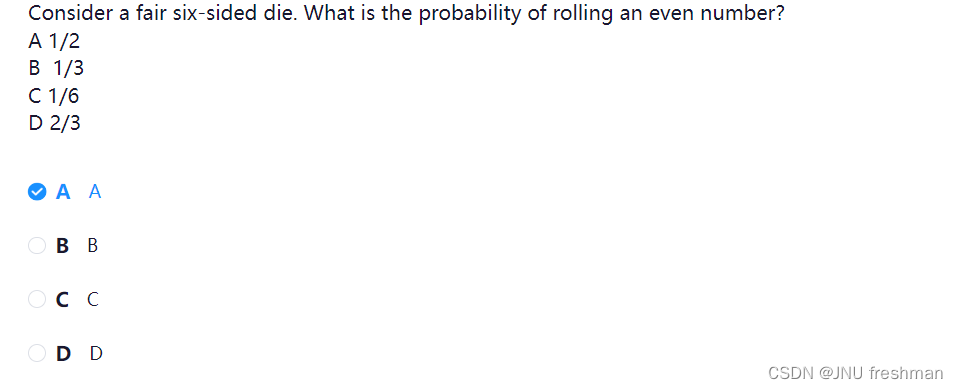
- 此题问的是求丢色子,求得到偶数点的概率
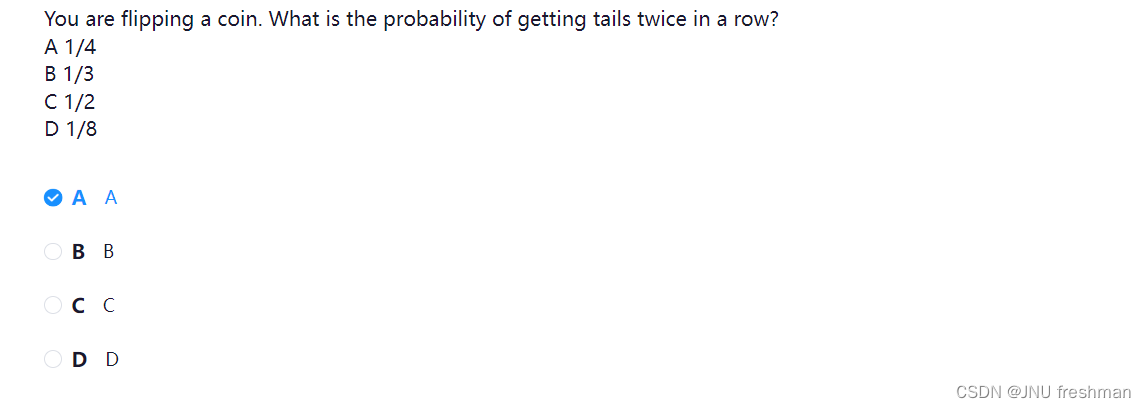
- 求两次都得到硬币的背面的概率

- 拿球问题
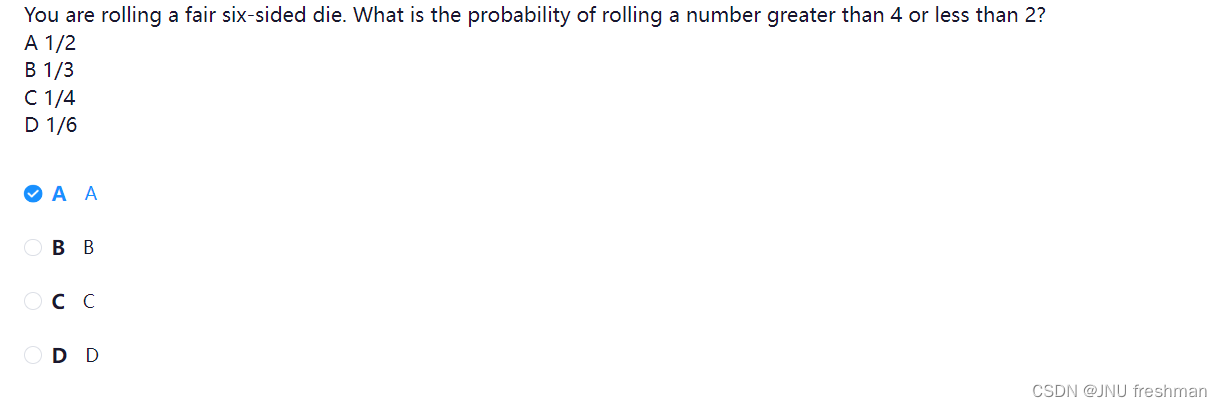
- 符合的点数是 1,5,6
MLE 在不同的分布的运用
正态分布
对于给定的数据集 {1, 3, 4, 6, 7},我们想要估计生成这些数据的正态分布的参数 μ 的最大似然估计(MLE)。
正态分布的概率密度函数(PDF)为:
f ( x ; μ , σ 2 ) = 1 2 π σ 2 exp ( − ( x − μ ) 2 2 σ 2 ) f(x; \mu, \sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(x - \mu)^2}{2\sigma^2}\right) f(x;μ,σ2)=2πσ21exp(−2σ2(x−μ)2)
其中,( μ \mu μ) 表示平均值,( σ 2 \sigma^2 σ2 ) 表示方差。
对于给定的数据集,我们可以使用最大似然估计来找到最适合这些数据的参数( μ \mu μ) 。对于正态分布,( μ \mu μ) 的最大似然估计是数据的平均值。
因此,对于数据集 {1, 3, 4, 6, 7},( μ \mu μ) 的最大似然估计是这些数据的平均值:
μ ^ = 1 + 3 + 4 + 6 + 7 5 = 21 5 = 4.2 \hat{\mu} = \frac{1 + 3 + 4 + 6 + 7}{5} = \frac{21}{5} = 4.2 μ^=51+3+4+6+7=521=4.2
但由于选项中只有整数,我们应选择最接近 4.2 的整数。
最接近 4.2 的整数是 4。
所以,( μ \mu μ) 的最大似然估计是 4。
指数分布
对于给定的数据集 {2, 4, 6, 8, 10},我们想要估计一个指数分布的参数 λ \lambda λ的最大似然估计(MLE)。
指数分布的概率密度函数(PDF)为:
f ( x ; λ ) = λ e − λ x f(x; \lambda) = \lambda e^{-\lambda x} f(x;λ)=λe−λx
对于给定的数据集,我们可以使用最大似然估计来找到最适合这些数据的参数 λ \lambda λ.对于指数分布, λ \lambda λ的最大似然估计是数据的倒数的平均值。
因此,对于数据集 {2, 4, 6, 8, 10}, λ \lambda λ 的最大似然估计为:
λ ^ = n ∑ i = 1 n x i \hat{\lambda} = \frac{n}{\sum_{i=1}^{n} x_i} λ^=∑i=1nxin
其中,( n ) 是数据集的大小,( x i x_i xi ) 是数据集中的第 ( i ) 个数据点。
对于给定的数据集,( n = 5 ),( s u m i = 1 n x i = 2 + 4 + 6 + 8 + 10 = 30 sum_{i=1}^{n} x_i = 2 + 4 + 6 + 8 + 10 = 30 sumi=1nxi=2+4+6+8+10=30)。
因此:
[ λ ^ = 5 30 = 1 6 \hat{\lambda} = \frac{5}{30} = \frac{1}{6} λ^=305=61]
所以, λ \lambda λ 的最大似然估计为 ( 1 6 \frac{1}{6} 61 )。
所以答案是:
B) 1/6
均匀分布
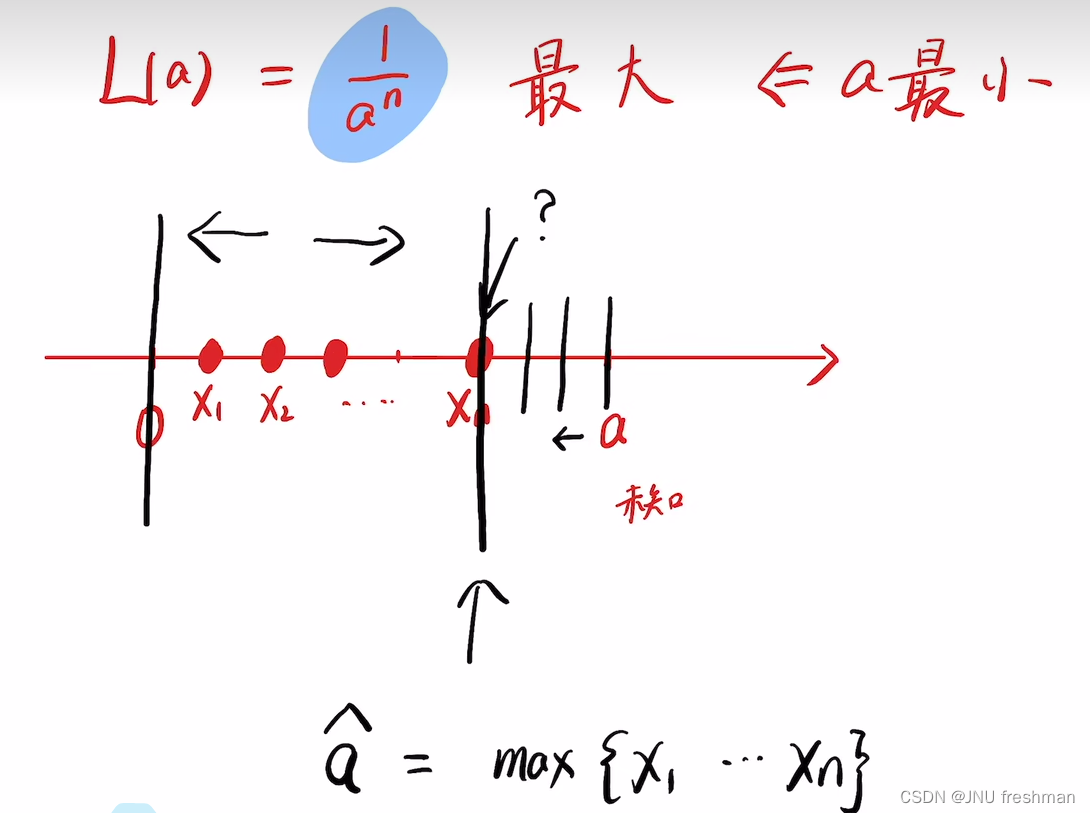
对于给定的数据集 {10, 15, 20, 25, 30},我们想要估计一个在区间 (0, θ) 上的均匀分布的参数 ( θ \theta θ ) 的最大似然估计(MLE)。
在均匀分布中,所有在指定区间内的值都是等可能的。因此,我们可以选择数据集中的最大值作为参数 ( \theta ) 的估计值。
因此,对于数据集 {10, 15, 20, 25, 30},最大值是 30,因此 ( θ \theta θ ) 的最大似然估计是 30。
所以答案是:
D) 30
泊松分布
对于给定的数据集 {3, 5, 7, 9, 11},我们希望估计生成这些数据的泊松分布的参数 μ 的最大似然估计(MLE)。
泊松分布用于描述在固定时间或空间范围内随机事件发生的次数,其概率质量函数为:
P ( X = k ) = e − μ μ k k ! P(X = k) = \frac{e^{-\mu} \mu^k}{k!} P(X=k)=k!e−μμk
其中,( k ) 表示事件发生的次数,( μ \mu μ ) 表示平均发生次数。
对于给定的数据集,泊松分布参数( μ \mu μ ) 的最大似然估计是数据的平均值。
因此,对于数据集 {3, 5, 7, 9, 11},( μ \mu μ ) 的最大似然估计是这些数据的平均值:
[ μ ^ = 3 + 5 + 7 + 9 + 11 5 = 35 5 = 7 \hat{\mu} = \frac{3 + 5 + 7 + 9 + 11}{5} = \frac{35}{5} = 7 μ^=53+5+7+9+11=535=7 ]
所以答案是:
D) 7
相关文章:

NEO 学习之 MLE(最大似然估计)
文章目录 简单题目MLE 在不同的分布的运用正态分布指数分布均匀分布泊松分布 如何理解 最大似然估计? 就是我们先取出一堆样本,得到一个L( θ \theta θ) 函数,然后的话,这个是关于 θ \theta θ 的一个函数,那么由于存…...

going和Java对比有什么不同
语法风格:Golang 和 Java 的语法风格有很大的不同。Golang 更加简单,语法类似于 C 语言,而 Java 比较复杂,语法类似于 C。 并发:Golang 在并发方面有很大的优势,支持轻量级线程 goroutine 和 channel 通信…...

RabbitMQ面经 手打浓缩版
保证可靠性 生产者 本地事务完成和消息发送同时完成 通过事务消息完成 重写confirm在里面做逻辑处理 确保发送成功(不成功就放入到重试队列) MQ 打开持久化确保消息不会丢失 消费者 改成手动回应 不重复消费 生产者 保证不重复发送消息 消费者…...

JavaScript引用数据类型
JS总共分为两种数据类型: 1.基本数据类型 2.引用数据类型 基本数据类型在之前的文章中待大家了解过了 今天我们就来了解一下引用数据类型: 首先呢,我们要知道引用数据类型是存储在哪里的:引用数据类型是存放在堆内存中的对象…...
Mac m1 Flink的HelloWorld
首先在官方下载Downloads | Apache Flink 下载好压缩包后解压,得到Flink文件夹 进入:cd flink-1.19.0 ls 查看里面的文件: 执行启动集群 ./bin/start-cluster.sh 输出显示它已经成功地启动了集群,并且正在启动 standalonesessio…...

3.1 Python变量的定义和使用
Python变量的定义和使用 任何编程语言都需要处理数据,比如数字、字符串、字符等,我们可以直接使用数据,也可以将数据保存到变量中,方便以后使用。 变量(Variable)可以看成一个小箱子,专门用来…...

OceanBase中左外连接和反连接的经验分享
本文作者:张瑞远,曾从事银行、证券数仓设计、开发、优化类工作,现主要从事电信级IT系统及数据库的规划设计、架构设计、运维实施、运维服务、故障处理、性能优化等工作。 持有Orale OCM,MySQL OCP及国产代表数据库认证。 获得的专业技能与认证…...
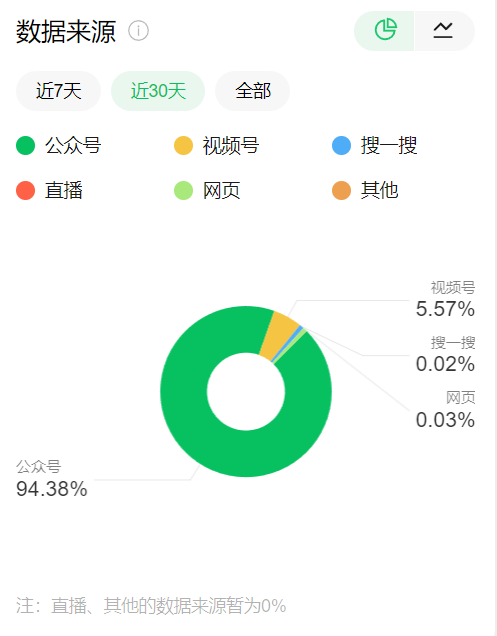
如何提升公众号搜索量?分享内部运营的5步优化技术!
最近一直有自媒体同行朋友在写关于公众号的内容,很多都说公众号现在没得玩了。其实,在运营自媒体上面,思维不通,技术不到位,哪个平台都不适合你玩。 想要在自媒体上面运营变现,一定不要先点击广告变现&…...

【2024】根据系统平均负载情况排查隐患
查看系统负载情况的时候可以使用top和uptime命令。 其中top是一个比较综合的命令,如果我们只需要查看负载情况,可以直接使用uptime命令即可。 uptime命令是一个查看系统运行时间和负载情况的命令,分为四个部分: 系统当前时间系统运行时间当前登录用户数系统平均负载:分别…...
分类任务中的评估指标:Accuracy、Precision、Recall、F1
概念理解 T P TP TP、 T N TN TN、 F P FP FP、 F N FN FN精度/正确率( A c c u r a c y Accuracy Accuracy) 二分类查准率 P r e c i s i o n Precision Precision,查全率 R e c a l l Recall Recall 和 F 1 − s c o r e F1-score F1−s…...

android 音视频基础知识--个人笔记
avi,mkv封装格式数据------》音频流,视频流//字母流(国外会分开) ----〉解封装,解复用打开封装格式 -----》视频压缩数据---压缩H264,H265 -------〉视频解码 ----》原始数据YUV -----〉音频压缩数据---…...
信息工程大学第五届超越杯程序设计竞赛(同步赛)题解
比赛传送门 博客园传送门 c 模板框架 #pragma GCC optimize(3,"Ofast","inline") #include<bits/stdc.h> #define rep(i,a,b) for (int ia;i<b;i) #define per(i,a,b) for (int ia;i>b;--i) #define se second #define fi first #define e…...

Python:文件读写
一、TXT文件读写 Python中用open()函数来读写文本文件,返回文件对象,以下是函数语法。 open(<name>, <mode>, <buffering>,<encoding)name:文件名。 mode:打开文件模式。 buffering:设…...

10.windows ubuntu 组装软件:spades,megahit
Spades 是一种用于组装测序数据的软件,特别适用于处理 Illumina 测序平台产生的数据。它的全称是 "St. Petersburg genome assembler",是一款广泛使用的基因组组装工具。 第一种:wget https://cab.spbu.ru/files/release3.15.3/S…...

K8S之Secret的介绍和使用
Secret Secret的介绍Secret的使用通过环境变量引入Secret通过volume挂载Secret Secret的介绍 Secret是一种保护敏感数据的资源对象。例如:密码、token、秘钥等,而不需要把这些敏感数据暴露到镜像或者Pod Spec中。Secret可以以Volume或者环境变量的方式使…...
git下载安装教程
git下载地址 有一个镜像的网站可以提供下载: https://registry.npmmirror.com/binary.html?pathgit-for-windows/图太多不截了哈哈,一直next即可。...
《剑指 Offer》专项突破版 - 面试题 98、99 和 100 : 和动态规划相关的矩阵路径问题(C++ 实现)
目录 前言 面试题 98 : 路径的数目 面试题 99 : 最小路径之和 面试题 100 : 三角形中最小路径之和 前言 矩阵路径是一类常见的可以用动态规划来解决的问题。这类问题通常输入的是一个二维的格子,一个机器人按照一定的规则从格子的某个位置走到另一个位置&#…...
)
KY145 EXCEL排序(用Java实现)
描述 Excel可以对一组纪录按任意指定列排序。现请你编写程序实现类似功能。 对每个测试用例,首先输出1行“Case i:”,其中 i 是测试用例的编号(从1开始)。随后在 N 行中输出按要求排序后的结果,即:当 C…...

属性选择器
1.[title]{background:yellow;}:所有带title标签设置成黄色 2.div[class]{background:yellow;}:所有div中带class标签设置成黄色 3.div[classbox1]{border:1px solid blue; }:div中包含class并且classbox1的设置成蓝边框 4. class…...

软考 - 系统架构设计师 - 关系模型的完整性规则
前言 关系模型的完整性规则是一组用于确保关系数据库中数据的完整性和一致性的规则。这些规则定义了在关系数据库中如何存储、更新和查询数据,以保证数据的准确性和一致性。 详情 关系模型的完整性规则主要包括以下三类: 实体完整性规则 这是确保每个…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

归并排序:分治思想的高效排序
目录 基本原理 流程图解 实现方法 递归实现 非递归实现 演示过程 时间复杂度 基本原理 归并排序(Merge Sort)是一种基于分治思想的排序算法,由约翰冯诺伊曼在1945年提出。其核心思想包括: 分割(Divide):将待排序数组递归地分成两个子…...
