分类任务中的评估指标:Accuracy、Precision、Recall、F1
- 概念理解
- 二分类
- 三分类
概念理解
T P TP TP、 T N TN TN、 F P FP FP、 F N FN FN
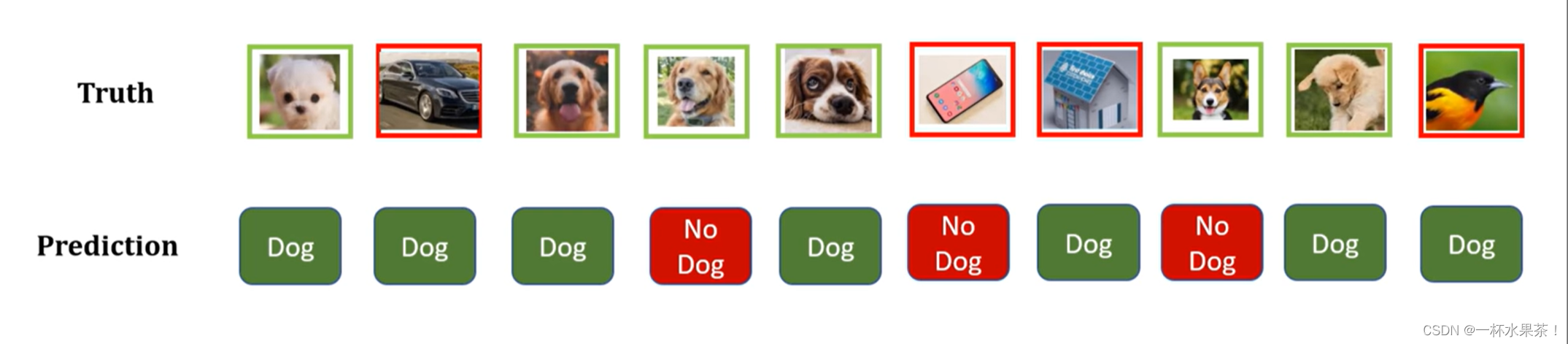
在这个二分类模型中,只有 是「狗」 或 不是「狗」。

只看模型的预测为「狗」即 P r e d i c t i o n = D o g Prediction=Dog Prediction=Dog,共有 7 个如绿色方格所示。其中,
- 真实为「狗」且被模型正确预测为「狗」的有 4 个,这就是 T r u e P o s i t i v e = 4 True\ Positive=4 True Positive=4( T P TP TP);
- 真实不为「狗」但被模型错误预测为「狗」的有 3 个,这就是 F a l s e P o s i t i v e = 3 False\ Positive=3 False Positive=3( F P FP FP)。

只看模型的预测不为「狗」即 P r e d i c t i o n = N o D o g Prediction=No\ Dog Prediction=No Dog,共有 3 个如红色方格所示。其中,
- 真实不为「狗」且被模型正确预测不为「狗」的有 1 个,这就是 T r u e N e g a t i v e = 1 True\ Negative=1 True Negative=1( T N TN TN);
- 真实为「狗」但被模型错误预测不为「狗」的有 2 个,这就是 F a l s e N e g a t i v e = 2 False\ Negative=2 False Negative=2( F N FN FN)。
精度/正确率( A c c u r a c y Accuracy Accuracy)
- 误差( E r r o r Error Error):学习器的 预测输出 与样本的 真实输出 之间的差异。
- 错误率:错误分类的样本 占据 总样本 的比例。
精度( A c c u r a c y Accuracy Accuracy)= 1- 错误率,即 正确分类的样本占总样本的比例。

A c c u r a c y Accuracy Accuracy 是分类问题中最常用的指标。但是,对于不平衡数据集而言, A c c u r a c y Accuracy Accuracy 并不是一个好指标。 W h y ? Why? Why?
假设有 100 张图片,其中 98 张图片是「狗」,1 张是「猫」,1 张是「猪」,要训练一个三分类器,能正确识别图片里动物的类别。
- 其中,狗这个类别就是大多数类( M a j o r i t y C l a s s Majority\ Class Majority Class)。
- 当大多数类中样本(狗)的数量远超过其他类别(猫、猪)时,如果采用 A c c u r a c y Accuracy Accuracy 来评估分类器的好坏,那么即便模型性能很差(如无论输入什么图片,都预测为「狗」),也可以得到较高的 A c c u r a c y S c o r e Accuracy\ Score Accuracy Score(如 98%)。
- 此时,虽然 A c c u r a c y S c o r e Accuracy\ Score Accuracy Score 很高,但是意义不大。
- 当数据异常不平衡时, A c c u r a c y Accuracy Accuracy 评估方法的缺陷尤为显著。
因此,需要引入 P r e c i s i o n Precision Precision (精准度), R e c a l l Recall Recall (召回率)和 F 1 − s c o r e F1-score F1−score 评估指标。
考虑到二分类和多分类模型中,评估指标的计算方法略有不同,下面分开讨论。
二分类
在二分类问题中,假设该样本一共有两种类别: P o s i t i v e Positive Positive 和 N e g a t i v e Negative Negative。
当分类器预测结束,可以绘制出混淆矩阵( C o n f u s i o n M a t r i x Confusion\ Matrix Confusion Matrix),如下图,
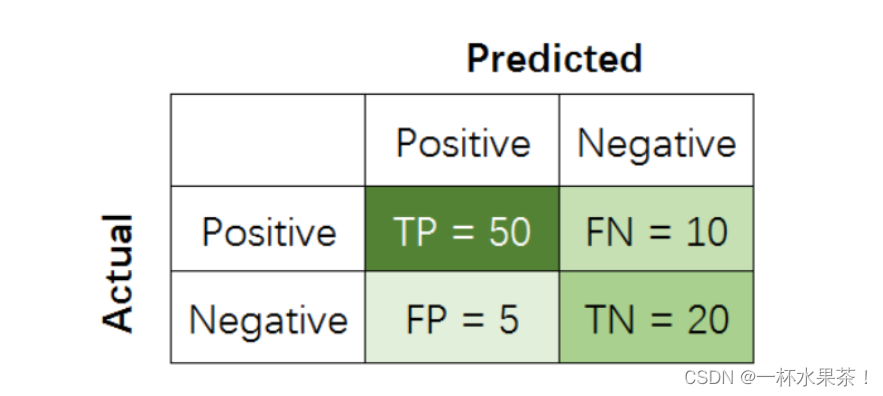
其中分类结果分为如下几种:
- T r u e P o s i t i v e True\ Positive True Positive( T P TP TP):把正样本成功预测为正。
- T r u e N e g a t i v e True\ Negative True Negative( T N TN TN):把负样本成功预测为负。
- F a l s e P o s i t i v e False\ Positive False Positive( F P FP FP):把负样本错误预测为正。
- F a l s e N e g a t i v e False\ Negative False Negative( F N FN FN):把正样本错误预测为负。
有了混淆矩阵的 T P TP TP、 T N TN TN、 F P FP FP 和 F N FN FN,下面计算 P r e c i s i o n Precision Precision、 R e c a l l Recall Recall 和 F 1 − s c o r e F1-score F1−score。
查准率 P r e c i s i o n Precision Precision,查全率 R e c a l l Recall Recall 和 F 1 − s c o r e F1-score F1−score 的计算
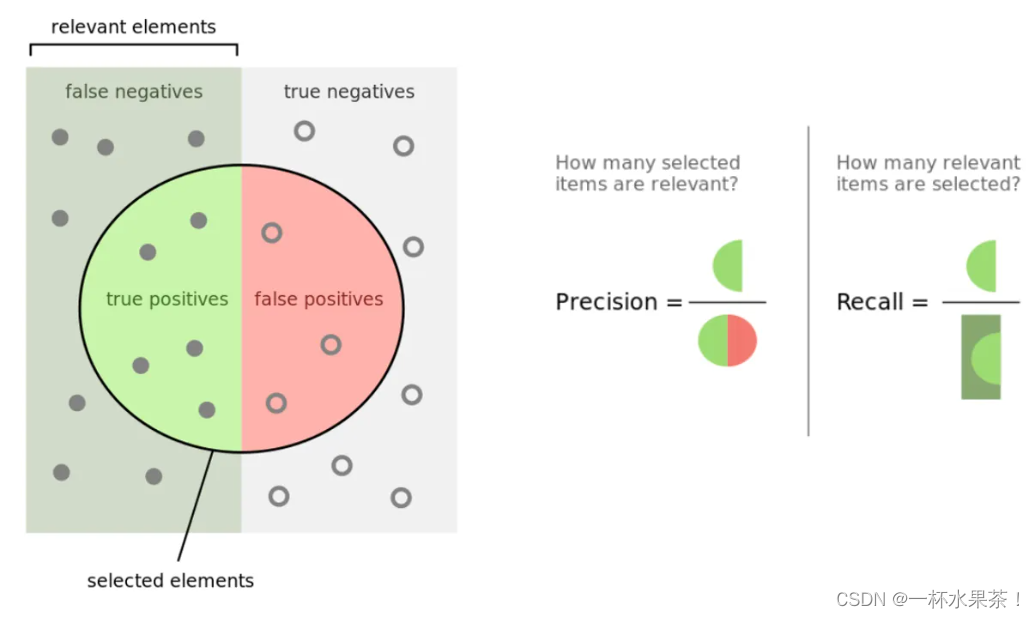
- 准确率:关注预测的准确性,在 所有被预测为 P o s i t i v e Positive Positive 的样本 中,有多少是正确的(有多少 T r u e True True 的 P o s i t i v e Positive Positive)?
- 召回率:关注预测的全面性,在 所有实际为 P o s i t i v e Positive Positive 的样本 中,有多少被正确预测了(有多少 P o s i t i v e Positive Positive 被揪出来了)?
在二分类模型中, A c c u r a c y Accuracy Accuracy,查准率 P r e c i s i o n Precision Precision,查全率 R e c a l l Recall Recall 和 F 1 − s c o r e F1-score F1−score 的定义如下:
A c c u r a c y = T P + T N T P + T N + F P + F N Accuracy = \frac{TP+TN}{TP+TN+FP+FN} Accuracy=TP+TN+FP+FNTP+TN
P r e c i s i o n = T P T P + F P Precision = \frac{TP}{TP+FP} Precision=TP+FPTP
R e c a l l = T P T P + F N Recall = \frac{TP}{TP+FN} Recall=TP+FNTP
F 1 − s c o r e = 2 × P r e c i s i o n × R e c a l l P r e c i s i o n + R e c a l l F1-score = \frac{2×Precision×Recall}{Precision+Recall} F1−score=Precision+Recall2×Precision×Recall
代入 T P TP TP、 T N TN TN、 F P FP FP 和 F N FN FN 的数值计算即可,如下:
A c c u r a c y = 50 + 20 50 + 20 + 5 + 10 = 14 / 17 Accuracy = \frac{50+20}{50+20+5+10} =14/17 Accuracy=50+20+5+1050+20=14/17
P r e c i s i o n = 50 50 + 5 = 10 / 11 Precision=\frac{50}{50+5}=10/11 Precision=50+550=10/11
R e c a l l = 50 50 + 10 = 5 / 6 Recall=\frac{50}{50+10}=5/6 Recall=50+1050=5/6
F 1 − s c o r e = 2 × 10 11 × 5 6 10 11 + 5 6 = 20 / 23 F1-score=\frac{2×\frac{10}{11}×\frac{5}{6}}{\frac{10}{11}+\frac{5}{6}}=20/23 F1−score=1110+652×1110×65=20/23
查准率 P r e c i s i o n Precision Precision,查全率 R e c a l l Recall Recall 和 F 1 − s c o r e F1-score F1−score 的理解
- P r e c i s i o n Precision Precision 着重评估:在 预测为 P o s i t i v e Positive Positive 的所有数据( T P + F P TP+FP TP+FP)中,真实 P o s i t i v e Positive Positive 的数据( T P TP TP)到底占多少?
- R e c a l l Recall Recall 着重评估:在 所有真实为 P o s i t i v e Positive Positive 数据 ( T P + F N TP+FN TP+FN)中,被 成功预测为 P o s i t i v e Positive Positive 的数据 ( T P TP TP)到底占多少?
举个例子,一个医院新开发了一套癌症 A I AI AI 诊断系统,想评估其性能好坏。把病人得了癌症定义为 P o s i t i v e Positive Positive,没得癌症定义为 N e g a t i v e Negative Negative。那么,到底该用什么指标进行评估呢?
- 如用 P r e c i s i o n Precision Precision 对系统进行评估,那么其回答的问题就是:在诊断为癌症的一堆人中,到底有多少人真得了癌症?
- 如用 R e c a l l Recall Recall 对系统进行评估,那么其回答的问题就是:在一堆得了癌症的病人中,到底有多少人能被成功检测出癌症?
- 如用 A c c u r a c y Accuracy Accuracy 对系统进行评估,那么其回答的问题就是:在一堆癌症病人和正常人中,有多少人被系统给出了正确诊断结果?
O K OK OK,那啥时候应该更注重 R e c a l l Recall Recall 而不是 P r e c i s i o n Precision Precision 呢?
R e c a l l = T P T P + F N Recall = \frac{TP}{TP+FN} Recall=TP+FNTP
当 F a l s e N e g a t i v e False Negative FalseNegative ( F N FN FN)的成本代价很高(后果很严重),希望尽量避免产生 F N FN FN 时,应该着重考虑提高 R e c a l l Recall Recall 指标( F N FN FN 越小, R e c a l l Recall Recall 越高)。
在上述例子里, F a l s e N e g a t i v e False Negative FalseNegative 是得了癌症的病人没有被诊断出癌症,这种情况是最应该避免的。
- 宁可把健康人误诊为癌症 ( F P FP FP),也不能让真正患病的人检测不出癌症 ( F N FN FN) 而耽误治疗离世。
在这里,癌症诊断系统 的目标是:尽可能提高 R e c a l l Recall Recall 值,哪怕牺牲一部分 P r e c i s i o n Precision Precision。
O h o Oho Oho,那啥时候应该更注重 P r e c i s i o n Precision Precision 而不是 R e c a l l Recall Recall 呢?
P r e c i s i o n = T P T P + F P Precision = \frac{TP}{TP+FP} Precision=TP+FPTP
当 F a l s e P o s i t i v e False Positive FalsePositive ( F P FP FP)的成本代价很高(后果很严重)时,即期望尽量避免产生 F P FP FP 时,应该着重考虑提高 P r e c i s i o n Precision Precision 指标( F P FP FP 越小, P r e c i s i o n Precision Precision 越高)。
以垃圾邮件屏蔽系统为例,垃圾邮件为 P o s i t i v e Positive Positive,正常邮件为 N e g a t i v e Negative Negative, F a l s e P o s i t i v e False Positive FalsePositive 是把正常邮件识别为垃圾邮件,这种情况是最应该避免的。
- 宁可把垃圾邮件标记为正常邮件( F N FN FN),也不能让正常邮件直接进垃圾箱( F P FP FP)。>
垃圾邮件屏蔽系统 的目标是:尽可能提高 P r e c i s i o n Precision Precision 值,哪怕牺牲一部分 R e c a l l Recall Recall。
而 F 1 − s c o r e F1-score F1−score 是 P r e c i s i o n Precision Precision 和 R e c a l l Recall Recall 两者的综合。
F 1 − s c o r e = 2 × P r e c i s i o n × R e c a l l P r e c i s i o n + R e c a l l F1-score = \frac{2×Precision×Recall}{Precision+Recall} F1−score=Precision+Recall2×Precision×Recall
假设检察机关想要将罪犯逮捕归案,就需要对所有人群进行分析,判断某人是犯了罪( P o s i t i v e Positive Positive)还是没有犯罪( N e g a t i v e Negative Negative)。
显然,检察机关希望既不错过任何一个罪犯(提高 R e c a l l Recall Recall),也不错判一个无辜者(提高 P r e c i s i o n Precision Precision),因此需要同时考虑 R e c a l l Recall Recall 和 P r e c i s i o n Precision Precision 这两个指标。
- “天网恢恢,疏而不漏,任何罪犯都难逃法网” 更倾向于 R e c a l l Recall Recall。
- “宁可放过一些罪犯,也不冤枉一个无辜者” 更倾向于 P r e c i s i o n Precision Precision。
到底哪种更好呢?显然, P r e c i s i o n Precision Precision 和 R e c a l l Recall Recall 都应该尽可能高,也就是说 F 1 − s c o r e F1-score F1−score 应该尽可能高。
三分类
从特殊
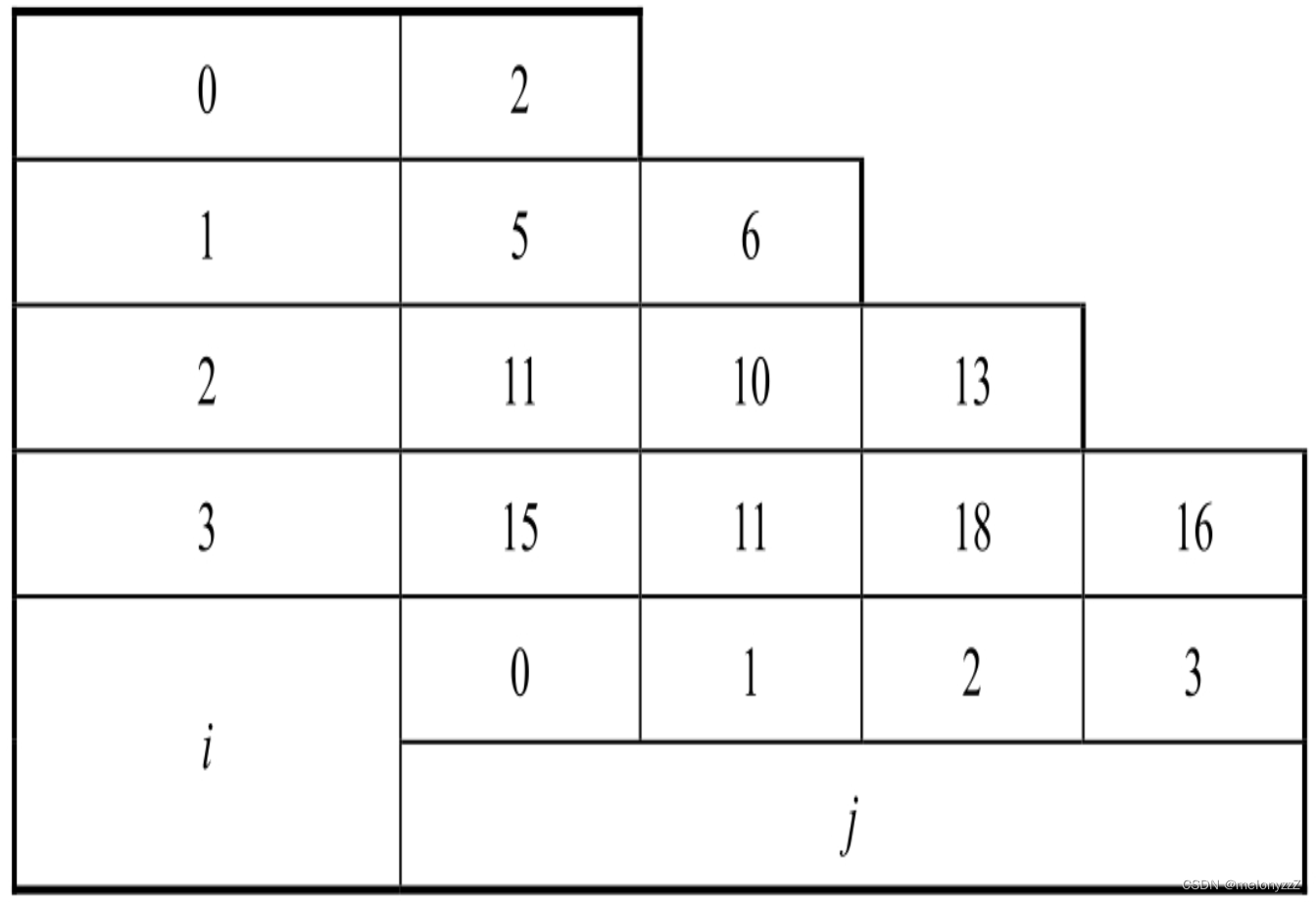
要开发一个动物识别系统,来区分输入图片是猫,狗还是猪。给定分类器一堆动物图片,产生了如下结果混淆矩阵。
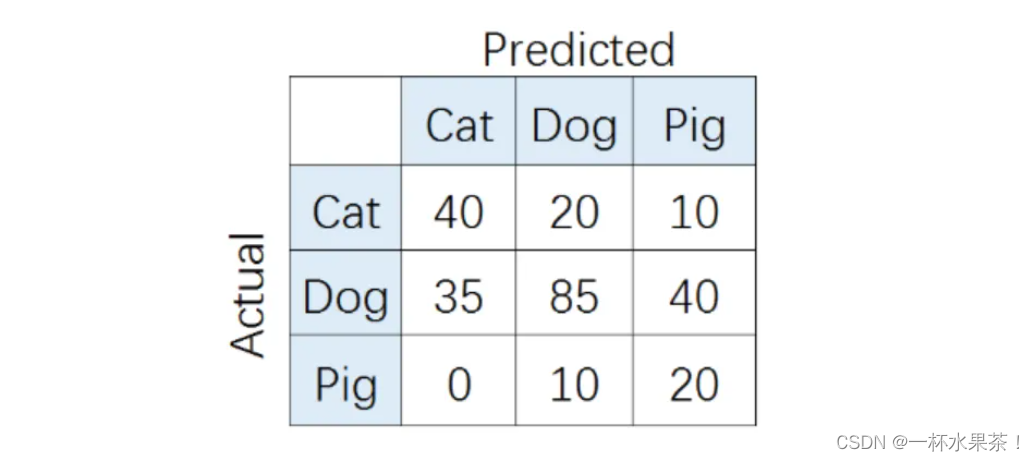
在混淆矩阵中,正确的分类样本( A c t u a l l a b e l = P r e d i c t e d l a b e l Actual\ label = Predicted\ label Actual label=Predicted label)分布在 左上到右下的对角线上。
其中, A c c u r a c y Accuracy Accuracy 的定义为分类正确(对角线上)的样本数与总样本数的比值。
- A c c u r a c y Accuracy Accuracy 度量的是全局样本预测情况。
- 而对于 P r e c i s i o n Precision Precision 和 R e c a l l Recall Recall 而言,每个类都需要单独计算其 P r e c i s i o n Precision Precision 和 R e c a l l Recall Recall。
比如,对类别「猪」而言,其 P r e c i s i o n Precision Precision 和 R e c a l l Recall Recall 分别为:
P r e c i s i o n = T P T P + F P = 20 20 + ( 10 + 40 ) = 2 / 7 Precision = \frac{TP}{TP+FP} = \frac{20}{20+(10+40)} = 2/7 Precision=TP+FPTP=20+(10+40)20=2/7
R e c a l l = T P T P + F N = 20 20 + ( 0 + 10 ) = 2 / 3 Recall = \frac{TP}{TP+FN} = \frac{20}{20+(0+10)} = 2/3 Recall=TP+FNTP=20+(0+10)20=2/3
总的来说,
P r e s i c i o n Presicion Presicion 如下: P c a t = 8 / 15 , P d o g = 1 / 23 , P p i g = 2 / 7 P_{cat}=8/15, P_{dog}=1/23, P_{pig}=2/7 Pcat=8/15,Pdog=1/23,Ppig=2/7
R e c a l l Recall Recall 如下: R c a t = 4 / 7 , R d o g = 17 / 23 , R p i g = 2 / 3 R_{cat}=4/7, R_{dog}=17/23, R_{pig}=2/3 Rcat=4/7,Rdog=17/23,Rpig=2/3
到一般
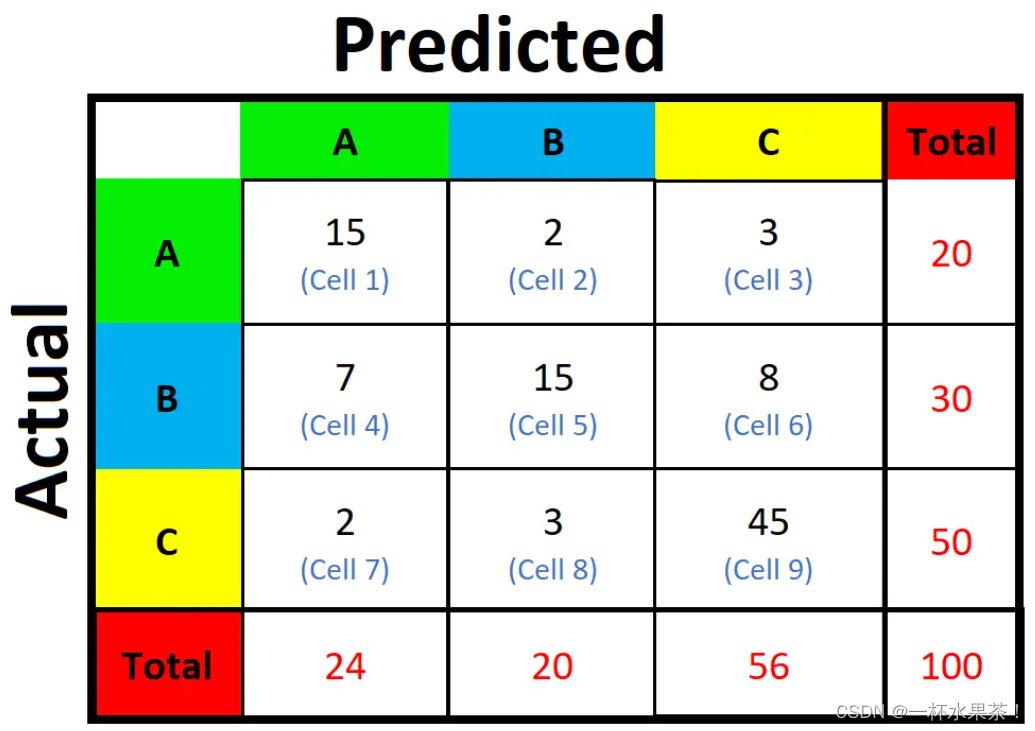
A c c u r a c y Accuracy Accuracy
- A c c u r a c y Accuracy Accuracy :正确分类的样本数 / / / 所有样本数。
(即:左上角到右下角的对角线上的样本数之和 / / / 总样本数 = ( A , A ) + ( B , B ) + ( C , C ) T o t a l \frac{(A,A)+(B,B)+(C,C)}{Total} Total(A,A)+(B,B)+(C,C))。
A c c u r a c y = ( 15 + 15 + 45 ) / 100 = 0.75 Accuracy= (15 +15+ 45)/100 = 0.75 Accuracy=(15+15+45)/100=0.75
P r e c i s i o n Precision Precision
对 A A A 类来说,
- P r e c i s i o n Precision Precision:(预测为正确 & 真实为正确)的样本 / / / 预测为正确的所有样本。
(即: ( A , A ) (A,A) (A,A) 的值 / / / A A A 所在列的 T o t a l A − c o l u m n Total_{A-column} TotalA−column = ( A , A ) ( A , A ) + ( B , A ) + ( C , A ) \frac{(A,A)}{(A,A)+(B,A)+(C,A)} (A,A)+(B,A)+(C,A)(A,A))
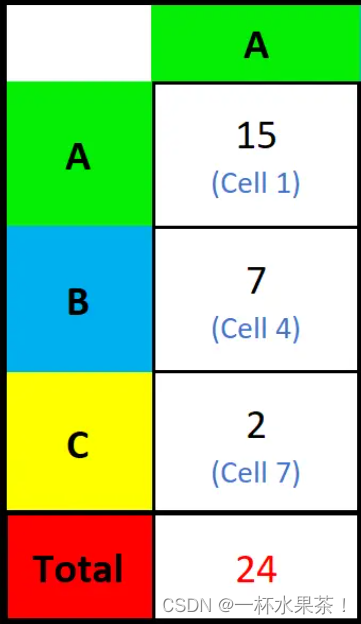
P r e c i s i o n ( A ) = 15 / 24 = 0.625 Precision (A) = 15/24 = 0.625 Precision(A)=15/24=0.625
R e c a l l Recall Recall
- R e c a l l Recall Recall:(预测为正确 & 真实是正确)的样本 / / / 真实是正确的所有样本。
(即: ( A , A ) (A,A) (A,A) 的值 / / / A A A 所在行的 T o t a l A − l i n e Total_{A-line} TotalA−line = ( A , A ) ( A , A ) + ( A , B ) + ( A , C ) \frac{(A,A)}{(A,A)+(A,B)+(A,C)} (A,A)+(A,B)+(A,C)(A,A))
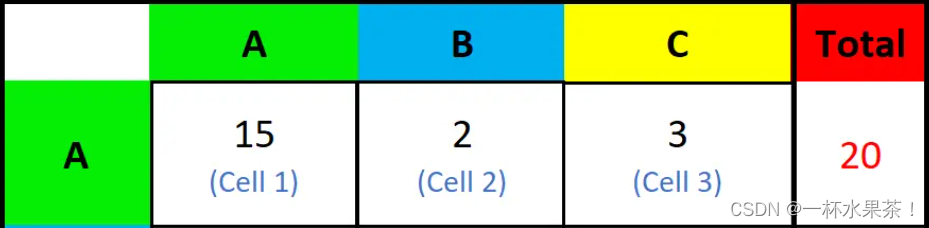
R e c a l l ( A ) = 15 / 20 = 0.75 Recall (A)= 15/20 = 0.75 Recall(A)=15/20=0.75
相关文章:

分类任务中的评估指标:Accuracy、Precision、Recall、F1
概念理解 T P TP TP、 T N TN TN、 F P FP FP、 F N FN FN精度/正确率( A c c u r a c y Accuracy Accuracy) 二分类查准率 P r e c i s i o n Precision Precision,查全率 R e c a l l Recall Recall 和 F 1 − s c o r e F1-score F1−s…...

android 音视频基础知识--个人笔记
avi,mkv封装格式数据------》音频流,视频流//字母流(国外会分开) ----〉解封装,解复用打开封装格式 -----》视频压缩数据---压缩H264,H265 -------〉视频解码 ----》原始数据YUV -----〉音频压缩数据---…...
信息工程大学第五届超越杯程序设计竞赛(同步赛)题解
比赛传送门 博客园传送门 c 模板框架 #pragma GCC optimize(3,"Ofast","inline") #include<bits/stdc.h> #define rep(i,a,b) for (int ia;i<b;i) #define per(i,a,b) for (int ia;i>b;--i) #define se second #define fi first #define e…...

Python:文件读写
一、TXT文件读写 Python中用open()函数来读写文本文件,返回文件对象,以下是函数语法。 open(<name>, <mode>, <buffering>,<encoding)name:文件名。 mode:打开文件模式。 buffering:设…...

10.windows ubuntu 组装软件:spades,megahit
Spades 是一种用于组装测序数据的软件,特别适用于处理 Illumina 测序平台产生的数据。它的全称是 "St. Petersburg genome assembler",是一款广泛使用的基因组组装工具。 第一种:wget https://cab.spbu.ru/files/release3.15.3/S…...

K8S之Secret的介绍和使用
Secret Secret的介绍Secret的使用通过环境变量引入Secret通过volume挂载Secret Secret的介绍 Secret是一种保护敏感数据的资源对象。例如:密码、token、秘钥等,而不需要把这些敏感数据暴露到镜像或者Pod Spec中。Secret可以以Volume或者环境变量的方式使…...
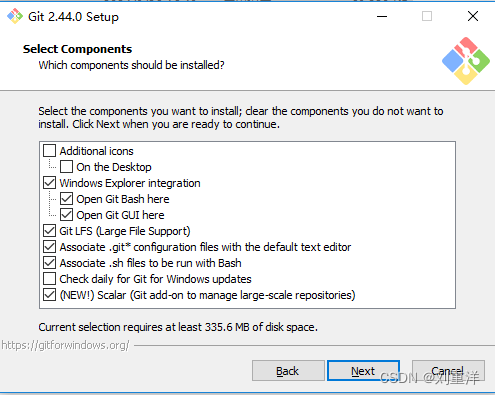
git下载安装教程
git下载地址 有一个镜像的网站可以提供下载: https://registry.npmmirror.com/binary.html?pathgit-for-windows/图太多不截了哈哈,一直next即可。...
《剑指 Offer》专项突破版 - 面试题 98、99 和 100 : 和动态规划相关的矩阵路径问题(C++ 实现)
目录 前言 面试题 98 : 路径的数目 面试题 99 : 最小路径之和 面试题 100 : 三角形中最小路径之和 前言 矩阵路径是一类常见的可以用动态规划来解决的问题。这类问题通常输入的是一个二维的格子,一个机器人按照一定的规则从格子的某个位置走到另一个位置&#…...
)
KY145 EXCEL排序(用Java实现)
描述 Excel可以对一组纪录按任意指定列排序。现请你编写程序实现类似功能。 对每个测试用例,首先输出1行“Case i:”,其中 i 是测试用例的编号(从1开始)。随后在 N 行中输出按要求排序后的结果,即:当 C…...

属性选择器
1.[title]{background:yellow;}:所有带title标签设置成黄色 2.div[class]{background:yellow;}:所有div中带class标签设置成黄色 3.div[classbox1]{border:1px solid blue; }:div中包含class并且classbox1的设置成蓝边框 4. class…...

软考 - 系统架构设计师 - 关系模型的完整性规则
前言 关系模型的完整性规则是一组用于确保关系数据库中数据的完整性和一致性的规则。这些规则定义了在关系数据库中如何存储、更新和查询数据,以保证数据的准确性和一致性。 详情 关系模型的完整性规则主要包括以下三类: 实体完整性规则 这是确保每个…...

写了几个难一点的sql
写了几个难一点的sql SELECT bn.id AS book_node_id, t.version_id, bn.textbook_id, s.id AS subject_id, s.stage_id, COUNT( CASE WHEN d.document_type_id 1 AND d.scope IS NULL AND p.document_id IS NOT NULL THEN 1 END ) AS type_1_count, COUNT( CASEWHEN d.docume…...
【JDK常用的API】包装类
🍬 博主介绍👨🎓 博主介绍:大家好,我是 hacker-routing ,很高兴认识大家~ ✨主攻领域:【渗透领域】【应急响应】 【Java】 【VulnHub靶场复现】【面试分析】 🎉点赞➕评论➕收藏 …...
黑暗模式适配的实现)
Android Q(10)黑暗模式适配的实现
一、引言 随着 AndroidQ(10)的发布,黑暗模式成为了系统级别的特性。为了满足用户在不同环境下的使用需求,应用程序需要及时进行黑暗模式的适配。本文将详细介绍如何在 AndroidQ(10)上实现黑暗模式的适配&a…...
【git】git使用手册
目录 一 初始化 1.1 账号配置 1.2 ssh生成 1.2.1 配置ssh 1.2.2 测试SSH 1.3 初始化本地仓库并关联远程仓库 二 使用 2.1 上传 2.2 拉取 三 问题 3.1 关联失败 一 初始化 git的安装很简单,下载后大部分进行下一步完成即可----->地址: git工具下载 1.1 账号配置…...

unity中判断方向 用 KeyVertical ,KeyHorizontal 判断ui物体的 方向
float KeyVertical Input.GetAxis("Vertical"); float KeyHorizontal Input.GetAxis("Horizontal"); // 假设 UI 物体在竖直方向上为 Y 轴,水平方向上为 X 轴 Vector2 direction new Vector2(KeyHorizontal, KeyVertical); if (direction…...

前端a4纸尺寸转像素尺寸
前端必备工具推荐网站(免费图床、API和ChatAI等实用工具): http://luckycola.com.cn/ 一、a4纸张有多大 A4纸的尺寸是210mm297mm,也就是21.0cm29.7cm, A4纸尺寸转屏幕像素尺寸和屏幕分辨率有关,首先1英寸2.54cm, 如果屏幕DPI分辨率为72像素/英寸,换算一下ÿ…...

Android 中 调试和减少内存错误
Android 中 调试和减少内存错误 ASan 概述 官网连接: https://developer.android.com/ndk/guides/asan?hlzh-cn ASan API 27开始HWASan(替换AScan) 从 NDK r21 和 Android 10(API 级别 29)开始适用于 64 位 Arm 设…...

证券市场概述
证券市场 证券市场参与者证券发行市场(一级市场)证券发行方式(按发行对象)证券发行方式(按有无中介)证券交易市场(二级市场)证券交易所场外交易市场(店头市场、柜台市场&…...

什么是数据结构
一、什么是数据结构 1.数据结构研究计算机数据间的关系 2.包括数据的逻辑结构和储存结构及其操作 数据的逻辑结构:表示数据运算之间的抽象关系 按每个元素可能具有的直接前趋数和后继数将逻辑结构分为“线性结构”和“非线性结构”两大类 数据的储存结构&#…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...
