【20230211】【剑指1】搜索与回溯算法II
树的子结构
递归思维:对称性递归
什么是对称性递归?就是对一个对称的数据结构(这里指二叉树)从整体的对称性思考,把大问题分解成子问题进行递归,即不是单独考虑一部分(比如树的左子树),而是同时考虑对称的两部分(左右子树),从而写出对称性的递归代码。
题型分类:
可以用对称性递归解决的二叉树问题大多是判断性问题(bool类型函数),这一类问题又可以分为以下两类:
1、不需要构造辅助函数。这一类题目有两种情况:第一种是单树问题,且不需要用到子树的某一部分(比如根节点左子树的右子树),只要利用根节点左右子树的对称性即可进行递归。第二种是双树问题,即本身题目要求比较两棵树,那么不需要构造新函数。
2、需要构造辅助函数。这类题目通常只用根节点子树对称性无法完全解决问题,必须要用到子树的某一部分进行递归,即要调用辅助函数比较两个部分子树。形式上主函数参数列表只有一个根节点,辅助函数参数列表有两个节点。
思路:
此题与572. 另一棵树的子树非常相似,但判断方式不一样。
子结构要么是它本身,要么在它的左子树里面,要么在它的右子树里面。
a) 所以在isSubStructure函数里面要判断是A自身,还是A的左边或右边与B对应 ;
return compare(A, B) || isSubStructure(A->left, B) || isSubStructure(A->right, B);
b) 每次如果匹配失败,必须让B从头开始匹配,而不是直接单层递归compare(A->left,B)||compare(A->right,B),因为此时的B可能是上一层递归传过来的B->next,并不是B真正的根节点;
在递归第一层的时候要检查B是否为空,如果刚开始B就是空树,那么肯定不是子结构;
compare函数里面需要判断:
a) 当B遍历完了,A也遍历完了或者B遍历完了,A还没遍历完,那么B就是子结构;
b) 当A遍历完了,B还没遍历完,说明B不是子结构;
c) 如果AB都没完,但是当前结点值不想等,那么肯定不是子结构;
d) 此时AB都没完,值也相等,那么接着在compare函数里面找AB对应的左右孩子是否相对应;
class Solution {
public:bool compare(TreeNode* A,TreeNode* B){//如果B遍历完,A还没遍历完,那么B是子结构,或者A和B都正好遍历完(前提是遍历过程中都匹配上)if(B==NULL) return true;//如果A遍历完,B还没完,那么B不是子结构if(A==NULL) return false;//如果两个都不空,节点值不同,那么不是子结构if(A->val!=B->val) return false;//如果现在节点值和子树节点值相同,再分别检查两个的左右孩子return compare(A->left,B->left)&&compare(A->right,B->right);}bool isSubStructure(TreeNode* A, TreeNode* B) {if(B==NULL) return false;if(A==NULL) return false;//要么本身比较,要么是它的左子树,要么是右子树return compare(A,B)||isSubStructure(A->left,B)||isSubStructure(A->right,B);}
};2.二叉树的镜像(翻转二叉树)
将二叉树的左右孩子交换即可
class Solution {
public:TreeNode* mirrorTree(TreeNode* root) {if(root==NULL) return NULL;swap(root->left,root->right);mirrorTree(root->left);mirrorTree(root->right);return root;}
};3.对称的二叉树
其实我们要比较的是两个树(这两个树是根节点的左右子树),所以在递归遍历的过程中,也是要同时遍历两棵树。
class Solution {
public:bool compare(TreeNode* left,TreeNode* right){//首先排除空节点情况if(left==NULL&&right==NULL) return true;else if(left!=NULL&&right==NULL) return false;else if(left==NULL&&right!=NULL) return false;//排除值不同的情况else if(left->val!=right->val) return false;//此时左右节点的数值相同,这时再往下做递归//对于左子树而言 左右中 //对于右子树而言 右左中bool outside=compare(left->left,right->right);bool inside=compare(left->right,right->left);return outside&&inside;}bool isSymmetric(TreeNode* root) {if(root==NULL) return true;return compare(root->left,root->right);}
};相关文章:

【20230211】【剑指1】搜索与回溯算法II
树的子结构递归思维:对称性递归什么是对称性递归?就是对一个对称的数据结构(这里指二叉树)从整体的对称性思考,把大问题分解成子问题进行递归,即不是单独考虑一部分(比如树的左子树),而是同时考…...
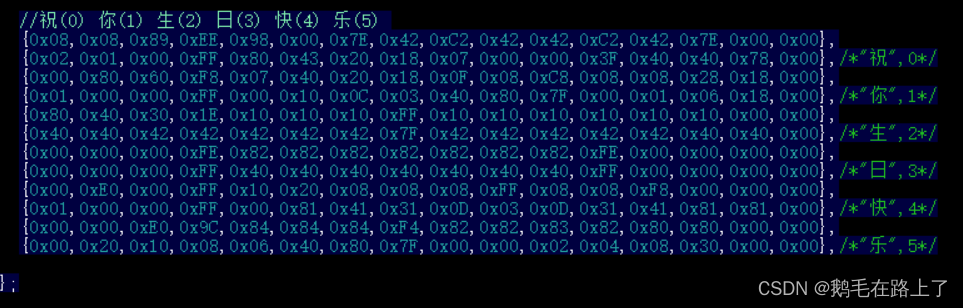
STM32F103C8T6—库函数应用I2C/SPI驱动OLED显示中文、字符串
文章目录1. I2C与SPI通信协议对比2. 四脚OLED与六脚OLED3. I2C驱动OLED显示oled.h & oled.c:汉字取模 & oledfont.h:main.c 显示示例:连线方法:4. SPI驱动OLED显示1. I2C与SPI通信协议对比 I2C(Inter-Integra…...

sql语句要注意的地方及常用查询语句
sql要注意的地方关键字不能被缩写,也不能分行小写大写不敏感,没区别使用缩进提高语句的可读性常用查询语句1.查询所有库SHOW DATABASES;2.选择数据库 use 数据库名USE myemployees;3.查看数据库中所有表show tables4.查看表中的内容 select 字段一&#…...

数组去重、伪数组和真数组的区别以及伪数组如何转换成真数组
1.数组去重 1) 利用数组的indexOf下标属性来查询。 如果找到一个 item,则返回 item 的第一次出现的位置。开始位置的索引为 0。 如果在数组中没找到指定元素则返回 -1。 function unique4(arr) {var newArr []for (var i 0; i < arr.length; i) {i…...

JavaScript内置支持类Array
<!DOCTYPE html> <html> <head> <meta charset"utf-8"> <title>内置支持类Array</title> </head> <body bgcolor"antiquewhite"> <script type"text/javasc…...
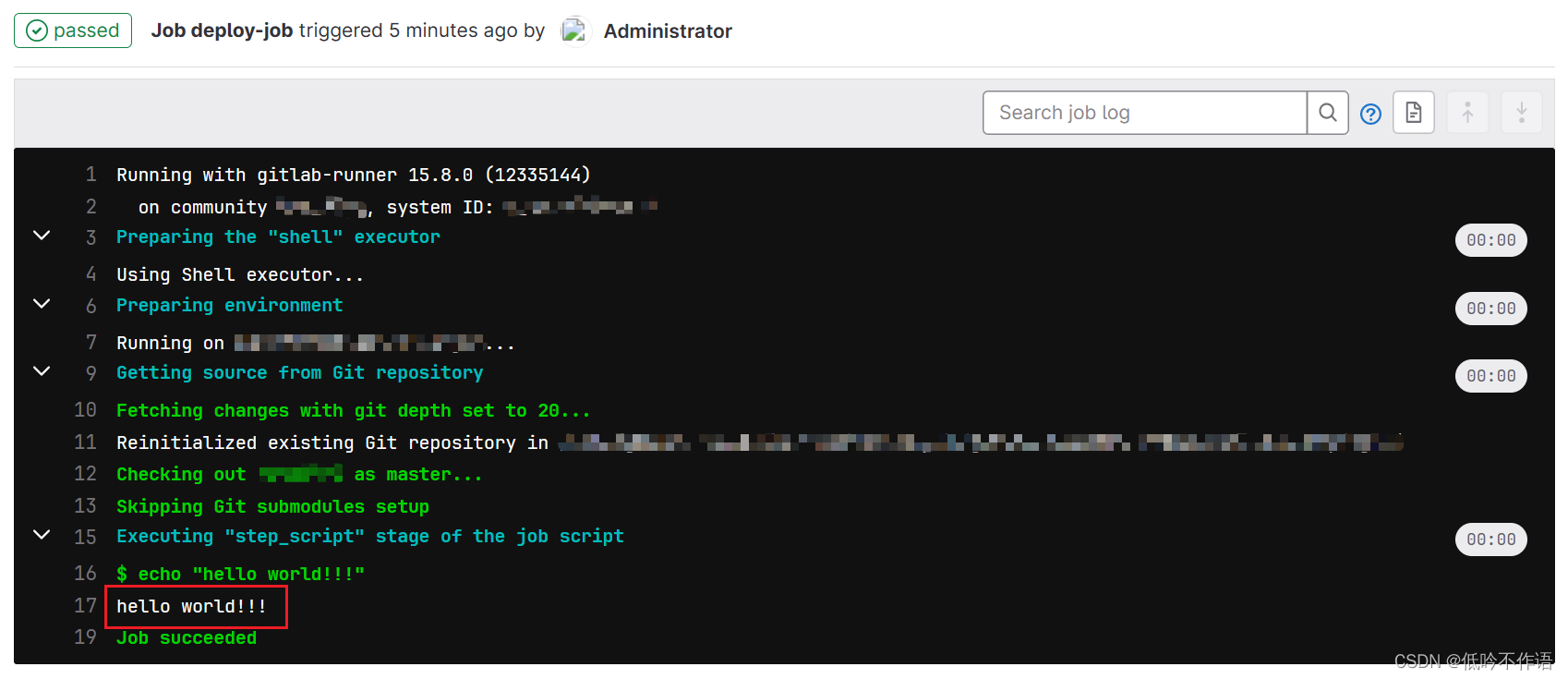
GitLab CI-CD 学习笔记
概述 1. CI/CD CI(持续集成)指开发人员一天内进行多次合并和提交代码操作,并通过自动化测试,完成构建 CD(持续部署)指每次代码更改都会自动部署到对应环境 CI/CD 结合在一起,可以加快开发团…...
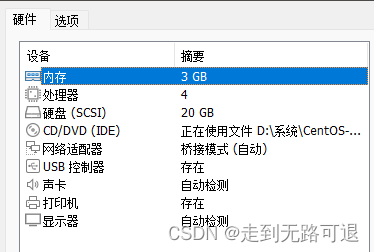
K8S安装
1.创建三台centos虚拟机 使用的官方最小镜像安装 CentOS-7-x86_64-Minimal-1804.iso 建议最小硬件配置:2核CPU、2G内存、20G硬盘 master配置详情 node1和node2配置详情 三台虚拟机在安装centos的时候在网络IPV4指定DHCP,配置IPV4固定地址,保证可以访问…...
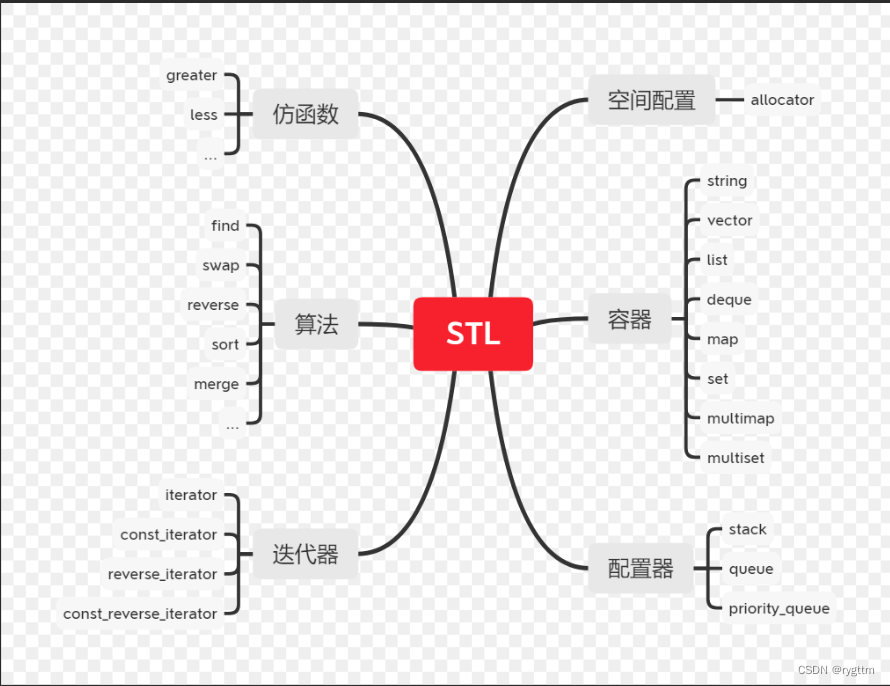
【C++】模板初阶STL简介
今天,你内卷了吗? 文章目录一、泛型编程二、函数模板(显示实例化和隐式实例化)1.函数模板格式2.单参数模板3.多参数模板4.模板参数的匹配原则三、类模板(没有推演的时机,统一显示实例化)1.类模…...
备战蓝桥杯第一天【二分查找无bug版】
🌹作者:云小逸 📝个人主页:云小逸的主页 📝Github:云小逸的Github 🤟motto:要敢于一个人默默的面对自己,强大自己才是核心。不要等到什么都没有了,才下定决心去做。种一颗树,最好的时间是十年前…...

Java集合中的Map
MapMap接口键 值 对存储键不能重复,值可以重复Map三个实现类的存储结构HashMap:Hash表链表红黑树结构 线程不安全TreeMap: 底层红黑树实现HashTable:hash表链表红黑树 线程安全HashMapHashMap常用方法HashMap<String,String>…...

【java】springboot项目启动数据加载内存中的三种方法
文章目录一、前言二、加载方式2.1、 第一种:使用PostConstruct注解(properties/yaml文件)。2.2、 第二种:使用Order注解和CommandLineRunner接口。2.3、 第三种:使用Order注解和ApplicationRunner接口。三、代码示例3.…...
【GO】29.go-gin支持ssl/tls,即https示例
本文为演示采用自签名证书一.生成证书通过openssl工具生成证书1.1 安装opensslmacos通过brew安装brew install openssl1.2 生成跟证书私钥openssl genrsa -out ca.key 40961.3 准备配置文件vim ca.conf内容如下[ req ] default_bits 4096 distinguished_name req_disti…...

逻辑仿真工具VCS的使用-Makefile
Gvim写RTL code,VCS仿真,Verdi看波形,DC做综合下约束,Primetime做STA,Spyglass做异步时序分析。 VCS全称Verilog Computer Simulation ,VCS是逻辑仿真EDA工具的编译源代码的命令。要用VCS做编译仿…...

信息系统安全技术
一、信息安全的有关概念 1. 属性2. 四个安全层次※3. 信息安全保护等级※4. 安全保护能力的等级※ 二、信息加密、解密与常用算法 1. 对称加密2. 非对称加密3. Hash函数4. 数字签名5. 认证 三、信息系统安全 1. 计算机设备安全2. 网络安全3. 操作系统安全4. 数据库安全5. 应用系…...
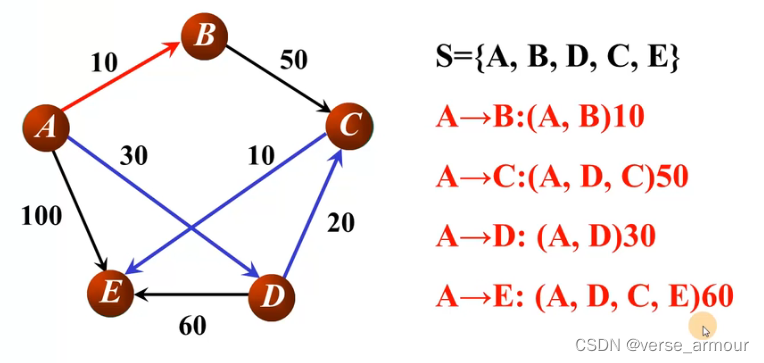
【数据结构】最小生成树(Prim算法,普里姆算法,普利姆)、最短路径(Dijkstra算法,迪杰斯特拉算法,单源最短路径)
文章目录前置问题问题解答一、基础概念:最小生成树的定义和性质(1)最小生成树(Minimal Spanning Tree)的定义(2)最小生成树(MST)的性质二、如何利用MST性质寻找最小生成树…...
)
Session与Cookie的区别(一)
从我刚开始学程序时这一题就常出现在面试考题里,一直到现在都还是能看见这个问题。 这个问题重要吗?我觉得蛮重要的。因为 Session 所代表的是「状态」,如果没有了状态,一大堆功能都会失效。 对于工程师来说必须去理解什么是 Sess…...

【Java】重载和重写的区别
重载(Overload) 在同一个类中,同名的方法如果有不同的参数列表(参数类型不同、参数个数不同甚至是参数顺序不同)则视为重载。同时,重载对返回类型没有要求,可以相同也可以不同,但不能通过返回类型是否相同…...

AcWing 第 90 场周赛
目录A、首字母大写B、找数字C、构造字符串A、首字母大写 原题链接:AcWing 4806. 首字母大写 签到题。 #include <bits/stdc.h>using namespace std;int main() {ios::sync_with_stdio(false);cin.tie(nullptr);string s;cin >> s;s[0] toupper(s[0]);…...

刚刚,体验了一把Bing chat很爽
文章目录刚刚,体验了一把Bing chat很爽你能做啥?与chatgpt有什么不同?以下是Bingchat的 10个新功能1⃣️在网上搜索结果2⃣️摘要链接3⃣️对话助手4⃣️向您发送实际信息,正确的链接5⃣️在单个查询中执行多个搜索6⃣️玩冒险游戏…...

牛客网Python篇数据分析习题(二)
1.现有一个Nowcoder.csv文件,它记录了牛客网的部分用户数据,包含如下字段(字段与字段之间以逗号间隔): Nowcoder_ID:用户ID Level:等级 Achievement_value:成就值 Num_of_exercise&a…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

基于stm32F10x 系列微控制器的智能电子琴(附完整项目源码、详细接线及讲解视频)
注:文章末尾网盘链接中自取成品使用演示视频、项目源码、项目文档 所用硬件:STM32F103C8T6、无源蜂鸣器、44矩阵键盘、flash存储模块、OLED显示屏、RGB三色灯、面包板、杜邦线、usb转ttl串口 stm32f103c8t6 面包板 …...

深度解析云存储:概念、架构与应用实践
在数据爆炸式增长的时代,传统本地存储因容量限制、管理复杂等问题,已难以满足企业和个人的需求。云存储凭借灵活扩展、便捷访问等特性,成为数据存储领域的主流解决方案。从个人照片备份到企业核心数据管理,云存储正重塑数据存储与…...

Yii2项目自动向GitLab上报Bug
Yii2 项目自动上报Bug 原理 yii2在程序报错时, 会执行指定action, 通过重写ErrorAction, 实现Bug自动提交至GitLab的issue 步骤 配置SiteController中的actions方法 public function actions(){return [error > [class > app\helpers\web\ErrorAction,],];}重写Error…...

Springboot 高校报修与互助平台小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,高校报修与互助平台小程序被用户普遍使用,为…...
MeanFlow:何凯明新作,单步去噪图像生成新SOTA
1.简介 这篇文章介绍了一种名为MeanFlow的新型生成模型框架,旨在通过单步生成过程高效地将先验分布转换为数据分布。文章的核心创新在于引入了平均速度的概念,这一概念的引入使得模型能够通过单次函数评估完成从先验分布到数据分布的转换,显…...

【论文解读】MemGPT: 迈向为操作系统的LLM
1st author: Charles Packer paper MemGPT[2310.08560] MemGPT: Towards LLMs as Operating Systems code: letta-ai/letta: Letta (formerly MemGPT) is the stateful agents framework with memory, reasoning, and context management. 这个项目现在已经转化为 Letta &a…...
