算法沉淀 —— 深度搜索(dfs)
算法沉淀 —— 深度搜索(dfs)
- 一、计算布尔二叉树的值
- 二、求根节点到叶节点数字之和
- 三、二叉树剪枝
- 四、验证二叉搜索树
- 五、二叉搜索树中第K小的元素
一、计算布尔二叉树的值
【题目链接】:2331. 计算布尔二叉树的值
【题目】:

【分析】:
在确定一颗二叉树的布尔值前,我们需要先得到左子树、右子树的结果(0/1)。如果左子树、右子树不是叶子节点,显然这是一个递归子问题(将求左子树、右子树的布尔值);
最后就是根据root的值来判断对左/右子树结果的操作(如果是2,按位或;否则为按位与)
【代码实现】:
class Solution {
public:bool evaluateTree(TreeNode* root) {if(root->left == nullptr && root->right == nullptr)return root->val;//完成二叉树保证如果非叶子节点,则左右子树都不为空bool ansL = evaluateTree(root->left);//递归处理左子树bool ansR = evaluateTree(root->right);//递归处理右子树return root->val == 2 ? ansL | ansR : ansL & ansR;}
};
二、求根节点到叶节点数字之和
【题目链接】:129. 求根节点到叶节点数字之和
【题目】:

【分析】:
根节点到叶节点数字之和,显然如果当前节点为叶子节点,此时直接返回结果;否则需要得到当前路径之前路径和(假设为prev),此时当前路径数字和为root->val + prev*10。此时在重复上述过程,如果时叶子节点,直接返回结果;否则转化为递归子问题求解(左子树、右子树只有非空,都有结果)
由于根节点到叶节点的路径可能存在多条,每一条路径都存在一个结果。所以这里我们可以定义一个全局变量来记录最后的累计结果。(具体看代码)
【代码实现】:
class Solution {
public:int sum = 0;int sumNumbers(TreeNode* root) {int prev = 0;_sumNumbers(root, 0);//prev用于记录当前节点前的路径和return sum;}void _sumNumbers(TreeNode* root, int prev){prev = prev * 10 + root->val;//还是使用prev来保存当前路径数字和if(root->left)//左子树非空,必然存在结果,转化成递归子问题求解_sumNumbers(root->left, prev);if(root->right)//右子树非空,同上_sumNumbers(root->right, prev);if(root->left == nullptr && root->right == nullptr)//叶子节点, 累加当前路径和sum += prev;}
};
三、二叉树剪枝
【题目链接】:814. 二叉树剪枝
【题目】:

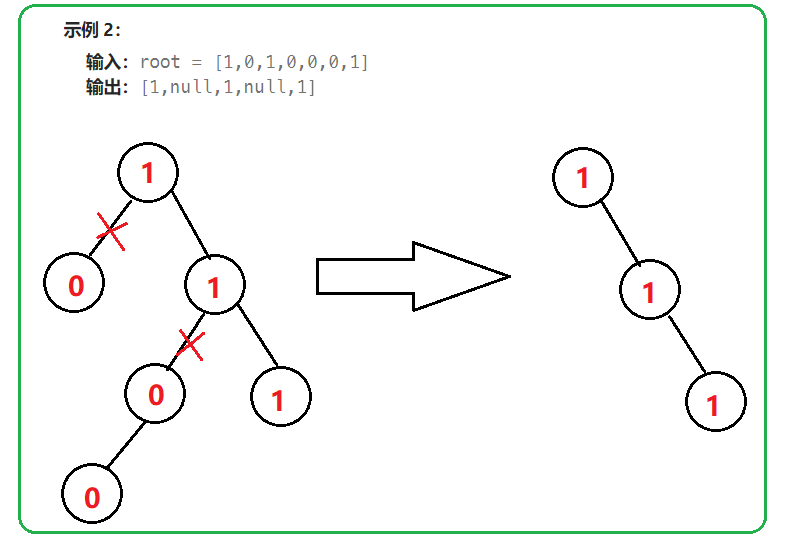
【分析】:
本题中,我们可以采用二叉树后序遍历的思想。先对左子树、右子树分别进行剪枝操作。此时左/右子树中有两种结果:非空、非空(此时子树已经进行了剪枝)。所以此时当前节点必须满足左/右子树均为空,并且根节点为0时,才可继续剪枝。
【代码实现】:
class Solution {
public:TreeNode* pruneTree(TreeNode* root) {//二叉树后序遍历,进行剪枝//对左/右子树剪枝后,左/右子树只有两种结果: 为空、剪完枝非空。if(root == nullptr)return nullptr;root->left = pruneTree(root->left);//对左子树剪枝root->right = pruneTree(root->right);//右子树剪枝if(root->left == nullptr && root->right == nullptr && root->val == 0){delete root;//笔试建议省略此步,原因在于如果root不是new出来的,会报错root = nullptr;}return root;}
};
四、验证二叉搜索树
【题目链接】:98. 验证二叉搜索树
【题目】:

【分析】:
我们可以利用二叉搜索树中序遍历是升序的性质来判断是否为二叉搜索树。但如何利用呢?
其中一种思路是先用一个数组记录二叉树中序遍历结果,在判断是否为升序。但此时算法的空间复杂度为O(n)。
另一种思路就是使用一个全局遍历(prev)来记录中序遍历的前一个数据,然后转化成当前节点和prev比较(当然还有prev值更新啦)。让后根据左子树、右子树、根节点的结果来判断是否符合AVL树(具体参考代码)
tips:
- prev的初始值需要设置为LLONG_MIN(比INT_MIN小即可)。
【代码实现】:
class Solution {
public:long long prev = LLONG_MIN;//保存中序遍历的前一个节点值bool isValidBST(TreeNode* root) {if(root == nullptr)return true;bool Left = isValidBST(root->left);//记录左子树结果bool cur = false;//记录当前根节点和上一个数据是否符合AVL树性质if(root->val > prev){prev = root->val;cur = true;}bool Right = isValidBST(root->right);//记录左子树结果return Left && Right && cur;}
};
五、二叉搜索树中第K小的元素
【题目链接】:230. 二叉搜索树中第K小的元素
【题目】:

【分析】:
本题意思非常明确,求第k小元素。我们可以通过中序遍历,每遍历一次元素,k–。直到k为1时,返回结果。
这里博主推荐将返回值(定义为ret)、和k的值都设置为全局变量。然后和中序遍历一样,我们只需当k的值为1时,返回结果结果;并且每次遍历k–。
【代码实现】:
class Solution {
public:int count = 0, ret = 0;int kthSmallest(TreeNode* root, int k) {count = k;_kthSmallest(root);return ret;}void _kthSmallest(TreeNode* root){if(root == nullptr || count == 0)return;_kthSmallest(root->left);if(--count == 0)ret = root->val;_kthSmallest(root->right);}
};
相关文章:

算法沉淀 —— 深度搜索(dfs)
算法沉淀 —— 深度搜索(dfs) 一、计算布尔二叉树的值二、求根节点到叶节点数字之和三、二叉树剪枝四、验证二叉搜索树五、二叉搜索树中第K小的元素 一、计算布尔二叉树的值 【题目链接】:2331. 计算布尔二叉树的值 【题目】: …...
)
#设计模式#3.1用做松鼠桂鱼来理解抽象工厂(对象创建型模式)
概念:xx工厂,xx产品 区分 工厂是动作,产品是结果(菜品) 概念:抽象xx,具体xx 区分 抽象产品:“中式菜品” 具体产品:“麻婆豆腐”、“宫保鸡丁” 抽象工厂:“…...

adb基本命令
下载安装 adb 概述: ADB 全称为 Android Debug Bridge,起到调试桥的作用,是一个客户端-服务器端程序。其中客户端是用来操作的电脑,服务端是 Android 设备。 下载地址: Windows版本:https://dl.google.com/android/repository/pl…...

小工具实战-Python实现小工具输出字符串大小写转换、字符串统计、编解码、MD5加密
小工具实战-Python实现小工具输出字符串大小写转换、字符串统计、编解码、MD5加密 学习建议字符串大小写转换实现思路部分代码 字符串统计实现思路部分代码: 字符串编解码实现思路部分代码 字符串MD5加密实现思路部分代码 小工具整体设计设计思路工具完整代码实现输…...

MySQL进阶-----索引的语法与SQL性能分析
目录 前言 一、索引语法 1.SQL语法 2.案例演示 二、SQL性能分析 三、慢查询日志 1.开启日志 2.测试样例 四、profile详情 1.开启profile 2.profile测试SQL语句 五、explain详情 1.语法结构 2.执行顺序示例(id) 3.执行性能示例(type) 前言 本…...

Ansible剧本playbooks详解
一、playbook简介 playbook是ansible用于配置,部署和管理托管主机剧本,通过playbook的详细描述,执行其中一系列tasks,playbook字面意思是剧本,现实中由演员按剧本表演,在ansible中由计算机进行安装&#x…...
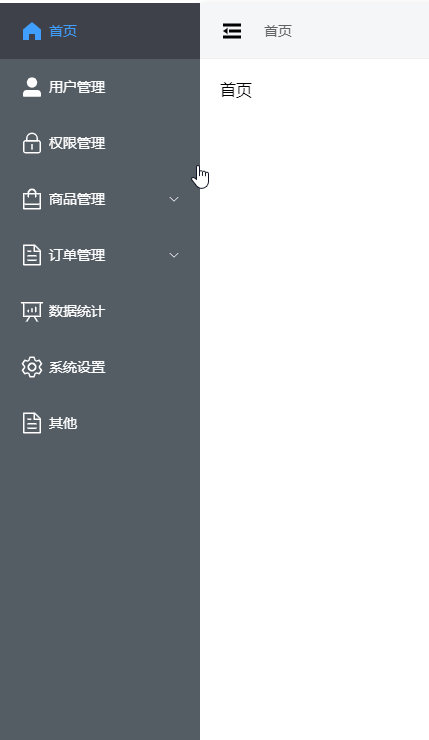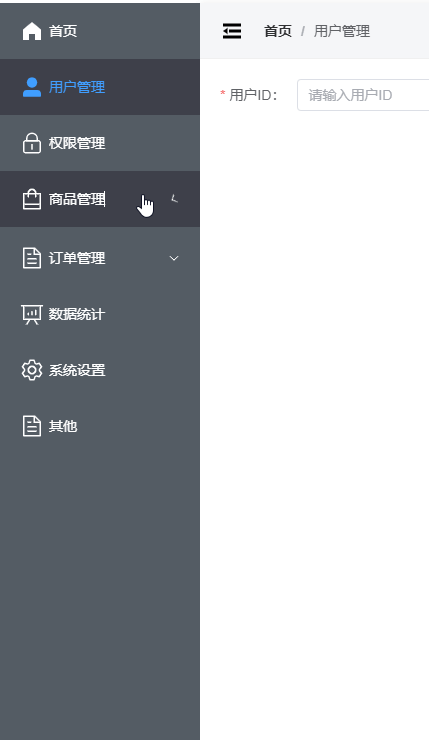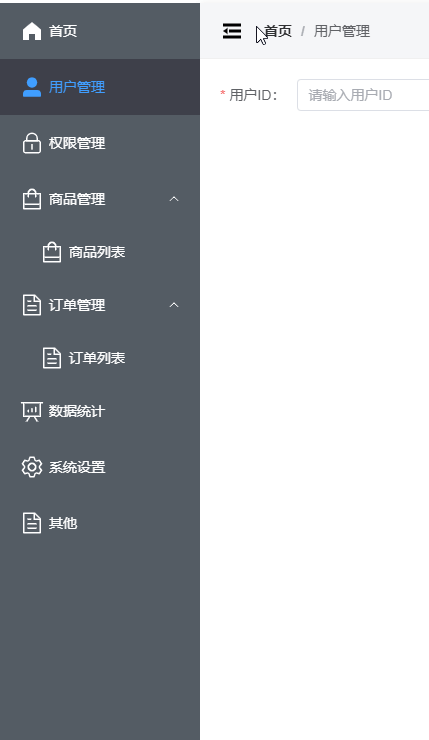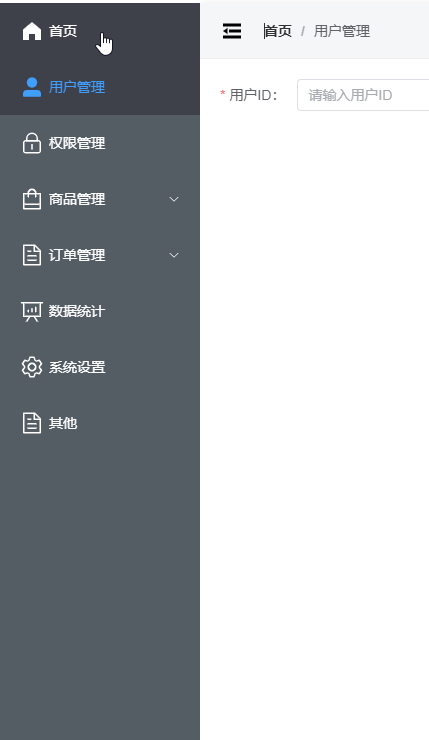
vue3封装Element导航菜单
1. 导航外层布局 AsideView.vue <template><el-menu:default-active"defaultActive"class"my-menu":collapse"isCollapse":collapse-transition"false"open"handleOpen"close"handleClose"><menu…...

字符串的函数
头文件 # include <string.h> 五大函数: strlen()、strcpy、strcat()、strcmp()、strstr() 用法: strlen():计算字符串长度,但不计\0这个字符 #include <string.h> int main() {char arr[] "abcdef"…...
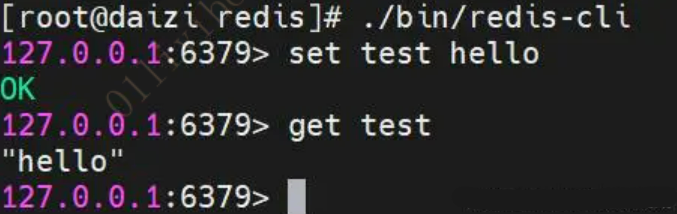
Linux安装redis(基于CentOS系统,Ubuntu也可参考)
前言:本文内容为实操记录,仅供参考! 一、下载并解压Redis 1、执行下面的命令下载redis:wget https://download.redis.io/releases/redis-6.2.6.tar.gz 2、解压redis:tar xzf redis-6.2.6.tar.gz 3、移动redis目录&a…...

ChatGPT引领量化交易革命:AI在金融创新的浪潮中崭露头角
随着科技的飞速发展,金融领域正迎来一场前所未有的创新浪潮。在这场变革中,ChatGPT凭借其卓越的自然语言处理能力和深度学习能力,正引领量化交易进入新时代。 量化交易,作为现代金融领域的一种重要交易方式,依赖于复杂的数学模型和大量的历史数据来制定交易策略。然而,传…...
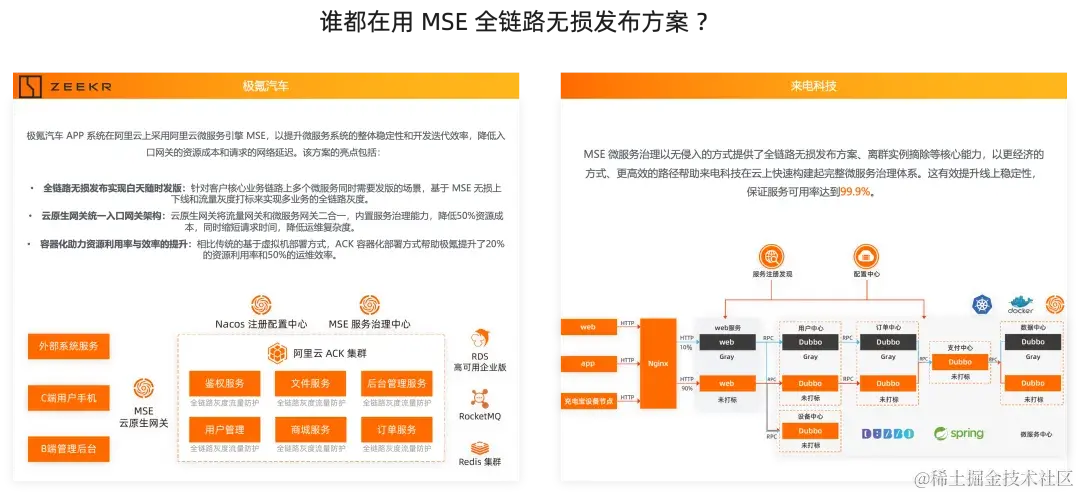
无忧微服务:如何实现大流量下新版本的发布自由
作者:项良、十眠 微服务上云门槛降低,用好微服务才是关键 据调研数据显示,约 70% 的生产故障是由变更引起的。在阿里云上的企业应用如茶百道、极氪汽车和来电等,他们是如何解决变更引起的稳定性风险,实现了在白天高流…...

Halcon3D表面平面度检测-平面差值法
//倾斜平面矫正 https://blog.csdn.net/m0_51559565/article/details/137146179 //平面度和平面缺陷检测,平面矫正法 https://blog.csdn.net/m0_51559565/article/details/137163729前言 通常我们对表面平面度进行检测时,通常使用2种方式。1:…...
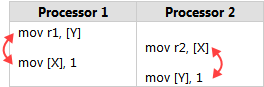
golang 在多线程中避免 CPU 指令重排
发布日期:2024-03-26 16:29:39 起因 golang 的发明初衷便是多线程,是一门专门用于多线程高并发的编程语言。其独创的 GMP 模型在多线程的开发上提供了很大的便利。 现代计算机基本上都是多核 CPU 的结构。CPU 在进行指令运行的时候,为了提高…...

自动化更新包文件--shell脚本
自动化更新包文件--shell脚本 背景手动更包自动化更包 背景 作为一名实施工程师,当然也协助做些测试的工作,当产品功能开发后,研发会将本次迭代涉及的前后端包文件提供过来。有时会因为一些原因研发没法现场开发,那就需要我们配合…...

Vue element-plus 导航栏 [el-menu]
导航栏 [el-menu] Menu 菜单 | Element Plus el-menu有很多属性和子标签,为网站提供导航功能的菜单。 常用标签: 它里面有两个子标签。el-menu-item,它其实就是el-menu每一个里面的item,item就是真实匹配到路由的每个栏目&#…...

数据结构——数组
数组定义: 在计算机科学中,数组是由一组元素(值或变量)组成的数据结构,每个元素有至少一个索引或键来标识。 因为数组内的元素是连续存储的,所以数组中元素的地址,可以通过其索引计算出来。 性…...

python asyncio websockets server
python websocket server在收到接受消息处理完后会默认关闭连接。需要在msg_handler里面加个while true就能一直保持连接了。 start_server websockets.serve(msg_handler, "0.0.0.0", 29967) asyncio.get_event_loop().run_until_complete(start_server) asyncio.…...
视频素材免费网站有哪些?8个视频素材库网站下载推荐
在视频创作领域,选择正确的高质量无水印素材网站能够极大地丰富您的作品,让每一帧都鲜活起来。下面,我们继续为您介绍更多优质的视频素材网站,每一个都是您创作旅程中的宝贵资源。 1. 蛙学府(中国) 集合了…...
ChatGPT与传统搜索引擎的区别:智能对话与关键词匹配的差异
引言 随着互联网的快速发展,信息的获取变得比以往任何时候都更加便捷。在数字化时代,人们对于获取准确、及时信息的需求愈发迫切。传统搜索引擎通过关键词匹配的方式为用户提供了大量的信息,然而,这种机械式的检索方式有时候并不…...
)
xargs后调用bash自定义函数(写该函数文本到脚本, 并引导PATH)
xargs后调用bash自定义函数 需要3步骤,如下 function to_markdown_href_func() { fp$1 #echo $fpecho -e "\n[${fp}](${PREFIX}/${fp})" }BIN/tmp/bin/ F$BIN/to_markdown_href_func.sh mkdir -p $BIN 获得函数to_markdown_href_func的文本 ,写文本到 /tmp/bin/to_ma…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...
