343. 整数拆分(力扣LeetCode)
文章目录
- 343. 整数拆分
- 题目描述
- 动态规划
343. 整数拆分
题目描述
给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k >= 2 ),并使这些整数的乘积最大化。
返回 你可以获得的最大乘积 。
示例 1:
输入: n = 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。
示例 2:
输入: n = 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
提示:
- 2 <= n <= 58
动态规划
下面是代码的详细注释:
class Solution {
public:int integerBreak(int n) {// 初始化一个大小为n+1的动态数组(向量)dp,以0填充// n+1是因为我们想要一个从0到n的索引,包含nvector<int> dp(n+1,0);// 动态规划开始,从2遍历到n,因为我们要求解的是2到n的整数拆分for(int i=2;i<=n;i++){// 内循环,考虑将整数i拆分为两个数:j和i-j// 因为拆分成更多的数可以由这两个数继续拆分得到,所以只需要考虑到i/2for(int j=1;j<=i/2;j++){// dp[i]表示整数i拆分后的最大乘积// 我们检查两种情况:// 1. j * (i - j):直接将i拆分为j和i-j的乘积// 2. j * dp[i - j]:将i拆分为j和拆分(i-j)后得到的最大乘积// 使用max函数来比较并取这两种拆分方式的较大者// 然后再与当前dp[i]的值比较,取较大值更新dp[i]dp[i]=max(dp[i],max(j*(i-j),j*dp[i-j]));}}// 在完成上面的动态规划循环后,dp[n]存储了整数n拆分后的最大乘积// 最后返回该最大乘积return dp[n];}
};
这段代码实现了一个动态规划算法,用于解决给定的正整数n的整数拆分问题,旨在找出拆分后的整数的乘积最大值。代码首先初始化一个动态规划数组dp,大小为n+1以包含从0到n的所有整数拆分的结果,初始值为0。接着,通过双层循环构建出dp数组的每一个元素。外层循环遍历所有待拆分的整数i,内层循环遍历可能的拆分位置j。在内层循环中,通过比较不同拆分方式得到的乘积,来决定最大乘积是直接拆分为j和i-j的乘积,还是拆分为j和拆分i-j后得到的最大乘积,最后更新dp[i]为这些可能中的最大值。动态规划完成后,dp[n]中存储的就是题目要求的整数n拆分后的最大乘积。
相关文章:
)
343. 整数拆分(力扣LeetCode)
文章目录 343. 整数拆分题目描述动态规划 343. 整数拆分 题目描述 给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k > 2 ),并使这些整数的乘积最大化。 返回 你可以获得的最大乘积 。 示例 1: 输入: n 2 输出: 1 解释:…...

Spring面试题系列-3
Spring框架是由于软件开发的复杂性而创建的。Spring使用的是基本的JavaBean来完成以前只可能由EJB完成的事情。然而,Spring的用途不仅仅限于服务器端的开发。从简单性、可测试性和松耦合性角度而言,绝大部分Java应用都可以从Spring中受益。 Spring的属性…...

【比特币】比特币的奥秘、禁令的深层逻辑与风云变幻
导语: 比特币(Bitcoin),这个充满神秘色彩的数字货币,自诞生以来便成为各界瞩目的焦点。它背后所蕴含的Mining机制、禁令背后的深层逻辑以及市场的风云变幻,都让人欲罢不能。今天,我们将深入挖掘比特币的每一个角落&…...
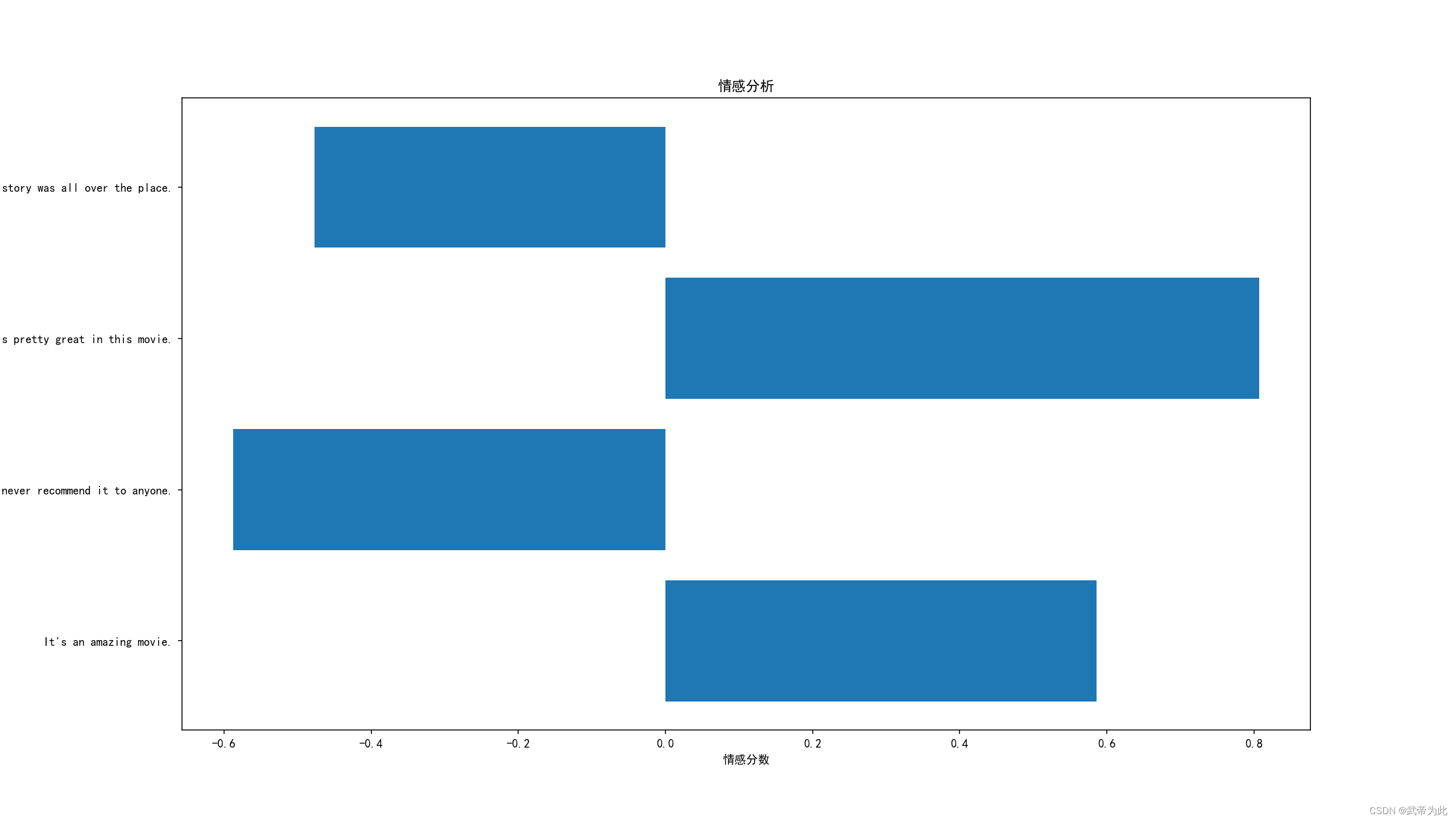
【情感分析概述】
文章目录 一、情感极性分析概述1. 定义2. 情感极性的类别3. 应用场景 二、情感极性分析的技术方法1. 基于规则的方法a. 关键词打分b. 情感词典的使用 2. 基于机器学习的方法a. 监督学习方法b. 深度学习方法 三、Python进行情感极性分析 一、情感极性分析概述 情感极性分析&…...
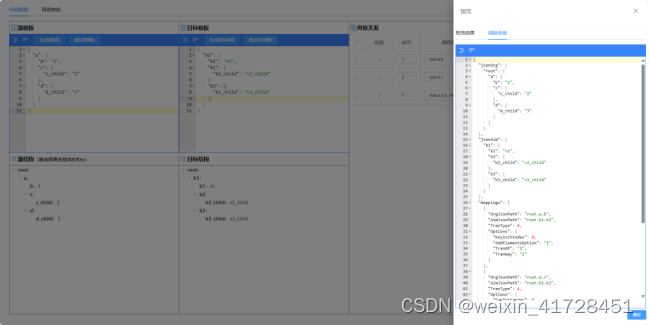
【御控物联】JavaScript JSON结构转换(12):对象To数组——键值互换属性重组
文章目录 一、JSON结构转换是什么?二、核心构件之转换映射三、案例之《JSON对象 To JSON数组》四、代码实现五、在线转换工具六、技术资料 一、JSON结构转换是什么? JSON结构转换指的是将一个JSON对象或JSON数组按照一定规则进行重组、筛选、映射或转换…...
5.6 物联网RK3399项目开发实录-Android开发之U-Boot 编译及使用(wulianjishu666)
物联网入门到项目实干案例下载: https://pan.baidu.com/s/1fHRxXBqRKTPvXKFOQsP80Q?pwdh5ug --------------------------------------------------------------------------------------------------------------------------------- U-Boot 使用 前言 RK U-B…...
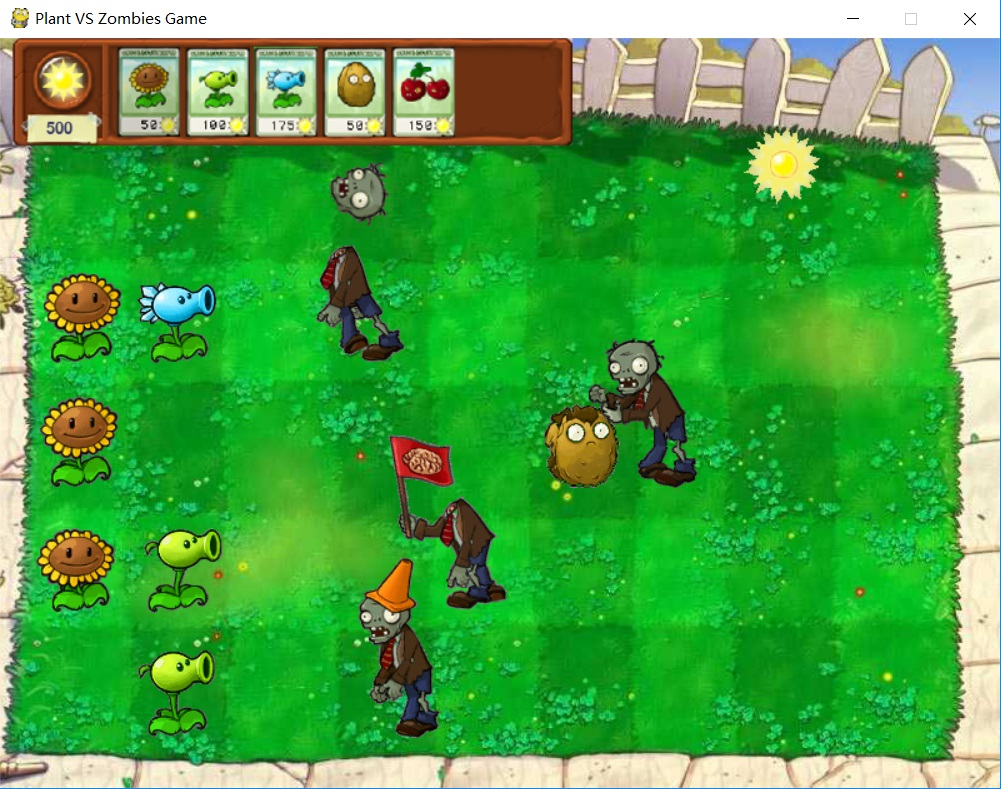
Python版【植物大战僵尸 +源码】
文章目录 写在前面:功能实现环境要求怎么玩个性化定义项目演示:源码分享Map地图:Menubar.py主菜单 主函数:项目开源地址 写在前面: 今天给大家推荐一个Gtihub开源项目:PythonPlantsVsZombies,翻译成中就是…...
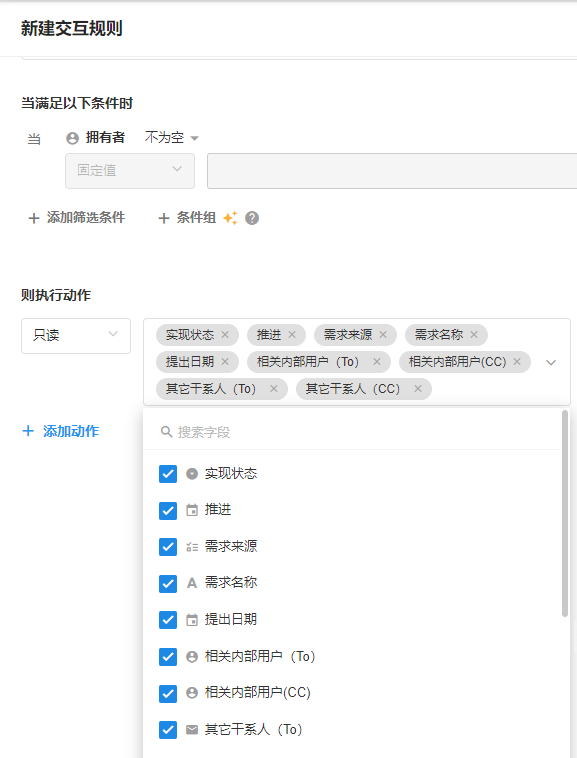
【明道云】如何让用户可以新增但不能修改记录
【背景】 遇到一个需求场景,用户希望新增数据后锁住数据不让更改。 【分析】 在设计表单时直接将字段设置只读是不行的。字段设置只读将会直接让界面上此字段的前端组件不可编辑。包括新增时也无法填入。显然是不符合需求的。 需要既能新增,新增后又不…...
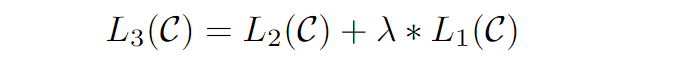
GPT-1原理-Improving Language Understanding by Generative Pre-Training
文章目录 前言提出动机模型猜想模型提出模型结构模型参数 模型预训练训练的目标训练方式训练参数预训练数据集预训练疑问点 模型微调模型输入范式模型训练微调建议微调疑问点 实验结果分析GPT-1缺陷 前言 首先想感慨一波 这是当下最流行的大模型的的开篇之作,由Op…...

web3.0入门及学习路径
Web3是指下一代互联网的演进形式,它涉及一系列技术和理念,旨在实现去中心化、开放、透明和用户主导的互联网体验。Web3的目标是赋予用户更多的控制权和数据所有权,并通过区块链、加密货币和分布式技术来实现。 一、特点 去中心化࿱…...

MATLAB 自定义中值滤波(54)
MATLAB 自定义中值滤波(54) 一、算法介绍二、算法实现1.原理2.代码一、算法介绍 中值滤波,是一种常见的点云平滑算法,改善原始点云的数据质量问题,MATLAB自带的工具似乎不太友好,这里提供自定义实现的点云中值滤波算法,具体效果如下所示: 中值滤波前: 中值滤波后:…...
harmonyOS的客户端存贮
什么是客户端存贮 在harmonyOS中,客户端存贮是指将数据存贮在本地设备以供应用程序使用; 注: 和feaureAblity搭配使用,content上下文的获取依赖该API如下: // 引入: import featureAbility from ohos.ability.featureAbility;// 使用: let content featureAbility.getConten…...

安科瑞智慧安全用电综合解决方案
概述 智慧用电管理云平台是智慧城市建设的延伸成果,将电力物联网技术与云平台的大数据分析功能相结合,实现用电信息的可视化管理,可帮助用户实现安全用电,节约用电,可靠用电。平台支持web,app,微…...

Web 前端性能优化之二:图像优化
1、图像优化 HTTP Archive上的数据显示,网站传输的数据中,60%的资源都是由各种图像文件组成的。 **图像资源优化的根本思想,可以归结为两个字:压缩。**无论是选取何种图像的文件格式,还是针对同一种格式压缩至更小的…...

android——枚举enum
在Kotlin中,枚举(Enum)是一种特殊的类,用于表示固定数量的常量。它允许你定义一组命名的常量值,这些值在程序中具有固定的意义。Kotlin的枚举功能强大,支持多种特性,如伴生对象、构造函数、属性…...

Day54:WEB攻防-XSS跨站Cookie盗取表单劫持网络钓鱼溯源分析项目平台框架
目录 XSS跨站-攻击利用-凭据盗取 XSS跨站-攻击利用-数据提交 XSS跨站-攻击利用-flash钓鱼 XSS跨站-攻击利用-溯源综合 知识点: 1、XSS跨站-攻击利用-凭据盗取 2、XSS跨站-攻击利用-数据提交 3、XSS跨站-攻击利用-网络钓鱼 4、XSS跨站-攻击利用-溯源综合 漏洞原理…...

2024年MathorCup数学建模思路C题思路分享
文章目录 1 赛题思路2 比赛日期和时间3 组织机构4 建模常见问题类型4.1 分类问题4.2 优化问题4.3 预测问题4.4 评价问题 5 建模资料 1 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 2 比赛日期和时间 报名截止时间:2024…...
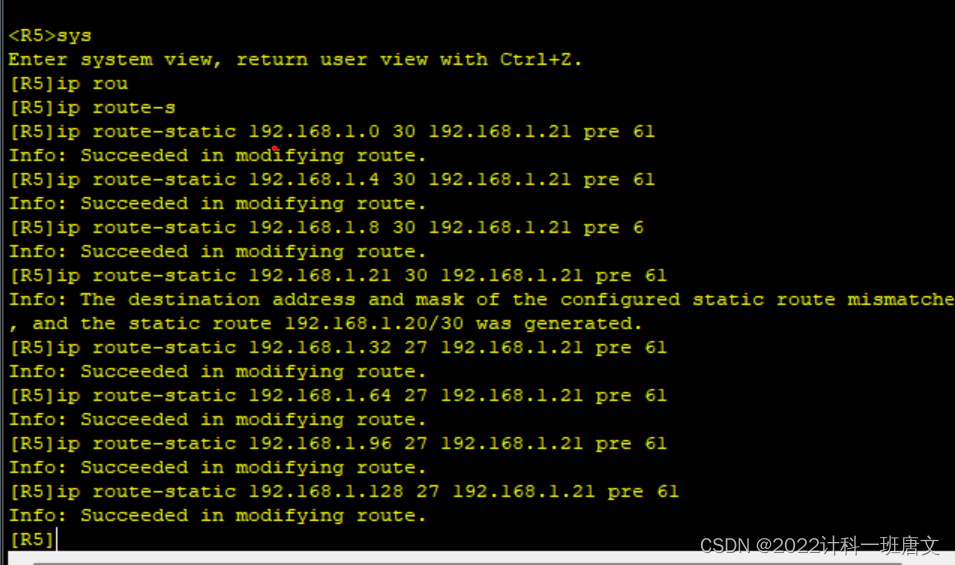
HCIP作业
实验要求: 1、R6为ISP,接口IP地址均为公有地址,该设备只能配置IP地址,之后不能再对其进行任何配置; 2、R1-R5为局域网,私有IP地址192.168.1.0/24,请合理分配; 3、R1、R2、R4&#x…...

如何向sql中插入数据-接上一篇《MySQL数据库的下载和安装以及命令行语法学习》续
接上一篇 《MySQL数据库的下载和安装以及命令行语法学习》续https://blog.csdn.net/tiger_web0/article/details/136903805 在SQL中,要向表中添加数据,您通常使用INSERT INTO语句。 以下是如何使用INSERT INTO语句的基本格式和示例: 基本格式…...

简单的HTML
1.HTML介绍 HTML(HyperText Markup Language,超文本标记语言)是用于创建网页的标准标记语言。它使用一系列的元素来描述网页的结构和内容,包括文本、图像、链接、表格等。 1.1HTML基础结构 HTML文件是一种纯文本文件,由一系列的元素构成。每个元素由一对尖括号<>包围,…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...

深入解析光敏传感技术:嵌入式仿真平台如何重塑电子工程教学
一、光敏传感技术的物理本质与系统级实现挑战 光敏电阻作为经典的光电传感器件,其工作原理根植于半导体材料的光电导效应。当入射光子能量超过材料带隙宽度时,价带电子受激发跃迁至导带,形成电子-空穴对,导致材料电导率显著提升。…...
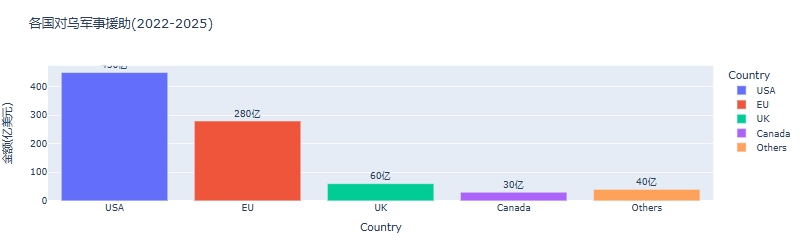
python可视化:俄乌战争时间线关键节点与深层原因
俄乌战争时间线可视化分析:关键节点与深层原因 俄乌战争是21世纪欧洲最具影响力的地缘政治冲突之一,自2022年2月爆发以来已持续超过3年。 本文将通过Python可视化工具,系统分析这场战争的时间线、关键节点及其背后的深层原因,全面…...
