【数据结构】非线性结构---二叉树
1、树
1.1 树的相关概念
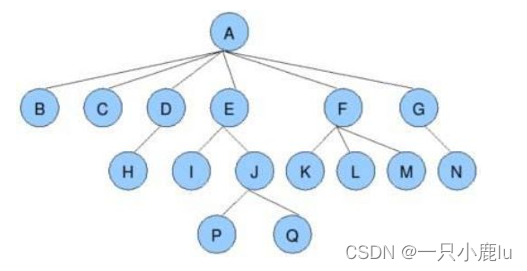
节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的为6
叶节点或终端节点:度为0的节点称为叶节点; 如上图:B、C、H、I...等节点为叶节点
非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G...等节点为分支节点
双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B的父节点
孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节点
兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点
树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6 节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
树的高度或深度:树中节点的最大层次; 如上图:树的高度为4
堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点
节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
森林:由m(m>0)棵互不相交的树的集合称为森林;
1.2 树的表示
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,既然保存值域,也要保存结点和结点之间 的关系,实际中树有很多种表示方式如:双亲表示法,孩子表示法、孩子双亲表示法以及孩子兄弟表示法 等。其中最常用的是孩子兄弟表示法。
typedef int DataType;struct Node{struct Node* _firstChild1; // 第一个孩子结点 struct Node* _pNextBrother; // 指向其下一个兄弟结点 DataType _data; // 结点中的数据域 };2.二叉树概念及结构
2.1概念
一棵二叉树是结点的一个有限集合,该集合:
1. 或者为空
2. 由一个根节点加上两棵别称为左子树和右子树的二叉树组成
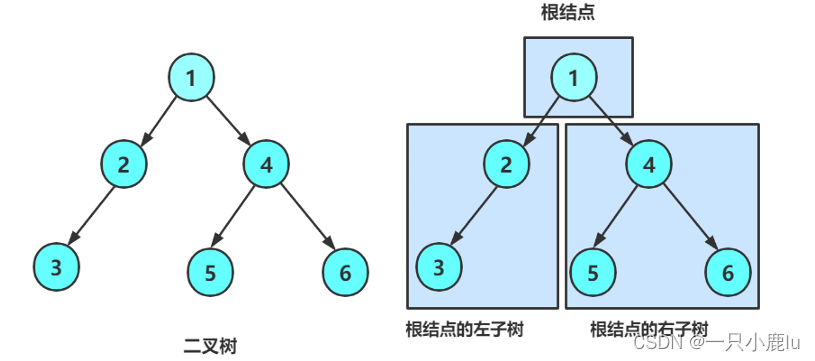
1. 二叉树不存在度大于2的结点
2. 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
2.2特殊的二叉树
1. 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是 说,如果一个二叉树的层数为K,且结点总数是,则它就是满二叉树。
满二叉树:每一层都是满的,结点个数为2^h-1
2. 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K 的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对 应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
完全二叉树:前n-1层都是满的,最后一层可以不满,但是从左到右是连续的,结点范围[2^(h-1), 2^h-1]
2.3 二叉树的性质
1. 若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有 个结点2^(i-1).
2. 若规定根节点的层数为1,则深度为h的二叉树的最大结点数是2^h-1.
3. 对任何一棵二叉树, 如果度为0其叶结点个数为 n0 , 度为2的分支结点个数为n0=n2+1.
4. 若规定根节点的层数为1,具有n个结点的满二叉树的深度,h= ,则有= . (ps: +1 是log以2 为底,n+1为对数)
5. 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从0开始编号,则对 于序号为i的结点有:
1. 若i>0,i位置节点的双亲序号:(i-1)/2;i=0,i为根节点编号,无双亲节点
2. 若2i+1=n否则无左孩子
3. 若2i+2=n否则无右孩子
3.二叉树的顺序结构及实现
3.1 二叉树的顺序结构
普通的二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结 构存储。现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储,需要注意的是这里的堆和操作系统 虚拟进程地址空间中的堆是两回事,一个是数据结构,一个是操作系统中管理内存的一块区域分段。
3.2 堆的概念及结构
一个集合所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,堆中某个节点的值总是小于或等于其父节点的值是大堆,堆中某个节点的值总是大于或等于其父节点的值是小堆。
3.3 堆的实现
#include "Heap.h"void HPInit(HP* php)
{assert(php);php->a = (Datatype*)malloc(sizeof(Datatype) * 4);if (php->a == NULL){perror("malloc fail");return;}php->size = 0;php->capacity = 4;
}void HPInitArray(HP* php, int* a, int n)
{assert(php);php->a = (Datatype*)malloc(sizeof(Datatype) * n);if (php->a == NULL){perror("malloc fail");return;}php->size = n;php->capacity = n;for (int i = (n - 1 - 1) / 2; i >= 0; i++){AdjustDown(php->a, php->size, i);}
}void HPDestroy(HP* php)
{assert(php);free(php->a);php->a = NULL;php->size = 0;php->capacity = 0;
}void Swap(Datatype* p1, Datatype* p2)
{Datatype tmp = p1;*p1 = *p2;*p2 = tmp;
}//除了child,前面的数据都构成堆
void AdjustUp(Datatype* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] > a[parent])// 大堆{Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}//左右子树都构成大堆或小堆
void AdjustDown(Datatype* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n){if (child + 1 < n && a[child + 1] > a[child])//大堆{++child;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}}void HPPush(HP* php, Datatype x)
{assert(php);if (php->size == php->capacity){Datatype* tmp = (Datatype*)realloc(php->a, sizeof(Datatype)*php->capacity*2);if (tmp == NULL){perror("realloc fail");return;}php->a = tmp;php->capacity *= 2;}php->a[php->size] = x;php->size++;AdjustUp(php->a, php->size - 1);
}void HPPop(HP* php)
{assert(php);assert(!PHEmpty(php));//和最后一个数据交换Swap(&php->a[0], &php->a[php->size - 1]);php->size--;AdjustDown(php->a, php->size - 1, 0);}Datatype HPTop(HP* php)
{assert(php);return php->a[0];
}bool HPEmpty(HP* php)
{assert(php);return php->size == 0;
}int HPSize(HP* php)
{assert(php);return php->size;
}//堆排序--升序--建大堆
void HPSort(int* a, int n)
{建堆--向上调整--O(NlogN)//for (int i = 1; i < n; i++)//{// AdjustUp(a, i);//}//建堆--向下调整--O(N)for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(a, n, i);}//实现排序--O(NlogN)int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);end--;}
}相关文章:

【数据结构】非线性结构---二叉树
1、树 1.1 树的相关概念 节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的为6 叶节点或终端节点:度为0的节点称为叶节点; 如上图:B、C、H、I...等节点为叶节点 非终端节点或分支节点&#…...

【战略前沿】与中国达成生产协议后,飞行汽车即将起飞
【原文】Flying cars edge towards takeoff after Chinese production deal 【作者】Thomas Macaulay 斯洛伐克公司KleinVision签署了一项协议,将大规模生产AirCar。 一辆获得航空认证的飞行汽车向商业化又迈出了一大步。 空中汽车的创造者KleinVision今天宣布出售…...
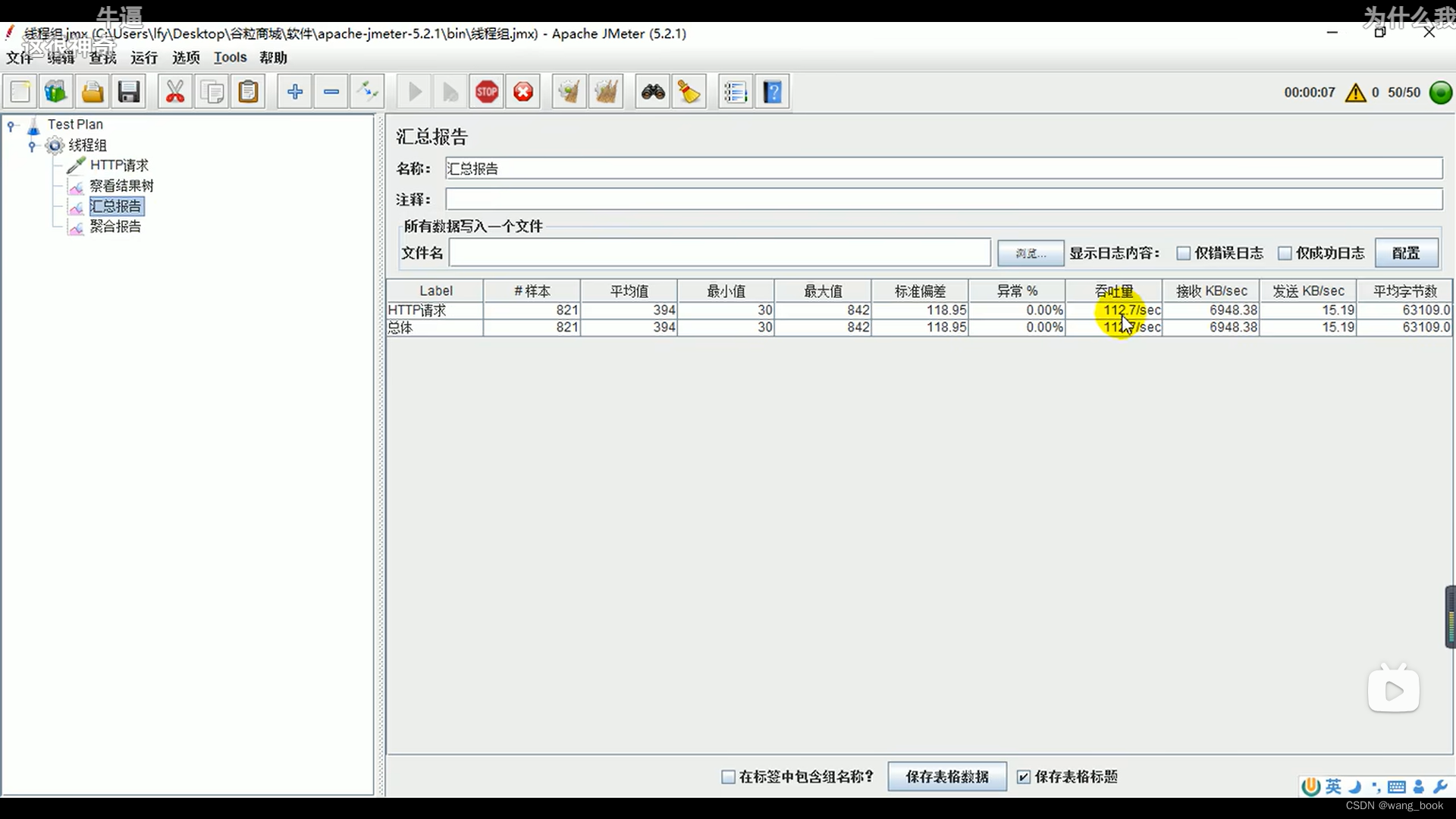
谷粒商城实战(007 压力测试)
Java项目《谷粒商城》架构师级Java项目实战,对标阿里P6-P7,全网最强 总时长 104:45:00 共408P 此文章包含第141p-第p150的内容 简介 安装jmeter 安装jmeter 使用中文 这样写就是200个线程循环100次 一共是2万个请求 介绍线程组 添加请求 可以是htt…...

使用CSS计数器,在目录名称前加上了序号,让目录看起来更加井然有序
目录(Text of Contents缩写为TOC),其实就是一篇文章的概要或简述。这好比,去书店买书,先是被这本书的标题所吸引,而后我们才会,翻开这本书目录,看看这本书主要是在讲些什么ÿ…...

SSH常见运维总结
1 -bash: ssh: command not found 解决办法:"yum install -y openssh-server openssh-clinets" 2 ssh登录时提示:Read from socket failed: Connection reset by peer. 原因:/etc/ssh/下没有ssh*key*文件 解决&…...

uni app 扫雷
闲来无聊。做个扫雷玩玩吧,点击打开,长按标记,标记的点击两次或长按取消标记。所有打开结束 <template><view class"page_main"><view class"add_button" style"width: 100vw; margin-bottom: 20r…...

MATLAB绘制堆叠填充图--巧用句柄
MATLAB绘制堆叠填充图–巧用句柄 目录 MATLAB绘制堆叠填充图--巧用句柄1. 主要原理讲解1.1 主要函数1.2 句柄原理 2. 绘图示例2.1 准备数据2.2 绘制堆叠填充图-使用句柄控制图形属性2.3 设置填充颜色和样式2.4 添加标题和标签2.5 绘图效果 3. 结语 堆叠填充图是一种常见的数据可…...

JQuery的定义
jQuery是一个js库,使用jQuery会比js简单一点 jQuery文件是一个自执行函数 jQuery文件是一个自执行函数 $传递的参数不同,效果也不同: 传递的是匿名函数,那$就是一个入口函数,传递的是一个字符串,那$就…...

【操作系统】FCFS、SJF、HRRN、RR、EDF、LLF调度算法及python实现代码
文章目录 一、先来先服务调度算法(FCFS) 二、短作业优先调度算法(SJF) 三、高响应比优先调度算法(HRRN) 四、轮转调度算法(RR) 五、最早截至时间优先算法(EDF&#…...
Image-Adaptive YOLO for Object Detection in Adverse Weather Conditions(IA-YOLO)
1、总体概述 基于深度学习的目标检测在常规条件的数据集可以获得不错的结果,但是在环境、场景、天气、照度、雾霾等自然条件的综合干扰下,深度学习模型的适应程度变低,检测结果也随之下降,因此研究在复杂气象条件下的目标检测方法…...
Mac电脑Jmeter集成到Jenkins,压测多个接口并生成测试报告
Jenkins支持的JDK版本17、21,通过java -version查看当前JDK版本,确认是否匹配 打开网址https://www.jenkins.io/download 点击下载,选择mac版本 commend空格打开终端,输入安装命令brew install jenkins 安装完成后输入brew servi…...

redis-Hash
一,应用场景 Redis hash 是一个string类型的field和value的映射表,hash特别适合用于存储对象。Set就是一种简化的Hash,只变动key,而value使用默认值填充。 可以将一个Hash表作为一个对象进行存储,表中存放对象的信息。 二,命令 H…...
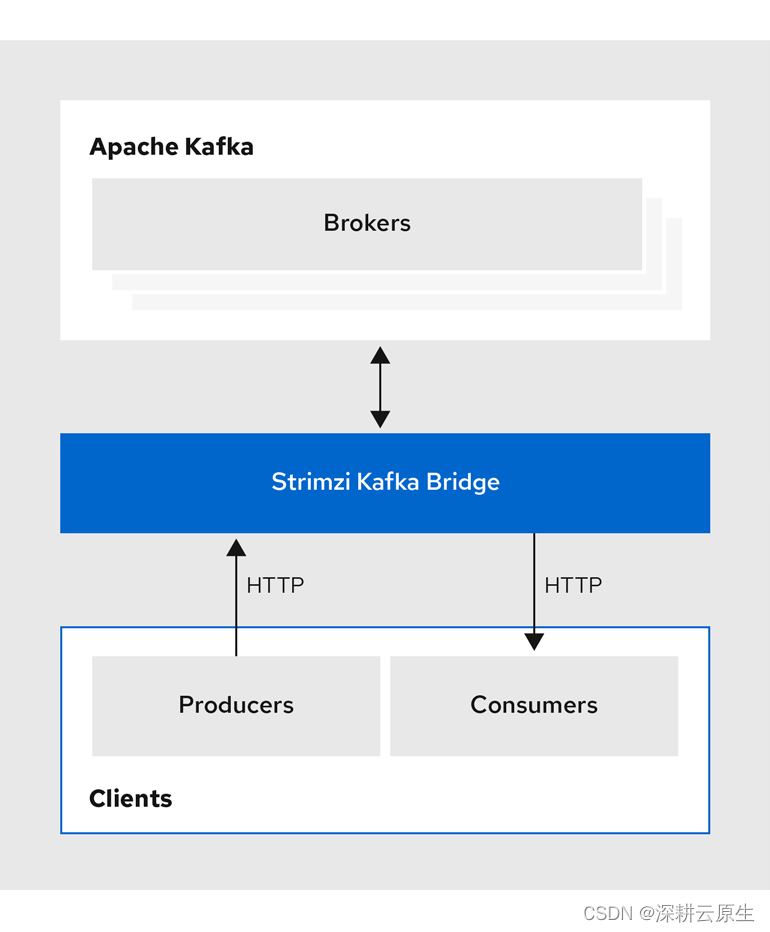
Kubernetes kafka系列 | Strimzi 部署kafka-bridge
Strimzi kafka集群部署直通车 一、kafka bridge 介绍 Kafka Bridge 是 Apache Kafka 生态系统中的一个工具或组件,用于实现 Kafka 与其他系统或协议之间的通信或集成。Kafka 本身是一个分布式事件流平台,广泛用于构建实时数据流水线和流式应用程序。然而…...
AR和VR如何改变客户体验?
How AR and VR are transforming customer experiences? How AR and VR are transforming customer experiences AR和VR如何改变客户体验 AR and VR technology was largely expedited by the past pandemic with at least 93.3 million and 58.9 million users r…...

微信小程序中实现埋点的方法
在小程序开发过程中,埋点是实现数据采集和用户行为分析的重要手段。通过埋点,我们可以获取用户在使用小程序时的各种操作信息,从而更好地了解用户行为特征,优化产品体验。下面将介绍如何在小程序中实现埋点,并通过代码示例进行说明。 一、埋点实现思路 小程序的埋点实现主要依…...

vue记事本渲染以及交互
以下是记事本的源码 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>记事本</title><styl…...

Zookeeper中的脑裂
简单点来说,脑裂(Split-Brain) 就是比如当你的 cluster 里面有两个节点,它们都知道在这个cluster 里需要选举出一个 master。那么当它们两个之间的通信完全没有问题的时候,就会达成共识,选出其中一个作为 master。但是如果它们之间…...

【漏洞复现】金和OA XmlDeal.aspx XXE漏洞
0x01 产品简介 金和数字化智能办公平台(简称JC6)是一款结合了人工智能技术的数字化办公平台,为企业带来了智能化的办公体验和全面的数字化转型支持。同时符合国家信创认证标准,支持组织数字化转型,实现业务流程的数字化、智能化和协同化,提高企业竞争力。 0x02 漏洞概述…...
对比:React 还是 Vue
自己之前的开发栈一直是 Vue,对 Vue 的设计理念及底层实现原理算是颇有了解;随着公司技术迭代,近半年来开始接触&使用 React。 前面写了几篇关于 React 的文章,但大部分都是知识点以及开发过程问题的沉淀总结。 这篇文章想尝…...

ubuntu 20.04 SD 卡分区类型 msdos 改为 GPT 的方法
前言 默认 SD 卡分区是 FAT32 格式,为了用于嵌入式Linux ext4 文件系统,需要改为 ext4 文件系统,但是SD 卡分区类型默认是 msdos 类型,也就是 MBR 类型,不是 GPT 类型。 烧写 ext4 分区表,或者使用 ubuntu…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...
