当前位置： 首页 > news >正文

YOLOv9改进策略 ：主干优化 | 无需TokenMixer也能达成SOTA性能的极简ViT架构 | CVPR2023 RIFormer

news 2026/2/10 20:02:39

   💡💡💡本文改进内容： token mixer被验证能够大幅度提升性能，但典型的token mixer为自注意力机制，推理耗时长，计算代价大，而RIFormers是无需TokenMixer也能达成SOTA性能的极简ViT架构 ，在保证性能的同时足够轻量化。

 💡💡💡RIFormerBlock引入到YOLOv9，多个数据集验证能够大幅度涨点

 改进结构图如下：

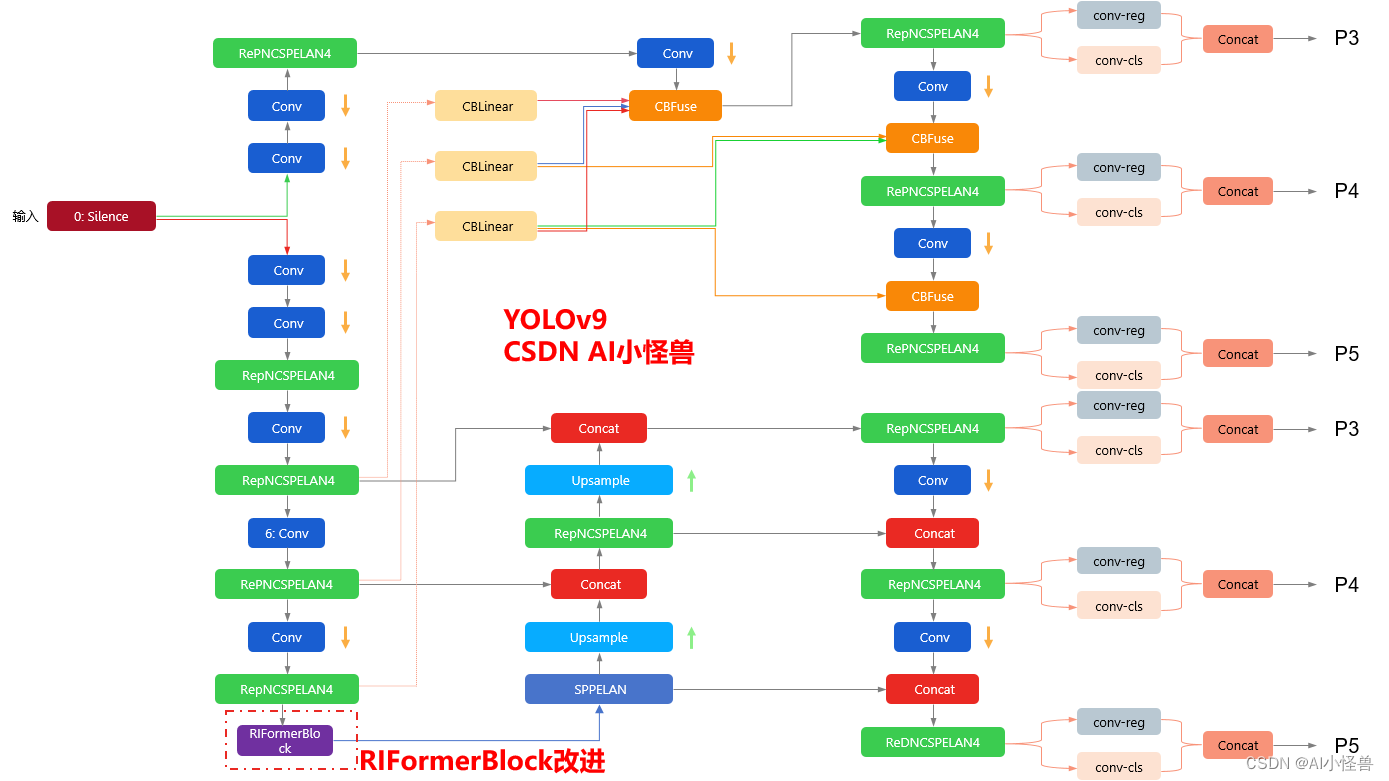
《YOLOv9魔术师专栏》将从以下各个方向进行创新：

【原创自研模块】【多组合点优化】【注意力机制】【卷积魔改】【block&多尺度融合结合】【损失&IOU优化】【上下采样优化 】【SPPELAN & RepNCSPELAN4优化】【小目标性能提升】【前沿论文分享】【训练实战篇】

订阅者通过添加WX:

相关文章：

YOLOv9改进策略 ：主干优化 | 无需TokenMixer也能达成SOTA性能的极简ViT架构 | CVPR2023 RIFormer

💡💡💡本文改进内容： token mixer被验证能够大幅度提升性能，但典型的token mixer为自注意力机制，推理耗时长，计算代价大，而RIFormers是无需TokenMixer也能达成SOTA性能的极简ViT架构 ，在保证性能的同时足够轻量化。 💡💡💡RIFormerBlock引入到YOLOv9，多个数…...

编程日记 2024/4/2 16:52:58

원클릭으로 주류 전자상거래 플랫폼 상품 상세 데이터 수집 및 접속 시연 예제 (한국어판)

클릭 한 번으로 전자상거래 플랫폼 데이터를 캡처하는 것은 일반적으로 웹 페이지에서 정보를 자동으로 추출 할 수있는 네트워크 파충류 기술과 관련됩니다.그러나 모든 형태의 데이터 수집은 해당 웹 사이트의 사용 약관 및 개인 정보 보호 정책 및 현지 법률 및 규정을 준수…...

编程日记 2024/4/2 16:51:57

2024年github开源top100中文

2024年github开源top100中文 动动美丽的小指头点个赞呗，感谢啦！💕💕💕😘😘😘 本文由Butterfly一键发布工具发布 语言star项目名称描述Python45670xai-org/grok-1Grok开源发布Ruby260…...

编程日记 2024/4/2 16:50:56

回收站删除的文件在哪里？专业恢复方法分享（最新版）

“我很想知道我从回收站删除的文件被保存在哪里了呢？我刚刚不小心清空了回收站，现在想将它们恢复，应该怎么操作呢？谁能教教我怎么从回收站恢复文件？” 回收站，作为Windows操作系统中的一个重要组件&#xf…...

编程日记 2024/4/2 16:49:54

什么是工时管理软件？

简而言之，工时管理软件是一种可以帮助管理者跟踪企业员工在项目和任务上花费的时间的软件。然而，工时管理软件不仅是一种收集信息的工具，它还是一种解决方案，使企业能够处理和优化不同的流程和活动，例如工资单、项目预…...

编程日记 2024/4/2 16:48:53

一文解析智慧城市，人工智能技术将成“智”理主要手段

长期以来，有关智慧城市的讨论主要围绕在技术进步方面，如自动化、人工智能、数据的公开以及将更多的传感器嵌入城市以使其更加智能化。实际上，智慧城市是一个关于未来的设想，其重要原因在于城市中存在各种基础设施、政治、地理、财…...

编程日记 2024/4/2 16:43:47

SQLBolt，一个练习SQL的宝藏网站

知乎上有人问学SQL有什么好的网站，这可太多了。 我之前学习SQL买了本SQL学习指南，把语法从头到尾看了个遍，但仅仅是心里有数的程度，后来进公司大量的写代码跑数，才算真真摸透了SQL，知道怎么调优才能最大化…...

编程日记 2024/4/2 16:42:46

TikTok防关联引流系统：全球多账号运营的终极解决方案

tiktok防关联引流系统介绍，tiktok防关联系统是基于tiktok生态研发的效率工具，帮你快速实现tiktok全球多账号运营，系统配备了性能强劲的安卓，防关联智能终端，可一建创建全球多国手机环境，完美满足各类app软件…...

编程日记 2024/4/2 16:39:43

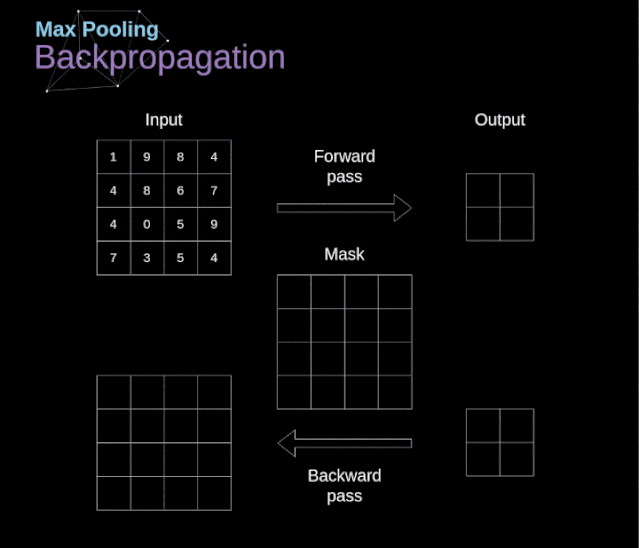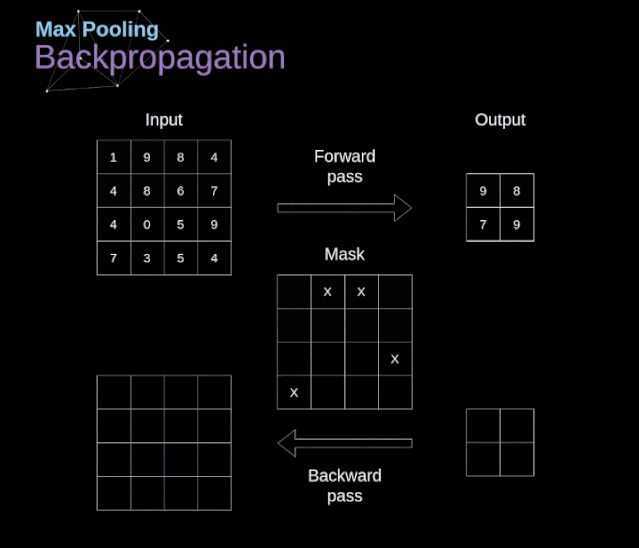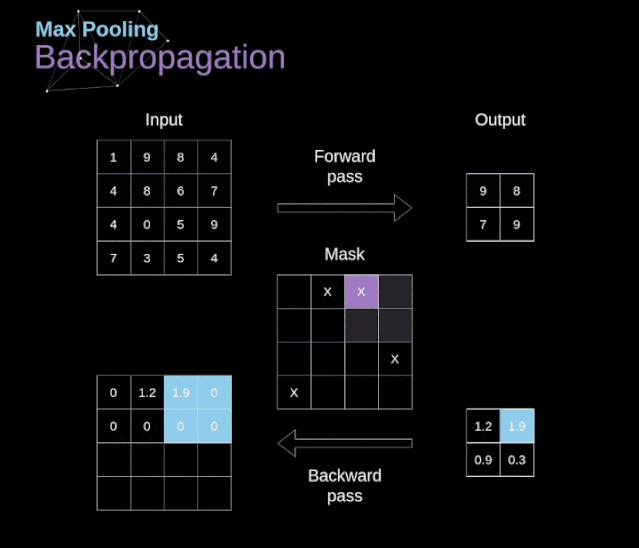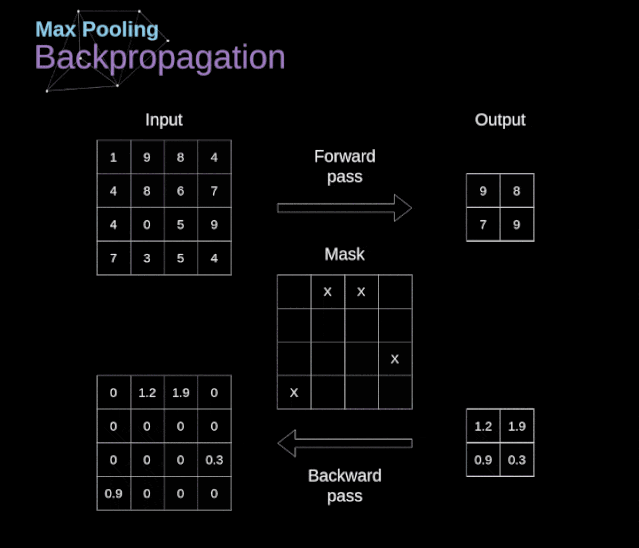
卷积神经网络（CNN）的数学原理解析

文章目录 前言 1、介绍 2、数字图像的数据结构 3、卷积 4、Valid 和 Same 卷积 5、步幅卷积 6、过渡到三维 7、卷积层 8、连接剪枝和参数共享 9、卷积反向传播 10、池化层 11、池化层反向传播 前言 本篇主要分享卷积神经网络（CNN）的数学原理解析&#xf…...

编程日记 2024/4/2 16:36:40

2024年华为OD机试真题-亲子游戏-Java-OD统一考试（C卷）

题目描述： 宝宝和妈妈参加亲子游戏，在一个二维矩阵（N*N）的格子地图上，宝宝和妈妈抽签决定各自的位置，地图上每个格子有不同的糖果数量，部分格子有障碍物。 游戏规则是妈妈必须在最短的时间（每个单位时间只能走一步）到达宝宝的位置，路上的所有糖果都可以拿走，不能走障…...

编程日记 2024/4/2 16:34:37

大模型显存占用分析

kvcache显存占用分析 假设序列输入长度：s，输出长度：n，数据类型以FP16来保存KV cache。 峰值显存占用：b(sn)hl2*24blh(sn) 注：b表示batch size，第一个2表示k/v cache，第二个2表示FP1…...

编程日记 2024/4/2 16:33:36

matlab中旋转矩阵函数

文章目录 matlab里的旋转矩阵、四元数、欧拉角四元数根据两向量计算向量之间的旋转矩阵和四元数欧拉角转旋转矩阵旋转矩阵转欧拉角旋转矩阵转四元数参考链接 matlab里的旋转矩阵、四元数、欧拉角 旋转矩阵dcmR四元数quatq[q0,q1,q2,q3]欧拉角angle[row,pitch,yaw] % 旋转矩阵…...

编程日记 2024/4/2 16:32:34

探讨Spring Boot的自动配置原理

Spring Boot以其简化Spring应用开发和部署的能力而广受欢迎。其中最引人注目的特性之一就是自动配置，它极大地减少了开发者需要手动编写的配置量。在本篇博客中，我们将深入探讨Spring Boot自动配置的工作原理，以及它是如何使得Spring应用的配…...

编程日记 2024/4/2 16:30:32

【LeetCode】热题100 刷题笔记

文章目录 T1 两数之和T49 字母异位词分组常用小技巧 T1 两数之和 链接：1. 两数之和 题目： 【刷题感悟】这道题用两层for循环也能做出来，但我们还是要挑战一下时间复杂度小于 O ( n 2 ) O(n^2) O(n2)的解法，不能因为它是第一道 …...

编程日记 2024/4/2 16:26:27

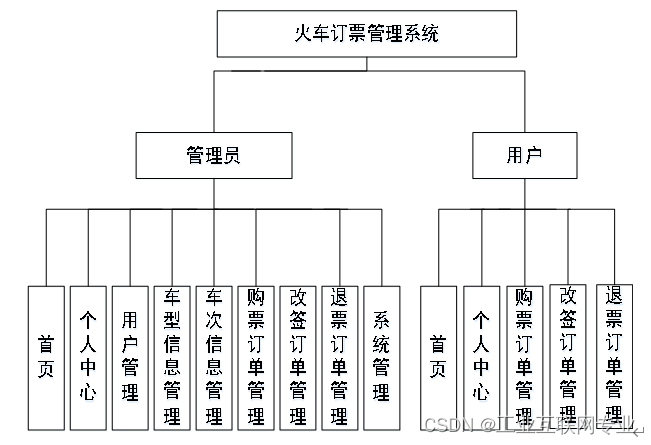
基于springboot+vue+Mysql的火车订票管理系统

开发语言：Java框架：springbootJDK版本：JDK1.8服务器：tomcat7数据库：mysql 5.7（一定要5.7版本）数据库工具：Navicat11开发软件：eclipse/myeclipse/ideaMaven包：…...

编程日记 2024/4/2 16:25:26

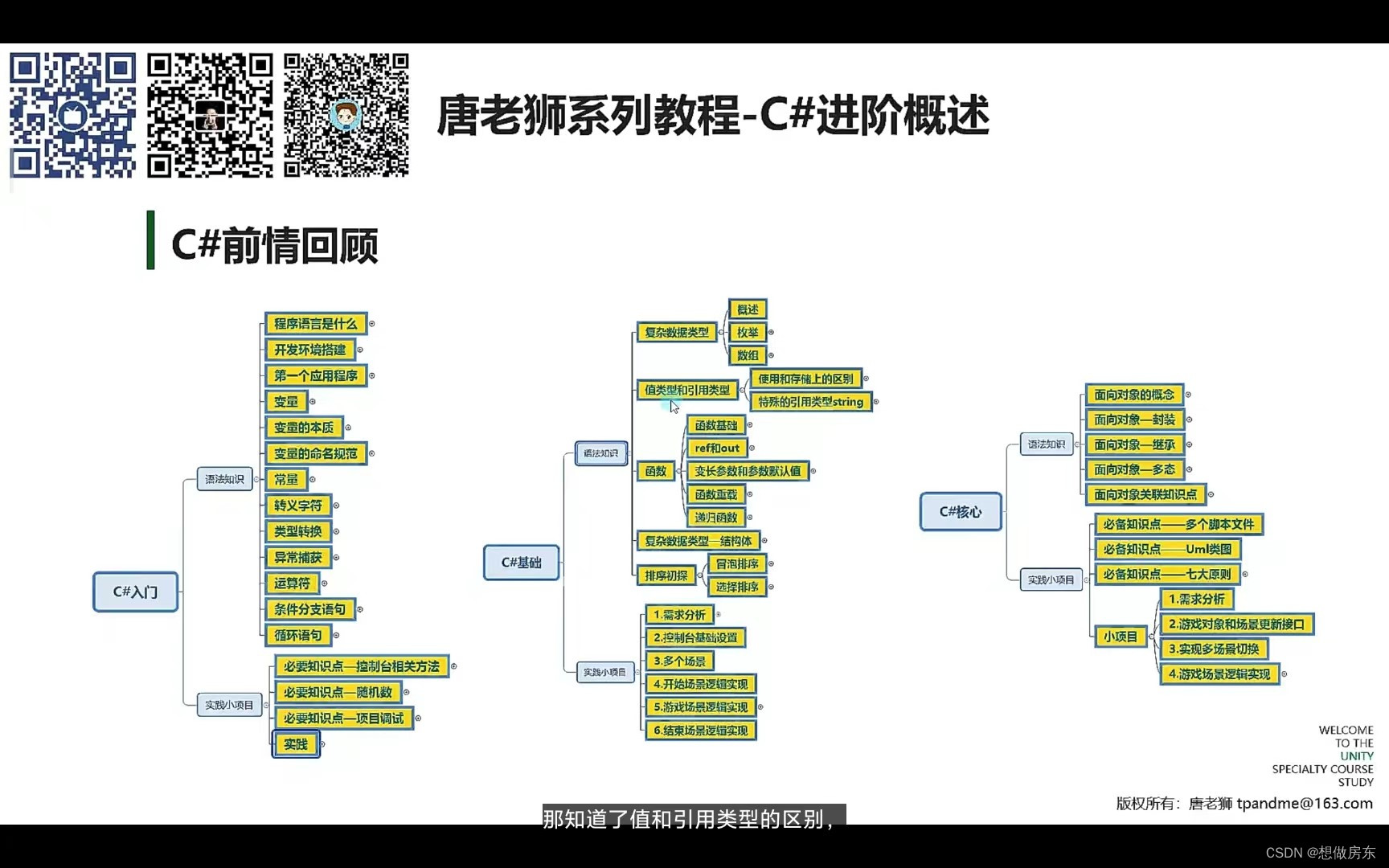
C#学习笔记 面试提要

冒泡 for (int m 0; m < arr.Length; m) { for (int n 0; n < arr.Length - 1 - m; n) { if (arr[n] > arr[n1]) { int temp arr[n]; arr[n] arr[n 1]; arr[n1] temp; } } } 选择 for (int m 0; m < arr.Length; m) { int index 0; for (int n 1; n < …...

编程日记 2024/4/2 16:21:22

Linux用户识别与身份验证命令一览

这些命令在系统管理、用户管理和监控工作中扮演着重要的角色。下面&#xff0c;介绍它们的类型及功能描述&#xff1a; 一、系统信息命令 hostname&#xff1a;此命令用于显示系统的主机名&#xff0c;它代表了系统在网络中的唯一标识。hostname -f&#xff1a;此命令进一步展…...

编程日记 2024/4/2 16:17:18

【Linux】GCC编译器（七）

文章目录 初步了解安装 GCC编译第一个程序编译选项 初步了解 GCC是GNU Compiler Collection的缩写&#xff0c;是一个由GNU项目开发的编译器集合。 GCC的历史和发展&#xff1a;GCC最初由理查德斯托曼&#xff08;Richard Stallman&#xff09;发起&#xff0c;目的是创建一个…...

编程日记 2024/4/2 16:16:16

【目录整理】（五）

​​​​​Git 基础 Git 详细安装教程文章浏览阅读10w次&#xff0c;点赞9.6k次&#xff0c;收藏1.7w次。Git 是个免费的开源分布式版本控制系统&#xff0c;下载地址为git-scm.com 或者 gitforwindows.org&#xff0c;本文介绍 Git-2.40.0-64-bit.exe 版本的安装方法&#x…...

编程日记 2024/4/2 16:15:15

项目：USB键盘和鼠标的复合设备

我们的复合设备使用一个物理设备就可以完成多个功能。 使用复合设备同时完成USB键盘和鼠标功能&#xff0c;它的主要实现方式有两种&#xff0c; 第一个就是我们将多个设备描述符合并成一个&#xff0c;这个相对比较简单&#xff0c;我们只要根据相应的报告描述符处理数据就可…...

编程日记 2024/4/2 16:14:14

wordpress后台更新后 前端没变化的解决方法

使用siteground主机的wordpress网站&#xff0c;会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后&#xff0c;网站没有变化的情况。 不熟悉siteground主机的新手&#xff0c;遇到这个问题&#xff0c;就很抓狂&#xff0c;明明是哪都没操作错误&#x…...

编程新知 2026/2/9 2:42:46

多云管理“拦路虎”：深入解析网络互联、身份同步与成本可视化的技术复杂度​

一、引言&#xff1a;多云环境的技术复杂性本质​​ 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时&#xff0c;​​基础设施的技术债呈现指数级积累​​。网络连接、身份认证、成本管理这三大核心挑战相互嵌套&#xff1a;跨云网络构建数据…...

编程新知 2026/2/8 16:53:48

golang循环变量捕获问题​​

在 Go 语言中&#xff0c;当在循环中启动协程&#xff08;goroutine&#xff09;时&#xff0c;如果在协程闭包中直接引用循环变量&#xff0c;可能会遇到一个常见的陷阱 - ​​循环变量捕获问题​​。让我详细解释一下&#xff1a; 问题背景 看这个代码片段&#xff1a; fo…...

编程新知 2026/1/21 14:29:57

使用分级同态加密防御梯度泄漏

抽象 联邦学习 &#xff08;FL&#xff09; 支持跨分布式客户端进行协作模型训练&#xff0c;而无需共享原始数据&#xff0c;这使其成为在互联和自动驾驶汽车 &#xff08;CAV&#xff09; 等领域保护隐私的机器学习的一种很有前途的方法。然而&#xff0c;最近的研究表明&…...

编程新知 2026/1/24 6:22:43

1688商品列表API与其他数据源的对接思路

将1688商品列表API与其他数据源对接时&#xff0c;需结合业务场景设计数据流转链路&#xff0c;重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点&#xff1a; 一、核心对接场景与目标 商品数据同步 场景&#xff1a;将1688商品信息…...

编程新知 2025/11/30 16:55:32

c++ 面试题(1)-----深度优先搜索（DFS）实现

操作系统&#xff1a;ubuntu22.04 IDE:Visual Studio Code 编程语言&#xff1a;C11 题目描述 地上有一个 m 行 n 列的方格&#xff0c;从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子&#xff0c;但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

编程新知 2026/1/10 10:16:16

【决胜公务员考试】求职OMG——见面课测验1

2025最新版&#xff01;&#xff01;&#xff01;6.8截至答题&#xff0c;大家注意呀&#xff01; 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:&#xff08; B &#xff09; A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

编程新知 2025/11/8 16:25:01

ABAP设计模式之---“简单设计原则(Simple Design)”

“Simple Design”&#xff08;简单设计&#xff09;是软件开发中的一个重要理念&#xff0c;倡导以最简单的方式实现软件功能&#xff0c;以确保代码清晰易懂、易维护&#xff0c;并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计&#xff0c;遵循“让事情保…...

编程新知 2026/1/27 18:13:23

七、数据库的完整性

七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

编程新知 2026/2/4 10:28:25

Ubuntu Cursor升级成v1.0

0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开&#xff0c;快捷键也不好用&#xff0c;当看到 Cursor 升级后&#xff0c;还是蛮高兴的 1. 下载 Cursor 下载地址&#xff1a;https://www.cursor.com/cn/downloads 点击下载 Linux (x64) &#xff0c;…...

编程新知 2026/2/4 16:04:11