备战蓝桥杯---贪心刷题1
话不多说,直接看题:

本质是一个数学题:

我们令xi<0表示反方向传递,易得我们就是求每一个xi的绝对值之和min,我们令平均值为a爸。
易得约束条件:
x1-x2=a1-a,x2-x3=a2-a.....
解得x1=x1-0,x2=x1-((n-1)*a-a2-...an)。。。。
这样就把问题转化成|x1-c1|+|x2-c2|+|...|....
又ci=ci+1+a-ai我们就可以吧c解出来,下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
const int N=1000010;
long long n,a[N];
long long sum=0;
long long c[N];
int main(){cin>>n;for(int i=1;i<=n;i++){scanf("%lld",&a[i]);sum+=a[i];}long long av=sum/n;for(int i=n;i>1;i--){c[i]=c[i+1]+av-a[i];}c[1]=0;sort(c+1,c+n+1);long long res=0;for(int i=1;i<=n;i++) res+=abs(c[i]-c[(i+1)/2]);cout<<res;
}接题:

先转换一下,我们从小岛的角度来看,看看每一个小岛可以被覆盖在x轴上对应的范围,这样问题就转换成了给定若干个区间,最少选多少个点可以使得每一个区间至少选了一个点。
如何贪心?我们先按照右端点排序,扫描每一个线段,若上一个右端点不在区间,那么选右端点。
若在则跳过。
如何严格证明?
我们记cnt为算法得到的结果,opt为最优解。
显然选了cnt个,那么就有cnt个互不相交的区间,因此答案一定大于等于cnt+opt是最优解,得证!
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
const int N=1010;
int n,d;
struct node{double l,r;
}seg[N];
bool cmp(node a,node b){return a.r<b.r;
}
int main(){cin>>n>>d;bool ff=0;for(int i=0;i<n;i++){int x,y;scanf("%d%d",&x,&y);if(y>d) ff=1;else{double ck=sqrt(d*d-y*y);seg[i].l=x-ck,seg[i].r=x+ck;}}if(ff) cout<<-1<<endl;else{sort(seg,seg+n,cmp);int cnt=0;double last=-1000000000;for(int i=0;i<n;i++){if(last<seg[i].l){cnt++;last=seg[i].r;}}cout<<cnt;}
}接题:

很容易想到,假如每一个人的钱都比平均大,那么都取平均即可。
假如有一个人少,那么让它填满,剩下的平均分摊给大于平均的。
下面是严格的证明:
我们把方差的每一项看成xi,xi的和为0,由均值不等式知我们要让每一个数尽可能相同,假如有一个小于平均值,假设它不选满,则结果肯定变大。
因此,若a1<平均值,那么我们就取a1,后面的式子满足加起来和为s-a1,因此剩下的加起来就是s-a1-(n-1)/n*s;此时每一个取到(s-a1)/(n-1)是最优的,而若此时大于该值,那么后面的肯定也大(排过序),因此取其即可。
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
const int N=500100;
int n,a[N];
int main(){long double s;scanf("%d%Lf",&n,&s);for(int i=0;i<n;i++) scanf("%d",&a[i]);sort(a,a+n);long double res=0,av=s/n;for(int i=0;i<n;i++){double cur=s/(n-i);if(a[i]<cur) cur=a[i];res+=(cur-av)*(cur-av);s-=cur;}printf("%.4Lf\n",sqrt(res/n));
}相关文章:

备战蓝桥杯---贪心刷题1
话不多说,直接看题: 本质是一个数学题: 我们令xi<0表示反方向传递,易得我们就是求每一个xi的绝对值之和min,我们令平均值为a爸。 易得约束条件: x1-x2a1-a,x2-x3a2-a..... 解得x1x1-0,x2x1-((n-1)*a-a2-...an)。…...
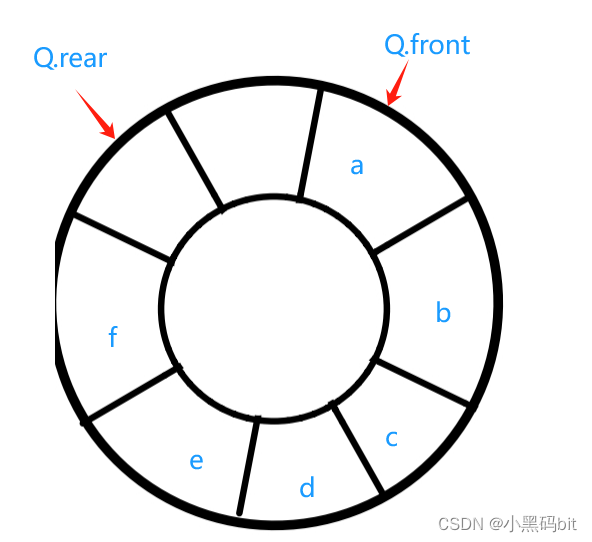
《数据结构学习笔记---第九篇》---循环队列的实现
文章目录 1.循环队列的定义 2.循环队列的判空判满 3.创建队列并初始化 4.入队和出队 5. 返回队尾队首元素 6.释放循环队列 1.循环队列的定义 定义:存储队列元素的表从逻辑上被视为一个环。 我们此次实现的循环队列,采用顺序表 typedef struct {int…...

前端调试工具之Chrome Elements、Network、Sources、TimeLine调试
常用的调试工具有Chrome浏览器的调试工具,火狐浏览器的Firebug插件调试工具,IE的开发人员工具等。它们的功能与使用方法大致相似。Chrome浏览器简洁快速,功能强大这里主要介绍Chrome浏览器的调试工具。 打开 Google Chrome 浏览器,…...
vue 加 websocket 聊天
<template><div style="height: 100%; width: 100%; background-color: #fff"><div class="wrap"><!-- 头部 --><div class="titleBox"><imgsrc="@/assets/image/avatar.png"style="argin: 10p…...
)
uniapp通过蓝牙传输数据 (ios)
在uni-app中,可以通过uni-ble(uni-app官方提供的蓝牙插件)来实现iOS设备上的蓝牙数据传输。 首先,确保已在uni-app的manifest.json文件中添加uni-ble插件的配置: "permission": { "scope.userLocati…...
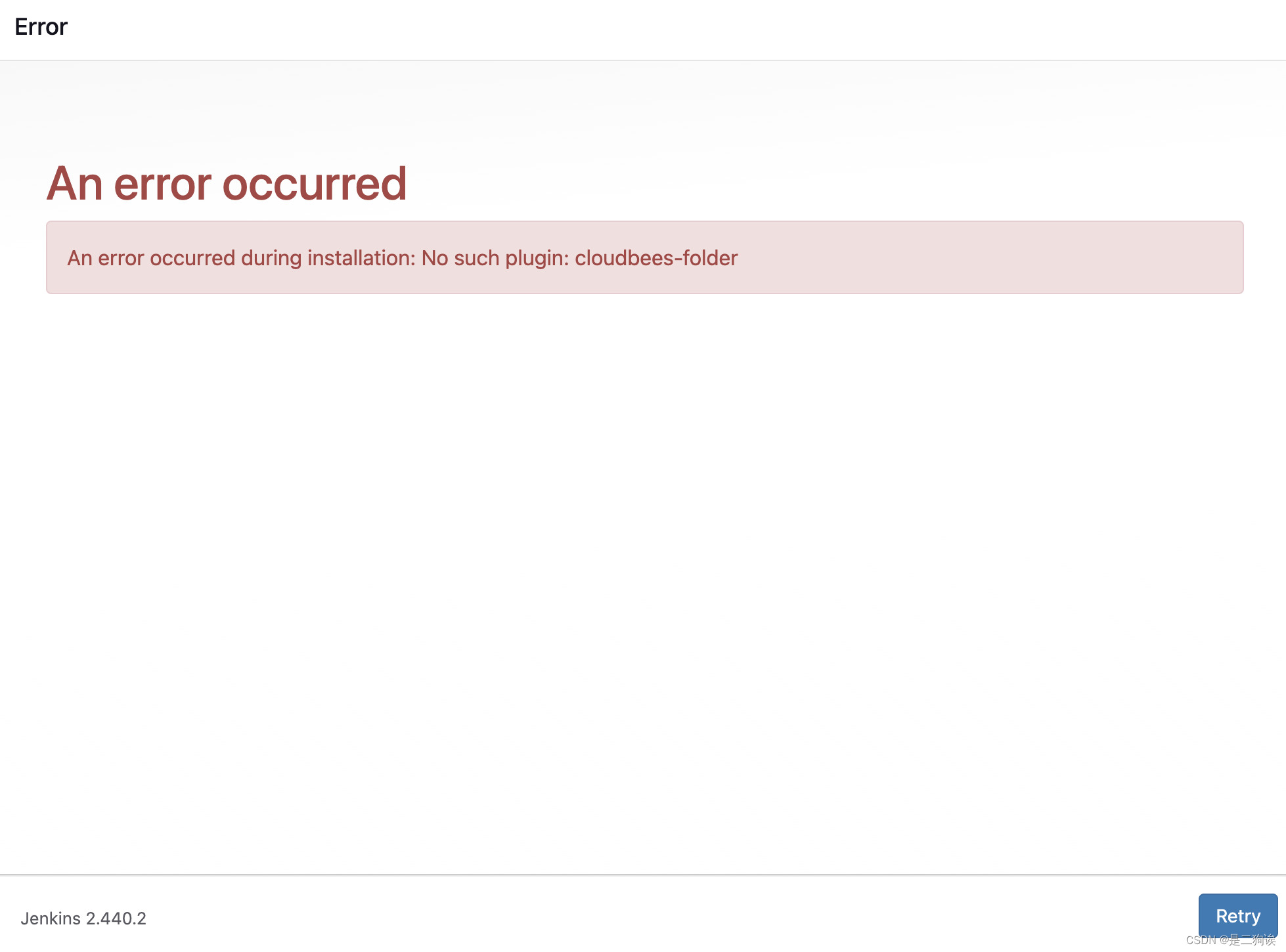
docker搭建CI/CD环境配置过程中的常见问题
一、Jenkins 1、pull镜像问题 docker pull jenkins/jenkins:lts Using default tag: latest Trying to pull repository docker.io/library/centos ... Get https://registry-1.docker.io/v2/library/centos/manifests/latest: Get https://auth.docker.io/token?scoperepo…...
实验四 微信小程序智能手机互联网程序设计(微信程序方向)实验报告
请编写一个用户登录界面,提示输入用户名和密码进行登录; 代码 index.wxml <view class"user"> <form bindreset""> <view>用户名:</view><input type"text"name""/>…...

WPF —— 关键帧动画
wpf动画类型 1<类型>Animation这些动画称为from/to/by动画或者叫基本动画,他们会在起始值或者结束值进行动画处理,常用的例如 <DoubleAnimation> 2 <类型>AnimationUsingKeyFrames: 关键帧动画,功能要比from/to这些动画功…...
Taro + vue3 小程序封装标题组件
分为没有跳转页面的title组件和 有跳转页面的title组件 我们可以把这个封装成一个组件 直接上代码 <template><div class"fixed-title-container"><div class"box"><div class"icon" v-if"isShow" click"…...
-babyCoder源码阅读2任务描述部分)
babyAGI(6)-babyCoder源码阅读2任务描述部分
废话不多说,我们直接看task的prompt 这里需要注意的是,每个openai_call的temperature都不相同,这也是开发程序时需要调整和关注的一点 1. 初始化代码任务agent 作为babycoder的第一个angent,整个prompt编写的十分值得学习 整个p…...

生成式语言模型预训练阶段验证方式与微调阶段验证方式
生成式语言模型,如GPT-3、BERT等,在预训练和微调阶段都需要进行验证以确保模型性能。下面分别介绍这两个阶段的验证方式: 预训练阶段的验证: 预训练阶段通常使用大量未标注的文本数据来训练模型,以学习语言的一般特性。…...
flink on yarn
前言 Apache Flink,作为大数据处理领域的璀璨明星,以其独特的流处理和批处理一体化模型,成为众多企业和开发者的首选。它不仅能够在处理无界数据流时展现出卓越的实时性能,还能在有界数据批处理上达到高效稳定的效果。本文将简要…...

用TOMCAT部署web项目教程
文章目录 引言I 使用webapps文件夹II 利用server.xmlIII 自定义配置文件IV 预备知识4.1项目的一般结构4.2 contex标签4.3 IDE部署4.4 配置Tomcat服务引言 在开发阶段,一般使用IDE如MyEclipse来部署web项目,不要忘记手动部署的三种方式。 I 使用webapps文件夹 将项目文件夹…...

bash例子-source进程替换、alias不生效处理
#1. source 例子, 进程替换source <(echo alias zls"ls") #上一行 中 echo替换为cat,则得到如下行, 好处是 cat不用处理引号转义问题,而echo则必须处理引号转义问题#写一段复杂脚本,且 不处理引号转义问题 &#x…...
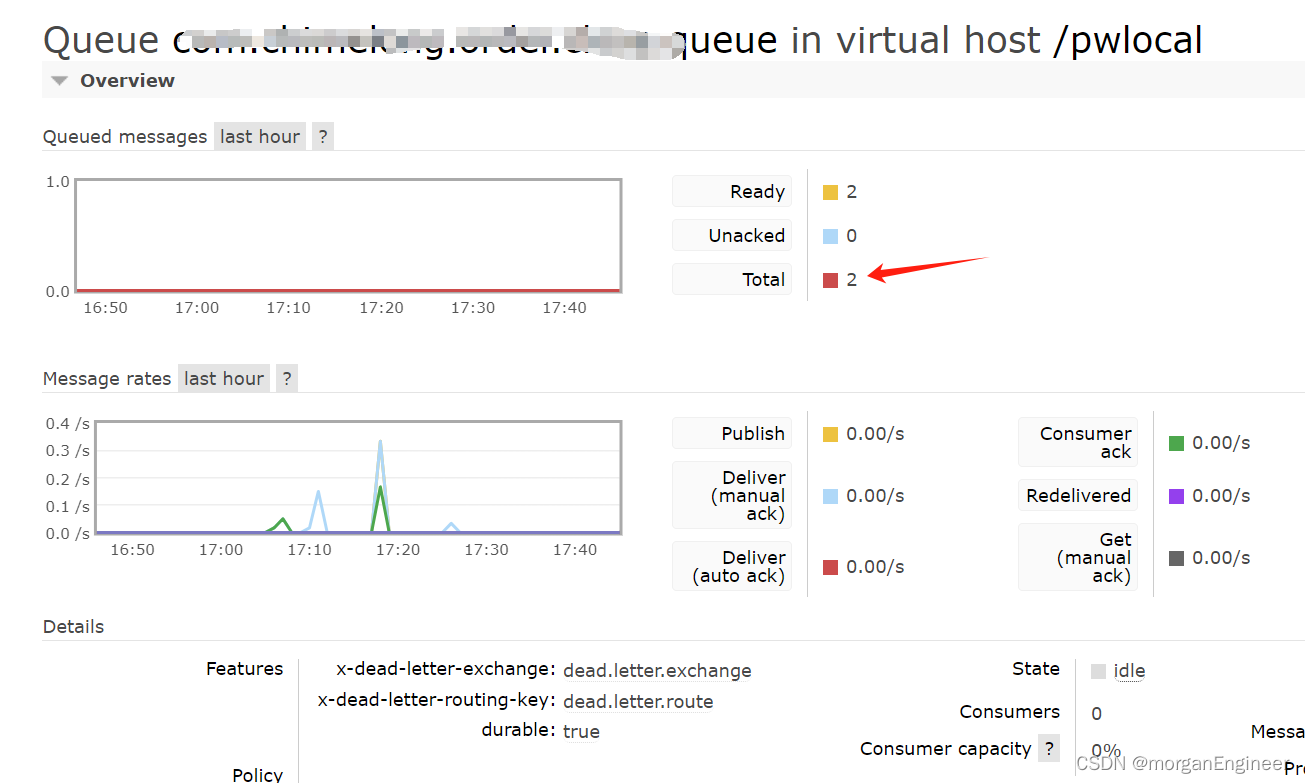
rabbitmq死信交换机,死信队列使用
背景 对于核心业务需要保证消息必须正常消费,就必须考虑消费失败的场景,rabbitmq提供了以下三种消费失败处理机制 直接reject,丢弃消息(默认)返回nack,消息重新入队列将失败消息投递到指定的交换机 对于核…...

gitlab备份与恢复
1.1.1 查看系统版本和软件版本 cat /etc/debian_version cat /opt/gitlab/embedded/service/gitlab-rails/VERSION 1.1.2 数据备份 打开/etc/gitlab/gitlab.rb配置文件,查看一个和备份相关的配置项 sudo vim /etc/gitlab/gitlab.rb gitlab_rails[backup_path] &q…...
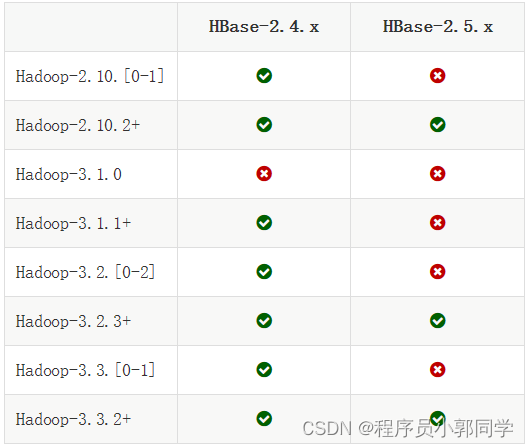
HBase详解(1)
HBase 简介 概述 HBase是Yahoo!公司开发的后来贡献给了Apache的一套开源的、分布式的、可扩展的、基于Hadoop的非关系型数据库(Non-Relational Database),因此HBase并不支持SQL(几乎所有的非关系型数据库都不支持SQL),而是提供了一套单独的命令和API操…...

深入理解数据结构第二弹——二叉树(2)——堆排序及其时间复杂度
看这篇前请先把我上一篇了解一下:深入理解数据结构第一弹——二叉树(1)——堆-CSDN博客 前言: 相信很多学习数据结构的人,都会遇到一种情况,就是明明最一开始学习就学习了时间复杂度,但是在后期…...

视频汇聚/安防监控/EasyCVR平台播放器EasyPlayer更新:新增【性能面板】
视频汇聚/安防监控/视频存储平台EasyCVR基于云边端架构,可以在复杂的网络环境中快速、灵活部署,平台视频能力丰富,可以提供实时远程视频监控、视频录像、录像回放与存储、告警、语音对讲、云台控制、平台级联、磁盘阵列存储、视频集中存储、云…...

【教程】Flutter 应用混淆
在移动应用开发中,保护应用代码安全至关重要。Flutter 提供了简单易用的混淆工具,帮助开发者在构建 release 版本应用时有效保护代码。本文将介绍如何在 Flutter 应用中使用混淆,并提供了相关的操作步骤和注意事项。 📝 摘要 本…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...
