牛客2024年愚人节比赛(A-K)
比赛链接
毕竟是娱乐场,放平心态打吧。。。
只有A一个考了数学期望,其他的基本都是acmer特有的脑筋急转弯,看个乐呵即可。
A 我是欧皇,赚到盆满钵满!
思路:
我们有 p 1 p_1 p1 的概率直接拿到一件实物,有 1 − p 1 1-p_1 1−p1 的概率拿到 10 10 10 牛币,然后去第二个抽奖。第二个是 p 2 p_2 p2 的概率拿到一件实物, p 3 p_3 p3 的概率重新抽卡, 剩下的概率就啥也没有。另外的第三四个抽奖和前面没有关系,第三个抽到实物的概率是 p 4 p_4 p4,第四个是 1 10 \dfrac1{10} 101。
我们假设第二个抽奖拿到实物的期望为 f f f,那么有: f = p 2 ∗ 1 + p 3 ∗ f f=p_2*1+p_3*f f=p2∗1+p3∗f ( 1 − p 3 ) ∗ f = p 2 (1-p_3)*f=p_2 (1−p3)∗f=p2 f = p 2 1 − p 3 f=\dfrac{p_2}{1-p_3} f=1−p3p2我们有 1 − p 1 1-p_1 1−p1 能拿到牛币,才能去第二个抽奖,这样第一个抽奖拿到实物的期望就是 p 1 ∗ 1 + ( 1 − p 1 ) ∗ f p_1*1+(1-p_1)*f p1∗1+(1−p1)∗f p 1 + ( 1 − p 1 ) ∗ p 2 1 − p 3 p_1+\dfrac{(1-p_1)*p_2}{1-p_3} p1+1−p3(1−p1)∗p2
那么总的拿到实物的期望就是 p 1 + ( 1 − p 1 ) ∗ p 2 1 − p 3 + p 4 + 1 10 p_1+\dfrac{(1-p_1)*p_2}{1-p_3}+p_4+\dfrac1{10} p1+1−p3(1−p1)∗p2+p4+101
code:
#include <iostream>
#include <cstdio>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;ll qpow(ll a,ll b){b%=mod-1;ll base=a%mod,ans=1;while(b){if(b&1){ans=(base*ans)%mod;}base=(base*base)%mod;b>>=1;}return ans;
}ll inv(ll x){return qpow(x,mod-2);}ll a,b,c,d,e,f,g,h;
ll p1,p2,p3,p4;int main(){cin>>a>>b>>c>>d>>e>>f>>g>>h;p1=a*inv(b)%mod;p2=c*inv(d)%mod;p3=e*inv(f)%mod;p4=g*inv(h)%mod;cout<<(p1+p2*(1-p1+mod)%mod*inv(1-p3+mod)%mod+p4+inv(10))%mod;return 0;
}
B 我是欧皇,赚到盆满钵满!(fool version)
思路:
不难,也没啥坑,但是榜歪了没人写。
第一三四个抽奖只能玩一次,只能拿到有限的实物,所以我们可以直接无视。因为我们有无限的牛币,可以抽无限次,所以只要第二个抽奖有概率能拿到实物,那么就相当于可以拿到无限的实物。因此这个题只要保证 p 2 > 0 p_2>0 p2>0 就行了。
code:
#include <iostream>
#include <cstdio>
using namespace std;
typedef long long ll;ll a,b,c,d,e,f,g,h;int main(){cin>>a>>b>>c>>d>>e>>f>>g>>h;if(c!=0)cout<<"Infinity";else cout<<"limited";return 0;
}
C 征战沙场
思路:
不懂出题人的脑回路。
样例说明说没有队友,所以你不属于任何一方。最少要和打剩下的人打,最多要全打一遍。
code:
#include <iostream>
#include <cstdio>
using namespace std;int x,y;int main(){cin>>x>>y;cout<<abs(x-y)<<" "<<x+y;return 0;
}
D 炼药锅
思路:
经典脑筋急转弯。
这题不是问你有几口锅,而是锅有几个口。
code:
#include <iostream>
#include <cstdio>
using namespace std;int main(){cout<<1;return 0;
}
E what connection?
思路:
参考牛客题解讨论区。
这几个单词是 .io .edu .cn .one .com .org 等域名的全称。它们都是 顶级域名(top-level domain)
code:
#include <iostream>
#include <cstdio>
using namespace std;int main(){cout<<"top-level domain";return 0;
}
F 逻辑大师
思路:
数学天才,逻辑大师可以手玩。我是逻辑低手,我选择爆搜。
code:
没写,愚人节满课,清明还要调休,题面看着就来气。尝试当逻辑糕手的时候还推错了(以为第三题正确答案以外的其他三个选项的答案是一致的)。
答案如下:
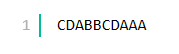
G mutsumi的……&数#¥@数
思路:
随便搜个乱码恢复的网站丢上去大概能得到这个:

mutumi有一个数组,她想知道数组里正数和负数共有几个
彩蛋我是真没找到
code:
#include <iostream>
#include <cstdio>
using namespace std;int n,ans;int main(){cin>>n;for(int i=1,t;i<=n;i++){cin>>t;if(t!=0)ans++;}cout<<ans<<endl;return 0;
}
H 一个简单的数学题
思路:
1e18是个浮点数,因此有可能会出现精度损失。在一个大浮点数和小浮点数相加的时候,小数可能直接舍入导致消失了。
code:
#include <iostream>
#include <cstdio>
using namespace std;int main(){int i;for(i=1;1e18+i==1e18;i++);cout<<i-1;return 0;
}
I 小苯的排列构造
思路:
从 1 1 1 按顺序输出到 n n n 即可。因为相邻两数一定是互质的。
证明可以利用辗转相除法。众所周知 g c d ( a , b ) = g c d ( b , a % b ) gcd(a,b)=gcd(b,a\%b) gcd(a,b)=gcd(b,a%b),当 a = b + 1 a=b+1 a=b+1(两数相邻)时,就有 g c d ( a , b ) = g c d ( b + 1 , b ) = g c d ( b , 1 ) = 1 gcd(a,b)=gcd(b+1,b)=gcd(b,1)=1 gcd(a,b)=gcd(b+1,b)=gcd(b,1)=1
code:
#include <iostream>
#include <cstdio>
using namespace std;int T,n;int main(){cin>>T;while(T--){cin>>n;for(int i=1;i<=n;i++)cout<<i<<" \n"[i==n];}return 0;
}
J ✌
思路:
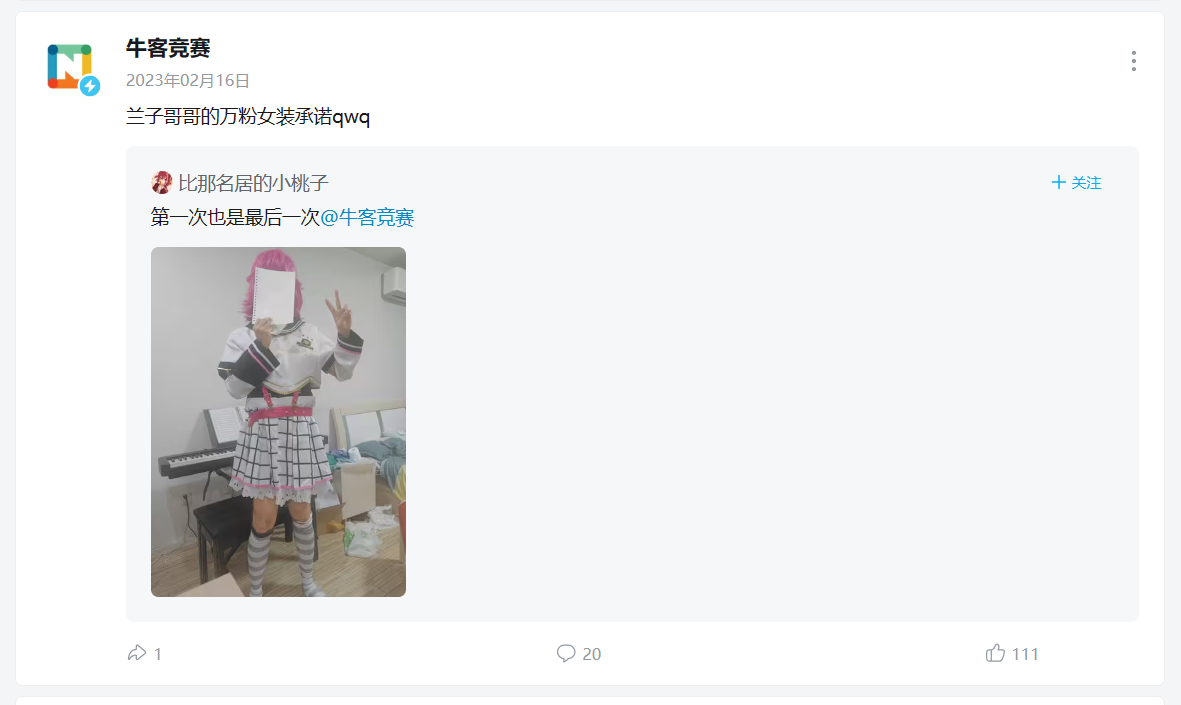
https://t.bilibili.com/762931495002177560
都给我去看兰子哥哥的女装!
网址中很容易看出来和bilibili有关,还要和牛客有关,从牛客B站官方动态一路往下翻就翻到了。
code:
#include <iostream>
#include <cstdio>
using namespace std;int main(){cout<<"https://t.bilibili.com/762931495002177560";return 0;
}
K white-collar teacher 说唱歌手 me
思路:
看评论区题解:
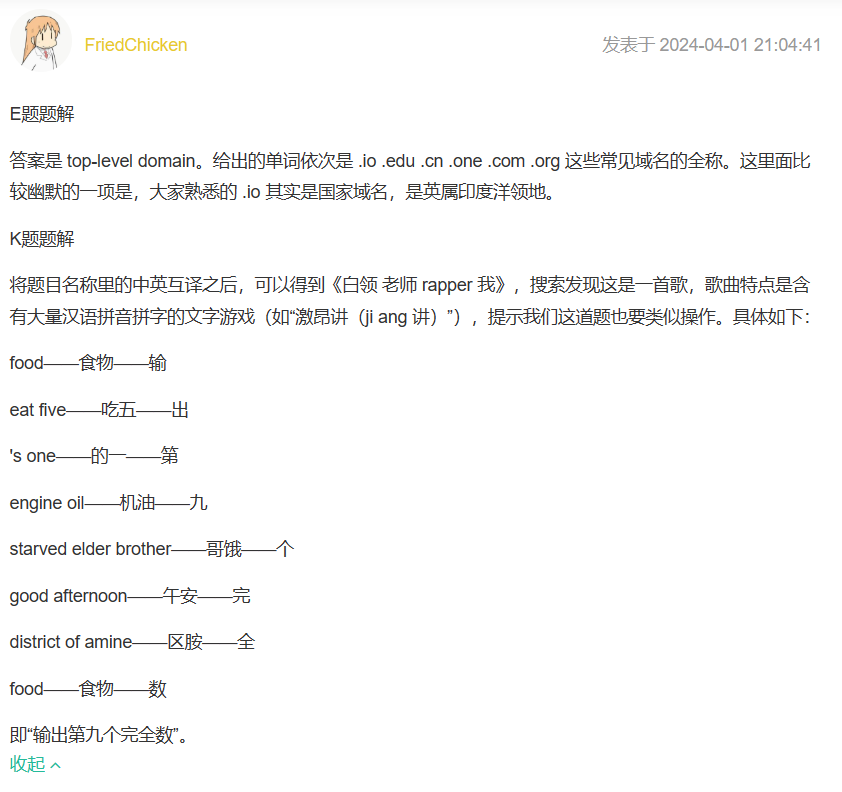
完全数的定义:

直接搜可以得到第九个完全数。
6,28,496,8128,33550336,8589869056,137438691328,2305843008139952128,2658455991569831744654692615953842176,191561942608236107294793378084303638130997321548169216,13164036458569648337239753460458722910223472318386943117783728128,14474011154664524427946373126085988481573677491474835889066354349131199152128
code:
#include <iostream>
#include <cstdio>
using namespace std;int main(){cout<<"2658455991569831744654692615953842176"<<endl;return 0;
}
相关文章:

牛客2024年愚人节比赛(A-K)
比赛链接 毕竟是娱乐场,放平心态打吧。。。 只有A一个考了数学期望,其他的基本都是acmer特有的脑筋急转弯,看个乐呵即可。 A 我是欧皇,赚到盆满钵满! 思路: 我们有 p 1 p_1 p1 的概率直接拿到一件实…...

loadbalancer 引入与使用
在消费中pom中引入 <dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-starter-loadbalancer</artifactId> </dependency> 请求调用加 LoadBalanced 注解 进行服务调用 默认负载均衡是轮训模式 想要切换…...

Yolov5封装detect.py面向对象
主要目标是适应摄像头rtsp流的检测 如果是普通文件夹或者图片,run中的while True去掉即可。 web_client是根据需求创建的客户端,将检测到的数据打包发送给服务器 # YOLOv5 🚀 by Ultralytics, GPL-3.0 license """ Run inf…...

入门级深度学习主机组装过程
一 配置 先附上电脑配置图,如下: 利用公司的办公电脑对配置进行升级改造完成。除了显卡和电源,其他硬件都是公司电脑原装。 二 显卡 有钱直接上 RTX4090,也不能复用公司的电脑,其他配置跟不上。 进行深度学习&…...
python爬虫之selenium4使用(万字讲解)
文章目录 一、前言二、selenium的介绍1、优点:2、缺点: 三、selenium环境搭建1、安装python模块2、selenium4新特性3、安装驱动WebDriver驱动选择驱动安装和测试 基础操作1、属性和方法2、单个元素定位通过id定位通过class_name定位一个元素通过xpath定位…...

【ARM 嵌入式 C 头文件系列 22 -- 头文件 stdint.h 介绍】
请阅读【嵌入式开发学习必备专栏 】 文章目录 C 头文件 stdint.h定长整数类型最小宽度整数类型最快最小宽度整数类型整数指针类型最大整数类型 C 头文件 stdint.h 在 C 语言中,头文件 <stdint.h> 是 C99 标准的一部分,旨在提供一组明确的整数类型…...
LabVIEW专栏三、探针和断点
探针和断点是LabVIEW调试的常用手段,该节以上一节的"测试耗时"为例 探针可以打在有线条的任何地方,打上后,经过这条线的所有最后一次的数值都会显示在探针窗口。断点可以打在程序框图的所有G代码对象,包括结构…...
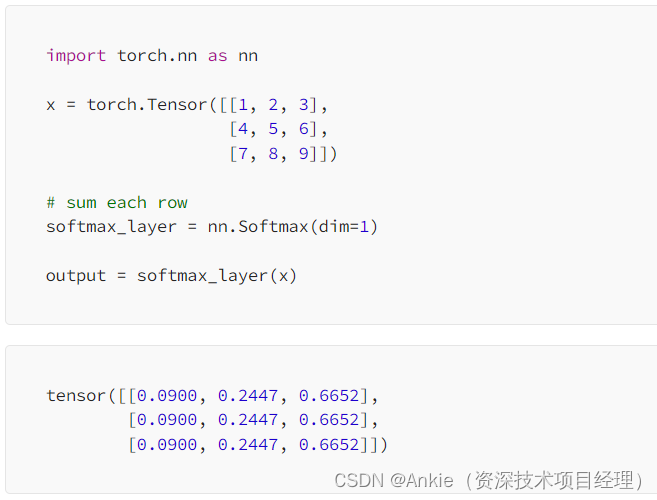
Transformer模型-softmax的简明介绍
今天介绍transformer模型的softmax softmax的定义和目的: softmax:常用于神经网络的输出层,以将原始的输出值转化为概率分布,从而使得每个类别的概率值在0到1之间,并且所有类别的概率之和为1。这使得Softmax函数特别适…...

记录一下做工厂的打印pdf程序
功能:在网页点击按钮调起本地的打印程序 本人想到的就是直接调起方式,网上大佬们说用注册表的形式来进行。 后面想到一种,在电脑开机时就开启,并在后台运行,等到有人去网页里面进行触发,这时候就有个问题&a…...
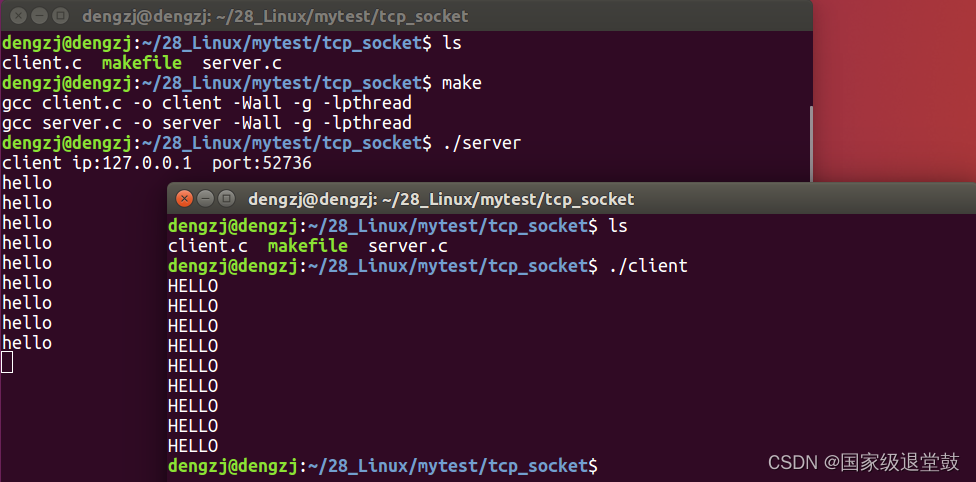
Linux网络编程一(协议、TCP协议、UDP、socket编程、TCP服务器端及客户端)
文章目录 协议1、分层模型结构2、网络应用程序设计模式3、ARP协议4、IP协议5、UDP协议6、TCP协议 Socket编程1、网络套接字(socket)2、网络字节序3、IP地址转换4、一系列函数5、TCP通信流程分析 第二次更新,自己再重新梳理一遍… 协议 协议:指一组规则&…...
Python读取Excel根据每行信息生成一个PDF——并自定义添加文本,可用于制作准考证
文章目录 有点小bug的:最终代码(无换行):有换行最终代码无bug根据Excel自动生成PDF,目录结构如上 有点小bug的: # coding=utf-8 import pandas as pd from reportlab.pdfgen import canvas from reportlab.lib.pagesizes import letter from reportlab.pdfbase import pdf…...

http: server gave HTTP response to HTTPS client 分析一下这个问题如何解决中文告诉我详细的解决方案
这个错误信息表明 Docker 客户端在尝试通过 HTTPS 协议连接到 Docker 仓库时,但是服务器却返回了一个 HTTP 响应。这通常意味着 Docker 仓库没有正确配置为使用 HTTPS,或者客户端没有正确配置以信任仓库的 SSL 证书。以下是几种可能的解决方案࿱…...
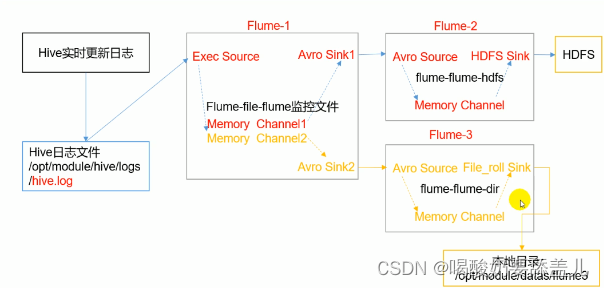
Flume学习笔记
视频地址:https://www.bilibili.com/video/BV1wf4y1G7EQ/ 定义 Flume是一个高可用的、高可靠的、分布式的海量日志采集、聚合和传输的系统。 Flume高最要的作用就是实时读取服务器本地磁盘的数据,将数据写入HDFS。 官网:https://flume.apache.org/releases/content/1.9.0/…...
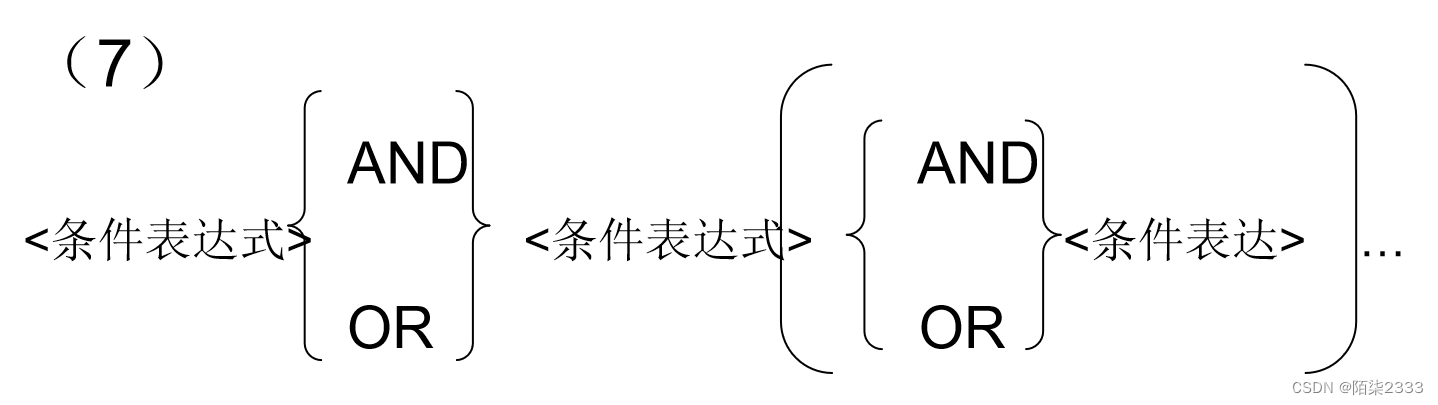
数据库系统概论(超详解!!!) 第三节 关系数据库标准语言SQL(Ⅳ)
1.集合查询 集合操作的种类 并操作UNION 交操作INTERSECT 差操作EXCEPT 参加集合操作的各查询结果的列数必须相同;对应项的数据类型也必须相同 查询计算机科学系的学生及年龄不大于19岁的学生。SELECT *FROM StudentWHERE Sdept CSUNIONSELECT *FROM StudentWHERE Sage&l…...

与谷歌“分家”两年后,SandboxAQ推出统一加密管理平台
3月27日,SandboxAQ宣布其AQtive Guard平台现已全面可用(GA),适用于所有行业,以防范人工智能驱动和量子攻击的威胁。前者是在两年前3月从谷歌母公司Alphabet分拆出来的初创公司,并在当时获得了“九位数”的融…...
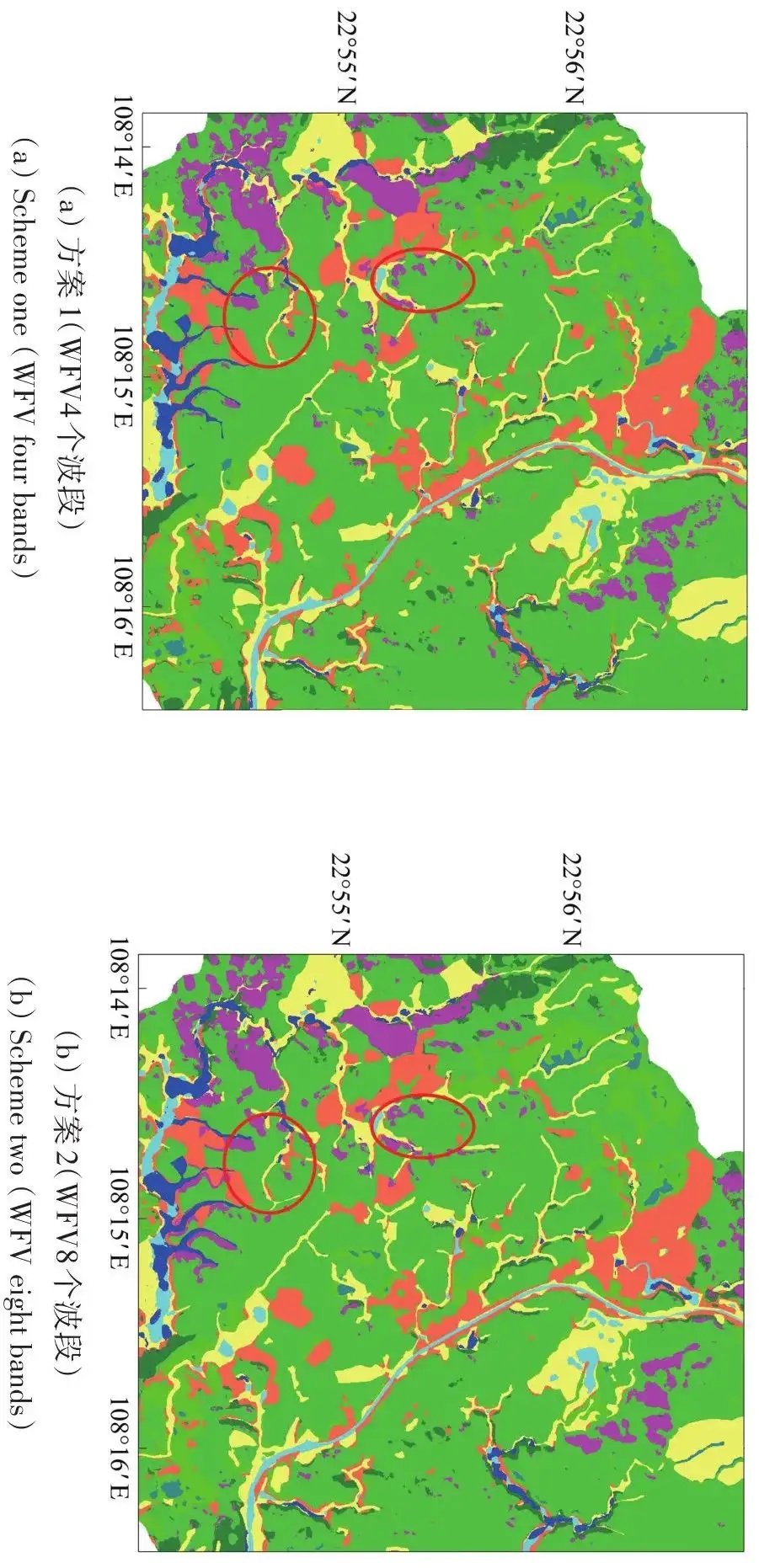
【卫星家族】 | 高分六号卫星影像及获取
1. 卫星简介 高分六号卫星(GF-6)于2018年6月2日在酒泉卫星发射中心成功发射,是高分专项中的一颗低轨光学遥感卫星,也是我国首颗精准农业观测的高分卫星,具有高分辨率、宽覆盖、高质量成像、高效能成像、国产化率高等特…...

XML与Xpath
XML与Xpath XML是一种具有某种层次结构的文件,Xpath则是解析这种文件的工具 接下来将会解释XML文件的结构和Xpath的基本使用,并且用Java语言进行操作展示。 XML结构 XML(可扩展标记语言)文件具有一种层次结构,由标签…...

【c++20】CPP-20-STL-Cookbook 学习笔记
Cpp20-STL-Cookbook-src简单的阅读笔记。c++20更好用了,比如STL 包含了一些这样的辅助函数,比如 make_pair() 和make_tuple() 等。 这些代码现在已经过时了,但是为了与旧代码兼容,会保留这些代码。比如 可以声明是一个std的string:Sum s1 {1u, 2.0, 3, 4.0f }?...

Python 之 Flask 框架学习
毕业那会使用过这个轻量级的框架,最近再来回看一下,依赖相关的就不多说了,直接从例子开始。下面示例中的 html 模板,千万记得要放到 templates 目录下。 Flask基础示例 hello world from flask import Flask, jsonify, url_fora…...
精品丨PowerBI负载测试和容量规划
当选择Power BI作为业务报表平台时,如何判断许可证的选择是否符合业务需求,价格占了主导因素。 Power BI的定价是基于SKU和服务器内核决定的,但是很多IT的负责人都不确定自己公司业务具体需要多少。 不幸的是,Power BI的容量和预期…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...
