AcWing - 蓝桥杯集训每日一题(DAY 1——DAY 5)
文章目录
- 一、AcWing 3956. 截断数组(中等)
- 1. 实现思路
- 2. 实现代码
- 二、AcWing 3729. 改变数组元素(中等)
- 1. 实现思路
- 2. 实现代码
- 三、AcWing 1460. 我在哪?(简单)
- 1. 实现思路
- 2. 实现代码
- 四、AcWing 3768. 字符串删减(简单)
- 1. 实现思路
- 2. 实现代码
- 五、AcWing 3777. 砖块(简单)
- 1. 实现思路
- 2. 实现代码
一、AcWing 3956. 截断数组(中等)
题目描述
给定一个长度为 nnn 的数组 a1,a2,…,ana_{1},a_{2},…,a_{n}a1,a2,…,an。
现在,要将该数组从中间截断,得到三个非空子数组。
要求,三个子数组内各元素之和都相等。
请问,共有多少种不同的截断方法?
输入格式
第一行包含整数 nnn。
第二行包含 nnn 个整数 a1,a2,…,ana_{1},a_{2},…,a_{n}a1,a2,…,an。
输出格式
输出一个整数,表示截断方法数量。
数据范围
前六个测试点满足: 1≤n≤101≤n≤101≤n≤10。
所有测试点满足: 1≤n≤105,−10000≤ai≤100001≤n≤10^{5},−10000≤a_{i}≤100001≤n≤105,−10000≤ai≤10000。
输入样例 1
4
1 2 3 3
输出样例 1
1
输入样例 2
5
1 2 3 4 5
输出样例 2
0
输入样例 3
2
0 0
输出样例 3
0
具体实现
1. 实现思路
- 我们有一个长度为 n 的数组,将其分成三段,使三段内的元素都相等,求有多少种截断方法。
- 首先,我们可以先求解一些总和 s,如果 3 不可以整除总和 s 的话,就一定无解。如果想要有解的话,s 一定是 3 的倍数。因此,我们可以先计算出总和 s 和每一段的总和 s/3。
- 问题就转变为一共有多少种选法,使得每一段的和都是 s/3。
- 我们可以先确定后面的点,让前面的总和是 2s/3,再选择前面的点,满足第一段是 s/3。
- 我们再枚举的过程中,可以使用前缀和,计算出从起始点到每一段的前缀和,判断第一段前缀和是 s/3,第二段前缀和是 2s/3 即可。
2. 实现代码
#include <bits/stdc++.h>
using namespace std;
int n;
int a[100005];
long long res=0,cnt=0;
int main()
{cin>>n;for(int i=1;i<=n;i++){int x=0;cin>>x;a[i]=a[i-1]+x; //前缀和数组}if(a[n]%3!=0 || n<3){cout<<"0"<<endl;}else{for(int j=2;j<n;j++){if(a[j-1]==a[n]/3){cnt++;}if(a[j]==a[n]/3*2){res+=cnt;}}cout<<res;}return 0;
}
二、AcWing 3729. 改变数组元素(中等)
题目描述
给定一个空数组 VVV 和一个整数数组 a1,a2,…,ana_{1},a_{2},…,a_{n}a1,a2,…,an。
现在要对数组 VVV 进行 nnn 次操作。
第 iii 次操作的具体流程如下:
- 从数组 VVV 尾部插入整数 000。
- 将位于数组 VVV 末尾的 aia_{i}ai 个元素都变为 111(已经是 111 的不予理会)。
注意:
- aia_{i}ai 可能为 0,即不做任何改变。
- aia_{i}ai 可能大于目前数组 V 所包含的元素个数,此时视为将数组内所有元素变为 111。
请你输出所有操作完成后的数组 VVV。
输入格式
第一行包含整数 TTT,表示共有 TTT 组测试数据。
每组数据第一行包含整数 nnn。
第二行包含 nnn 个整数 a1,a2,…,ana_{1},a_{2},…,a_{n}a1,a2,…,an。
输出格式
每组数据输出一行结果,表示所有操作完成后的数组 VVV,数组内元素之间用空格隔开。
数据范围
1≤T≤200001≤T≤200001≤T≤20000
1≤n≤2×1051≤n≤2×10^{5}1≤n≤2×105
0≤ai≤n0≤a_{i}≤n0≤ai≤n
保证一个测试点内所有 nnn 的和不超过 2×1052×10^{5}2×105。
输入样例
3
6
0 3 0 0 1 3
10
0 0 0 1 0 5 0 0 0 2
3
0 0 0
输出样例
1 1 0 1 1 1
0 1 1 1 1 1 0 0 1 1
0 0 0
具体实现
1. 实现思路
- 由于我们每次操作都会加入一个数,在操作 i 次之后,新数组的长度就是 i,然后,再将当前数组的最后面的 ai 个数变成 1。
- 由于第 i 次数组一共有 i 个,将后 ai 个数变为 1,也就是我们将是 i-ai+1 到 i 的区间内的 ai 个数全部变成 1,也就是这个区间内的数据操作一次。
- 因此,我们可以开一个新数组与原数组长度相等,用以记录区间内数据操作的个数,因为 V 数组当中的 1 不会发生改变,所以,操作多次和操作一次的效果是相同的。
- 最后,如果新数组当中的元素大于 0,那么 V 数组中对应的元素就是 1,如果新数组中的元素等于 0,那么 V 数组中对应的元素就是 0。
2. 实现代码
#include <bits/stdc++.h>
using namespace std;
const int N=200010;
int n;
int b[N];
int main()
{int T;cin>>T;while(T--){cin>>n;memset(b,0,(n+1)*4);for(int i=1;i<=n;i++){int x;cin>>x;x=min(x,i); //如果x大于i的话就更新成i,因为此时是将数组内的所有元素变为1 int l=i-x+1,r=i; b[l]++;b[r+1]--;}for(int i=1;i<=n;i++){b[i]+=b[i-1];}for(int i=1;i<=n;i++){cout<<!!b[i]<<" ";}cout<<endl;}return 0;
}
三、AcWing 1460. 我在哪?(简单)
题目描述
农夫约翰出门沿着马路散步,但是他现在发现自己可能迷路了!
沿路有一排共 NNN 个农场。
不幸的是农场并没有编号,这使得约翰难以分辨他在这条路上所处的位置。
然而,每个农场都沿路设有一个彩色的邮箱,所以约翰希望能够通过查看最近的几个邮箱的颜色来唯一确定他所在的位置。
每个邮箱的颜色用 A..ZA..ZA..Z 之间的一个字母来指定,所以沿着道路的 NNN 个邮箱的序列可以用一个长为 NNN 的由字母 A..ZA..ZA..Z 组成的字符串来表示。
某些邮箱可能会有相同的颜色。
约翰想要知道最小的 KKK 的值,使得他查看任意连续 KKK 个邮箱序列,他都可以唯一确定这一序列在道路上的位置。
例如,假设沿路的邮箱序列为 ABCDABC 。
约翰不能令 K=3K=3K=3,因为如果他看到了 ABC,则沿路有两个这一连续颜色序列可能所在的位置。
最小可行的 KKK 的值为 K=4K=4K=4,因为如果他查看任意连续 444 个邮箱,那么可得到的连续颜色序列可以唯一确定他在道路上的位置。
输入格式
输入的第一行包含 NNN,第二行包含一个由 NNN 个字符组成的字符串,每个字符均在 A..ZA..ZA..Z 之内。
输出格式
输出一行,包含一个整数,为可以解决农夫约翰的问题的最小 KKK 值。
数据范围
1≤N≤1001≤N≤1001≤N≤100
输入样例
7
ABCDABC
输出样例
4
具体实现
1. 实现思路
- 我们要找到一个最小的 K,使得字符串当中从 K 分开不存在两个相同的字符串。
- 我们可以使用暴力解法,也就是 4 个 for 循环,第一重循环枚举每一个 K,第二重循环枚举第一个子串,第三重循环枚举第二个子串,第四重循环判断两个字串是否相同。
2. 实现代码
#include <bits/stdc++.h>
using namespace std;
int n;
string str;
int main()
{cin >> n >> str;for (int k = 1; k <= n; k ++ ){bool flag = false;for (int i = 0; i + k - 1 < n; i ++ ){for (int j = i + 1; j + k - 1 < n; j ++ ){bool same = true;for (int u = 0; u < k; u ++ )if (str[i + u] != str[j + u]){same = false;break;}if (same){flag = true;break;}}if (flag) break;}if (!flag){cout << k << endl;break;}}return 0;
}
四、AcWing 3768. 字符串删减(简单)
题目描述
给定一个由 nnn 个小写字母构成的字符串。
现在,需要删掉其中的一些字母,使得字符串中不存在连续三个或三个以上的 xxx。
请问,最少需要删掉多少个字母?
如果字符串本来就不存在连续的三个或三个以上 xxx,则无需删掉任何字母。
输入格式
第一行包含整数 nnn。
第二行包含一个长度为 nnn 的由小写字母构成的字符串。
输出格式
输出最少需要删掉的字母个数。
数据范围
3≤n≤1003≤n≤1003≤n≤100
输入样例 1
6
xxxiii
输出样例 1
1
输入样例 2
5
xxoxx
输出样例 2
0
输入样例 3
10
xxxxxxxxxx
输出样例 3
8
具体实现
1. 实现思路
- 我们利用 cnt 存储当前连续出现字符 x 的个数。
- 若出现了一个字符 x,则 cnt 加一。
- 若出现了一个其它字符,则 cnt 清零。
- 若当前 cnt=3,说明遇到了连续三个 x,此时需要删除一次。特别地,此时删除最后一个字符 x 后,可能补位的字符仍为 x,如输入样例 3 所示。此时不能将 cnt 清零,而应该减一,然后继续遍历。
2. 实现代码
#include <bits/stdc++.h>
using namespace std;int main()
{int n;string s;cin>>n>>s;int res=0,cnt=0;for(int i=0;i<n;i++){if(s[i]=='x'){cnt++;if(cnt==3){cnt--;res++;}}else{cnt=0;}}cout<<res<<endl;return 0;
}五、AcWing 3777. 砖块(简单)
题目描述
nnn 个砖块排成一排,从左到右编号依次为 1∼n1∼n1∼n。
每个砖块要么是黑色的,要么是白色的。
现在你可以进行以下操作若干次(可以是 000 次):
选择两个相邻的砖块,反转它们的颜色。(黑变白,白变黑)
你的目标是通过不超过 3n3n3n 次操作,将所有砖块的颜色变得一致。
输入格式
第一行包含整数 TTT,表示共有 TTT 组测试数据。
每组数据第一行包含一个整数 nnn。
第二行包含一个长度为 nnn 的字符串 sss。其中的每个字符都是 W 或 B,如果第 iii 个字符是 W,则表示第 iii 号砖块是白色的,如果第 iii 个字符是 B,则表示第 iii 个砖块是黑色的。
输出格式
每组数据,如果无解则输出一行 −1−1−1。
否则,首先输出一行 kkk,表示需要的操作次数。
如果 k>0k>0k>0,则还需再输出一行 kkk 个整数,p1,p2,…,pkp_{1},p_{2},…,p_{k}p1,p2,…,pk。其中 pip_{i}pi 表示第 iii 次操作,选中的砖块为 pip_{i}pi 和 pi+1p_{i+1}pi+1 号砖块。
如果方案不唯一,则输出任意合理方案即可。
数据范围
1≤T≤101≤T≤101≤T≤10
2≤n≤2002≤n≤2002≤n≤200
输入样例
4
8
BWWWWWWB
4
BWBB
5
WWWWW
3
BWB
输出样例
3
6 2 4
-1
0
2
2 1
具体实现
1. 实现思路
- 并没有要求操作次数最少,因此,只需输出任意一组可成功操作的次数即可。最终的结果只有两种,要么全黑,要么全白, 两种情况可以依次枚举(任一情况都可)。
- 同一个位置我们最多操作 1 次,因为操作两次的话就变回原样。并且,操作的顺序不影响最后的结果。
- 其中,第一个砖块只能操作一次,所以,如果第一个砖块跟我们目标颜色相同的话,就不需要进行操作,如果不同的话,就一定会进行操作。第一个砖块是否操作是已经确定的了,第二个砖块也是同样的道理,后续皆同。因此在最后,如果最后一个砖块和目标颜色相同的话,就一定有解,如果不同的话就一定无解,这中间我们只需要操作 n-1 次。
2. 实现代码
#include <bits/stdc++.h>
using namespace std;
int n;
string str;
void update(char &c)
{if(c=='W'){c='B';}else{c='W';}
}
bool check(char c)
{vector<int>res;string s=str;for(int i=0;i<n-1;i++){if(s[i]!=c){update(s[i]);update(s[i+1]);res.push_back(i+1); //字符串从0开始,题目中从1开始}}if(s.back()!=c){return false;}cout<<res.size()<<endl;for(int x=0;x<res.size();x++){cout<<res[x]<<' ';}if(res.size()!=0){cout<<endl;}return true;
}
int main()
{int T;cin>>T;while(T--){cin>>n>>str;if(!check('B')&&!check('W')){cout<<"-1"<<endl;}}return 0;
}
相关文章:
)
AcWing - 蓝桥杯集训每日一题(DAY 1——DAY 5)
文章目录一、AcWing 3956. 截断数组(中等)1. 实现思路2. 实现代码二、AcWing 3729. 改变数组元素(中等)1. 实现思路2. 实现代码三、AcWing 1460. 我在哪?(简单)1. 实现思路2. 实现代码四、AcWin…...
)
RHCSA-文件的其他命令(3.7)
目录 文件的其他命令: 文本内容统计wc 移动和复制(cp) 移动 查找文件的路径 压缩和解压缩 .tar(归档命令) shell-命令解释器 linux中的特殊字符 查看系统上的别名:alias 历史命令(his…...

多线程update导致的mysql死锁问题处理方法
最近想起之前处理过的一个mysql 死锁问题,是在高并发下update批量更新导致的,这里探讨一下发生的原因,以及解决办法; 发生死锁的sql语句如下,其中where条件后的字段是有复合索引的。 update t_push_message_device_h…...
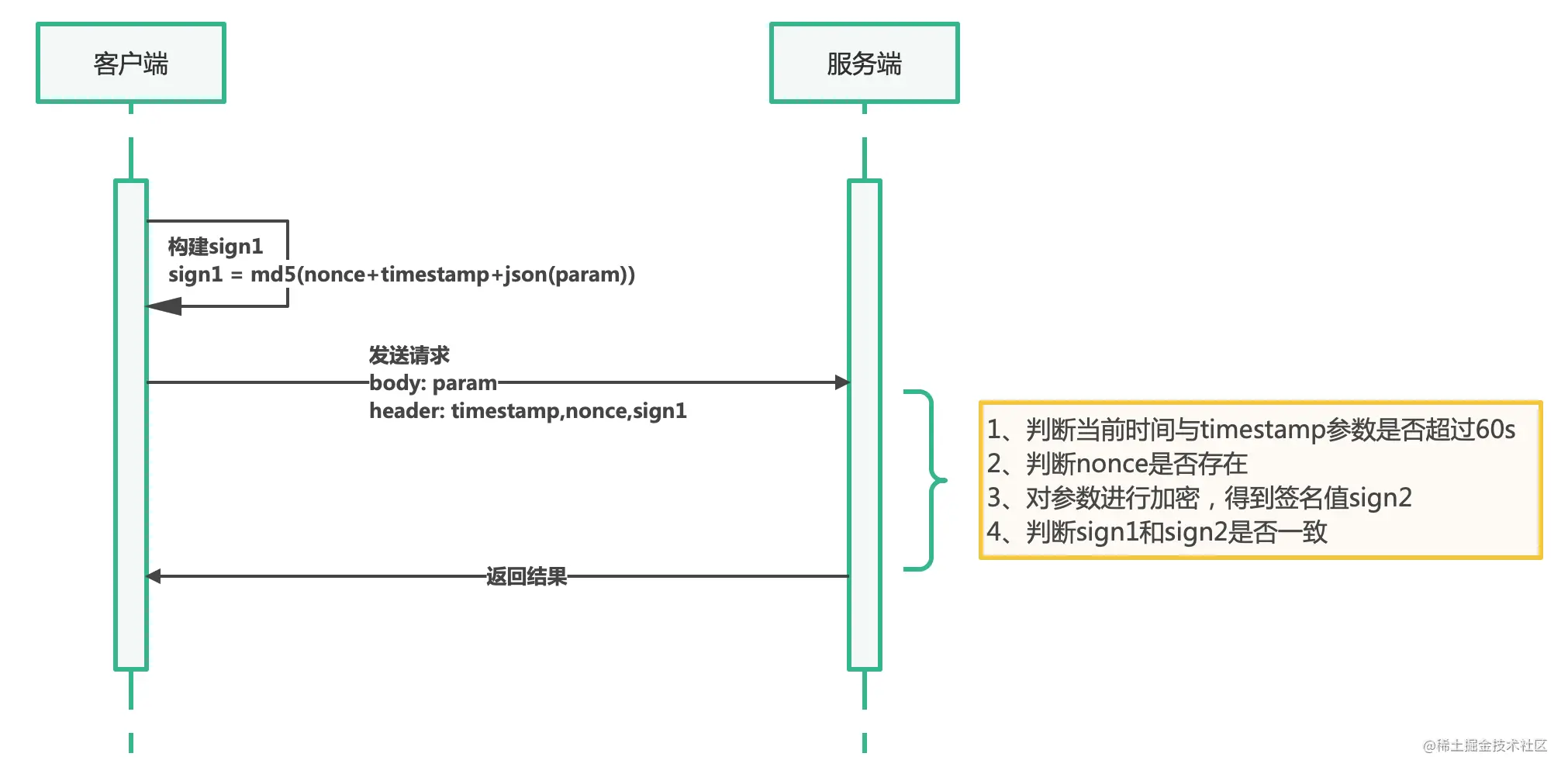
SpringBoot 如何保证接口安全?
为什么要保证接口安全对于互联网来说,只要你系统的接口暴露在外网,就避免不了接口安全问题。 如果你的接口在外网裸奔,只要让黑客知道接口的地址和参数就可以调用,那简直就是灾难。举个例子:你的网站用户注册的时候&am…...

英伟达驱动爆雷?CPU占用率过高怎么办?
又有一新驱动导致CPU占用率过高? 上周英伟达发布531.18显卡驱动,为大家带来了视频超分辨率技术,并为新发布的热门游戏《原子之心》提供支持。 但在安装新驱动后没过不久就有玩家反映,在游戏结束后会出现CPU占用率突然飙升到10%以…...
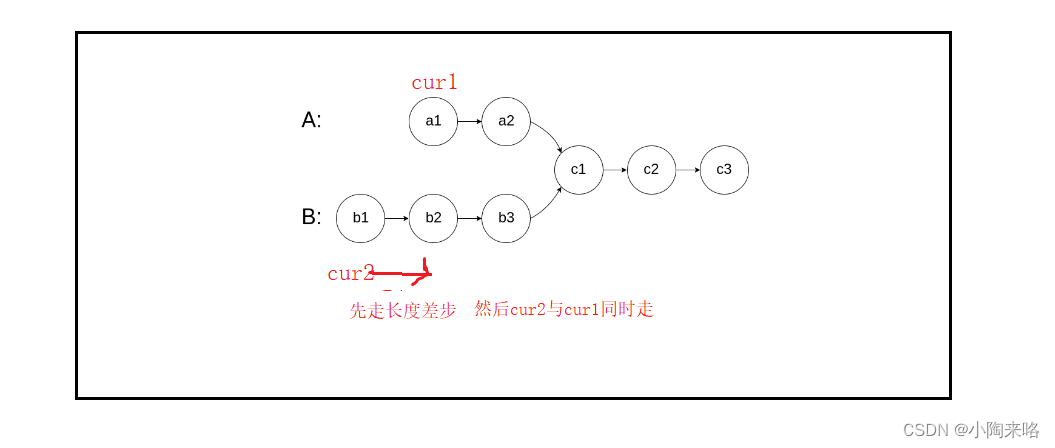
链表经典面试题【典中典】
💯💯💯链表经典面试题❗❗❗炒鸡经典,本篇带有图文解析,建议动手刷几遍。🟥1.反转链表🟧2.合并两个有序链表🟨3.链表分割🟩4.链表的回文结构🟦5.相交链表&…...

Java泛型深入
一. 泛型的概述和优势 泛型概述 泛型:是JDK5中引入的特性,可以在编译阶段约束操作的数据类型,并进行检查。泛型的格式:<数据类型>,注意:泛型只能支持引用数据类型。集合体系的全部接口和实现类都是…...
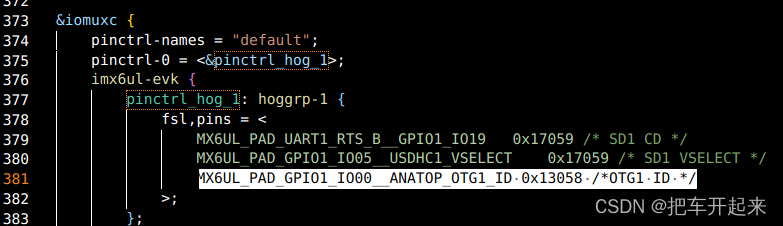
体验Linux USB 驱动
目录 一、USB OTG 二、I.MX6ULL USB 接口简介 硬件原理图 1、USB HUB 原理图 2 、USB OTG 原理图 三、使能驱动 1、打开 HID 驱动 2、 使能 USB 键盘和鼠标驱动 3 、使能 Linux 内核中的 SCSI 协议 4、使能 U 盘驱动 四、测试u盘 五、 Linux 内核自带 USB OTG USB 是…...

servlet 中的ServletConfig与servletContext
ServletConfig对象:servlet配置对象,主要把servlet的初始化参数封装到这个对象中。 一个网站中可能会存在多个servletConfig对象,一个servletConfig对象就封装了一个servlet的配置信息。 可以在web.xml中通过<init-param></init-p…...

Hadoop3.1.3单机(伪分布式配置)
参考:林子雨老师网站博客 Hadoop安装搭建伪分布式教程(全面)吐血整理 环境 Vmare12 Ubuntu16.04 创建Hadoop用户 若安装Ubuntu不是用的“hadoop”用户,则需要增加一个名为"hadoop"的用户 直接快捷键ctrlaltt或者点…...
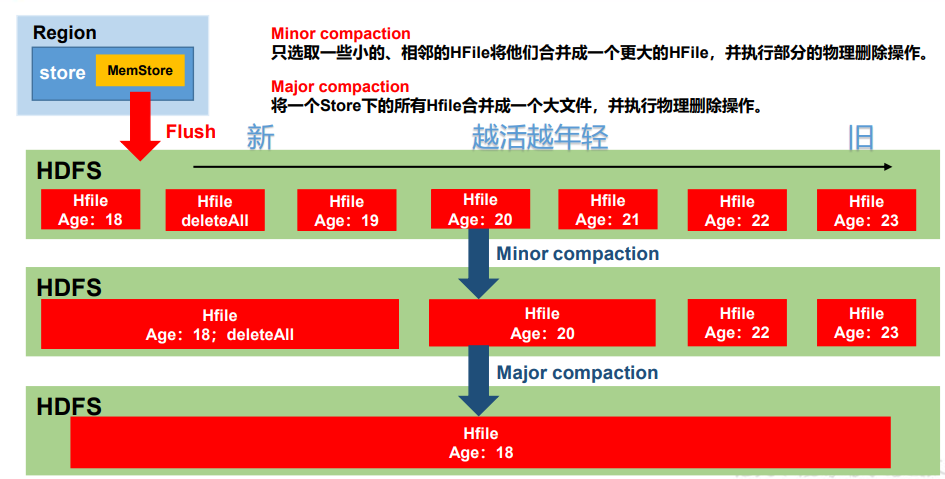
HBase---浅谈HBase原理
浅谈HBase原理 文章目录浅谈HBase原理HBase定义HBase逻辑结构HBase物理存储结构TimeStampType数据模型NaneSpaceRegionRowColumnTineStampCellHBase架构MasterMaster 架构Meta 表格介绍Region ServerRegionServer 架构MemStoreWALBlockCacheZookeeperHDFSHBase写数据流程HBase读…...

学习笔记四:dockerfile
Dockerfile概述dockerfile语法详解FROMMAINTAINERRUN:指定在当前镜像构建过程中要运行的命令EXPOSE指令CMDENTERYPOINTCOPYADDVOLUMEWORKDIRENVUSERONBUILDLABELHEALTHCHECKARG概述 Dockerfile 是一个用来构建镜像的文本文件,文本内容包含了一条条构建镜…...

微服务里的小问题
1.微服务为什么设置不同的namespace 为了实现三种服务三种情况下的隔离。 2.为什么要用nginx为naocos集群结点做负载均衡? 2.1 正向代理 就像我们访问外网需要一个代理。 2.2 反向代理 我们不需要访问真实的ip,只需要访问 这个服务的代理服务器即可&a…...
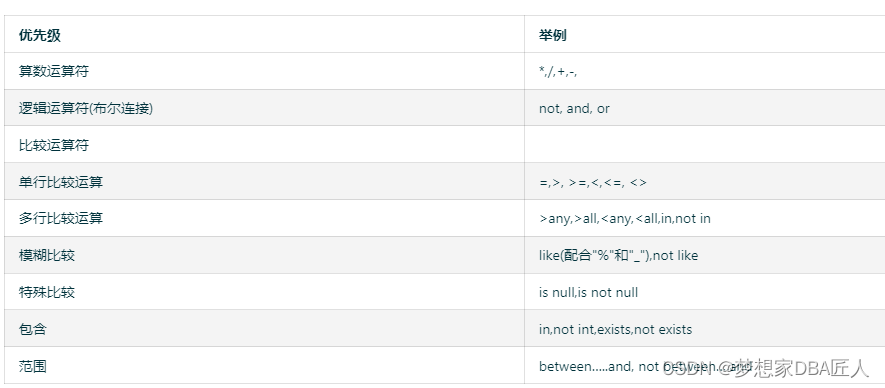
数据库之基本功:Where 中常用运算符
1. 运算符及优先级 ( )优先级最高 SQL> show user; USER is "SCOTT" SQL> select ename, job, sal, comm from emp where jobSALESMAN OR jobPRESIDENT and sal> 1500;ENAME JOB SAL COMM …...
浅谈 Nodejs原型链污染
一直在做php的题目,对其它语言做的很少。刚好在西湖论剑2022复现时,遇到了一道原型链污染的题目,借此机会开始简单学习一下 Nodejs的洞 p🐂讲解的十分清楚,因此下面举例子就直接用p🐂的例子进行解释了 目…...

Linux系统安装Docker
目录 Linux系统安装Docker 1、如果之前安装过旧版本的Docker,可以使用下面命令卸载 2、安装docker 3、启动docker 4、配置镜像加速 Linux系统安装Docker 前提:Docker CE 支持 64 位版本 CentOS 7,并且要求内核版本不低于 3.10࿰…...
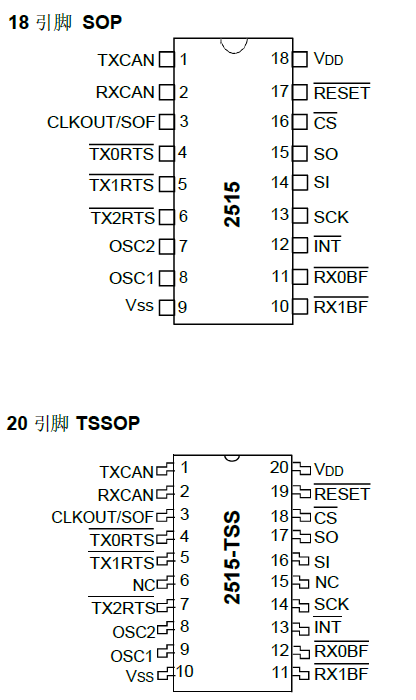
MCP2515国产替代DP2515带有SPI 接口的独立CAN 控制器
DP2515是一款独立控制器局域网络(Controller AreaNetwork, CAN)协议控制器,完全支持CAN V2.0B 技术规范。该器件能发送和接收标准和扩展数据帧以及远程帧。DP2515自带的两个验收屏蔽寄存器和六个验收滤波寄存器可以过滤掉不想要的…...

【Kubernetes】第二十篇 - k8s 污点和容忍度
一,前言 上一篇,介绍了 k8s ConfigMap 管理服务环境变量; 本篇,介绍 k8s 污点和容忍度; 二,污点与容忍度介绍 通过污点和容忍度配置可以干预 Pod 部署到特定的节点; 比如: 不想让…...

60% 程序员大呼:我要远程办公!
近几年数字化的普及,白领们从挤地铁、打卡、开会、写日报转变成“早上9点视频会议”,企业的办公场所也从写字楼、会议室、工位变成了手机、电脑中的线上会议室,远程办公已经成为一种流行的办公形式。《财富》杂志发现,75%的员工表…...
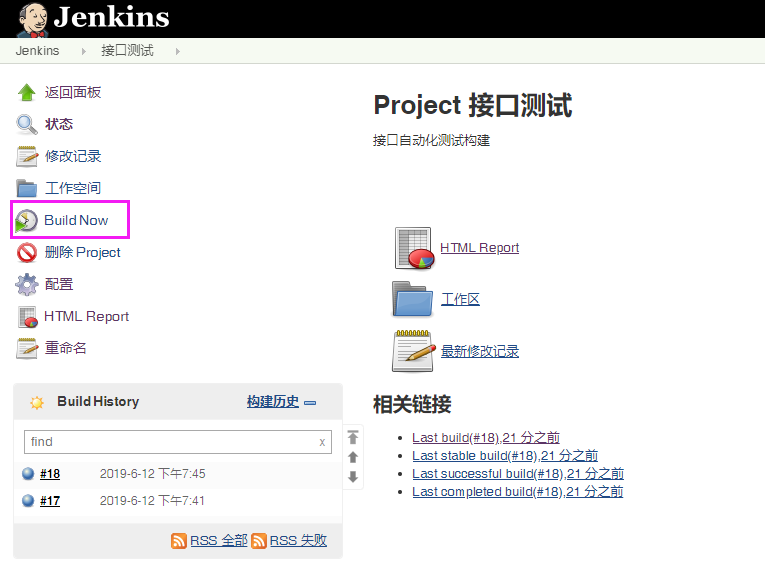
jmeter+ant+jenkins接口自动化测试框架
大致思路:Jmeter可以做接口测试,也能做压力测试,而且是开源软件;Ant是基与java的构建工具,完成脚本执行并收集结果生成报告,可以跨平台,Jenkins是持续集成工具。将这三者结合起来可以搭建一套We…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...
