javascript中的浅拷贝和深拷贝
浅拷贝:拷贝的是引用类型数据的第一层:数组或者对象:的地址
深拷贝:通过不断的递归进行拷贝
原理普及:在js中引用类型的变量储存的时候引用类型数据的地址,因此当地址被重新赋值新的对象的时候,修改新的对象,实际上就等于修改了原来的对象。因此浅拷贝的出现就是开辟一个新的地址去拷贝原来对象的数据,这样修改的时候 就不会影响到原来的数据了。
但是因为浅拷贝只能深究到第一层,因此就有了深拷贝的出现。
浅拷贝:
<script>// 浅拷贝 首先要知道深浅拷贝只针对引用数据类型// 浅拷贝拷贝的是引用类型的里面第一层的地址 储存空间中,有栈和堆 栈存放地址 堆存放内容// 实现浅拷贝有两种方式 第一种类似于解构const obj = {name:"ddd",age:18,hobby:"basketball",body:{foot:"foot",head:"head"}}const o = {...obj}console.log(o);console.log(obj);o.age = 20console.log(o);console.log(obj);// 第二种方式实现浅拷贝 Object.assgin() const obj2 = {name:"ddd",age:18,hobby:"basketball",body:{foot:"foot",head:"head"}}const o2 = {}Object.assign(o2,obj2)console.log(o2);console.log(obj2);
// 如果是数组 两种方法 对应就是[...xxx]和.concat()</script>深拷贝:
<script>// const obj = {// name:"ddd",// age:20,// hobby:["项目1","项目2"]// }// const o = {// }// function deepCopy (newObj,oldObj) {// // k是属性名 oldObj[k]属性值// for(let k in oldObj){// // 处理数组的问题// if(oldObj[k] instanceof Array){// newObj[k] = []// // 这里有点难理解 newObj[k]就是hobby数组 然后对这个数组进行操作// deepCopy (newObj[k],oldObj[k])// }else{// newObj[k] = oldObj[k]// }// }// }// deepCopy(o,obj) //o是新对象 obj是旧对象// console.log(o);// // 如果我修改了新对象里面的数组或者对象 新旧同时也会被修改 所以没有达到拷贝的效果 引用类型还是把地址拿来了// console.log(obj);// 第二种方式实现深拷贝// 然后引入// <script src="xxxx"><script>// const obj = {// name:"ddd",// age:20,// hobby:["项目1","项目2"]// }// const o = _.cloneDeep(obj)// console.log(o)//第三种方式深拷贝 JSONconst obj = {name:"ddd",age:20,hobby:["项目1","项目2"]}// 把对象转换为json字符串JSON.stringify(obj)console.log(JSON.stringify(obj));// JSON.parse(JSON.stringify(obj)) 又把json字符串转换为了对象 但是这个时候的对象 等于在空间有开辟了一个新的地址 const o = JSON.parse(JSON.stringify(obj))//完美实现深拷贝console.log(o);o.hobby.push("dddddd")console.log(o);console.log(obj);</script>相关文章:

javascript中的浅拷贝和深拷贝
浅拷贝:拷贝的是引用类型数据的第一层:数组或者对象:的地址 深拷贝:通过不断的递归进行拷贝 原理普及:在js中引用类型的变量储存的时候引用类型数据的地址,因此当地址被重新赋值新的对象的时候ÿ…...

vue 实现自定义分页打印 window.print
首先这里是我自定义了打印界面才实现的效果,如果不用自定义界面实现,应该是一样的吧。具体可能需要自己去试试看 我的需求是界面有两个表格,点击全部打印,我需要把第一表格在打印是第1页,第二个表格是第二页 如图&…...

基于 Erlang 的随机账户分配机制
当你在网上注册新账户时,平台如何为你生成一个独特的用户名或编号呢?这背后其实有一套精心设计的系统。本文将带你了解一种使用 Erlang 语言开发的随机账户分配系统,它既快速又可靠。 ## 随机分配的简单步骤 我们可以将这个过程想象成一个装…...

数码论坛系统的设计与实现|Springboot+ Mysql+Java+ B/S结构(可运行源码+数据库+设计文档)电子科技数码爱好者交流信息新闻畅聊讨论评价
本项目包含可运行源码数据库LW,文末可获取本项目的所有资料。 推荐阅读300套最新项目持续更新中..... 最新ssmjava项目文档视频演示可运行源码分享 最新jspjava项目文档视频演示可运行源码分享 最新Spring Boot项目文档视频演示可运行源码分享 2024年56套包含ja…...

时序预测 | Matlab实现CPO-LSTM【24年新算法】冠豪猪优化长短期记忆神经网络时间序列预测
时序预测 | Matlab实现CPO-LSTM【24年新算法】冠豪猪优化长短期记忆神经网络时间序列预测 目录 时序预测 | Matlab实现CPO-LSTM【24年新算法】冠豪猪优化长短期记忆神经网络时间序列预测效果一览基本介绍程序设计参考资料 效果一览 基本介绍 1.Matlab实现CPO-LSTM【24年新算法】…...

探索设计模式的魅力:AI大模型如何赋能C/S模式,开创服务新纪元
🌈 个人主页:danci_ 🔥 系列专栏:《设计模式》 💪🏻 制定明确可量化的目标,坚持默默的做事。 AI大模型如何赋能C/S模式,开创服务新纪元 数字化飞速发展的时代,AI大模型…...

2024年NAND价格市场继续上涨
TrendForce发布了最新的NAND闪存市场价格走势预测。根据其报告,在2024年第二季度,NAND闪存合同价格将进一步呈现两位数的增长,叠加前一季度的增长。不过,客户端SSD的价格涨幅预计在第二季度将不超过15%,相比于2024年第…...

分布式算法 - ZAB算法
ZAB算法是用于实现分布式系统中的原子广播的核心算法,它被广泛应用于ZooKeeper分布式协调服务中。 ZAB算法由两个主要阶段组成:崩溃恢复阶段和消息广播阶段。 在崩溃恢复阶段,当一个ZooKeeper节点启动或者领导者节点崩溃重启时,…...
Java设计之道:色即是空,空即是色
0.引子 我们的这个世界上,存在这么一种东西: 第一:它不占据任何3D之体积,即它没有Volume第二:它也不占据任何2D之面积,即它没有Area第三:它也不占据任何1D之长度,即它没有Length 总…...
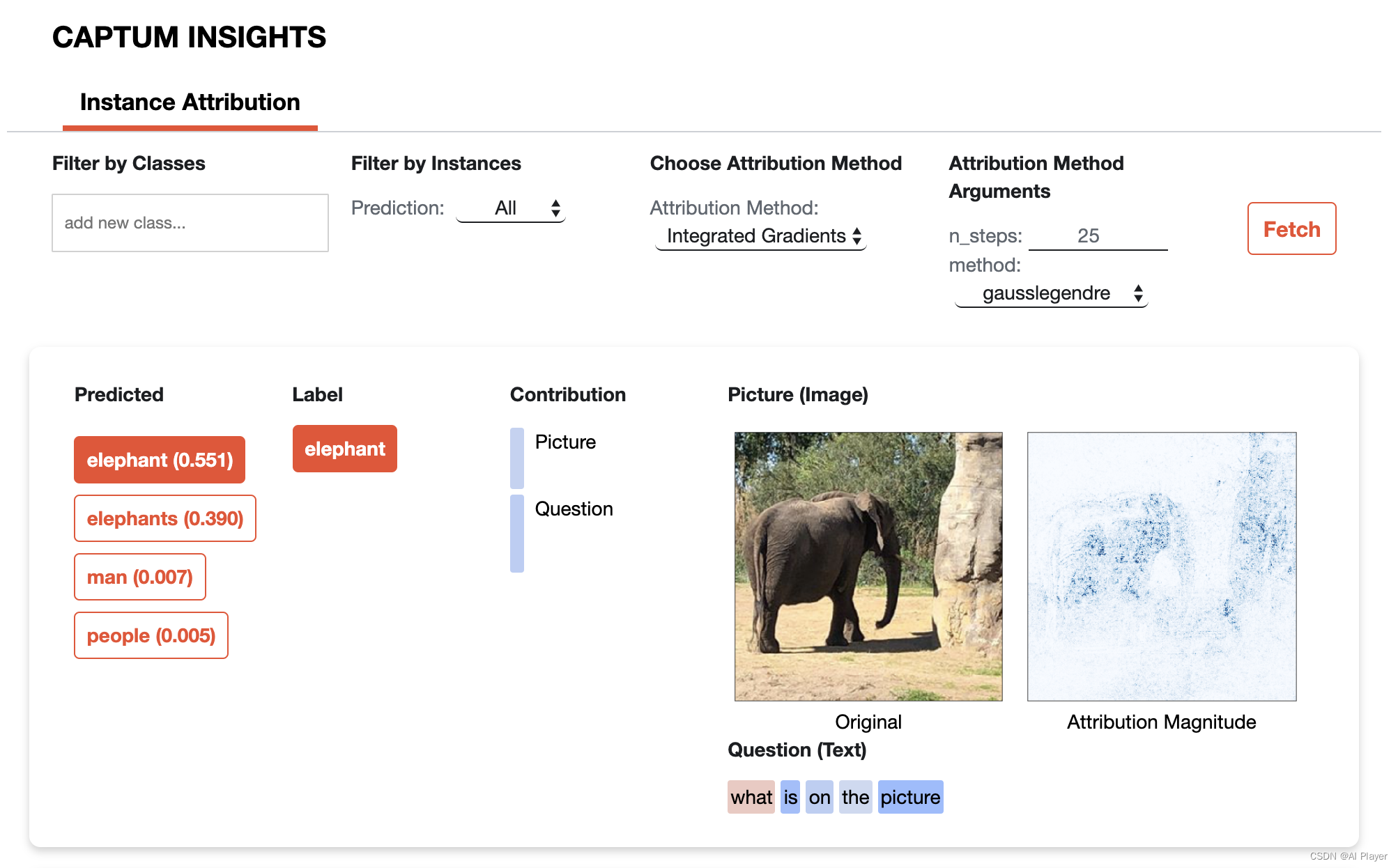
深度学习:基于PyTorch的模型解释工具Captum
深度学习:基于PyTorch的模型解释工具Captum 引言简介示例安装解释模型的预测解释文本模型情绪分析问答 解释视觉模型特征分析特征消融鲁棒性 解释多模态模型 引言 当我们训练神经网络模型时,我们通常只关注模型的整体性能,例如准确率或损失函…...

公司官网怎么才会被百度收录
在互联网时代,公司官网是企业展示自身形象、产品与服务的重要窗口。然而,即使拥有精美的官网,如果不被搜索引擎收录,就无法被用户发现。本文将介绍公司官网如何被百度收录的一些方法和步骤。 1. 创建和提交网站地图 创建网站地图…...
)
机器学习模型——SVM(支持向量机)
基本概念: Support Vector Machine (支持向量机): 支持向量:支持或支撑平面上把两类类别划分开来的超平面的向量点。 机:一个算法 SVM是基于统计学习理论的一种机器学习方法。简单地说,就是将数据单元…...

服务器CPU使用过高的原因
大多使用服务器的站长都会碰见这样的问题,在长时间使用后,系统越来越慢,甚至出现卡死或强制重启的情况。打开后台 才发现,CPU使用率已经快要到达90%。那么,我告诉你哪些因素会导致服务器CPU高使用率,从而严…...
基于tensorflow和kereas的孪生网络推理图片相似性
一、环境搭建 基础环境:cuda 11.2 python3.8.13 linux ubuntu18.04 pip install tensorflow-gpu2.11.0 验证:# 查看tensorflow版本 import tensorflow as tf tf.__version__ # 是否能够成功启动GPU from tensorflow.python.client import device_lib pr…...

day4|gin的中间件和路由分组
中间件其实是一个方法, 在.use就可以调用中间件函数 r : gin.Default()v1 : r.Group("v1")//v1 : r.Group("v1").Use()v1.GET("test", func(c *gin.Context) {fmt.Println("get into the test")c.JSON(200, gin.H{"…...

nodejs的express负载均衡
我们知道nodejs是单线程的,在特定场合是不能利用CPU多核的优势的。一般有两种方式来解决,一种是利用nodejs的cluster模块创建多个子进程来处理请求以充分利用cpu的多核,还有一种是nodejs运行多个服务分别监听在不同的port,利用nginx创建一个u…...

计算机网络-HTTP相关知识-RSA和ECDHE及优化
HTTPS建立基本流程 客户端向服务器索要并验证服务器的公钥。通过密钥交换算法(如RSA或ECDHE)协商会话秘钥,这个过程被称为“握手”。双方采用会话秘钥进行加密通信。 RSA流程 RSA流程包括四次握手: 第一次握手:客户…...
axios 封装 http 请求详解
前言 Axios 是一个基于 Promise 的 HTTP 库,它的概念及使用方法本文不过多赘述,请参考:axios传送门 本文重点讲述下在项目中是如何利用 axios 封装 http 请求。 一、预设全局变量 在 /const/preset.js 中配置预先设置一些全局变量 window.…...

牛客2024年愚人节比赛(A-K)
比赛链接 毕竟是娱乐场,放平心态打吧。。。 只有A一个考了数学期望,其他的基本都是acmer特有的脑筋急转弯,看个乐呵即可。 A 我是欧皇,赚到盆满钵满! 思路: 我们有 p 1 p_1 p1 的概率直接拿到一件实…...

loadbalancer 引入与使用
在消费中pom中引入 <dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-starter-loadbalancer</artifactId> </dependency> 请求调用加 LoadBalanced 注解 进行服务调用 默认负载均衡是轮训模式 想要切换…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...

Linux 下 DMA 内存映射浅析
序 系统 I/O 设备驱动程序通常调用其特定子系统的接口为 DMA 分配内存,但最终会调到 DMA 子系统的dma_alloc_coherent()/dma_alloc_attrs() 等接口。 关于 dma_alloc_coherent 接口详细的代码讲解、调用流程,可以参考这篇文章,我觉得写的非常…...

算术操作符与类型转换:从基础到精通
目录 前言:从基础到实践——探索运算符与类型转换的奥秘 算术操作符超级详解 算术操作符:、-、*、/、% 赋值操作符:和复合赋值 单⽬操作符:、--、、- 前言:从基础到实践——探索运算符与类型转换的奥秘 在先前的文…...

Monorepo架构: Nx Cloud 扩展能力与缓存加速
借助 Nx Cloud 实现项目协同与加速构建 1 ) 缓存工作原理分析 在了解了本地缓存和远程缓存之后,我们来探究缓存是如何工作的。以计算文件的哈希串为例,若后续运行任务时文件哈希串未变,系统会直接使用对应的输出和制品文件。 2 …...

基于单片机的宠物屋智能系统设计与实现(论文+源码)
本设计基于单片机的宠物屋智能系统核心是实现对宠物生活环境及状态的智能管理。系统以单片机为中枢,连接红外测温传感器,可实时精准捕捉宠物体温变化,以便及时发现健康异常;水位检测传感器时刻监测饮用水余量,防止宠物…...
