PTA:C课程设计(2)
山东大学(威海)2022级大一下C习题集(2)
- 2-5-1 字符定位函数(程序填空题)
- 2-5-2 判断回文(程序填空题)
- 2-6-1 数字金字塔(函数)
- 2-6-2 使用函数求最大公约数(函数)
- 2-6-3 使用函数求余弦函数的近似值(函数)
- 2-6-4 使用函数输出水仙花数(函数)
- 2-6-5 使用函数的选择法排序(函数)
- 2-7-1 求一批整数中出现最多的个位数字
- 2-7-2 找鞍点
2-5-1 字符定位函数(程序填空题)
在主函数中输入一个字符串和一个字符,调用match函数,如果该字符在字符串中,就从该字符首次出现的位置开始输出字符串中的字符。如果未找到,输出“Not Found”。
本题要求:根据main函数的程序实现,完成match函数的定义。
int main(void )
{char ch, str[80], *p = NULL;scanf("%s", str);getchar(); while((ch = getchar())!='\n') {if((p = match(str, ch)) != NULL) printf("%s\n", p);else printf("Not Found\n");}return 0;
}
//1)____________________ (1分)/* 字符定位函数定义:match函数*/
{while (/*2)________ (1分) */)if (*s == ch) //3)__________ (1分) else s++; return //4)__________ (1分);
}
答案:
1)char* match(char* s,char ch)
2)*s!='\0'
3)return s;
4) NULL
2-5-2 判断回文(程序填空题)
回文是指正读和反读都一样的字符串,如abcba就是一个回文,
从键盘输入一个字符串判断其是否是回文,如果是则输出"Yes!“,
否则输出"No!”,请填空完成相应功能。
输入输出样例如下:
输入样例1:
abccba
输出样例1:
Yes!
输入样例2:
abcde
输出样例2:
No!
#include <stdio.h>
#include <string.h>
#define N 80
int main(void)
{char s[N];int i,j;gets(s); i=0;j = /*1)_________ (1分)*/;while(/*2)_________ (1分)*/){if(/*3)_________ (1分)*/){i++;j--;}elsebreak;
}if(/*4)_________ (1分)*/)printf("Yes!\n");elseprintf("No!\n");return 0;
}
1)strlen(s)-1
2)i<j
3)s[i] == s[j]
4)i>=j
2-6-1 数字金字塔(函数)
函数接口定义:
void pyramid(int n);
其中n是用户传入的参数,为[1, 9]的正整数。要求函数按照如样例所示的格式打印出n行数字金字塔。注意每个数字后面跟一个空格。
void pyramid(int n)
{for (int i = 1; i <= n; i++){for (int k = 0; k < n - i; k++)printf(" ");for (int j = 1; j <= i; j++){printf("%d ", i);}printf("\n");}
}2-6-2 使用函数求最大公约数(函数)
函数接口定义:
int gcd( int x, int y );
其中x和y是两个正整数,函数gcd应返回这两个数的最大公约数
int gcd( int x, int y )
{int ret = 0;if(x>=y){if(x%y==0)return y;elsereturn gcd(y,x%y);}else{if(y%x==0)return x;elsereturn gcd(x,y%x);}
}
2-6-3 使用函数求余弦函数的近似值(函数)
函数接口定义:
double funcos( double e, double x );
本题要求实现一个函数,用麦克劳林展开公式求cos(x)的近似值,精确到最后一项的绝对值小于e(函数的一个参数,不是数学中的那个e)
double funcos( double e, double x )
{if(x==0)return 1;double fu = 1.0,t = 1.0;double sum = 1.0;int i = 1;while(t>=e){fu = -1*fu*x*x/(i*(i+1));i+=2;sum+=fu;if(fu<0)t = -1*fu;elset = fu;}return sum;
}
2-6-4 使用函数输出水仙花数(函数)
函数接口定义:
int narcissistic( int number );
void PrintN( int m, int n );
函数narcissistic判断number是否为水仙花数,是则返回1,否则返回0。
函数PrintN则打印开区间(m, n)内所有的水仙花数,每个数字占一行。题目保证100≤m≤n≤10000
int narcissistic( int number )
{int count = 0;int n = number,t = number;while(n){count++;n/=10;}int sum = 0,w = 0;for(int i = 0;i<count;i++){w=number%10;sum += pow(w,count);number/=10;}if(t==sum)return 1;return 0;}void PrintN( int m, int n )
{for(int i = m+1;i<n;i++){if(narcissistic(i))printf("%d\n",i);}
}
2-6-5 使用函数的选择法排序(函数)
函数接口定义:
void sort( int a[], int n );
其中a是待排序的数组,n是数组a中元素的个数。该函数用选择法将数组a中的元素按升序排列,结果仍然在数组a中。
void sort( int a[], int n )
{for(int j = 0;j<n-1;j++){int min = a[j];for(int i = 0;i<n-1-j;i++){if(a[i]>a[i+1]){int t = a[i];a[i] = a[i+1];a[i+1] = t;}}}
}
2-7-1 求一批整数中出现最多的个位数字
给定一批整数,分析每个整数的每一位数字,求出现次数最多的个位数字。例如给定3个整数1234、2345、3456,其中出现最多次数的数字是3和4,均出现了3次。
输入格式:
输入在第1行中给出正整数N(≤1000),在第二行中给出N个不超过整型范围的非负整数,数字间以空格分隔。
输出格式:
在一行中按格式“M: n1 n2 …”输出,其中M是最大次数,n1、n2、……为出现次数最多的个位数字,按从小到大的顺序排列。数字间以空格分隔,但末尾不得有多余空格。
#include<stdio.h>
#include<ctype.h>int main()
{int n = 0;int i, max =0, c, m;int arr[10] = {0};while (scanf("%d", &n) != EOF) {max = 0;for (i = 0; i<10; i++) {arr[i] = 0;}for (i = 0; i < n; i++) {scanf("%d", &c);do {m = c % 10;c /= 10;arr[m]++;if (arr[m] > max) {max = arr[m];}} while (c);}printf("%d:", max);for (int j = 0; j<10; j++) {if (arr[j] == max) {printf(" %d", j);}}printf("\n");}return 0;
}2-7-2 找鞍点
一个矩阵元素的“鞍点”是指该位置上的元素值在该行上最大、在该列上最小。
本题要求编写程序,求一个给定的n阶方阵的鞍点。
输入格式:
输入第一行给出一个正整数n(1≤n≤6)。随后n行,每行给出n个整数,其间以空格分隔。
输出格式:
输出在一行中按照“行下标 列下标”(下标从0开始)的格式输出鞍点的位置。如果鞍点不存在,则输出“NONE”。题目保证给出的矩阵至多存在一个鞍点
#include<stdio.h>
int main()
{int n = 0;scanf("%d",&n);int arr[6][6];for(int i = 0;i<n;i++){for(int j = 0;j<n;j++)scanf("%d",&arr[i][j]);}int h = 0,l=0,flag =0;int i = 0;for(;i<n;i++){for(int j = 0;j<n;j++){if(arr[i][j]>=arr[i][l]){l = j;}}flag = 1;for(h = 0;h<n;h++){if(arr[h][l] <arr[i][l]){flag = 0;break;}}if(flag ==1)break;}if(flag == 1){printf("%d %d",i,l);}elseprintf("NONE");return 0;
}
相关文章:
)
PTA:C课程设计(2)
山东大学(威海)2022级大一下C习题集(2)2-5-1 字符定位函数(程序填空题)2-5-2 判断回文(程序填空题)2-6-1 数字金字塔(函数)2-6-2 使用函数求最大公约数(函数)2-6-3 使用函数求余弦函…...
第四章:面向对象编程
第四章:面向对象编程 4.1:面向过程与面向对象 面向过程(POP)与面向对象(OOP) 二者都是一种思想,面向对象是相对于面向过程而言的。面向过程,强调的是功能行为,以函数为最小单位,考虑怎么做。面向对象&…...

Linux 安装npm yarn pnpm 命令
下载安装包 node 下载地址解压压缩包 tar -Jxf node-v19.7.0-linux-x64.tar.xz -C /root/app echo "export PATH$PATH:/app/node-v16.9.0-linux-x64" >> /etc/profile source /etc/profile ln -sf /app/node-v16.9.0-linux-x64/bin/npm /usr/local/bin/ ln -…...
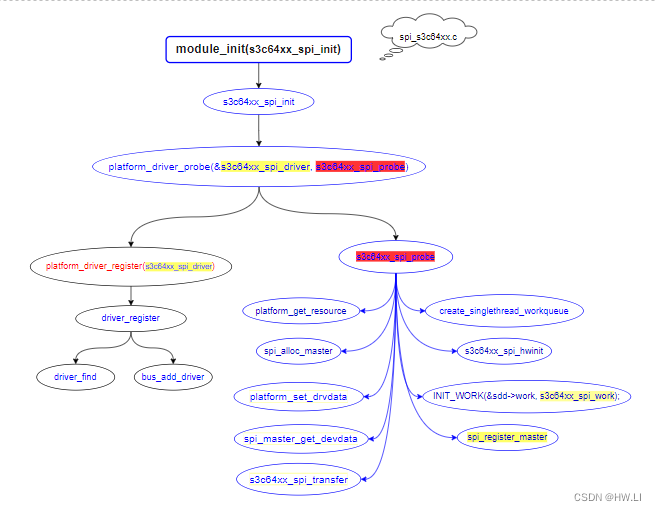
linux SPI驱动代码追踪
一、Linux SPI 框架概述 linux系统下的spi驱动程序从逻辑上可以分为3个部分: SPI Core:SPI Core 是 Linux 内核用来维护和管理 spi 的核心部分,SPI Core 提供操作接口,允许一个 spi master,spi driver 和 spi device 在 SPI Cor…...

Ls-dyna材料的相关学习笔记
Elastic Linear elastic materials -Isotropic:各向同性材料 -orthotropic 正交各向异性的 -anistropic 各向异性的...
)
Arrays方法(copyOfRange,fill)
Arrays方法 1、Arrays.copyOfRange Arrays.copyOfRange的使用方法 功能: 将数组拷贝至另外一个数组 参数: original:第一个参数为要拷贝的数组对象 from:第二个参数为拷贝的开始位置(包含) to:…...
)
AcWing - 蓝桥杯集训每日一题(DAY 1——DAY 5)
文章目录一、AcWing 3956. 截断数组(中等)1. 实现思路2. 实现代码二、AcWing 3729. 改变数组元素(中等)1. 实现思路2. 实现代码三、AcWing 1460. 我在哪?(简单)1. 实现思路2. 实现代码四、AcWin…...
)
RHCSA-文件的其他命令(3.7)
目录 文件的其他命令: 文本内容统计wc 移动和复制(cp) 移动 查找文件的路径 压缩和解压缩 .tar(归档命令) shell-命令解释器 linux中的特殊字符 查看系统上的别名:alias 历史命令(his…...

多线程update导致的mysql死锁问题处理方法
最近想起之前处理过的一个mysql 死锁问题,是在高并发下update批量更新导致的,这里探讨一下发生的原因,以及解决办法; 发生死锁的sql语句如下,其中where条件后的字段是有复合索引的。 update t_push_message_device_h…...
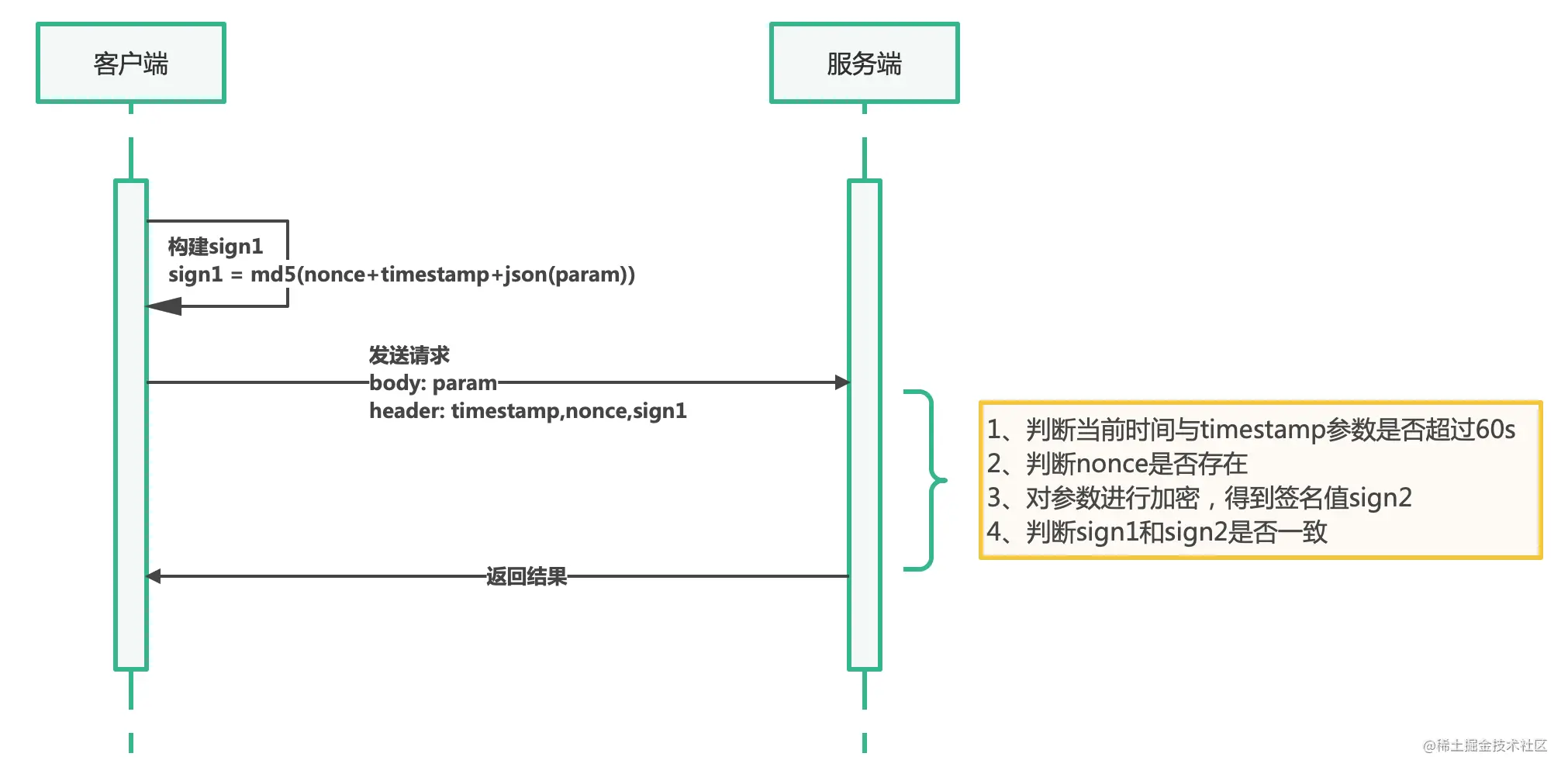
SpringBoot 如何保证接口安全?
为什么要保证接口安全对于互联网来说,只要你系统的接口暴露在外网,就避免不了接口安全问题。 如果你的接口在外网裸奔,只要让黑客知道接口的地址和参数就可以调用,那简直就是灾难。举个例子:你的网站用户注册的时候&am…...

英伟达驱动爆雷?CPU占用率过高怎么办?
又有一新驱动导致CPU占用率过高? 上周英伟达发布531.18显卡驱动,为大家带来了视频超分辨率技术,并为新发布的热门游戏《原子之心》提供支持。 但在安装新驱动后没过不久就有玩家反映,在游戏结束后会出现CPU占用率突然飙升到10%以…...
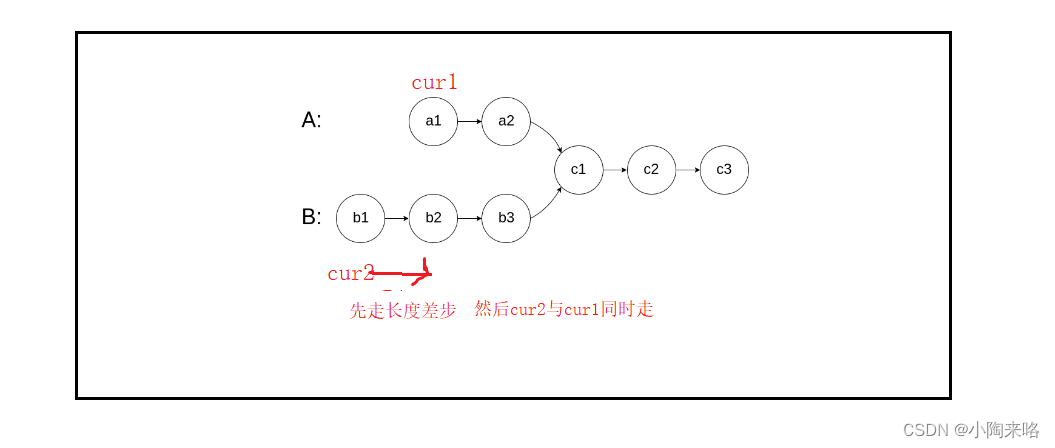
链表经典面试题【典中典】
💯💯💯链表经典面试题❗❗❗炒鸡经典,本篇带有图文解析,建议动手刷几遍。🟥1.反转链表🟧2.合并两个有序链表🟨3.链表分割🟩4.链表的回文结构🟦5.相交链表&…...

Java泛型深入
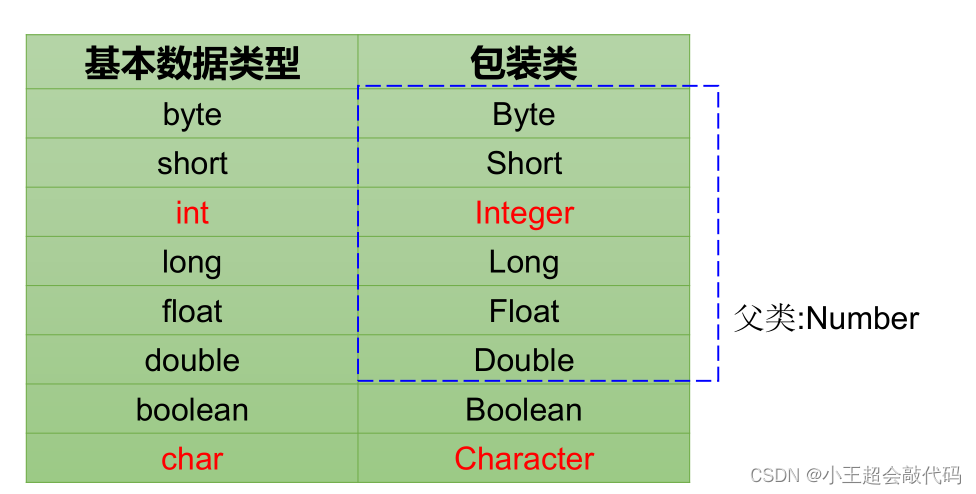
一. 泛型的概述和优势 泛型概述 泛型:是JDK5中引入的特性,可以在编译阶段约束操作的数据类型,并进行检查。泛型的格式:<数据类型>,注意:泛型只能支持引用数据类型。集合体系的全部接口和实现类都是…...
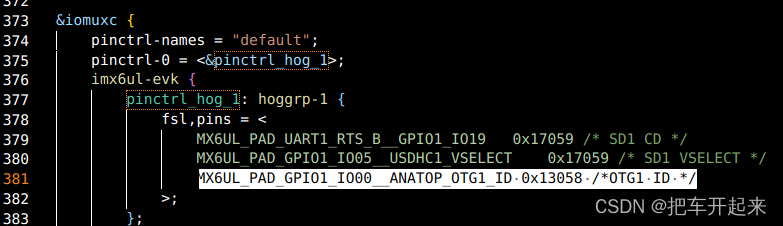
体验Linux USB 驱动
目录 一、USB OTG 二、I.MX6ULL USB 接口简介 硬件原理图 1、USB HUB 原理图 2 、USB OTG 原理图 三、使能驱动 1、打开 HID 驱动 2、 使能 USB 键盘和鼠标驱动 3 、使能 Linux 内核中的 SCSI 协议 4、使能 U 盘驱动 四、测试u盘 五、 Linux 内核自带 USB OTG USB 是…...

servlet 中的ServletConfig与servletContext
ServletConfig对象:servlet配置对象,主要把servlet的初始化参数封装到这个对象中。 一个网站中可能会存在多个servletConfig对象,一个servletConfig对象就封装了一个servlet的配置信息。 可以在web.xml中通过<init-param></init-p…...

Hadoop3.1.3单机(伪分布式配置)
参考:林子雨老师网站博客 Hadoop安装搭建伪分布式教程(全面)吐血整理 环境 Vmare12 Ubuntu16.04 创建Hadoop用户 若安装Ubuntu不是用的“hadoop”用户,则需要增加一个名为"hadoop"的用户 直接快捷键ctrlaltt或者点…...
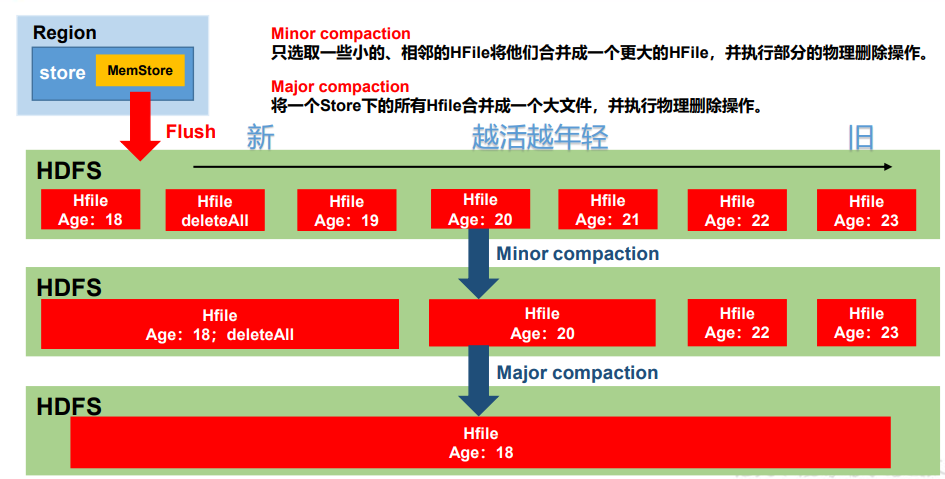
HBase---浅谈HBase原理
浅谈HBase原理 文章目录浅谈HBase原理HBase定义HBase逻辑结构HBase物理存储结构TimeStampType数据模型NaneSpaceRegionRowColumnTineStampCellHBase架构MasterMaster 架构Meta 表格介绍Region ServerRegionServer 架构MemStoreWALBlockCacheZookeeperHDFSHBase写数据流程HBase读…...

学习笔记四:dockerfile
Dockerfile概述dockerfile语法详解FROMMAINTAINERRUN:指定在当前镜像构建过程中要运行的命令EXPOSE指令CMDENTERYPOINTCOPYADDVOLUMEWORKDIRENVUSERONBUILDLABELHEALTHCHECKARG概述 Dockerfile 是一个用来构建镜像的文本文件,文本内容包含了一条条构建镜…...

微服务里的小问题
1.微服务为什么设置不同的namespace 为了实现三种服务三种情况下的隔离。 2.为什么要用nginx为naocos集群结点做负载均衡? 2.1 正向代理 就像我们访问外网需要一个代理。 2.2 反向代理 我们不需要访问真实的ip,只需要访问 这个服务的代理服务器即可&a…...
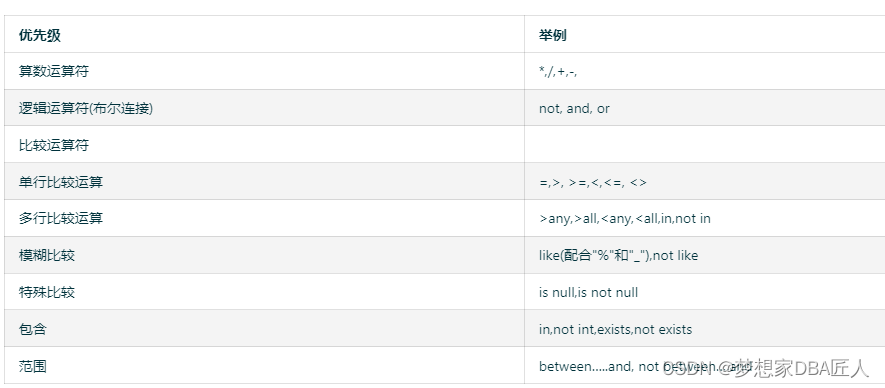
数据库之基本功:Where 中常用运算符
1. 运算符及优先级 ( )优先级最高 SQL> show user; USER is "SCOTT" SQL> select ename, job, sal, comm from emp where jobSALESMAN OR jobPRESIDENT and sal> 1500;ENAME JOB SAL COMM …...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...
