【蓝桥杯集训·每日一题】AcWing 3305. 作物杂交
文章目录
- 一、题目
- 1、原题链接
- 2、题目描述
- 二、解题报告
- 1、思路分析
- 2、时间复杂度
- 3、代码详解
- 三、知识风暴
- Spfa算法
一、题目
1、原题链接
3305. 作物杂交
2、题目描述
作物杂交是作物栽培中重要的一步。
已知有 N 种作物 (编号 1 至 N),第 i 种作物从播种到成熟的时间为 Ti。
作物之间两两可以进行杂交,杂交时间取两种中时间较长的一方。
如作物 A 种植时间为 5 天,作物 B 种植时间为 7 天,则 AB 杂交花费的时间为 7 天。
作物杂交会产生固定的作物,新产生的作物仍然属于 N 种作物中的一种。
初始时,拥有其中 M 种作物的种子 (数量无限,可以支持多次杂交)。
同时可以进行多个杂交过程。
求问对于给定的目标种子,最少需要多少天能够得到。
如存在 4 种作物 ABCD,各自的成熟时间为 5 天、7 天、3 天、8 天。
初始拥有 AB 两种作物的种子,目标种子为 D,已知杂交情况为 A×B→C,A×C→D。
则最短的杂交过程为:
第 1 天到第 7 天 (作物 B 的时间),A×B→C。
第 8 天到第 12 天 (作物 A 的时间),A×C→D。
花费 12 天得到作物 D 的种子。
输入格式
输入的第 1 行包含 4 个整数 N,M,K,T,N 表示作物种类总数 (编号 1 至 N),M 表示初始拥有的作物种子类型数量,K
表示可以杂交的方案数,T 表示目标种子的编号。第 2 行包含 N 个整数,其中第 i 个整数表示第 i 种作物的种植时间 Ti。
第 3 行包含 M 个整数,分别表示已拥有的种子类型 Kj,Kj 两两不同。
第 4 至 K+3 行,每行包含 3 个整数 A,B,C,表示第 A 类作物和第 B 类作物杂交可以获得第 C 类作物的种子。
输出格式
输出一个整数,表示得到目标种子的最短杂交时间。
样例解释
1≤N≤2000,2≤M≤N,1≤K≤105,1≤T≤N,1≤Ti≤100,1≤Kj≤M,
保证目标种子一定可以通过杂交得到。
不保证作物 A 和 B 杂交只能生成作物 C(也就是说,A×B→C 和 A×B→D 可能同时在输入中出现)
不保证作物 C 只能由作物 A 和 B 杂交生成(也就是说,A×B→D 和 A×C→D 可能同时在输入中出现)。
不保证同一杂交公式不在输入中重复出现。输入样例:
6 2 4 6 5 3 4 6 4 9 1 2 1 2 3 1 3 4 2 3 5 4 5 6输出样例:
16样例解释
第 1 天至第 5 天,将编号 1 与编号 2 的作物杂交,得到编号 3 的作物种子。
第 6 天至第 10 天,将编号 1 与编号 3 的作物杂交,得到编号 4 的作物种子。
第 6 天至第 9 天,将编号 2 与编号 3 的作物杂交,得到编号 5 的作物种子。
第 11 天至第 16 天,将编号 4 与编号 5 的作物杂交,得到编号 6 的作物种子。
总共花费 16 天。
二、解题报告
1、思路分析
思路来源:y总讲解视频
y总yyds
动态规划解法(spfa思想求解)
(1)dist数组含义:dist[i][j]表示在杂交次数小于等于i的方法中,生成j所需花费的最小时间。
(2)按最后一次的杂交方式进行划分,最多可以分为k种。
(3)转移方程:当最后一次杂交(假设为A、B杂交)确定后,要使总时间最小,则使将A、B都生成所花费的时间最小即可。即 dist[i][j]=max(dist[i-1][A],dist[i-1][B])+max(T[A],T[B])(T[i]代表生成i需要花费的时间)。
(4)利用spfa进行优化:只有一个点被更新过才需要利用它来更新其他点,并且dist[][]的第一维可以被优化。
(5)利用上述思路进行模拟即可,输出dist[t]即为答案。
2、时间复杂度
时间复杂度为O(n*k)
3、代码详解
#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
const int N=2010,M=200010; //N代表点数(作物数),M代表边数,每种作物最多可能有k种杂交方式,所以M开成N*k数量级
int h[N],e[M],ne[M],w[N],target[M],idx; //类似邻接表存储所有的杂交方式,w[]存储生成每种作物需要花费的时间,target[i]存储利用i杂交可以生成的目标种子,w[i]存储生成i需要的时间
int n,m,k,t;
int dist[N];
bool st[N];
queue<int> q;
//类似邻接表加边
void add(int a,int b,int c){e[idx]=b;target[idx]=c;ne[idx]=h[a];h[a]=idx++;
}
//spfa思路来填充dist数组
void spfa(){while(!q.empty()){int A=q.front();q.pop();st[A]=false;for(int i=h[A];i!=-1;i=ne[i]){int B=e[i],T=target[i];if(dist[T]>max(dist[A],dist[B])+max(w[A],w[B])){dist[T]=max(dist[A],dist[B])+max(w[A],w[B]);if(!st[T]){st[T]=true;q.push(T);}}}}
}int main(){cin>>n>>m>>k>>t;memset(h,-1,sizeof h);for(int i=1;i<=n;i++){cin>>w[i];}memset(dist,0x3f,sizeof dist);while(m--){int x;cin>>x;dist[x]=0; //初始作物已有,不需要生成,所以生成时间为0st[x]=true;q.push(x);}while(k--){int a,b,c;cin>>a>>b>>c;add(a,b,c); //因为填充dist[a]和dist[b]时都需要知道利用它的杂交方式,所以得是无向边,便于访问 add(b,a,c);}spfa();cout<<dist[t];return 0;
}
三、知识风暴
Spfa算法
- spfa算法为队列优化的Bellman-Ford算法。
- 基本思想:在Bellman-Ford算法基础上,不是每次都进行松弛操作(如果存在边
(a,b,c),即a到b的边且边权为c,而且dist[a]>dist[b]+c(dist[i]存储1号点到i号点的最短路径的长度)即可进行松弛),而是如果一个点被更新过,将它加入队列中,然后利用它来松弛其他点,然后将该点弹出,再将更新过的点加入队列中,循环往复,直到队列为空,算法结束。
相关文章:

【蓝桥杯集训·每日一题】AcWing 3305. 作物杂交
文章目录一、题目1、原题链接2、题目描述二、解题报告1、思路分析2、时间复杂度3、代码详解三、知识风暴Spfa算法一、题目 1、原题链接 3305. 作物杂交 2、题目描述 作物杂交是作物栽培中重要的一步。 已知有 N 种作物 (编号 1 至 N),第 i 种作物从播种到成熟的时间…...

深入浅出PaddlePaddle函数——paddle.to_tensor
分类目录:《深入浅出PaddlePaddle函数》总目录 相关文章: 深入浅出PaddlePaddle函数——paddle.Tensor 深入浅出PaddlePaddle函数——paddle.to_tensor 通过已知的data来创建一个Tensor,Tensor类型为paddle.Tensor。data可以是scalar、tupl…...

JavaScript高级程序设计读书分享之10章——函数
JavaScript高级程序设计(第4版)读书分享笔记记录 适用于刚入门前端的同志 定义函数 定义函数有两种方式:函数声明和函数表达式大致看这两种方式没有什么区别,事实上,JavaScript 引擎在加载数据时对它们是区别对待的。JavaScript 引擎在任何代…...

第八章 使用 ^%ZSTART 和 ^%ZSTOP 例程自定义启动和停止行为 - 设计注意事项
文章目录第八章 使用 ^%ZSTART 和 ^%ZSTOP 例程自定义启动和停止行为 - 设计注意事项设计注意事项第八章 使用 ^%ZSTART 和 ^%ZSTOP 例程自定义启动和停止行为 - 设计注意事项 IRIS 可以在特定事件发生时执行自定义代码。需要两个步骤: 定义 ^%ZSTART 例程、^%ZSTO…...
工作实战之拦截器模式
目录 前言 一、结构中包含的角色 二、拦截器使用 1.拦截器角色 a.自定义拦截器UserValidateInterceptor,UserUpdateInterceptor,UserEditNameInterceptor b.拦截器配置者UserInterceptorChainConfigure,任意组装拦截器顺序 c.拦截器管理者…...
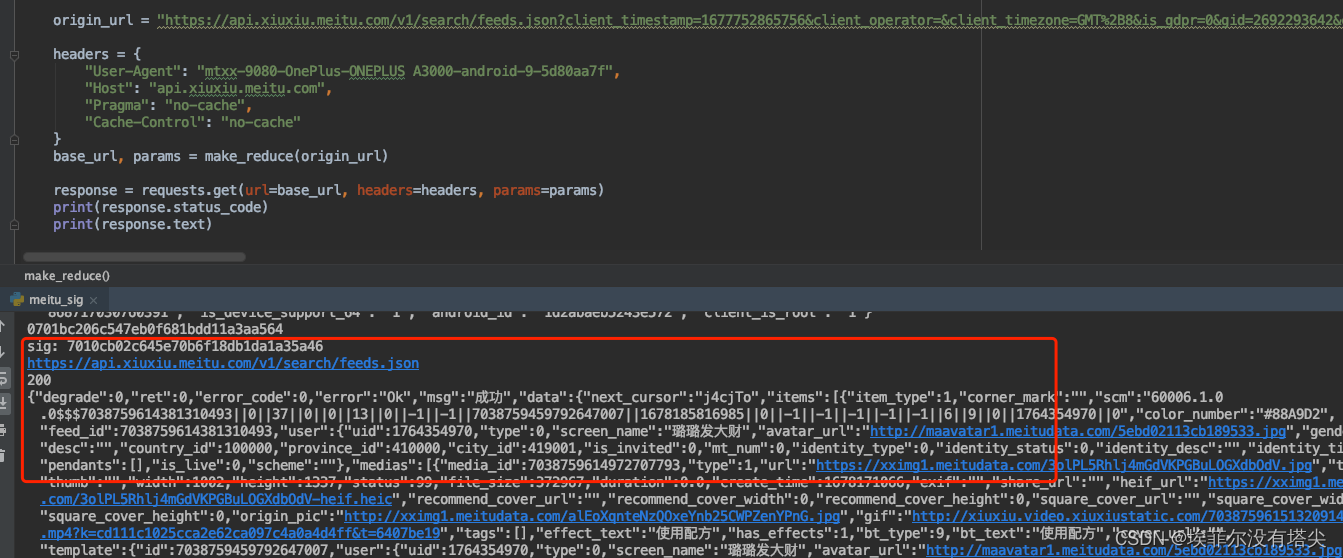
某美颜app sig参数分析
之前转载过该app的文章,今天翻版重新整理下,版本号:576O5Zu56eA56eAYXBwIHY5MDgw (base64 解码)。 上来先抓个包: jadx搜索关键词 "sigTime",然后定位到这里 看这行代码 cVar.addForm(INoCaptchaComponent.sig, genera…...

Linux - Linux系统优化思路
文章目录影响Linux性能的因素CPU内存磁盘I/O性能网络宽带操作系统相关资源系统安装优化内核参数优化文件系统优化应用程序软件资源系统性能分析工具vmstat命令iostat命令sar命令系统性能分析标准小结影响Linux性能的因素 CPU CPU是操作系统稳定运行的根本,CPU的速…...
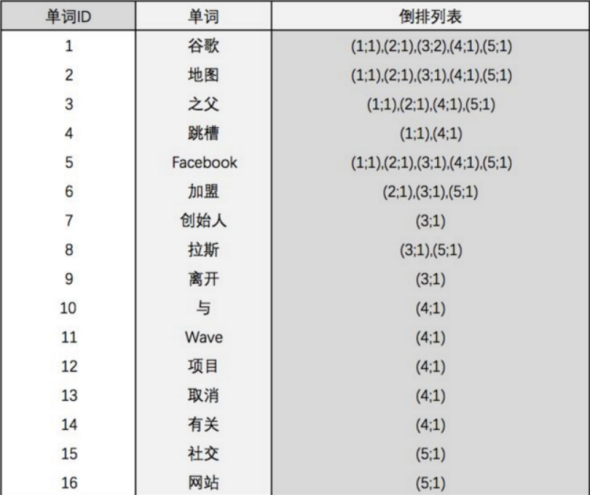
2.Elasticsearch入门
2.Elasticsearch入门[toc]1.Elasticsearch简介Elasticsearch是用Java开发并且是当前最流行的开源的企业级搜索引擎。 能够达到实时搜索,稳定,可靠,快速,安装使用方便。客户端支持Java、.NET(C#)、PHP、Pyth…...
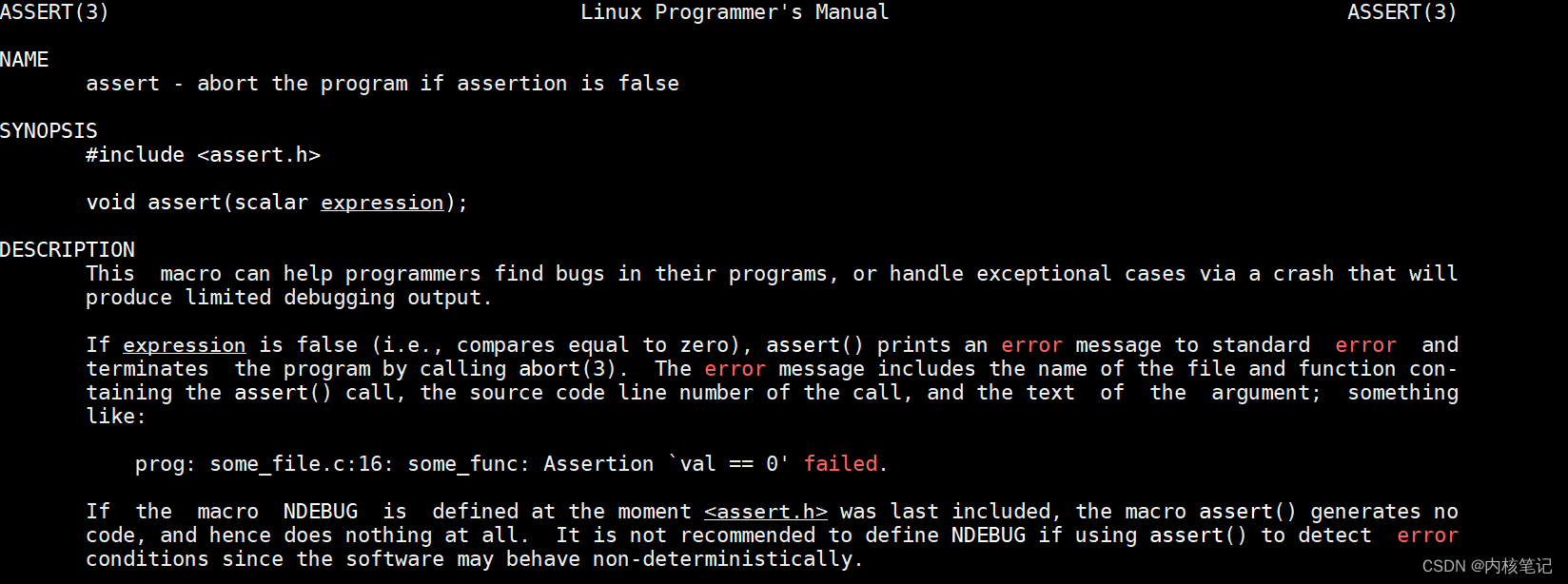
RK3399平台开发系列讲解(应用开发篇)断言的使用
🚀返回专栏总目录 文章目录 一、什么是断言二、静态断言三、运行时断言沉淀、分享、成长,让自己和他人都能有所收获!😄 📢断言为我们提供了一种可以静态或动态地检查程序在目标平台上整体状态的能力,与它相关的接口由头文件 assert.h 提供。 一、什么是断言 在编程中…...
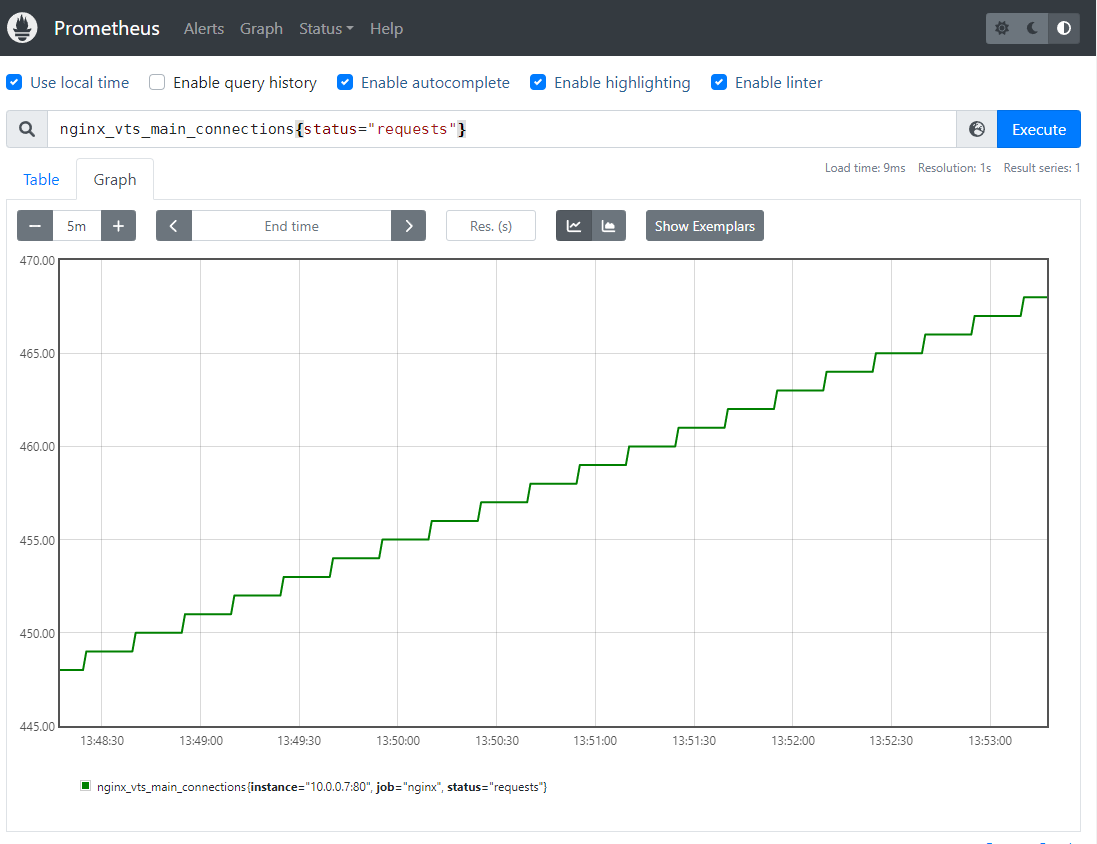
云原生系列之使用prometheus监控nginx
前言 大家好,又见面了,我是沐风晓月,本文主要讲解云原生系列之使用prometheus监控nginx 文章收录到 csdn 我是沐风晓月的博客【prometheus监控系列】专栏,此专栏是沐风晓月对云原生prometheus的的总结,希望能够加深自…...
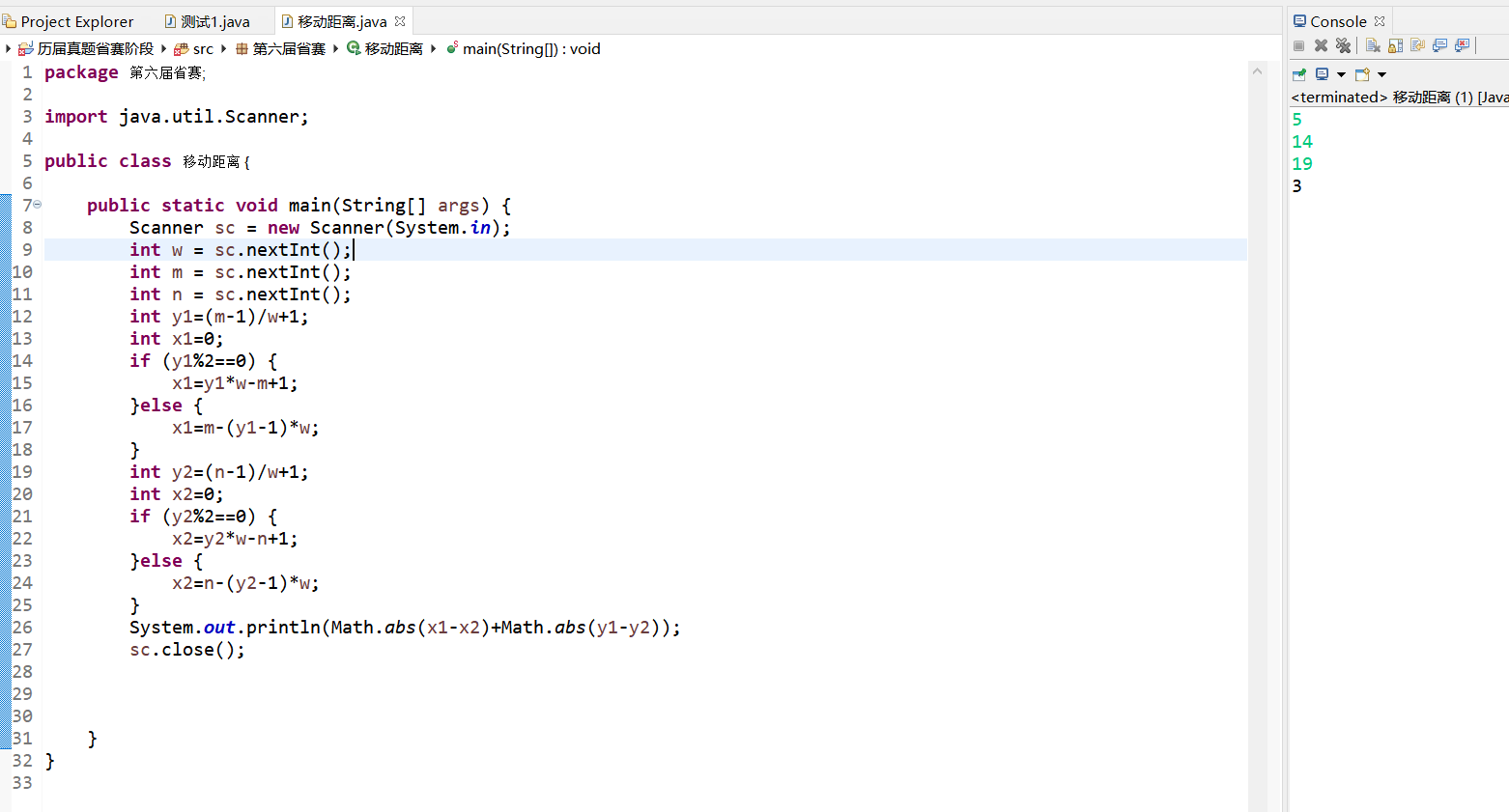
第六届省赛——8移动距离(总结规律)
题目:X星球居民小区的楼房全是一样的,并且按矩阵样式排列。其楼房的编号为1,2,3...当排满一行时,从下一行相邻的楼往反方向排号。比如:当小区排号宽度为6时,开始情形如下:1 2 3 4 5 612 11 10 9 8 713 14 1…...
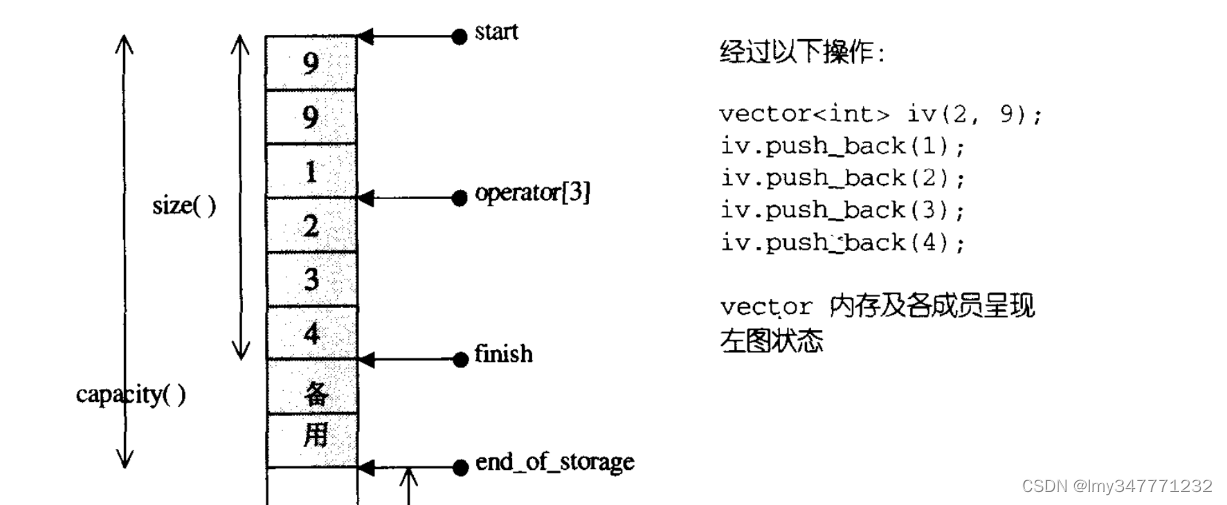
C++vector 简单实现
一。概述 vector是我们经常用的一个容器,其本质是一个线性数组。通过对动态内存的管理,增删改查数据,达到方便使用的目的。 作为一个线性表,控制元素个数,容量,开始位置的指针分别是: start …...
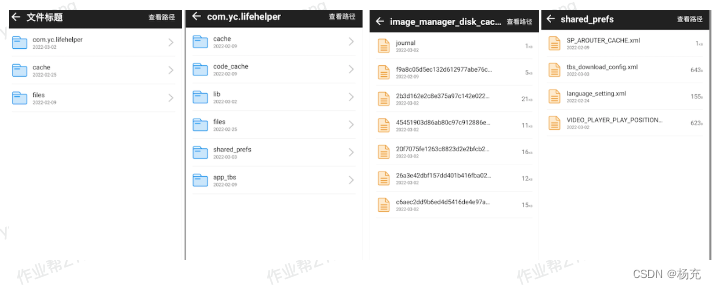
通用缓存存储设计实践
目录介绍 01.整体概述说明 1.1 项目背景介绍1.2 遇到问题记录1.3 基础概念介绍1.4 设计目标1.5 产生收益分析 02.市面存储方案 2.1 缓存存储有哪些2.2 缓存策略有哪些2.3 常见存储方案2.4 市面存储方案说明2.5 存储方案的不足 03.存储方案原理 3.1 Sp存储原理分析3.2 MMKV存储…...

sheng的学习笔记Eureka Ribbon
Eureka-注册中心Eureka简介官方网址:https://spring.io/projects/spring-cloud-netflixEureka介绍Spring Cloud 封装了 Netflix 公司开发的 Eureka 模块来实现服务注册和发现(请对比Zookeeper)。Zooleeper nacos.Eureka 采用了 C-S 的设计架构。Eureka Server 作为服…...
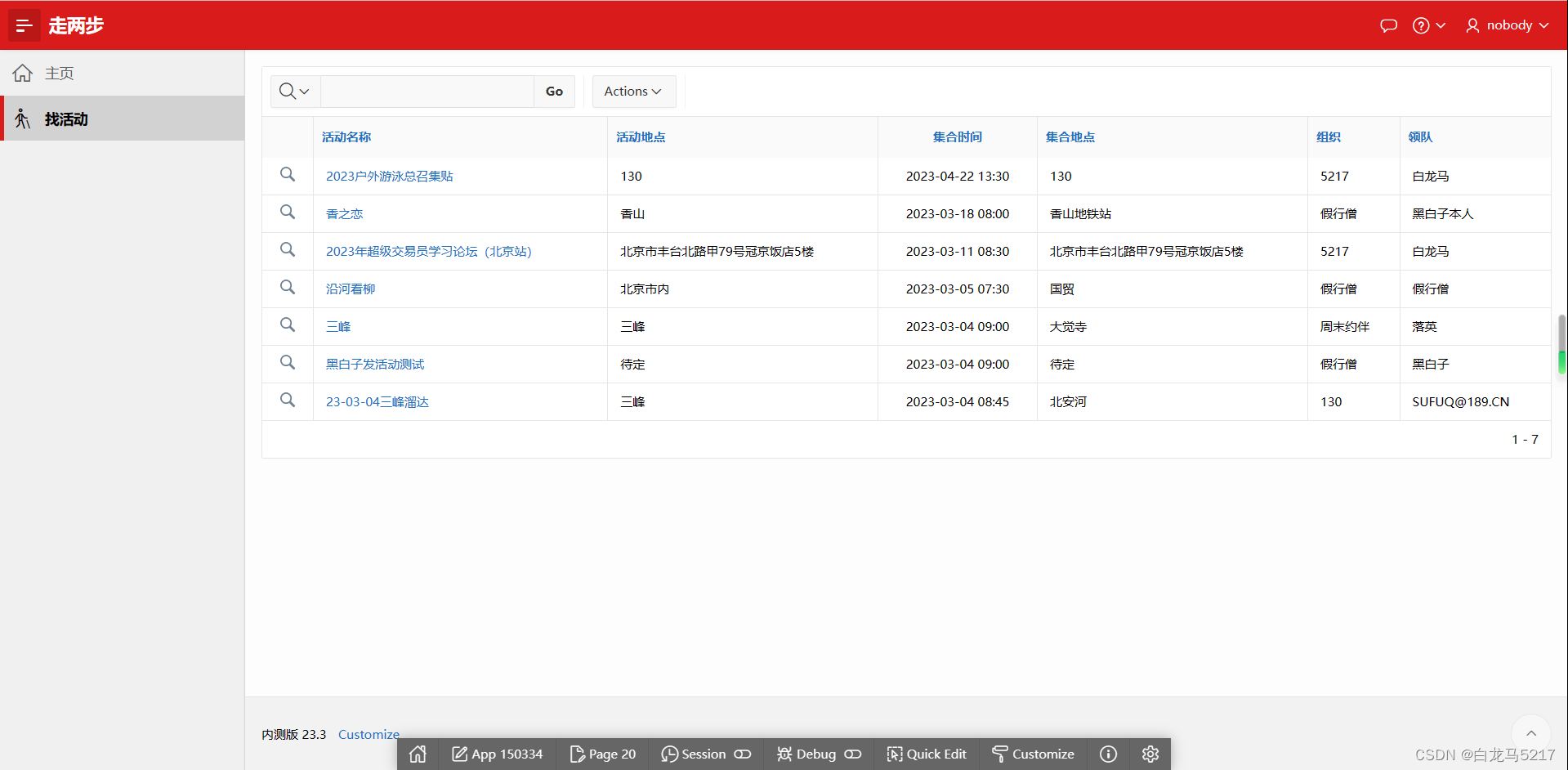
零代码工具我推荐Oracle APEX
云原生时代零代码工具我推荐Oracle APEX 国内的低码开发平台我也看了很多,感觉还是不太适合我这个被WEB抛弃的老炮。自从看了Oracle APEX就不打算看其它的了。太强大了,WEB服务器都省了,直接数据库到WEB页面。功能很强大,震撼到我…...
InstructGPT方法简读
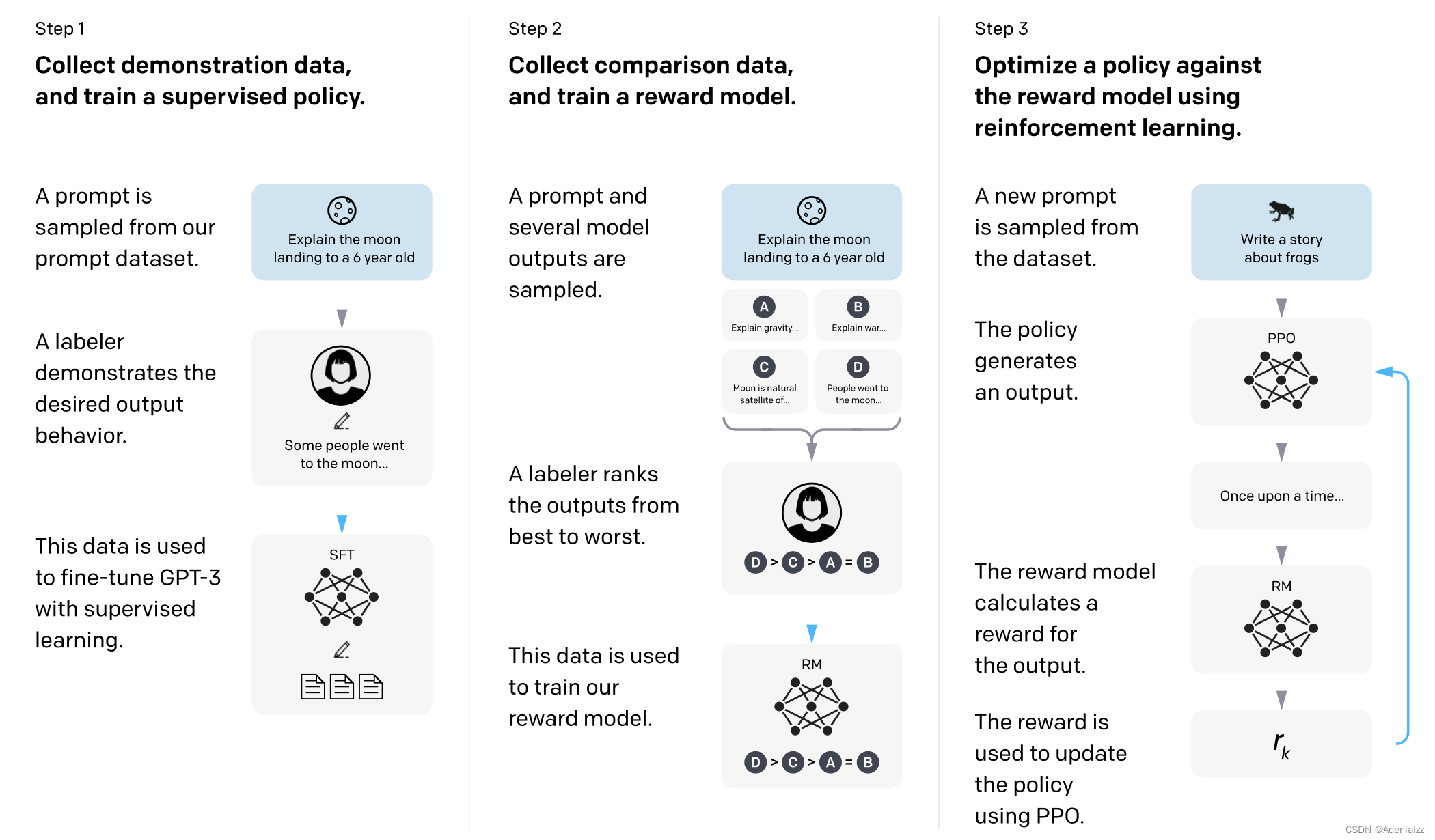
InstructGPT方法简读 引言 仅仅通过增大模型规模和数据规模来训练更大的模型并不能使得大模型更好地理解用户意图。由于数据的噪声极大,并且现在的大多数大型语言模型均为基于深度学习的“黑箱模型”,几乎不具有可解释性和可控性,因此&…...

SpringCloud-5_模块集群化
避免一台Server挂掉,影响整个服务,搭建server集群创建e-commerce-eureka-server-9002微服务模块【作为注册中心】创建步骤参考e-commerce-eureka-server-9001修改pom.xml,加入依赖同9001创建resources/application.yml9002的ymlserver: # 修改端口号por…...
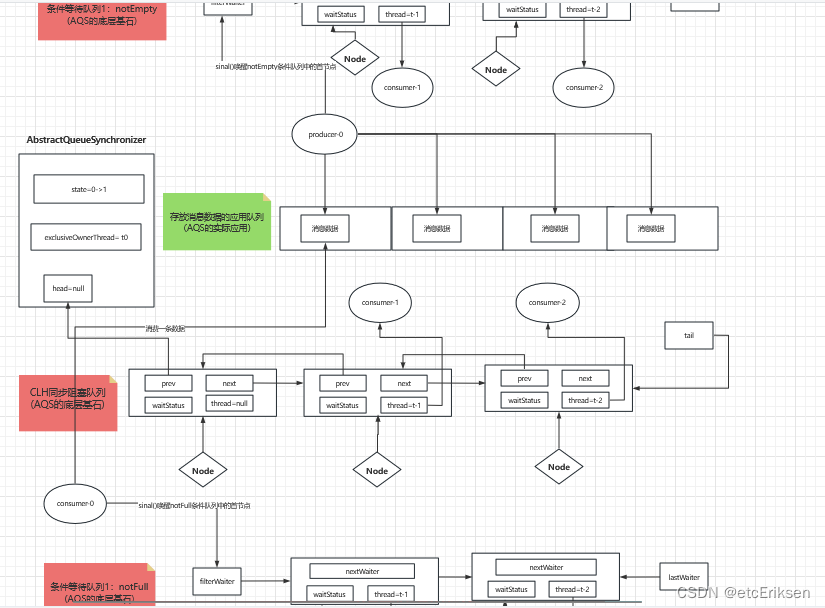
AQS底层源码深度剖析-BlockingQueue
目录 AQS底层源码深度剖析-BlockingQueue BlockingQueue定义 队列类型 队列数据结构 ArrayBlockingQueue LinkedBlockingQueue DelayQueue BlockingQueue API 添加元素 检索(取出)元素 BlockingQueue应用队列总览图 AQS底层源码深度剖析-BlockingQueue【重点中的重…...

Kotlin协程:Flow的异常处理
示例代码如下:launch(Dispatchers.Main) {// 第一部分flow {emit(1)throw NullPointerException("e")}.catch {Log.d("liduo", "onCreate1: $it")}.collect {Log.d("liudo", "onCreate2: $it")}// 第二部分flow …...
qt下ffmpeg录制mp4经验分享,支持音视频(h264、h265,AAC,G711 aLaw, G711muLaw)
前言 MP4,是最常见的国际通用格式,在常见的播放软件中都可以使用和播放,磁盘空间占地小,画质一般清晰,它本身是支持h264、AAC的编码格式,对于其他编码的话,需要进行额外处理。本文提供了ffmpeg录…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...
