计算机视觉之三维重建(5)---双目立体视觉
文章目录
- 一、平行视图
- 1.1 示意图
- 1.2 平行视图的基础矩阵
- 1.3 平行视图的极几何
- 1.4 平行视图的三角测量
- 二、图像校正
- 三、对应点问题
- 3.1 相关匹配法
- 3.2 归一化相关匹配法
- 3.3 窗口问题
- 3.4 相关法存在的问题
- 3.5 约束问题
一、平行视图
1.1 示意图
如下图即是一个平行视图。特点:(1) 两个平面平行。 (2) 基线平行于图像平面,极点 e e e 和 e ′ e' e′ 位于无穷远处。

1.2 平行视图的基础矩阵
1. 对于基础矩阵我们有另一个表达式: F = e ′ × K ′ R K − 1 F=e'×K'RK^{−1} F=e′×K′RK−1,推导过程如下所示。

2. 在平行视图情况下,极点交于无穷远处,所以我们可以假定极点 e ′ = [ 1 , 0 , 0 ] T e'=[1,0,0]^T e′=[1,0,0]T,平行视图下, K = K ′ K=K' K=K′, R = I R=I R=I,那么对于平行视图有:

1.3 平行视图的极几何
1. 极线是水平的,平行于 u u u 轴。
2. 平行视图下, p p p 和 p ′ p' p′ 在 v v v 轴方向坐标相同,即垂直方向没有变换。
3. 极点位于无穷远处。
4. 已知 p p p 和 F F F 的情况下, p ′ p' p′ 只需要按着扫描线寻找即可,扫描线指的是过 p p p 且平行于 u u u 轴的线。


1.4 平行视图的三角测量
1. 俯视这个平行视图,两个摄像机平面就会变成线。 P P P 到 O 1 O_1 O1 和 O 2 O_2 O2 的距离表示为深度 z z z, O 1 O_1 O1 和 O 2 O_2 O2 的距离为 B B B,焦距为 f f f。利用相似三角形底比高可得视差与深度 z z z 成反比。


2. (1) 平行视图中的视差图:根据两台平行摄像机在不同角度观察同一物体或场景时,由于视角差异造成的图像的差异进而推断出物体的深度和距离,得到一幅信息图,可以用于对物体或场景的三维重建和识别。 (2) 3D电影通过用两个摄像头同时模拟拍摄同一场景,模拟人眼双眼视觉,再将两个平行视图分别投影到屏幕上,由于使用特殊的偏振式眼睛,通过人眼的立体视觉原理,会给观众感知到一种立体的深度效果。


二、图像校正
1. 图像校正:使一组非平行视图通过校正构建成平行视图。
2. 图像校正有五步:
(1) 在两幅图像 l l l 和 l ′ l' l′ 上找到一组匹配点 p i ↔ p i ′ p_i↔p'_i pi↔pi′,不少于 8 8 8 个。
(2) 计算基础矩阵 F F F(八点法),求解两幅图像中的极点 e e e 和 e ′ e' e′。

(3) 选择透视变换 H ′ H' H′ 将 e ′ e' e′ 映射到无穷远点 ( f , 0 , 0 ) (f,0,0) (f,0,0),变换公式: H = T − 1 G R T H=T^{-1}GRT H=T−1GRT。
① 先将图像的中心点从左下角移到中心。② 构造 R R R。③ 构造 G G G。

(4) 对透视变换矩阵 H H H 进行变换,使得经过 H H H 和 H ′ H' H′ 变换后的两个像平面满足平行视图要求: Σ d ( H p i , H ′ p i ′ ) Σd(Hp_i,H'p_i') Σd(Hpi,H′pi′)。
(5) 分别利用新的矩阵 H H H 和 H ′ H' H′,对左右两幅图像 l l l 和 l ′ l' l′ 进行重采样,得到一组平行视图。

三、对应点问题
对应点搜索问题,即根据 p p p 点寻找对应 p ′ p' p′ 点的问题,我们根据平行视图极几何关系可知, p ′ p' p′ 点一定在扫描线上,这样可以进一步缩小的检索范围。
3.1 相关匹配法
通过点与点之间 3 ∗ 3 3*3 3∗3 窗口的相关性来进行判断。作为相关性标准,该方法可行依据在于,一般情况下一个图像上像素颜色或灰度的变化是平滑的,这样近似相同点平方的最大值的和在理论上大于高偏差点平方的最大值的和。

3.2 归一化相关匹配法
1. 对于一个图像上存在像素颜色或灰度变化突变的情况,上一种方法会出现计算误差较大,所以需要进行归一化。
2. 归一化相关匹配法:改变原来的相似性度量,通过每个窗口向窗口均值进行归一化,达到平滑的效果。


3.3 窗口问题
对于较小的窗口:会引入更多的噪声,更容易受到噪声影响,但反之也会在没有噪声影响的地方提供更精确的信息。对于较大的窗口:通过归一化操作可以平滑更多的噪声,但也会丢失一部分细节。

3.4 相关法存在的问题
1. 透视缩短和遮挡问题:

2. 当遇到不规则物体在视角上存在遮挡时,可能由于 B / z B/z B/z 的过大,两个像平面无法得到更多的信息交互,导致信息丢失,所以可以适当减小 B / z B/z B/z。但当 B / z B/z B/z 过小时,由于双目视觉上遮挡的信息只能尽量的去弱化,不能去消除,所以当 B / z B/z B/z 过小时,物体的突出部会造成过大的深度误差,从而在三维重建过程中存在视觉上的明显错误。

3. 同质区域:由于存在世界坐标下不同区域但颜色非常相近的地方,所以会导致误差的产生,比如用双目视觉去测量一堵白墙的形状,但光影极其不明显。

4. 对于世界实物上存在重复的区域,这会对双目视觉的三维重建产生较大的影响。

3.5 约束问题
1. 唯一性约束:对于一张图像中的任何点,在另一张图像上最多只有一个匹配点,不存在同质区域和重复区域。

2. 顺序约束/单调性约束:左右视图中的对应点次序一致,保证不存在遮挡。

3. 平滑性约束:视差函数通常是平滑的,减少曝光亮度突变的问题。

相关文章:

计算机视觉之三维重建(5)---双目立体视觉
文章目录 一、平行视图1.1 示意图1.2 平行视图的基础矩阵1.3 平行视图的极几何1.4 平行视图的三角测量 二、图像校正三、对应点问题3.1 相关匹配法3.2 归一化相关匹配法3.3 窗口问题3.4 相关法存在的问题3.5 约束问题 一、平行视图 1.1 示意图 如下图即是一个平行视图。特点&a…...

计算机网络-TCP/IP 网络模型
TCP/IP网络模型各层的详细描述: 应用层:应用层为应用程序提供数据传输的服务,负责各种不同应用之间的协议。主要协议包括: HTTP:超文本传输协议,用于从web服务器传输超文本到本地浏览器的传送协议。FTP&…...

算法训练营第29天|LeetCode 491.递增子序列 46.全排列 47.全排列Ⅱ
LeetCode 491.递增子序列 题目链接: LeetCode 491.递增子序列 解题思路: 用哈希集合进行去重,同一树层不能取重复元素。 代码: class Solution { public:vector<vector<int>>result;vector<int>path;void…...

Ubuntu服务器搭建 - 环境篇
Ubuntu服务器搭建 - 环境篇 基于腾讯云服务器 - Ubuntu 20.04 LTS 一、安装 - MySQL 1.1 概述 MySQL安装方式有三种: 1. 使用Ubuntu 包管理工具 apt安装 2. 使用MySQL官方APT存储库安装 3. 使用MySQL官方二进制发行版安装 1.2 安装 MySQL 使用MySQL官方APT存储库安装 $ wget…...

深度学习基础模型之Mamba
Mamba模型简介 问题:许多亚二次时间架构(运行时间复杂度低于O(n^2),但高于O(n)的情况)(例如线性注意力、门控卷积和循环模型以及结构化状态空间模型(SSM))已被开发出来,以解决 Transformer 在长…...

Topaz Video AI for Mac v5.0.0激活版 视频画质增强软件
Topaz Video AI for Mac是一款功能强大的视频处理软件,专为Mac用户设计,旨在通过人工智能技术为视频编辑和增强提供卓越的功能。这款软件利用先进的算法和深度学习技术,能够自动识别和分析视频中的各个元素,并进行智能修复和增强&…...

解决WordPress文章的段落首行自动空两格的问题
写文章时,段落首行都会空两格,可是WordPress自带的编辑器却没有考虑到这一点,导致发布的文章首行都是顶格的,看起来很不习惯。 我们通常的解决方法都是在发布文章时把编辑器切换到“文本”模式,然后再在首行手动键入两…...

RISC-V单板计算机模拟和FPGA板多核IP实现
🎯要点 🎯使用单板计算机 Visionfive 2 或模拟器测试RISC-V汇编🎯RISC-V汇编加载和算术。🎯使用GNU MAKE汇编RISC-V指令,ESP32使用CMake编译执行指令。🎯RISC-V汇编功能和使用释义:控制指令&am…...

Mojo编程语言案例及介绍
Mojo是一种新兴的编程语言,它结合了现代编程范式与简洁易读的语法,为开发者提供了一个强大且高效的开发工具。以下将详细介绍Mojo编程语言的特性,并通过一个实际案例来展示Mojo的应用。 一、Mojo编程语言介绍 Mojo编程语言的设计理念是“简单…...
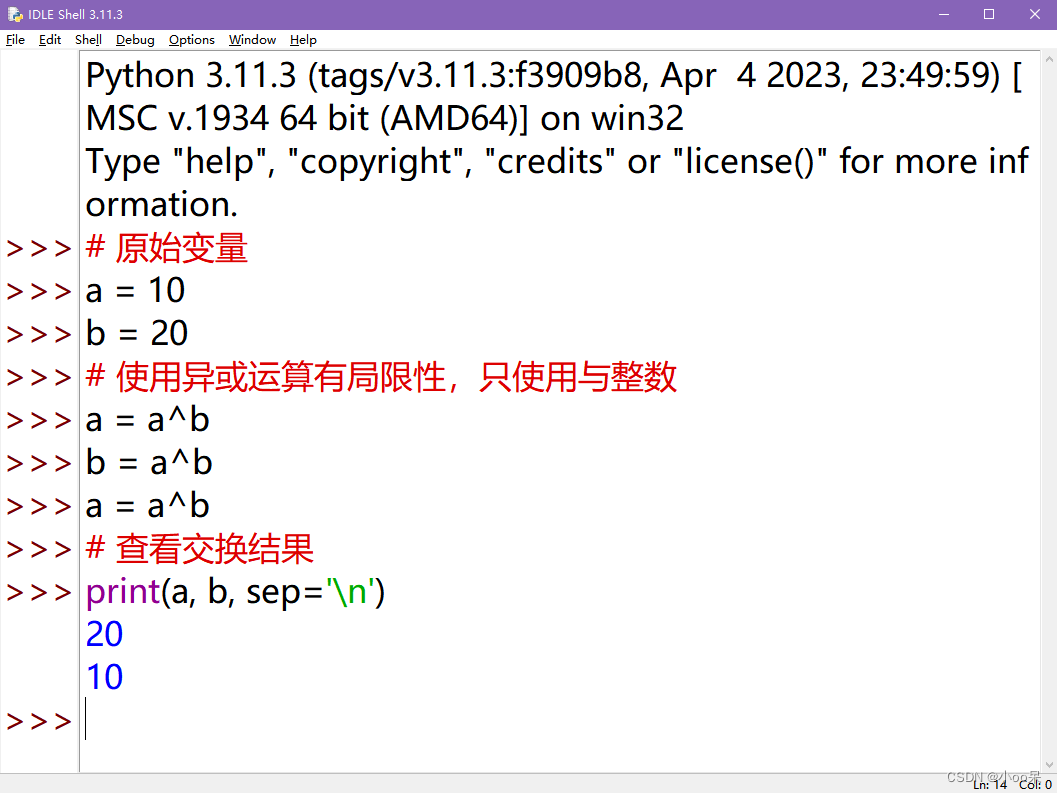
【Python面试题收录】Python中有哪些方法交换两个变量的值?至少给出三种方法。
一、使用临时变量 # 定义原始变量 a 10 b 20# 直接交换,Python会一次性执行两个赋值操作 a, b b, a# 无需额外变量,a 和 b 的值已经交换 print(a) # 输出: 20 print(b) # 输出: 10 二、利用元组解包特性(不使用临时变量,推荐…...

MySQL核心命令详解与实战,一文掌握MySQL使用
文章目录 文章简介演示库表创建数据库表选择数据库删除数据库创建表删除表向表中插入数据更新数据删除数据查询数据WHERE 操作符聚合函数LIKE 子句分组 GROUP BY HAVINGORDER BY(排序) 语句LIMIT 操作符 分页查询多表查询-联合查询 UNION 操作符多表查询-连接的使用-JOIN语句编…...
基于Springboot + MySQL + Vue 大学新生宿舍管理系统 (含源码)
目录 📚 前言 📑摘要 📑操作流程 📚 系统架构设计 📚 数据库设计 💬 管理员信息属性 💬 学生信息实体属性 💬 宿舍安排信息实体属性 💬 卫生检查信息实体属性 &…...
vulnhub pWnOS v2.0通关
知识点总结: 1.通过模块来寻找漏洞 2.msf查找漏洞 3.通过网站源代码,查看模块信息 环境准备 攻击机:kali2023 靶机:pWnOS v2.0 安装地址:pWnOS: 2.0 (Pre-Release) ~ VulnHub 在安装网址中看到,该靶…...

leetcode热题100.数据流的中位数
作者:晓宜 🌈🌈🌈 个人简介:互联网大厂Java准入职,阿里云专家博主,csdn后端优质创作者,算法爱好者 ❤️❤️❤️ 你的关注是我前进的动力😊 Problem: 295. 数据流的中位数…...

C 从函数返回指针
我们已经了解了 C 语言中如何从函数返回数组,类似地,C 允许您从函数返回指针。为了做到这点,您必须声明一个返回指针的函数,如下所示: int * myFunction() { . . . }另外,C 语言不支持在调用函数时返回局部…...
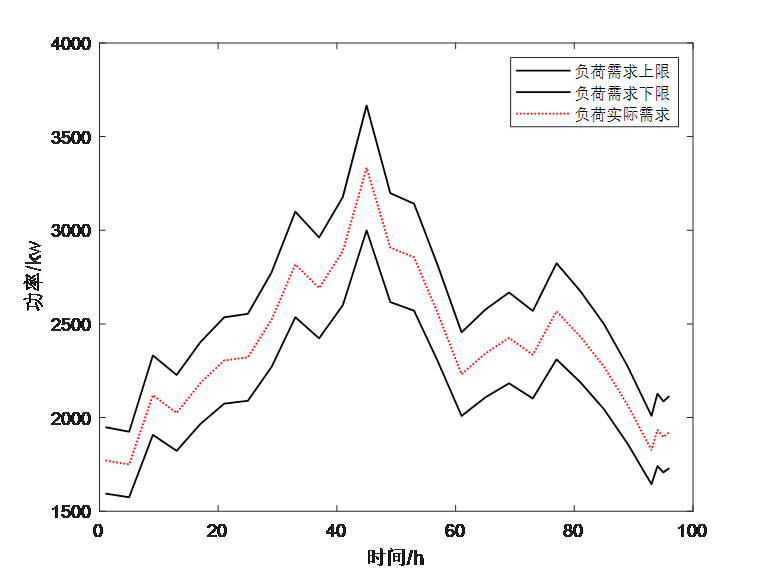
(文章复现)考虑分布式电源不确定性的配电网鲁棒动态重构
参考文献: [1]徐俊俊,吴在军,周力,等.考虑分布式电源不确定性的配电网鲁棒动态重构[J].中国电机工程学报,2018,38(16):4715-47254976. 1.摘要 间歇性分布式电源并网使得配电网网络重构过程需要考虑更多的不确定因素。在利用仿射数对分布式电源出力的不确定性进行合…...

蓝桥杯第八届c++大学B组详解
目录 1.购物单 2.等差素数列 3.承压计算 4.方格分割 5.日期问题 6.包子凑数 7.全球变暖 8.k倍区间 1.购物单 题目解析:就是将折扣字符串转化为数字,进行相加求和。 #include<iostream> #include<string> #include<cmath> usin…...

小于n的最大数 Leetcode 902 Numbers At Most N Given Digit Set
这两个问题的本质就是一个棵树,然后根据n对树做剪枝。难点在于剪的时候边界条件有些坑,get_lower_largest_digit_dic是这两个题目的共同点 题目一: 小于n的最大数 算法题目:小于n的最大数 问题描述:给一个数组nums[5…...

Leetcode刷题-数组(二分法、双指针法、窗口滑动)
数组 1、二分法 704. 二分查找 - 力扣(LeetCode) 需要注意区间的问题。首先在最外面的循环判断条件是left<right。那就说明我们区间规定的范围就是【left,right】 属于是左闭右闭!!!!!&…...

STM32学习和实践笔记(4): 分析和理解GPIO_InitTypeDef GPIO_InitStructure (b)
继续上篇博文:STM32学习和实践笔记(4): 分析和理解GPIO_InitTypeDef GPIO_InitStructure (a)-CSDN博客 往下写, 为什么:当GPIO_InitStructure.GPIO_PinGPIO_Pin_0 ; 时,其实就是将对应的该引脚的寄存器地…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...
