回溯算法|78.子集
力扣题目链接
class Solution {
private:vector<vector<int>> result;vector<int> path;void backtracking(vector<int>& nums, int startIndex) {result.push_back(path); // 收集子集,要放在终止添加的上面,否则会漏掉自己if (startIndex >= nums.size()) { // 终止条件可以不加return;}for (int i = startIndex; i < nums.size(); i++) {path.push_back(nums[i]);backtracking(nums, i + 1);path.pop_back();}}
public:vector<vector<int>> subsets(vector<int>& nums) {result.clear();path.clear();backtracking(nums, 0);return result;}
};
这题比较好理解啦~
思路
求子集问题和77.组合 (opens new window)和131.分割回文串 (opens new window)又不一样了。
如果把 子集问题、组合问题、分割问题都抽象为一棵树的话,那么组合问题和分割问题都是收集树的叶子节点,而子集问题是找树的所有节点!
其实子集也是一种组合问题,因为它的集合是无序的,子集{1,2} 和 子集{2,1}是一样的。
那么既然是无序,取过的元素不会重复取,写回溯算法的时候,for就要从startIndex开始,而不是从0开始!
有同学问了,什么时候for可以从0开始呢?
求排列问题的时候,就要从0开始,因为集合是有序的,{1, 2} 和{2, 1}是两个集合,排列问题我们后续的文章就会讲到的。
以示例中nums = [1,2,3]为例把求子集抽象为树型结构,如下:
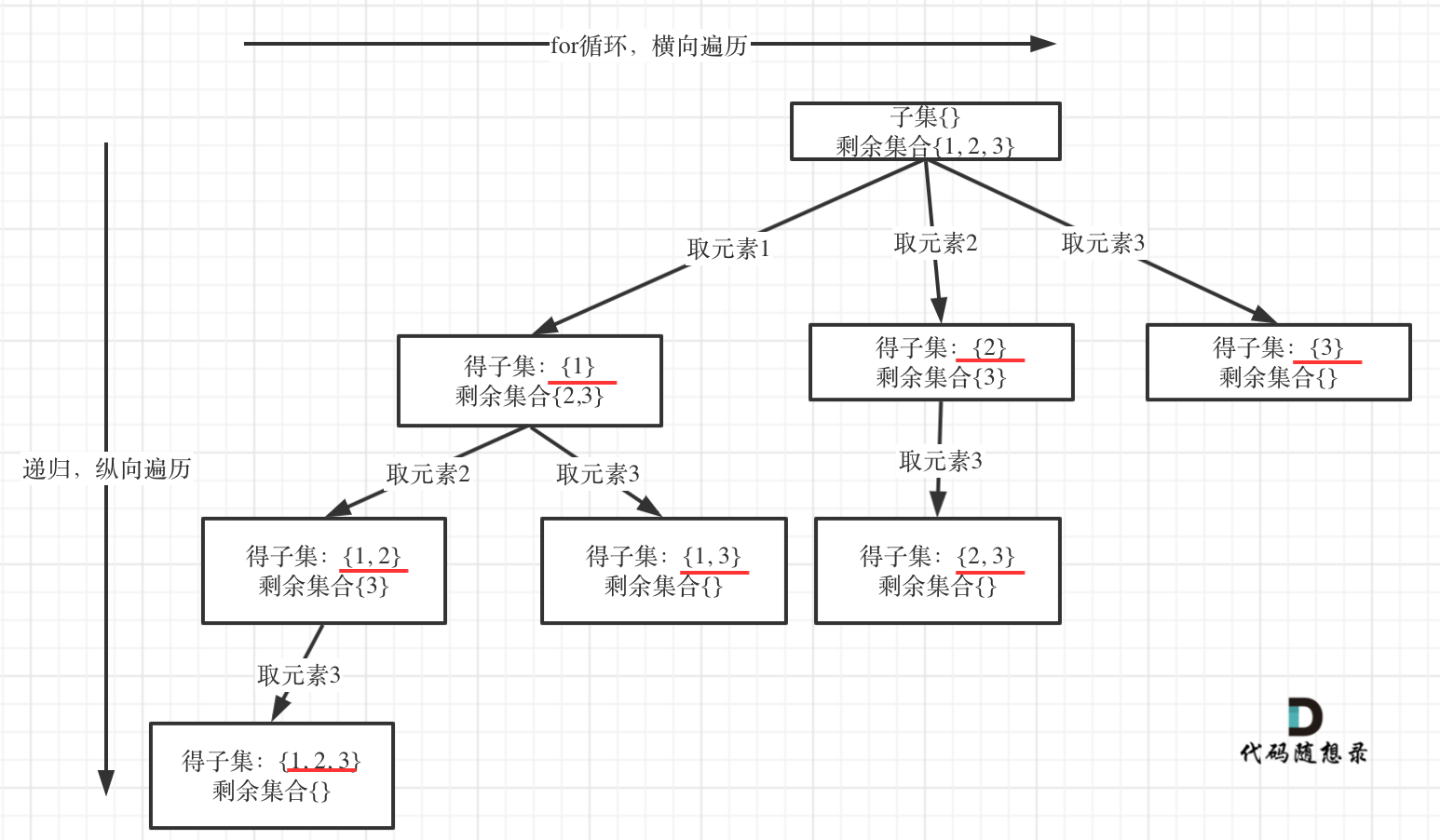
从图中红线部分,可以看出遍历这个树的时候,把所有节点都记录下来,就是要求的子集集合。
#回溯三部曲
- 递归函数参数
全局变量数组path为子集收集元素,二维数组result存放子集组合。(也可以放到递归函数参数里)
递归函数参数在上面讲到了,需要startIndex。
代码如下:
vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int>& nums, int startIndex) {
递归终止条件
从图中可以看出:
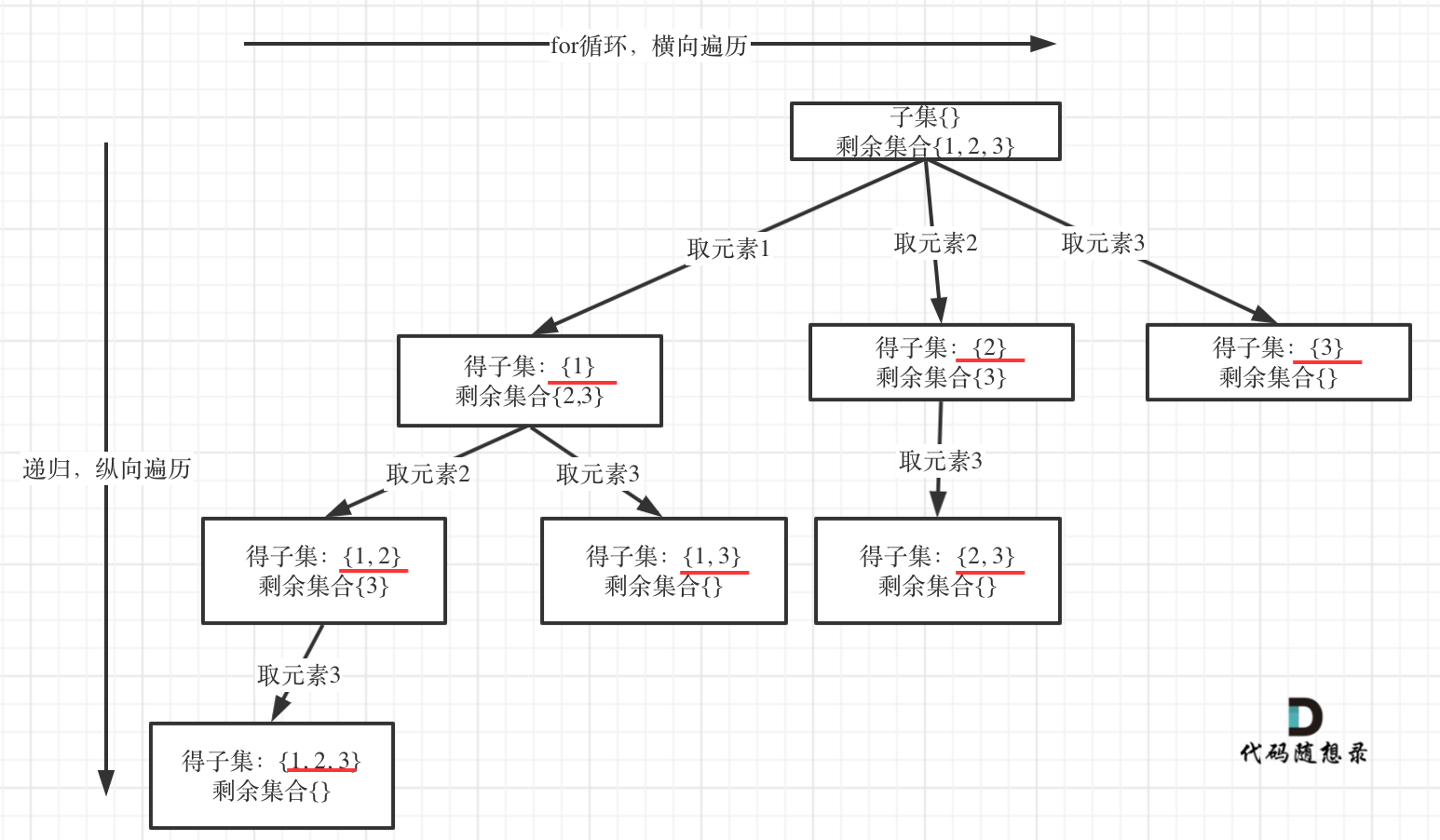
剩余集合为空的时候,就是叶子节点。
那么什么时候剩余集合为空呢?
就是startIndex已经大于数组的长度了,就终止了,因为没有元素可取了,代码如下:
if (startIndex >= nums.size()) {return;
}
其实可以不需要加终止条件,因为startIndex >= nums.size(),本层for循环本来也结束了。
- 单层搜索逻辑
求取子集问题,不需要任何剪枝!因为子集就是要遍历整棵树。
那么单层递归逻辑代码如下:
for (int i = startIndex; i < nums.size(); i++) {path.push_back(nums[i]); // 子集收集元素backtracking(nums, i + 1); // 注意从i+1开始,元素不重复取path.pop_back(); // 回溯
}
根据关于回溯算法,你该了解这些! (opens new window)给出的回溯算法模板:
void backtracking(参数) {if (终止条件) {存放结果;return;}for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {处理节点;backtracking(路径,选择列表); // 递归回溯,撤销处理结果}
}自己的思路:
其实我不太清楚空集它是如何保存的。
result.push_back(path); // 收集子集,要放在终止添加的上面,否则会漏掉自己是这个吗?好像不是
好像也是的,一开始没有路径,直接push进去的就是空集
后面的就和之前几天写的代码差不多了,好理解~

相关文章:

回溯算法|78.子集
力扣题目链接 class Solution { private:vector<vector<int>> result;vector<int> path;void backtracking(vector<int>& nums, int startIndex) {result.push_back(path); // 收集子集,要放在终止添加的上面,否则会漏掉自…...

VC++、GCC、CLANG,INT128有符号整数编译器关键字
注意INT128为目标平台扩展关键字,不属于C/C语言本身支持特性,每个C/C编译器平台支持上都略有不同,甚至不支持。 可以详细参考本人此篇文章: GUN C/C (GCC/CLANG) 对于 __int128_t (128位有符号大整数的扩展支持平台限…...
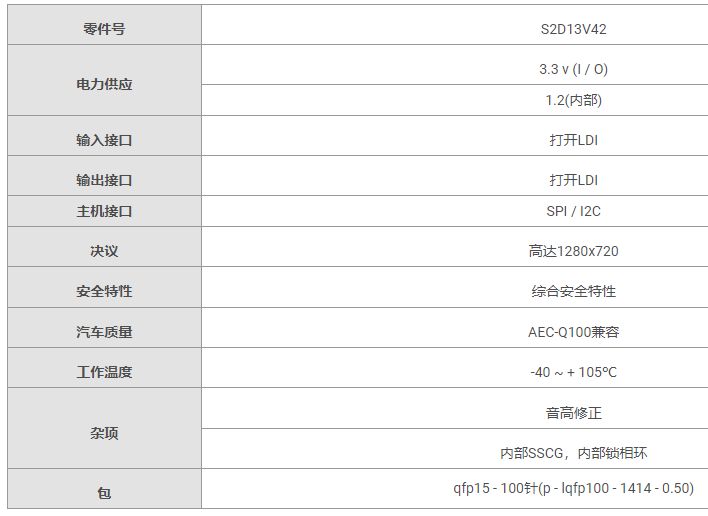
用于HUD平视显示器的控制芯片:S2D13V40
一款利用汽车抬头显示技术用于HUD平视显示器的控制芯片:S2D13V40。HUD的全称是Head Up Display,即平视显示器,以前应用于军用飞机上,旨在降低飞行员需要低头查看仪表的频率。起初,HUD通过光学原理,将驾驶相关的信息投射…...

JSP使用模板字符串数据不能渲染的问题
entrap father 的 rubbish JSP 数据不能直接渲染,要从接口请求后去拼接结构 然后模板字符串不能直接用 用以下方法是不能渲染出数据的 let div <div class"circulation"><div class"list"><div class"left"><div class&qu…...

AI音乐GPT时刻来临:Suno 快速入门手册!
✨✨ 欢迎大家来访Srlua的博文(づ ̄3 ̄)づ╭❤~✨✨ 🌟🌟 欢迎各位亲爱的读者,感谢你们抽出宝贵的时间来阅读我的文章。 我是Srlua小谢,在这里我会分享我的知识和经验。&am…...

数字乡村发展蓝图:科技赋能农村实现全面振兴
目录 一、数字乡村发展蓝图的内涵与目标 二、科技赋能农村:数字乡村发展的动力与路径 (一)加强农业科技创新,提升农业生产效率 (二)推进农村电商发展,拓宽农民增收渠道 (三&…...

Day42 动态规划 part04
Day42 动态规划 part04 46. 携带研究材料(卡哥的卡码网的题目) 背包问题 我的思路: 写不了一点儿…T^T 总结规律就是,dp数组要比原来各个size 1,dp[i][j] Math.max(xxx, xxxx(根据题目情况进行各种处理)) 解答: …...

python set是什么类型
python set是一种数据类型,数学里的集合概念,在Python语言里对应的是set类型。与list,tuple不同的地方是,set更加强调的是一种“从属关系”(membership),跟顺序无关,所以有重复的元素…...
redis事务(redis features)
redis支持事务,也就是可以在一次请求中执行多个命令。redis中的事务主要是通过MULTI和EXEC这两个命令来实现的。 MULTI命令用来开启一个事务,事务开启之后,所有的命令就都会被放入到一个队列中,最后通过一个EXEC命令来执行事务中…...

SpringBoot整合minio
SpringBoot整合minio 1. 下载及安装1.1 windows版本1.2 Linux版本 2. SpringBoot整合minio2.1 依赖2.2 配置文件2.3 配置类2.4 工具类2.5 测试1. 业务层2. 控制层 1. 下载及安装 1.1 windows版本 目录结构 启动文件 标红的地方按实际安装地更改 echo off REM 声明采用UT…...

3090. 每个字符最多出现两次的最长子字符串
说在前面 🎈不知道大家对于算法的学习是一个怎样的心态呢?为了面试还是因为兴趣?不管是出于什么原因,算法学习需要持续保持。 题目描述 给你一个字符串 s ,请找出满足每个字符最多出现两次的最长子字符串,…...

26.活锁、饥饿锁
两个线程,相互改变了对方结束条件,导致两个线程不能结束。执行时间也都是一样,导致两个线程永远不会结束。 Slf4j public class LiveLockDemo {static volatile int count 10;public static void main(String[] args) {new Thread(() ->…...

docker 安装nginx
一、先查看有没有nginx镜像 docker images 二、发现没有nginx镜像,下载最新镜像 docker pull nginx 三、运行镜像 为了先复制出部分文件,先启动一个临时容器 docker run --name nginx -p 9001:80 -d nginx docker cp nginx:/etc/nginx/conf.d /home/…...

2024年阿里云新用户便宜购买云服务器攻略:5大细节助你降低购买成本
随着互联网的蓬勃发展,无论是个人还是企业,拥有一个稳定且高效的网站或APP已成为提升竞争力的关键。为了将这些项目部署并运行起来,购买一台实用又便宜的云服务器是必不可少的。阿里云作为国内首屈一指的云服务提供商,自然成为了众…...

SSTI模板注入(jinja2)
前面学习了SSTI中的smarty类型,今天学习了Jinja2,两种类型都是flask框架的,但是在注入的语法上还是有不同 SSTI:服务器端模板注入,也属于一种注入类型。与sql注入类似,也是通过凭借进行命令的执行ÿ…...

ESP32学习---ESP-NOW(一)
ESP32学习---ESP-NOW(一) 官网简介arduino 官网简介 首先看官网的介绍:https://www.espressif.com.cn/zh-hans/solutions/low-power-solutions/esp-now ESP-NOW 是乐鑫定义的一种无线通信协议,能够在无路由器的情况下直接、快速…...

C++核心高级编程 --- 3、函数提高
文章目录 第三章:3.函数提高3.1 函数默认参数3.2 函数占位参数3.3 函数重载3.3.1 函数重载概述3.3.2 注意事项 第三章: 3.函数提高 3.1 函数默认参数 语法结构:返回值类型 函数名 (参数 默认值){} #include <iostream> using name…...

【微服务篇】深入理解分布式消息队列系统
分布式消息队列是一种在多个服务器、应用或服务之间进行消息传递的技术。它使得各个独立的组件可以通过异步消息进行通信,提高了系统的可扩展性、解耦性和可靠性。 典型应用场景 1. 异步处理 在许多系统中,某些任务的处理可能需要较长时间,…...
基于k8s的web服务器构建
文章目录 k8s综合项目1、项目规划图2、项目描述3、项目环境4、前期准备4.1、环境准备4.2、ip划分4.3、静态配置ip地址4.4、修改主机名4.5、部署k8s集群4.5.1、关闭防火墙和selinux4.5.2、升级系统4.5.3、每台主机都配置hosts文件,相互之间通过主机名互相访问4.5.4、…...

【名词解释】ImageCaption任务中的CIDEr、n-gram、TF-IDF、BLEU、METEOR、ROUGE 分别是什么?它们是怎样计算的?
CIDEr CIDEr(Consensus-based Image Description Evaluation)是一种用于自动评估图像描述(image captioning)任务性能的指标。它主要通过计算生成的描述与一组参考描述之间的相似性来评估图像描述的质量。CIDEr的独特之处在于它考…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...

SQL注入篇-sqlmap的配置和使用
在之前的皮卡丘靶场第五期SQL注入的内容中我们谈到了sqlmap,但是由于很多朋友看不了解命令行格式,所以是纯手动获取数据库信息的 接下来我们就用sqlmap来进行皮卡丘靶场的sql注入学习,链接:https://wwhc.lanzoue.com/ifJY32ybh6vc…...
