Educational Codeforces Round 133 (Rated for Div. 2) (C dp D前缀和优化倍数关系dp)
A:能用3肯定用三,然后分类讨论即可
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5+10,M=2*N,mod=998244353;
#define int long long
typedef long long LL;
typedef pair<int, int> PII;
typedef unsigned long long ULL;
using node=tuple<int,int,int>;
const long long inf=1e18;int n,m,k;
int a[N];void solve()
{cin>>n;if(n==1) cout<<"2\n";else{if(n%3==0) cout<<n/3<<"\n";if(n%3==1) cout<<(n-4)/3+2<<"\n";if(n%3==2) cout<<n/3+1<<"\n";}
}
//1 2 3 4
signed main()
{cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int t=1;cin>>t;while(t--) solve();
}==0==B:
我们可以构造n个
分别是
n n-2 n-3... 0
因为一开始交换会改变两个,然后后面全都和第一个换就可以保证递减下去了
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5+10,M=2*N,mod=998244353;
#define int long long
typedef long long LL;
typedef pair<int, int> PII;
typedef unsigned long long ULL;
using node=tuple<int,int,int>;
const long long inf=1e18;int n,m,k;
int a[N];void solve()
{cin>>n;cout<<1+n-1<<"\n";for(int i=1;i<=n;i++) a[i]=i;//1 2 3 4 4//2 1 3 4 2for(int i=1;i<=n;i++){cout<<a[i]<<" \n"[i==n];}swap(a[1],a[2]);for(int i=2;i<=n;i++){for(int j=1;j<=n;j++){cout<<a[j]<<" \n"[j==n];}swap(a[i+1],a[1]);}
}
//1 2 3 4
signed main()
{cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int t=1;cin>>t;while(t--) solve();
}C:正常都能想到先蛇形再走U字形
dp预处理当前[i,j]走到[i^1,j]的最长等待时间,然后从当前这个时间可以一路往后走,不停下来,
对于同行的dp=max(dp[i][j]+1,a[i][j])
但是对于新增的[i^1,j]也可能造成时间问题
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5+10,M=2*N,mod=998244353;
#define int long long
typedef long long LL;
typedef pair<int, int> PII;
typedef unsigned long long ULL;
using node=tuple<int,int,int>;
const long long inf=1e18;int n,m,k;
int a[3][N];void solve()
{cin>>m;n=2;vector<vector<int>> dp(m + 1, vector<int>(2));for(int i=0;i<n;i++){for(int j=0;j<m;j++)cin>>a[i][j];}a[0][m]=a[1][m]=0;a[0][0]=-1;for(int i=m-1;i>=0;i--){for(int j=0;j<2;j++)dp[i][j]=max({a[j][i]+1,dp[i+1][j]-1,a[j^1][i]-2*(m-i-1)});}int res=inf;array<int,2> pos={0,0};int cur=0;for(int i=0;i<m;i++){res=min(res,max(cur,dp[pos[1]][pos[0]])+2*(m-i)-1);pos[0]^=1;cur=max(a[pos[0]][pos[1]]+1,cur+1);pos[1]++;res=min(res,max(cur,dp[pos[1]][pos[0]])+2*(m-i-1));cur=max(a[pos[0]][pos[1]]+1,cur+1);}cout<<res<<"\n";}
//1 2 3 4
signed main()
{cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int t=1;cin>>t;while(t--) solve();
}D:
因为 (k+1)*(k)/2<=n,可以推出m等于根号2*n
然后直接前缀和优化dp的倍数和即可
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5+10,M=2*N,mod=998244353;typedef long long LL;
typedef pair<int, int> PII;
typedef unsigned long long ULL;
using node=tuple<int,int,int>;
const long long inf=1e18;int n,m,k;
int a[N];
LL res[N];
LL f[2][N],s[N];
void solve()
{cin>>n>>k;f[0][0]=1;m=sqrt(2*n);m++;for(int i=1;i<=m;i++){for(int j=0;j<=n;j++){if(j>=(k+i-1))s[j]=(s[j-(k+i-1)]+f[(i-1)&1][j])%mod;else s[j]=f[(i-1)&1][j]; if(j>=(k+i-1)){f[i&1][j]=(f[i&1][j]+s[j-(k+i-1)])%mod;}}for(int j=0;j<=n;j++){f[(i-1)&1][j]=0;res[j]=(res[j]+f[i&1][j])%mod;}}//(x+1)*(x)/2>=n//x*x>=2*n//max 根号2*n=500for(int i=1;i<=n;i++)cout<<res[i]<<" ";
}
//1 2 3 4
signed main()
{cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int t=1;// cin>>t;while(t--) solve();
}相关文章:
 (C dp D前缀和优化倍数关系dp))
Educational Codeforces Round 133 (Rated for Div. 2) (C dp D前缀和优化倍数关系dp)
A:能用3肯定用三,然后分类讨论即可 #include<bits/stdc.h> using namespace std; const int N 2e510,M2*N,mod998244353; #define int long long typedef long long LL; typedef pair<int, int> PII; typedef unsigned long long ULL; usi…...

【讲解下如何Stable Diffusion本地部署】
🎥博主:程序员不想YY啊 💫CSDN优质创作者,CSDN实力新星,CSDN博客专家 🤗点赞🎈收藏⭐再看💫养成习惯 ✨希望本文对您有所裨益,如有不足之处,欢迎在评论区提出…...
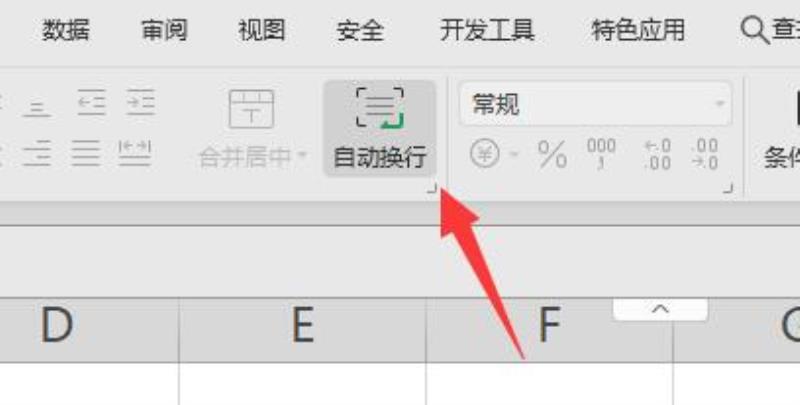
wps斜线表头并分别打字教程
wps斜线表头怎么做并分别打字: 1、首先选中我们想要设置的表头。 2、接着右键选中它,点击“设置单元格格式” 3、然后点击上方“边框”选项卡。 4、随后选择图示的斜线,点击“确定” 5、设置完成后,我们只要在其中打字就可以在斜…...

2024第八届全国青少年无人机大赛暨中国航空航天科普展览会
2024第八届全国青少年无人机大赛暨中国航空航天科普展览会 邀请函 主办单位: 中国航空学会 重庆市南岸区人民政府 招商执行单位: 重庆港华展览有限公司 为更好的培养空航天产业人才,汇聚航空教育产业创新科技,丰富和完善航…...

fastadmin学习08-查询数据渲染到前端
index.php查询,这个是前台的index.php public function index() {$slideImgs Db::name("slideimg")->where("status",,normal)->limit(5)->order(sort,desc)->select();$productList Db::name("product")->where(…...

实验报告答案
基本任务(必做) 先用普通用户(自己的姓名拼音)登录再操作 编程有代码截图和执行过程结果截图 代写获取: https://laowangall.oss-cn-beijing.aliyuncs.com/studentall.pdf 1. Linux的Shell编程 (1&am…...

PDF编辑和格式转换工具 Cisdem PDFMaster for Mac
Cisdem PDFMaster for Mac是一款功能强大的PDF编辑和格式转换工具。它为用户提供了直观且易于使用的界面,使常用功能触手可及,从而帮助用户轻松管理、编辑和转换PDF文件。 软件下载:Cisdem PDFMaster for Mac v6.0.0激活版下载 作为一款完整的…...

E-魔法猫咪(遇到过的题,做个笔记)
题解: 来自学长们思路: 其中一种正解是写单调队列。限制队列内的数单调递增,方法为每当新来的数据比当前队尾数据小时队 尾出列,直到能够插入当前值,这保证了队头永远是最小值。因此总体思路是队尾不断插入新值的同时 …...
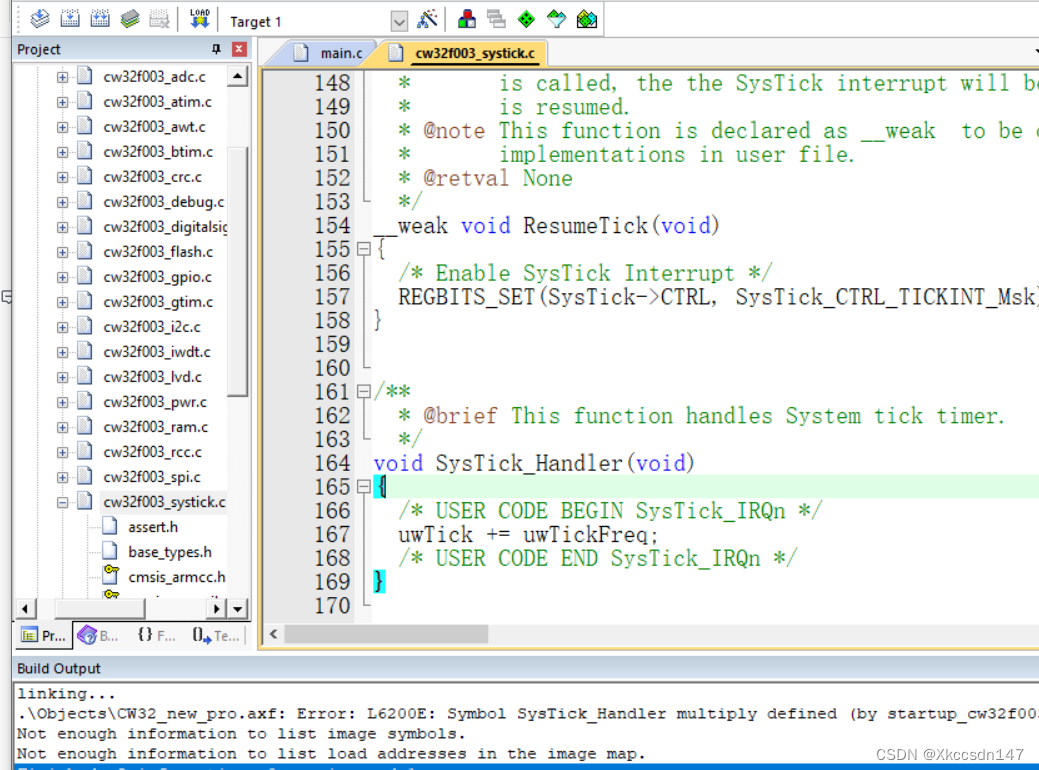
keil创建工程 芯源半导体CW32F003E4P7
提前下载keil 安装步骤 1、下载CW32F003固件库 芯源半导体官网下载固件库 下载好后右键解压 CW32F003_StandardPeripheralLib_V1.5\IdeSupport\MDK 进入MDK文件夹 双击WHXY.CW32F003_DFP.1.0.4.pack安装固件库 点击next然后finish安装结束 keil创建工程 点击new uVision P…...
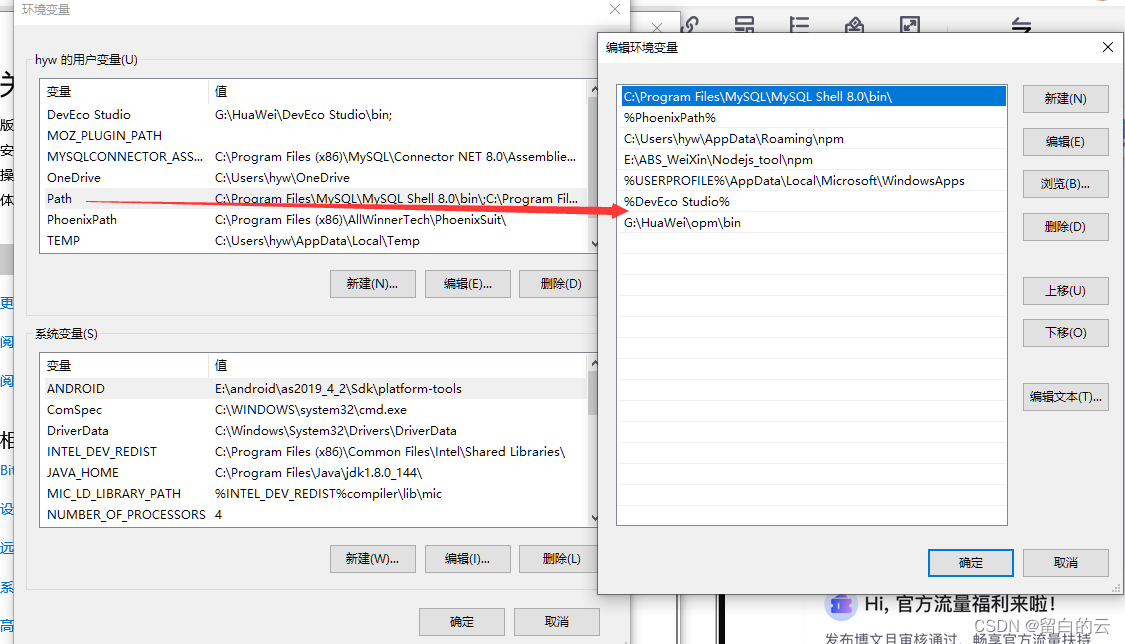
学习鸿蒙基础(12)
目录 一、网络json-server配置 (1)然后输入: (2)显示下载成功。但是输入json-server -v的时候。报错。 (3)此时卸载默认的json-server (4)安装和nodejs匹配版本的js…...

HTML5和CSS3笔记
一:网页结构(html): 1.1:页面结构: 1.2:标签类型: 1.2.1:块标签: 1.2.2:行内标签: 1.2.3:行内块标签: 1.2.4:块标签与行…...

MHA高可用-解决MySQL主从复制的单点问题
目录 一、MHA的介绍 1.什么是 MHA 2.MHA 的组成 2.1 MHA Node(数据节点) 2.2 MHA Manager(管理节点) 3.MHA 的特点 4. MHA工作原理总结如下: 二、搭建 MySQL MHA 实验环境 …...
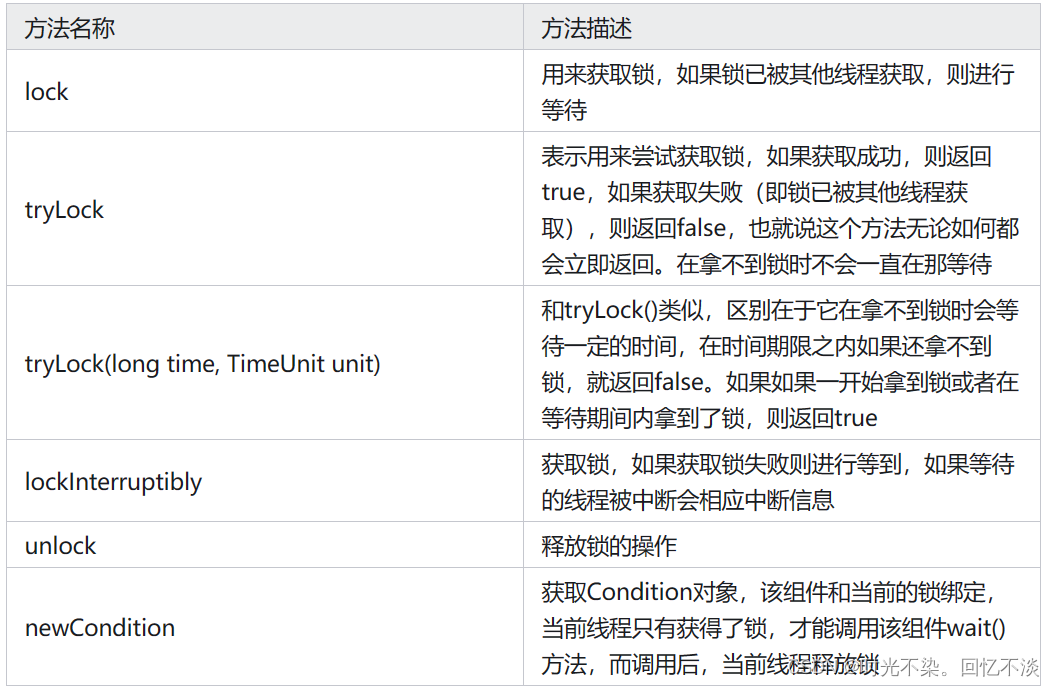
【多线程】震惊~这是我见过最详细的ReentrantLock的讲解
一.与synchronized相比ReentrantLock具有以下四个特点: 可中断:synchronized只能等待同步代码块执行结束,不可以中断,强行终断会抛出异常, 而reentrantlock可以调用线程的interrupt方法来中断等待,继续执行下面的代码。 在获取锁…...
分布式链路追踪与云原生可观测性
分布式链路追踪系统历史 Dapper, a Large-Scale Distributed Systems Tracing Infrastructure - Google Dapper,大规模分布式系统的跟踪系统大规模分布式系统的跟踪系统:Dapper设计给我们的启示 阿里巴巴鹰眼技术解密 - 周小帆京东云分布式链路追踪在金…...
CSS3新增的语法(三)【2D,3D,过渡,动画】
CSS3新增的语法(三)【2D,3D,过渡,动画】 10.2D变换10.1. 2D位移10.2. 2D缩放10.3. 2D旋转10.4. 2D扭曲(了解)10.5. 多重变换10.6. 变换原点 11. 3D变换11.1. 开启3D空间11.2. 设置景深11.3. 透视点位置11.4. 3D 位移11…...
Flutter应用在苹果商店上架前的准备工作与注意事项
引言 🚀 Flutter作为一种跨平台的移动应用程序开发框架,为开发者提供了便利,使他们能够通过单一的代码库构建出高性能、高保真度的应用程序,同时支持Android和iOS两个平台。然而,完成Flutter应用程序的开发只是第一步…...

如何开启MySQL的binlog日志
1.启用远程连接: 如果你想要允许远程主机连接到MySQL服务器,需要进行以下步骤: 确保MySQL服务器的防火墙允许远程连接的流量通过。在MySQL服务器上,编辑MySQL配置文件(一般是my.cnf),找到bind-…...
)
设计模式|状态机模式(State Machine Pattern)
文章目录 结构使用步骤示例使用状态机的场景常见面试题 状态机模式(State Machine Pattern)是一种用于描述对象的行为软件设计模式,属于行为型设计模式。在状态机模式中,对象的行为取决于其内部状态,并且在不同的状态下…...

Django源码之路由的本质(上)——逐步剖析底层执行流程
目录 1. 前言 2. 路由定义 3. 路由定义整体源码分析 3.1 partial实现path函数调用 3.2 图解_path函数 3.3 最终 4.URLPattern和Pattern的简单解析 5. 小结 1. 前言 在学习Django框架的时候,我们大多时候都只会使用如何去开发项目,对其实现流程并…...

基于深度学习的植物叶片病毒识别系统(网页版+YOLOv8/v7/v6/v5代码+训练数据集)
摘要:本文深入研究了基于YOLOv8/v7/v6/v5的植物叶片病毒识别系统,核心采用YOLOv8并整合了YOLOv7、YOLOv6、YOLOv5算法,进行性能指标对比;详述了国内外研究现状、数据集处理、算法原理、模型构建与训练代码,及基于Strea…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...
